一种基于神经网络的离散傅里叶矩阵重构方法研究

黄权，阮建高

（工业和信息化部电子第五研究所，广东广州 510610）

在近场扫描电磁图像的处理[1-3]中，需要对电磁图像进行变换，如空域变换、频域变换，近场扫描电磁图像通过电磁场探头探测得到[4-6]。传统的快速傅里叶变换能够对电磁图像进行快速运算后得到结果，但基于近场扫描电磁图像所反映的电磁辐射图案的多样性，希望能够设计一种算法去学习这些图案的特征，从而为电磁图案的后续分析如聚类等提供有效的图案特征，神经网络是最适合学习图案特征的框架，在研究的过程中发现神经网络不仅可以有效地学习到电磁图案的特征，还能够学习到离散傅里叶矩阵。

目前，深度学习的绝大多数构建模块、技术和架构都基于实数的运算和表征。但是，近来在循环神经网络和其他更古老的基础理论上的分析表明复数可以有更加丰富的表征能力，也可以促进对噪声鲁棒的记忆检索机制[7-9]。尽管它们在带来全新的神经架构上有引人注目的性质和潜力，但由于缺少设计这种模型所需的构建模块，复数值的深度神经网络一直处于边缘化的状态[10]。随着计算机硬件的发展，神经网络的应用越来越广泛，在预测、分类方面取得了很大的应用[11]，比如推荐系统、人脸识别等。

Reichert 等人从生物学的角度出发，将复数神经元用在深度神经网络中，这些使用复数表示的神经元具有更加丰富的表达能力，复数值的公式允许人们用神经元的放电率和活动的相对时间来表示神经元的输出。该复数神经元的振幅代表放电率，而其相位则代表活动的相对时间[12]。复数中的相位信息在信号处理时也是十分重要的，在语音信号中，相位信息影响着语音信号的可理解性[8]。Oppenheim 和Lim 还表明，在图像的相位中存在的信息量足以恢复以其大小编码的大部分信息。事实上，相位在编码形状、边缘和方向时提供了对象的详细描述[13]。

最近，Rippel等人将傅里叶谱表示用于卷积神经网络，提供一种在频谱域中参数化卷积核权值的技术，并在信号的频谱表示上执行池化[14]，然而，作者在论文中回避了执行复数值卷积，而是从空间域中的实值进行核卷积构建。为了确保谱域中的复数值参数化映射到实数值核函数，作者对谱域权重施加了共轭对称约束，这样当对它们应用傅里叶逆变换时，它只产生实数值的核函数[14]。

离散傅里叶变换作为一种有效的信号处理工具得到了广泛的应用，经典的快速傅里叶变换[15]更是将这个算法的应用发挥到了极致，但是快速傅里叶变换涉及到复数运算，而目前神经网络在复数运算方面基本上是不支持的，为了将神经网络应用到信号处理中，一方面设计可以进行复数运算的神经网络，另一方面是通过某种变换和设计，将复数进行拆解，使之能够按照实数进行计算，却不丢失原来复数运算包含的信息。

该文研究的离散傅里叶矩阵构建方法，完美地避开了复数运算，同时保留了和原始矩阵同样的信息量，并基于神经网络来学习和重构离散傅里叶矩阵，该矩阵可用于近场扫描之后的数据处理中[17]。

1 研究内容

1.1 离散傅里叶矩阵设计的数学原理

对于一个长度为N的信号序列x=[x0,x1,…,xN-1]，它的离散傅里叶变换公式为:

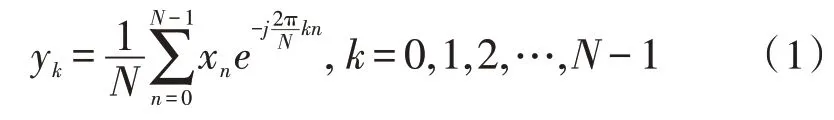
式（1）可以写成点积的形式：

式（2）写成矩阵形式：

式（3）写成矩阵形式：

其中，F∈RN×N,(F)kn=。式（2）、（3）都包含复数，复数运算是比较复杂和耗时的，因此引入欧拉公式:

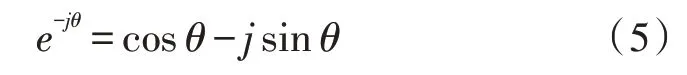
对此，令：

代入式（5）可得：

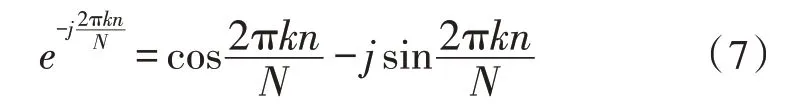
将式（7）的实部和虚部分开，然后排放在一个矩阵的上半部分和下半部分：

令WFourier表示式（8）右边的复指数值构成的矩阵，x表示[x0,x1,…,xN-1]T，则式（8）可以简写为：

y和包含的信息是完全一样的，但是式（9）不包含复数计算，因为引入欧拉公式将其实部和虚部放在矩阵的上半部分和下半部分，所以的长度是y长度的2倍。

1.2 神经网络设计

1.2.1 神经网络架构

如图1 所示，所设计的神经网络共有两层，输入层因为用于原始数据输入，通常只是进行了展平处理，对数据没有影响，所以不作为层计数，隐藏层的神经元数量为输入层神经元数量的2 倍，输出层只有一个神经元，用于计算损失。

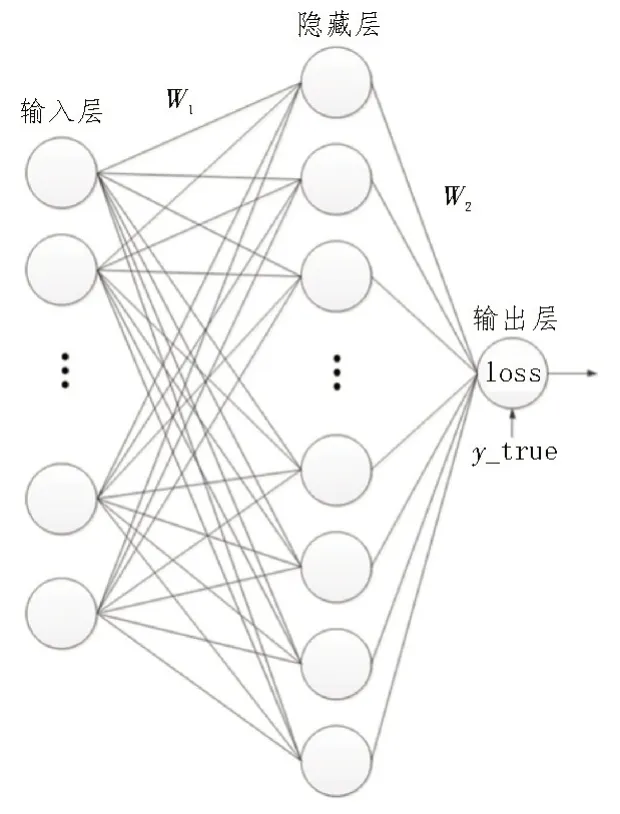
图1 神经网络结构设计

1.2.2 训练过程

如图2 所示是神经网络重构离散傅里叶矩阵的原理框图，重构步骤如下：

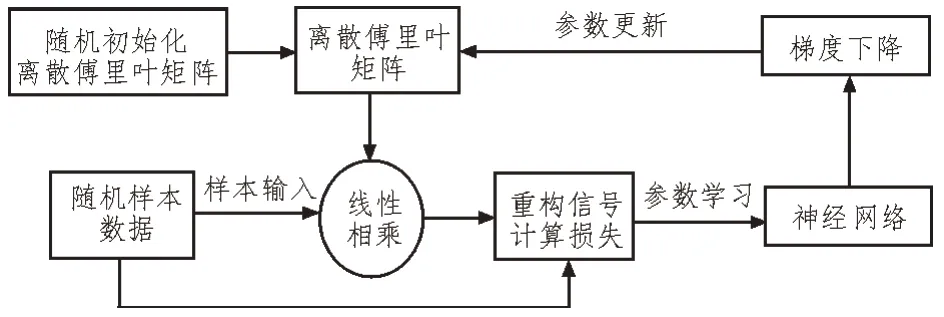
图2 神经网络训练的原理框图

1）随机初始化离散傅里叶矩阵WFourier，该矩阵是神经网络需要学习的参数；

2）生成随机样本输入x，与第1）步的参数矩阵进行线性相乘；

3）根据式（3）取出对应的实部和虚部，进行信号的重构，重构的方法如下：

已知一个信号的离散傅里叶变换的系数y=a+jb，其中y是一个复数，根据傅里叶分析理论，则对应的信号部分x为：

代入y=a+jb，展开可得：

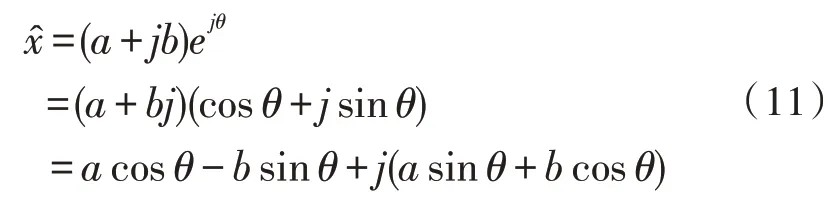
其中，a和b对应第3）步中实部和虚部。

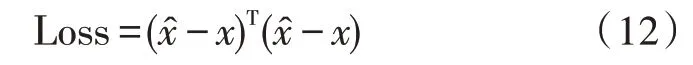
5）式（12）的损失函数（LossFunction）作为神经网络训练精度的衡量标准，并计算它的梯度后，进行参数更新，重复从第（1）步-第（4）步继续训练，直到训练达到指定的次数或者符合误差要求。

2 实验结果与分析

文中的实验环境为搭载Intel(R) Core(TM) i5-8265U CPU@1.60 GHz 1.80，双核1.60 GHz 主频处理器，内存8 GB的计算机，实验在64位Windows 10操作系统，使用神经网络框架pytorch 1.8.1+cpu 版及numpy1.16.5 条件下进行实现。

如图3 所示是理论计算的离散傅里叶矩阵与神经网络学习到的离散傅里叶矩阵的对比，其中神经网络迭代次数为10 000次，从图形上可以直观地看出，神经网络基本上学习到了离散傅里叶矩阵的特征。

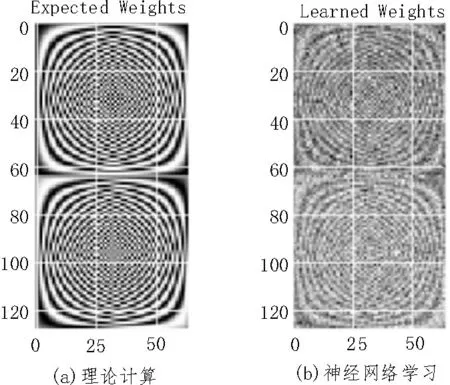
图3 两种方法得到的离散傅里叶矩阵的对比

如图4和图5所示，可以看出重构信号的损失值和RMSE在2 000次迭代以后基本上不变，即通过神经网络学习到的离散傅里叶矩阵已经能够很好地还原原始信号，同时也说明在精度上，神经网络学习到的离散傅里叶矩阵基本上不再随着迭代次数的增加而有所提升。

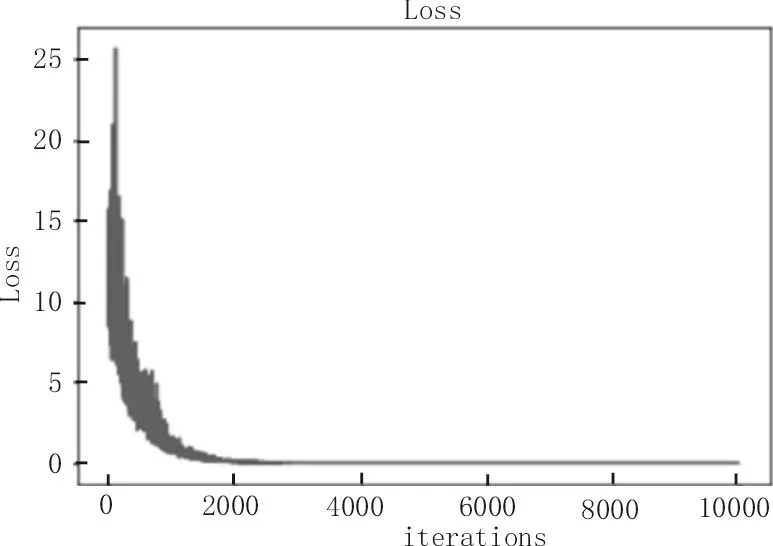
图4 重构信号的损失值随迭代的变化

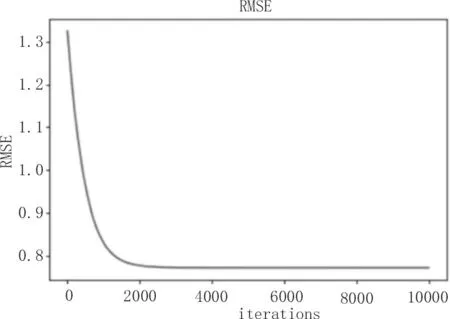
图5 离散傅里叶矩阵均方差随迭代的变化

图6 是原始的信号，图7 是使用神经网络学习的离散傅里叶矩阵重构的信号，可以看出，两种信号几乎完全相同，这是因为在神经网络训练2 000 次之后，神经网络学习到的离散傅里叶矩阵基本上与理论计算的离散傅里叶矩阵完全相同，这可以从图4和图5 得到验证。文中的实验数据没有加入噪声，因而重构信号的误差取决于神经网络学习到离散傅里叶矩阵的误差，从图5 中可以看出，这个误差在迭代2 000 次之后基本上再无变化，假如数据包含噪声，那么这种情况可能是神经网络在训练时过拟合了，因为从图3 来看神经网络学习到的离散傅里叶矩阵和理论计算的离散傅里叶矩阵是有差别的，而迭代次数在2 000 次之后对这种差别却无明显的改善，说明神经网络在结构分布上可以完美地学习到离散傅里叶矩阵，但是在数值精度上不能完美地接近。通过实验得到迭代次数与模型损失关系如表1 所示。

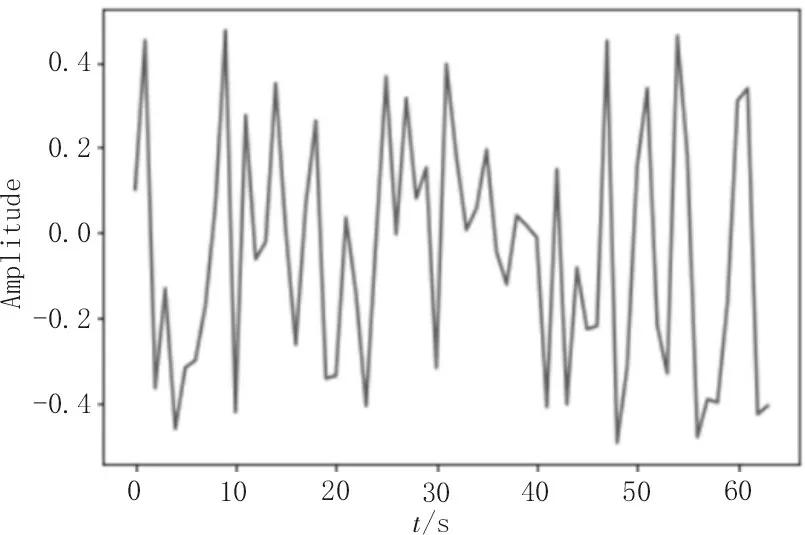
图6 原始信号

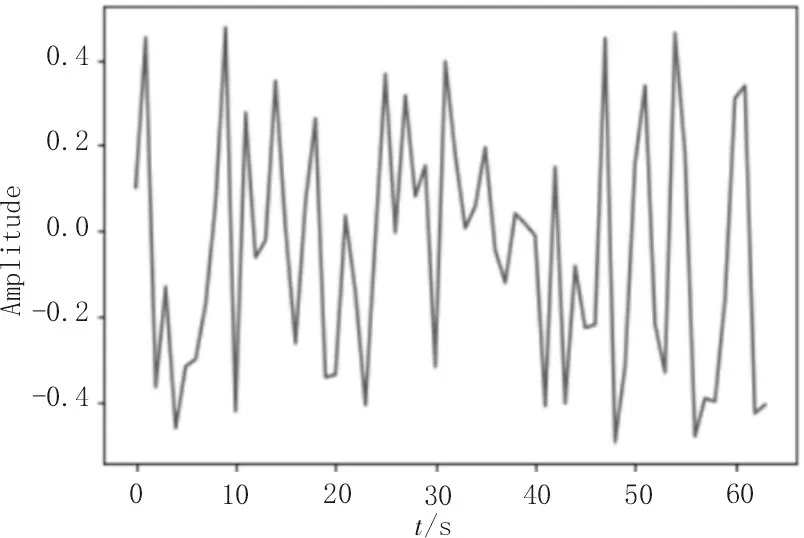
图7 神经网络学习的离散傅里叶矩阵重构的信号

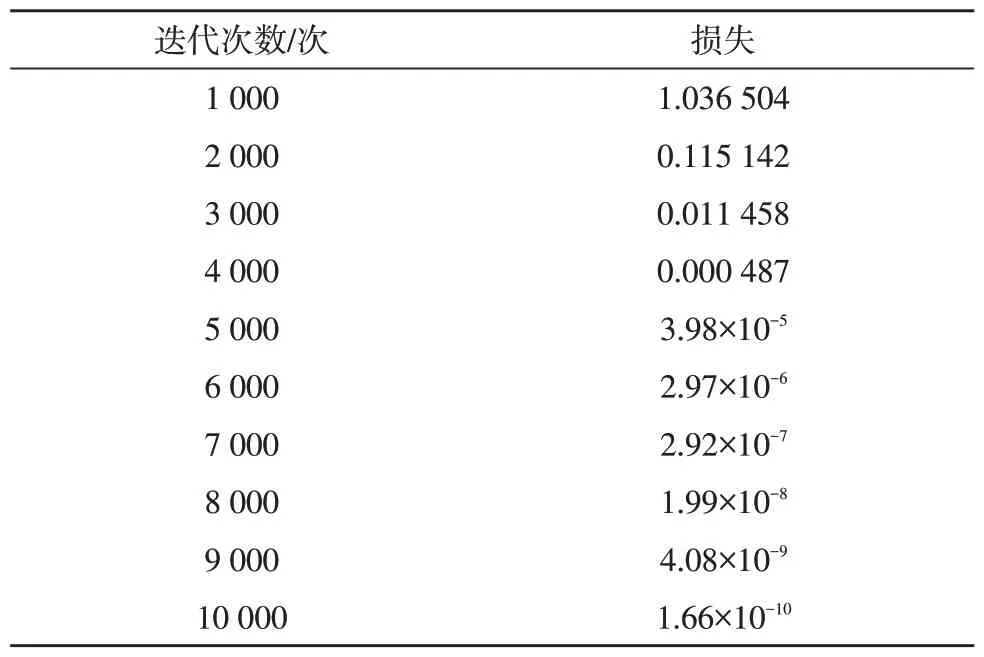
表1 迭代次数与模型损失

通过表1可以看出，迭代次数在4 000 次以后，损失值基本上接近于0。

3 结论

该文提出了一种将离散傅里叶变换避开矩阵运算的复数操作方法，并使用神经网络来学习该矩阵。可以看出神经网络很完美地学习到了该矩阵，且用该矩阵重构的信号与原始信号基本相似。其根本原因是该文设计的神经网络是一种线性变换，而离散傅里叶变换也是一种线性变换。那么在使用随机梯度下降的迭代中，只要迭代次数足够，就可以完美地学习这种线性变换。后续可研究的工作是用神经网络研究二维离散傅里叶变换，同时结合图像降噪的理论研究近场扫描电磁数据的降噪设计。