非相似圆筒内爆膨胀模型设计及试验验证

沈 飞，王 辉，罗一鸣，余文力，王煊军

(1.火箭军工程大学，陕西 西安 710025；2.西安近代化学研究所，陕西 西安 710065)

引 言

圆筒试验是表征炸药作功能力的重要试验方法，圆筒试验可选择不同尺寸的试样，但试样结构一般遵循同一相似准则[1]，这种相似性结构使炸药爆轰转换的各类能量之间的比值近乎一致，便于不同尺寸圆筒试验所获各物理量值之间进行对比，所不同的是，圆筒的有效膨胀时间与其尺寸近乎成正比[2]。因此，反应时间较长的炸药需要采用大尺寸圆筒试样表征[2-3]。然而，根据该相似准则，圆筒尺寸增加一倍时，圆筒的有效膨胀时间仅增加一倍左右，但药量提升约8倍，造成试验成本及安全风险大幅增加。若仅增加圆筒的壁厚，降低圆筒试样的装填比，则圆筒膨胀速度将显著降低，从而可延迟圆筒的破裂时间；此外，再适当延长圆筒的长度，延迟两端稀疏波到达测试位置的时间，则可增加含铝炸药在圆筒内的有效释能时间。然而，这种与标准圆筒不相似的结构必然会改变圆筒动能、变形能、爆轰产物动能等物理量之间的比例关系，那么在计算炸药爆轰所转换的动能时，传统的格尼模型对计算精度的影响需要深入分析。对于该问题，国外研究人员[1-3]针对“半壁厚”(圆筒的厚壁为其内径的0.05倍)圆筒结构与标准圆筒结构的试验数据进行了大量对比，发现基于传统格尼能的计算模型，“半壁厚”圆筒结构所获得的炸药格尼能高于标准圆筒，但未给出相应的修正模型。SINGHA等[4]以类似思想设计了不同壁厚、不同材料的圆筒结构，并用于各类非理想炸药的爆炸驱动性能研究，但主要关注其壳体的断裂特性以及爆轰驱动的能量利用率等问题，未关注非相似圆筒的格尼能计算精度。

鉴于此，本研究针对这种仅增加壁厚的非相似圆筒试样在内爆条件下的膨胀过程进行理论分析，重点考虑厚壁圆筒变形能、爆轰产物动能的计算过程，建立适用于非相似圆筒试样的炸药格尼能计算模型。然后基于TNT炸药格尼能较为稳定、不随驱动释能时间的延长而发生显著变化的特点，将3个不同壁厚圆筒试样均装填相同密度的TNT炸药，通过分析其试验图像及残片来研究试验的可行性，并对比3个试样所获得的格尼能曲线，验证计算模型的准确性，以期能够为释能时间较长的含铝炸药提供一种低成本、低安全风险的圆筒试验途径。

1 圆筒膨胀过程的动力学模型

1.1 圆筒的动能

在内部炸药稳态滑移爆轰加载下，圆筒膨胀速度、偏转角、炸药爆速之间存在如图1所示的几何关系[3]。

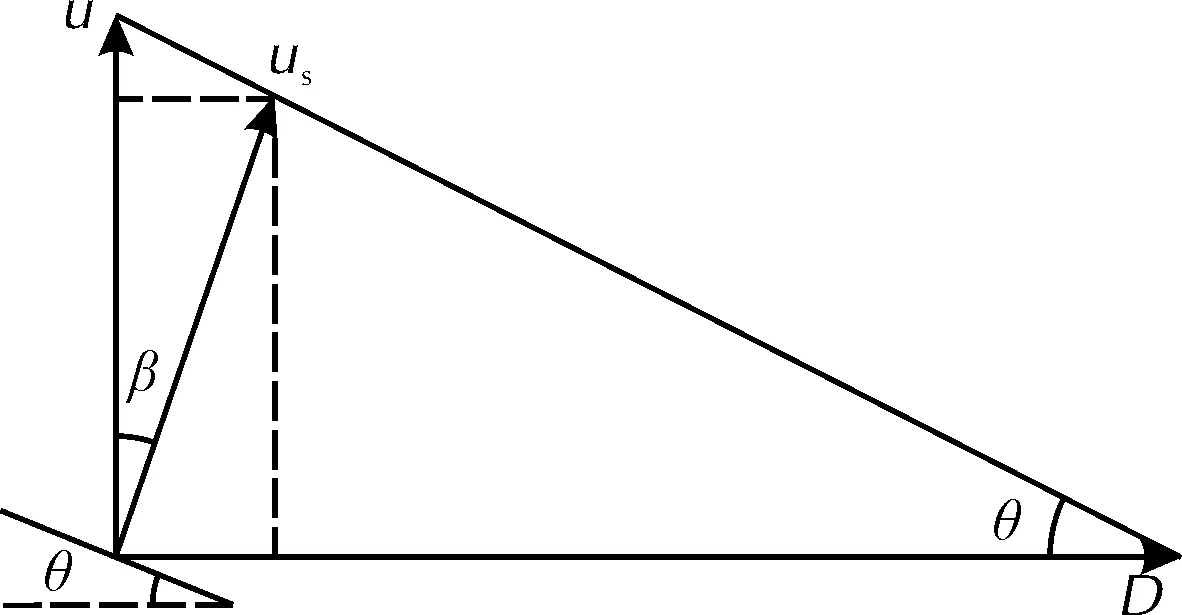
图1 圆筒膨胀速度与偏转角关系示意图Fig.1 Schematic diagram of relationship between expansion speed and deflection angle of cylinder wall

图1中，u为从圆筒径向观测的相速度；us为圆筒的质点速度；θ为圆筒膨胀时的偏转角；β为us与u之间的夹角；D为炸药爆速。各物理量间存在如下关系：

β=θ/2=arctan(u/D)/2

(1)

(2)

由于圆筒内外表面处的物理量有一定差异，因此，采用下标“i、e、m”分别表示圆筒的内表面、外表面、质量中心面的各物理量。圆筒的半径采用r表示，且u=dr/dt；采用下标“0”表示各位置半径的初始值。试验时，可采用激光干涉法直接测量圆筒外表面的速度ue，也可采用狭缝扫描法测量圆筒外表面的径向膨胀距离(re-re0)，最终都可基于圆筒横截面积不变的假定获得圆筒质量中心面的径向速度um[5-6]。然后根据式(1)和式(2)可计算出um所对应的质点速度usm，假定圆筒同一横截面处的各点速度相同，则可计算出圆筒的动能。

上述计算过程对于不同壁厚的圆筒试样一般均适用，且可由式(3)计算出单位质量炸药爆炸产生的圆筒动能Ec[7]：

(3)

式中：ρCu和ρHE分别为铜和炸药的密度。而分析炸药爆炸产生的全部动能时，还需要考虑爆轰产物动能、圆筒变形能等。对于满足相似标准的圆筒试样，考虑到圆筒变形能等占总爆炸能的比值小，一般仅考虑圆筒和炸药爆轰产物的动能，且不考虑爆轰产物沿轴向的膨胀速度，仅假设其径向膨胀速度沿半径呈线性分布，则单位质量炸药爆轰产物动能Ep的表达式为[7]：

(4)

则炸药格尼能Eg可表示为：

Eg=Ec+Ep

(5)

当圆筒壁厚与内径的比值增加时，试样的装填比减小，则圆筒的变形能占爆炸总能量的比值将提升，若将其忽略，则可能显著低估炸药转换的动能；且铜管径向速度的降低会增加对爆轰产物的径向约束，导致其流动方向可能会发生变化，计算其动能时需要采用更为精确的计算方法。

1.2 圆筒的变形能

假定圆筒在爆轰驱动下的膨胀过程仅发生平面应变，则其径向应变εr为[8]：

(6)

再结合Von Mises屈服准则[9]，则可获得单位长度铜管的塑性变形功W为：

(7)

式中：Ys为无氧铜的动态屈服强度，取235MPa[10]。根据式(7)，可计算出单位质量炸药爆炸产生的圆筒变形能W*为：

(8)

1.3 圆筒膨胀的驱动力

圆筒膨胀过程主要需要考虑其径向运动，结合图1所示的各物理量关系及式(2)，并以圆筒质量中心面的加速过程代表对应的圆筒截面，则由动量定理可建立其径向运动方程，即：

(9)

由式(7)，并结合圆筒横截面积保持不变的假定，即有redre=ridri，可得：

(10)

将式(7)和式(1)代入式(9)，可获得圆筒内爆轰产物压力p的表达式，即：

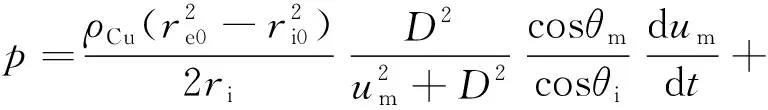
(11)

获得圆筒膨胀位移及速度的测量值后，可根据圆筒横截面积保持不变的假定，获得圆筒同一截面其他位置的位移和速度值，将其代入式(11)和式(1)，则可计算出相应时刻的爆轰产物压力，为爆轰产物流场的计算提供输入。

2 爆轰产物的动力学模型

在圆筒结构中，爆轰产物的流动受到爆轰波形、炸药驱动能力、装填比等多个因素的影响，且随着圆筒的膨胀，其流动方向发生改变。为了尽可能地简化其计算模型，采用以爆轰波阵面为基准的动态相对坐标系进行分析，图2为其示意图，并假定在同一圆截面，爆轰产物的相对速度值均为vp，且爆轰产物流线的偏转角θp=arctan(r/ri·tanθi)[11]。

图2 爆轰产物的流动受力示意图Fig.2 Schematic diagram of flow and force of detonation products

则爆轰产物相对速度沿轴向的分量vap为：

(12)

在波阵面两侧，炸药和爆轰产物满足质量、动量守恒关系。

质量守恒：

(13)

动量守恒：

(14)

式中：ρp为爆轰产物的密度。式(14)右侧第三项表示产物压力对圆筒轴向运动的作用，考虑到动态坐标x≈Dt关系，则可变为：

(15)

将式(13)代入式(15)，可得出：

(16)

此外，由式(13)可获得爆轰产物相对比容V的表达式为：

(17)

(18)

将式(17)代入式(18)，则有：

(19)

从而可计算出爆轰产物的实际相对比容、压力、动能等参数。

对于非相似结构的圆筒试样，计算其内部炸药爆炸产生的格尼能时，若考虑圆筒动能及变形能、爆轰产物沿轴向和径向的运动，则其计算公式为：

Eg=Ec+W*+Ep

(20)

式中：Ec、W*、Ep的表达式分别如式(3)、式(8)、式(19)所示，且具体计算时，可编制相应的计算程序。

3 不同结构的圆筒试验

3.1 样品及试验过程

试验选取标准型Φ50mm圆筒试样(试样1)及两种内径均为Φ50mm的非相似圆筒试样，具体尺寸列于表1，其中，试样2和试样3的壁厚分别为试样1的1.5倍和2倍。这3种圆筒均采用TU1无氧铜加工，内部装填密度为1.58g/cm3的TNT压装药柱。此外，经仿真预估，内部炸药爆轰产物膨胀至相同比容时，试样2和试样3所需时间分别约为试样1的1.2倍和1.4倍，根据稀疏波的传播特点，则将这两种试样的长度分别延长至试样1的1.2倍和1.4倍，以避免其膨胀过程中，内部爆轰产物过早受到两端稀疏波的影响。

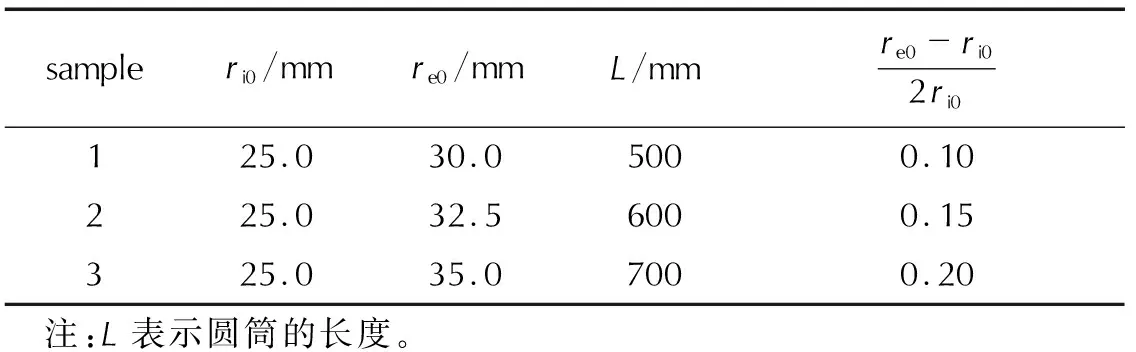
表1 圆筒试样的尺寸Table 1 Size of cylinders

试验采用GSJ扫描式高速转镜相机记录圆筒的膨胀过程，将距离圆筒尾部约为总长度0.4倍处的圆截面作为扫描测量位置，相机扫描速度设定为1.5mm/μs，并采用氩气弹进行背景照明；采用电探针粘接在试样两端的药柱端面，以获取TNT在圆筒内的平均爆速。具体试验布局可参考文献[6]。

3.2 圆筒的断裂特性分析

试验所获底片如图3所示。

图3 圆筒试验获得的图像Fig.3 Images obtained from the cylinder test

通过对图3所示图像中的黑白分界线进行数字化判读，可获得圆筒外表面的径向位移随时间的变化历程，即(re-re0)—t曲线。其中，图像横坐标与相机扫描速度的比值即为时间值，纵坐标则对应圆筒外表面的径向位移。

然而，在数据处理之前，还需要判断试验数据的有效性，即判断圆筒是否发生了早裂而造成产物溢出。对于标准圆筒，要求其发生贯穿性破裂前，其最大膨胀位移不小于圆筒初始内径，以确保此时爆轰产物的相对比容V不小于10。在分析圆筒破裂前的最大膨胀位移时，可从图像黑白边界的光滑性及圆筒残片两方面进行。由于溢出的爆轰产物自身也具有发光特性，会造成试验图像的边界线出现突跃，尤其是在圆筒膨胀初期和中期，溢出的产物具有较高的速度，这一突跃现象较为明显。图3中各图像的黑白分界线均较为光滑，因此，可以判定这3种圆筒试样在膨胀初期和中期发生破裂的可能性较小。

结合圆筒横截面积保持不变的假定，可根据试验后的圆筒残片尺寸计算出圆筒破裂前的最大膨胀位移，试样1和试样3的残片如图4所示。

图4 试验后回收的圆筒残片Fig.4 The fragments collected after the test

由图4(a)可知，试样1的残片大多为长条形，长度约为20～60mm，宽度约为5～10mm，大多数破片的长宽比相近，厚度约为1.0～1.5mm；由图4(b)可知，试样3的残片形状差异较大，长条形较少，大部分残片的长度约为20～40mm，宽度约为10～15mm，厚度约为2.6～3.1mm，而少数长条形残片的长度超过100mm。试样1的初始壁厚为5mm，残片厚度的最大值为1.5mm，则可计算出圆筒破裂前，re-re0的最大值约为62.4mm；试样3的初始壁厚为10mm，残片厚度的最大值为3.1mm，则圆筒破裂前re-re0的最大值约为63.3mm。这一方面表明壁厚增加一倍后，圆筒破裂前的最大位移也能满足试验的基本要求，该测量结果是有效的；另一方面也反映出仅增加圆筒的壁厚时，圆筒的破裂时间虽然显著延迟，但破裂前的最大膨胀位移并没有增加，难以用于表征炸药爆轰产物进一步膨胀时的释能特征。这可能是由于非相似圆筒结构与标准圆筒的断裂过程差异较大所导致。圆筒残片的断裂面外形如图5所示。

图5 圆筒残片的断裂面外形Fig.5 The shape of the fracture surface of the fragment

由图5可以看出，标准圆筒(试样1)的残片断面较薄，主要是发生拉伸断裂；而壁厚增加一倍的试样3，其残片的断面较为复杂，反映出其发生了拉伸、剪切、撕裂等多个作用过程。

3.3 圆筒膨胀位移及速度

采用式(21)将试验所获的(re-re0)数据转换为(rm-rm0)—t数据：

(21)

(22)

式中：aj、bj、t0均为拟合参数，具体数值列于表2。

表2 装填TNT的圆筒膨胀位移曲线拟合参数Table 2 Fitting parameters of expansion displacement curves of cylinders filled with TNT

将表2中拟合参数值代入式(23)可计算出圆筒的径向膨胀速度um：

(23)

基于这3种圆筒试样的膨胀位移和速度曲线，可按照本研究中的计算流程获得爆轰产物及圆筒的其他动力学物理量的数值。其中，爆轰产物相对比容V随时间的变化关系需要首先关注，这是设计非相似圆筒的基本出发点。结合式(17)计算出的这3种试样的V—t曲线如图6所示。

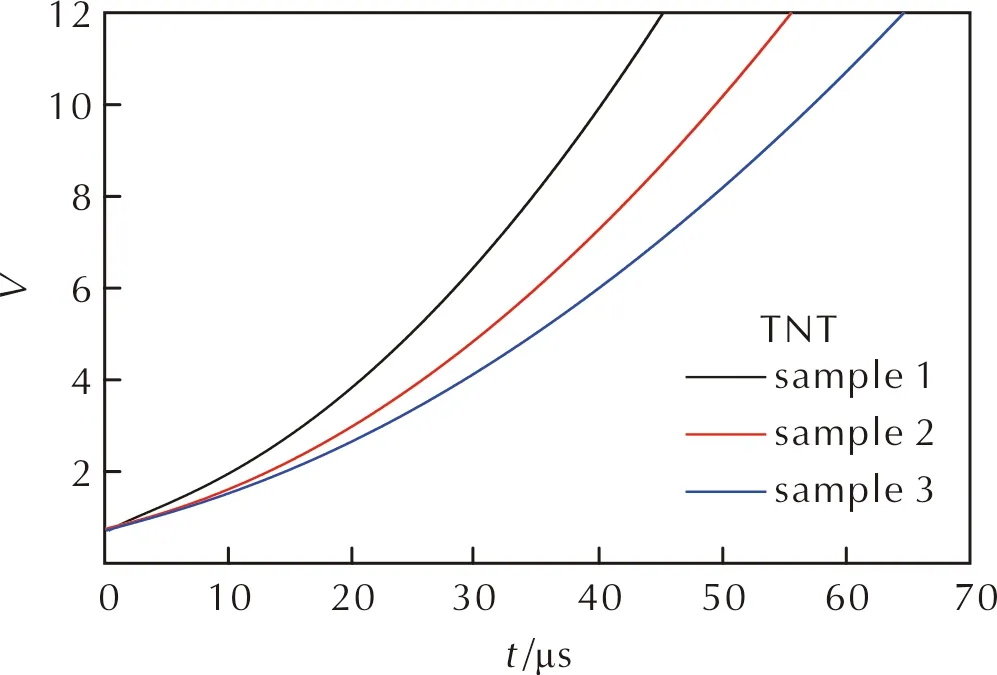
图6 爆轰产物的V—t曲线Fig.6 V—t curves of detonation products

由图6可以看出，爆轰产物膨胀至相同比容时，厚壁圆筒所需要的时间较标准圆筒(试样1)明显延长。以产物膨胀至V=10的状态为例，试样1仅需40.2μs，试样2和试样3所需时间则分别增加了23%和42%。若采用结构相似型标准圆筒，根据其有效膨胀时间与其尺寸成正比的特点可知，其内径须达到Φ70mm，才能使其有效膨胀时间与样品3相当，而装药量须增至样品1的2.7倍，相比而言，样品3的装药量仅为样品1的1.4倍。然而，壁厚的增加也减小了圆筒的膨胀速度，圆筒试样的usm—V曲线如图7所示。

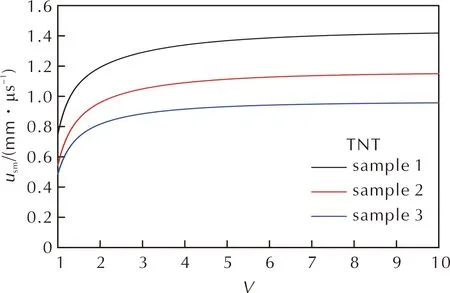
图7 圆筒试样的usm—V曲线Fig.7 usm—V curves of the cylinder samples

由图7可以看出，这3种试样膨胀速度的增长过程相似，厚壁圆筒虽然时间增长了，但其膨胀速度曲线没有显示出继续增长的趋势。这说明虽然TNT炸药在爆炸过程中存在一定的二次反应特性，但其爆炸驱动能量比较稳定。当爆轰产物膨胀至V=7时，圆筒膨胀速度基本达到了最大值，其中，试样1的usm值约为1.4mm/μs，而试样2和试样3分别为其81.1%和67.7%。

3.4 炸药的格尼能及组成

爆轰产物膨胀过程中产生的能量主要由壳体动能、爆轰产物动能、壳体变形能组成，圆筒壁厚增大后，对爆轰产物的约束加强，这3部分能量的比例会发生改变，下面采用本研究中的计算方法进行分析。圆筒动能的计算仍采用式(3)计算，其结果如图8(a)所示。由图8(a)可以看出，随着圆筒壁厚增加，虽然其膨胀速度显著下降，但单位质量炸药爆炸产生的圆筒动能略有增加，当V=10时，试样2和试样3的动能较试样1分别提升3.1%和4.7%。由式(7)和式(8)可计算出3种试样的圆筒变形能，其结果如图8(b)所示。由图8(b)可以看出，当V相同时，圆筒变形能与圆筒的质量近似成正比，当V=10时，单位质量炸药爆炸产生的圆筒变形能从试样1的0.078kJ/g增至试样3的0.161kJ/g，这使得厚壁圆筒的变形能不宜忽略。

图8 圆筒动能和变形能随爆轰产物相对比容变化的曲线Fig.8 The curves of kinetic energy and strain energy of cylinders with the relative specific capacity of detonation products

由于圆筒壁厚增大使爆轰产物的流动发生较大变化，因此，其动能的变化需要重点关注。本研究中采用的模型考虑了爆轰产物沿轴向的膨胀速度，图9显示了由式(19)和式(4)分别计算的结果。

图9 爆轰产物动能随相对比容变化的曲线Fig.9 The curves of the Kinetic energy of detonation products with the relative specific volume

从图9中可以看出，随着圆筒壁厚的增加，爆轰产物动能降低；式(19)的计算结果明显高于式(4)，其中，当V=10时，对于试样1，式(19)的计算值较式(4)提高25.4%，而对于试样2和试样3，则该比例分别提高至46.2%和75.4%，这表明圆筒内径相同时，其壁厚越大，爆轰产物沿轴向的膨胀速度越需要考虑。此外，采用式(19)还获得了爆轰波阵面过后，爆轰产物轴向速度迅速降低的过程，但考虑到圆筒试验数据在膨胀曲线初期的精度问题，对该部分的计算值不做深入量化分析。

炸药的格尼能是本试验最关注的结果，图10显示了式(5)和式(20)计算出的3种试样的格尼能。

从图10中可以看出，采用式(5)计算时，3种试样的格尼能曲线差异显著，壁厚越大，则数值越低；而采用式(20)计算时，3种试样的格尼能曲线基本吻合。这表明，本研究中的计算模型可以更准确地评估非相似圆筒中的炸药驱动性能。

4 结 论

(1)对于内径为Φ50mm的非相似圆筒试样，当其壁厚增加后，由于其断裂过程较标准圆筒更为复杂，导致破裂前的最大位移并未显著增加，但仍能确保爆轰产物的相对比容不小于10，满足圆筒试验的基本要求。

(2)爆轰产物膨胀至相同比容时，圆筒变形能与圆筒的质量近似成正比，当仅增加圆筒壁厚时，其变形能不宜忽略，且爆轰产物轴向运动的能量占其总动能的比例提升，计算模型须考虑爆轰产物的轴向流动。

(3)采用本研究优化后的格尼能计算模型所获得的3种不同壁厚圆筒试样的格尼能变化曲线基本吻合，可以更准确地评估非相似圆筒中的炸药驱动性能。

(4)内径Φ50mm、壁厚10mm、长度700mm的非相似圆筒结构，能够使爆轰产物的有效膨胀时间较Φ50mm标准圆筒提升42%，而装药量仅增加40%，不仅满足释能时间较长的含铝炸药的试验需求，而且能显著降低试验成本及安全风险。