EGM2008 模型GNSS 高程转换在山区地形图测量的研究
刘政纲,梁迎春*
(1. 湖北省国土测绘院,湖北 武汉 430010)
随着测量技术的发展,GNSS 测量得到的点位具有厘米级甚至毫米级的坐标数据,但GNSS 技术测量得到的是大地高,而我国高程系统采用的是正常高,GNSS 高程不能直接应用于工程项目。正常高测量方法主要是水准测量和三角高程测量,测量程序繁杂,成本高、效率低,在地形复杂和大面积区域的测区费时费力,正常高测量成为影响项目进度的关键[1-2]。将GNSS 技术测得的大地高转换为工程项目使用的正常高,长期以来都是测量技术人员探索研究的热点。
1 EGM2008重力场模型
EGM2008重力场模型是2008年4月,由美国国家地理空间情报局(NGA)研制并推出的新一代地球重力场模型,模型的阶次至2 159 次(另外球谐系数的阶数已经扩展至2 190次),相当于模型的空间分辨率约为5′ (约9 km)。该模型采用了GRACE卫星跟踪数据、卫星测高数据和地面重力数据等,地面数据覆盖率达83.8%,部分重力数据空白区主要集中在南极,用卫星重力数据补充,是目前世界上拥有最高分辨率和精度的重力场模型[3]。
高程异常值求取通常采用GNSS 高程拟合,需要一定数量,分布均匀,且能覆盖整个拟合区域的GNSS水准点(同时具有大地高和正常高),通过模型拟合的方法求解高程异常值。此方法虽然对传统高程测量方式进行了改善,但需要在GNSS 点中联测较多的水准点,这些水准点还需均匀分布,有效覆盖整个拟合区域,工作量较大,并且在水准点较少时不能进行高程拟合。EGM2008 模型可以根据GNSS 测得准确的经纬度坐标(B、L),直接计算出该点的高程异常ζ,使得高程异常求取变得非常方便。EGM2008 模型高程异常在国内的总体精度为20 cm,华东华中地区为12 cm,华北地区为9 cm,西部地区为24 cm[3]。EGM2008模型在地形平缓的平原地区求解的高程异常精度优于地形起伏大的山区[4]。EGM2008 模型高程异常计算公式如下:

式中,ζ为高程异常值;GM 为地心引力常数;r为向径;γˉ为重力异常值;a为参考椭球长半径;b为点的纬度;L为点的经度;Cˉnm、Sˉnm为完全格式化扰动位系数;Pˉnmcosb为完全规格化的Legendre 函数;n为EGM2008最高展开阶数。
2 GNSS高程转换的原理与方法
GNSS 测量数据高程系统为大地高,我国高程系统采用的是正常高系统,正常高计算公式如下:

式中,h为正常高;H为大地高;ζ为高程异常。
似大地水准面指从地面点沿正常重力线量取正常高所得端点构成的封闭曲面。似大地水准面严格说不是水准面,但接近于水准面,只是用于计算的辅助面。各国似大地水准面都是在局部区域与大地水准面最为接近的面,EGM2008模型采用的似大地水准面与我国所采用的似大地水准面之间存在一个差值,即国家高程基准与EGM2008模型定义的全球高程基准之间的差值,考虑到这一差值,正常高计算公式如下:

式中,ζ为EGM2008模型计算的高程异常值;Δζ为模型差即EGM2008似大地水准面与我国采用的似大地水准面之间的差值。
由式(3)变化可得:

式中,Δζ可以通过拟合模型计算求得,拟合常用的模型有常数模型、平面模型、曲面模型。其中常数模型需要1 个以上的公共高程点,平面模型需要3 个以上的公共高程点,曲面模型需要6 个以上的公共高程点。
常数模型公式如下:

式中,Hi、hi、ζi分别为i点的大地高、正常高、EGM2008模型计算的高程异常值;n为公共高程点个数。
平面模型公式如下:

曲面模型公式如下:

式中,a0、a1、a2、a3、a4、a5为未知数;B为纬度;L为经度。
3 工程实例及精度分析
3.1 工程概况
某高速公路项目全长68 km,项目区平均高程1 500 m左右,相对高差600多米,需要完成1∶2 000比例尺像控点测量和地形图测量工作。通过资料收集,收集到4 个高等级水准点,分别为YZ01、YZ02、YZ03、YZ04。项目区每隔5 km 布设1 对GNSS 四等点,30个点均联测四等水准,具有正常高。在像控点测量过程中,对4个高等级水准点和30个四等水准点按照像控点的精度进行测量,获得经纬度坐标和大地高,利用EGM2008模型计算出各点的高程异常。通过公共点采用常数模型、平面模型、曲面模型3 种模型拟合计算出Δζ,求得各点拟合正常高。检核点的拟合正常高与水准正常高差值,分别进行精度分析,选取最佳的拟合模型,探索用少量水准点,作为拟合像控点正常高的方法。为了保证各种方案拟合结果精度分析可比性,下文16 种方案采用的GNSS 数据和水准数据均为同一套数据,方案结果不受GNSS 的测量精度、水准测量精度的影响。
3.2 常数模型与精度分析
根据公共点个数不同,常数模型拟合制定8 种方案,利用EGM2008 模型计算出像控点和34 个已知GNSS 水准点的高程异常,再通过常数模型拟合计算出Δζ,求取所有点的拟合正常高。公共点以外其余GNSS 水准点作为检核点,对拟合正常高与水准正常高差值进行统计,检核点精度统计表见表1。

表1 检核点精度统计表/m
方案1:1个公共点YZ01,位于项目起点;
方案2:1个公共点YZ04,位于项目终点;
方案3:1个公共点YZ03,位于项目内部;
方案4:2个公共点(YZ01、YZ04);
方案5:2个公共点(YZ02、YZ03);
方案6:2个公共点(YZ03、YZ04);
方案7:3个公共点(YZ01、YZ03、YZ04);
方案8:4个公共点(YZ01、YZ02、YZ03、YZ04)。
通过表1可知,方案1~8的高程中误差均小于0.2 m,满足《公路勘测规范细则》规定的像控点高程测量,其高程中误差不应超过基本等高距1/10 的要求(1∶2 000 航测地形图为0.2 m),基于EGM2008 模型采用常数模型拟合方法可实现GNSS 大地高转化为正常高,满足项目像控点高程测量精度的要求。GNSS高程转换的精度与距离已知公共高程点无显著关系,且转换精度与已知公共高程点个数无显著关系。
3.3 平面模型与精度分析
根据公共点个数不同,平面模型拟合制定如下5种方案,通过平面模型拟合计算出Δζ,求取所有点的拟合正常高,检核点精度统计表见表2。

表2 检核点精度统计表/m
方案9:3个公共点(YZ01、YZ03、YZ04);
方案10:4个公共点(YZ01、YZ02、YZ03、YZ04);
方案11:6个公共点(YZ01、D06、YZ02、YZ03、D28、YZ04);
方案12:7 个公共点(YZ01、D06、YZ02、D18、YZ03、D28、YZ04);
方案13:10 个公共点(YZ01、D03、D06、D09、YZ02、D18、YZ03、D28、D30、YZ04)。
通过表2 可知,方案9~13 的高程中误差均小于0.2 m,满足项目像控点高程测量精度的要求。基于EGM2008 模型采用平面模型拟合方法,GNSS 高程转换的精度随已知公共高程点个数增加精度有所提升。
3.4 曲面模型与精度分析
根据公共点个数不同,曲面模型拟合制定3 种方案,通过曲面模型拟合计算出Δζ,求取所有点的拟合正常高,检核点精度统计表见表3。

表3 检核点精度统计表/m
方案14:6个公共点(YZ01、D06、YZ02、YZ03、D28、YZ04);
方案15:7 个公共点(YZ01、D06、YZ02、D18、YZ03、D28、YZ04);
方案16:10 个公共点(YZ01、D03、D06、D09、YZ02、D18、YZ03、D28、D30、YZ04)。
通过表3 可知,方案14 的高程中误差大于0.2 m,不能满足项目像控点高程测量精度的要求。方案15、16 的高程中误差均小于0.2 m,满足项目像控点高程测量精度的要求。曲面模型拟合需要多余公共点,否则拟合精度较差,且GNSS 高程转换的精度随已知公共高程点个数增加精度无显著变化。
3.5 相同公共点不同模型精度对比
当公共点相同时,分别采用常数模型和平面模型拟合,对检核点拟合正常高与水准正常高差值进行统计。采用3 个公共点拟合后检核点误差分布如图1 所示,采用4 个公共点拟合后检核点误差分布如图2所示。

图1 3个公共点拟合后检核点误差分布图

图2 4个公共点拟合后检核点误差分布图
通过图1、2 可知,当公共点只有3~4 个时,常数模型、平面模型拟合精度都可以满足项目像控点高程测量精度要求,常数模型精度略高于平面模型。
当公共点相同时,分别采用平面模型和曲面模型拟合,对检核点拟合正常高与水准正常高差值进行统计。采用7 个公共点拟合后检核点误差分布如图3 所示,采用10 个公共点拟合后检核点误差分布如图4所示。
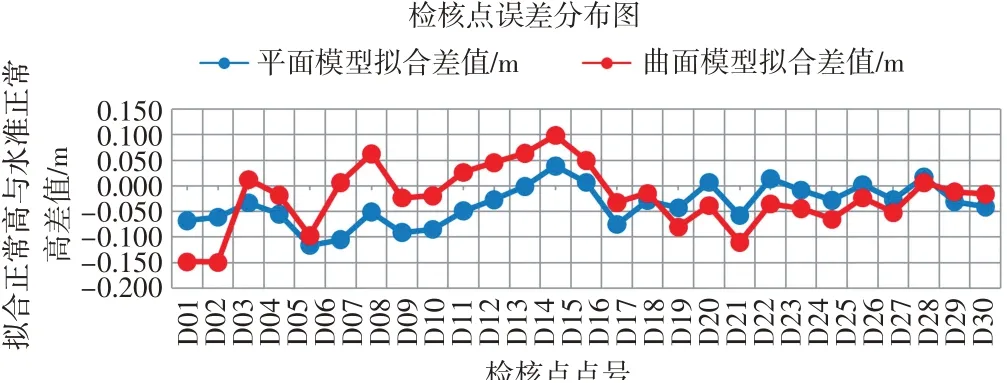
图3 7个公共点拟合后检核点误差分布图

图4 10个公共点拟合后检核点误差分布图
通过图3、4 可知,当只有7~10 个公共点时,平面模型、曲面模型拟合精度都可以满足项目像控点高程测量精度要求,平面模型精度略高于曲面模型。
项目本着既满足像控点正常高精度要求,又不使用GNSS 四等点的原则,采用YZ01、YZ02、YZ03、YZ04 作为公共点,通过常数模型拟合方法获得像控点正常高。
3.6 1∶2 000地形图高程精度检测
为了检核基于EGM 2008模型GNSS高程转换的像控点所成1∶2 000地形图高程精度,在联测了四等水准的控制点上架设基站,使用GPS-RTK和全站仪测量方法对1∶2 000地形图明显高程点进行测量,实测高程点1 848 个,实测高程点与地形图上点的高程精度统计见表4。

表4 高程精度统计表/m
通过表4可知,高程中误差为0.731 m,小于《公路勘测规范细则》规定的不应大于2 m 的要求,地形图高程精度满足要求。
4 结 语
本项目基于EGM2008 模型,通过采用常数模型、平面模型、曲面模型进行高程拟合求得正常高数据,与水准测量正常高数据进行比较,根据项目实践结果总结出一些经验:
1)在长度70 km的测区内,仅有1个已知水准点的情况下,基于EGM2008模型进行高程拟合可以获得较高精度的正常高数据。
2)基于EGM2008 模型进行高程拟合求得的正常高数据精度均匀,与距离已知公共水准点无显著关系。
3)当水准点不多于4 个时,基于EGM2008 模型采用常数模型进行高程拟合,获得高程数据精度最高。
4)当水准点不少于6 个时,基于EGM2008 模型进行高程拟合,平面模型精度高于曲面模型。
本文研究利用少量水准点基于EGM2008 模型实现大地高到正常高的转换,为山区像控点测量和地形图测量提供了可靠的高程数据,通过项目实践总结了一套GNSS 高程转换作业流程,并在同类型的高速公路项目中推广应用,以期为已知水准点少,高程测量困难的工程项目进行高程转换提供参考。
——以大班艺术领域为例

