基于神经网络的两相混合式步进电机反步控制

战家治， 崔皆凡

(沈阳工业大学 电气工程学院，辽宁 沈阳 110000)

0 引 言

两相混合式步进电机因其独特的优势，常应用于工业制造、自动化、军事、航空航天等领域，如机器人、机械手臂、印刷包装设备、数控机床、精密仪器、雷达装置等，步进电机具有广阔的发展前景[1-2]。在一般运行条件下，步进电机直接使用开环控制就能得到较好的运行特性，同时开环系统具有结构简单、维护方便等优点。但开环控制系统存在振荡区，跟踪精度不高，且对系统突加负载，步进电机可能产生失步、堵转等问题，除此之外，电机性能不仅易受负载变化影响，而且运行时还会受参数摄动、摩擦阻力因素以及运行温度等影响，使实现对步进电机的精确控制的难度增大。传统的 PID 控制难以满足步进电机实现高精度位置跟踪的要求。因此，需要设计一种控制器使系统具有较强的位置跟踪性能以及较高的响应速度。

反步设计法的基本思想是将复杂的非线性系统分解成不超过系统阶数的子系统，然后为每个子系统设计部分Lyapunov函数和中间虚拟控制量，一直“后退”到整个系统，将其集成起来完成整个控制律的设计。

目前已有文献对反步控制方法进行研究，例如，文献[3]设计了一种鲁棒反步控制器，提高了永磁同步直线电机的鲁棒性，并且解决了高频噪声等问题。文献[4]将自适应控制与反步控制用于内置式永磁同步电机(PMSM)控制中，可以改善系统的抗干扰性。文献[5]将系统辨识与反步控制结合，提高了伺服系统的鲁棒性和转速稳定性，但是整个系统设计比较复杂。文献[6]设计了一种带有积分环节的反步自适应控制器并运用在PMSM上，验证了在速度方面具有较好的鲁棒性。文献[7]将鲁棒控制与反步控制相结合，提高了永磁同步直线电机的跟踪精度，但仍存在一定的跟踪误差。文献[8]采用了自学习滑模与自抗扰反步结合的控制方法，虽然具有较好的抗干扰性，但跟踪精度仍不理想。文献[9]将神经网络与反步控制结合，并运用到PMSM中，得到了较好的位置跟踪效果。

本文研究的两相混合式步进电机是一个具有非线性、多变量的系统，为了改善两相混合式步进电机的跟踪性能，本文在已有的两相混合式步进电机数学模型基础上，提出了考虑电机电阻变化，黏滞系数变化以及负载扰动情况下的两相混合式步进电机数学模型，并在单一反步控制的基础上引入了径向基函数(RBF)神经网络和自适应率，提出了基于RBF神经网络自适应反步控制策略，利用RBF神经网络逼近系统的非线性部分，以抑制系统非线性的影响，同时设计自适应率，对神经网络的权值进行实时调整,使反步控制器不过于依赖参数的选取，达到对变化对象、随机扰动等因素的良好控制效果,使系统具有较高位置跟踪精度。

1 步进电机数学模型

假设磁路线性且不饱和，忽略定子端部和极间漏磁，忽略定子轭部和极身磁阻，忽略永磁体漏磁。

则两相混合式步进电机在d-q坐标下的电压方程为[10]

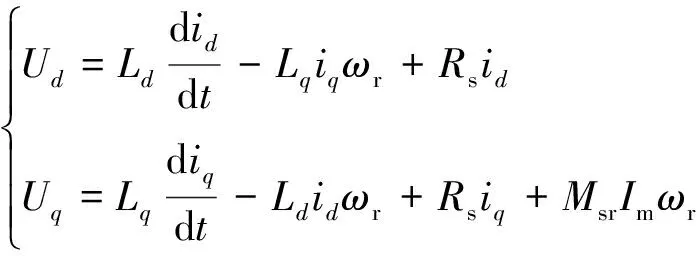
(1)

式中：id和iq为d-q坐标系下的直交轴电流；Ud和Uq为d-q坐标系下的直交轴电压；Rs为定子每相电阻；ωr为转子的电角速度；Msr为定转子之间互感的最大值，Im为假定把永磁体的磁场等效为转子电流建立的磁场的电流值。

(1) 考虑电动机运行时温度对电阻的影响，用R+R0代替Rs[11]：

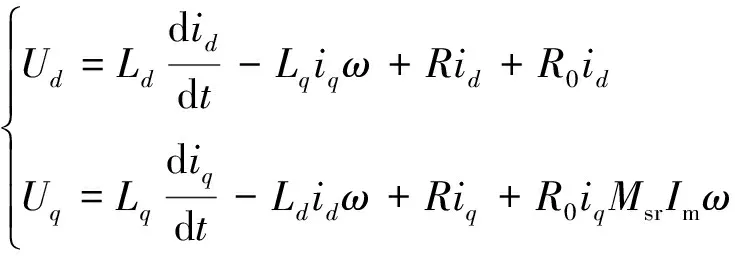
(2)

(2) 电磁转矩表示为

Te=Te0+Th+Tc

(3)

式中：Te0为基本电磁转矩;Th为谐波转矩;Tc为齿隙转矩。

(3) 考虑到电机负载变化、转动惯量和摩擦系数等对机械方程的影响，则：

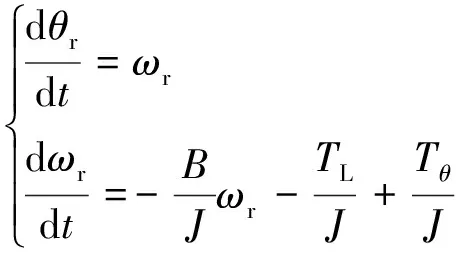
(4)

考虑到电机负载变化TL=TL0+ΔTL，转动惯量的变化J=J0+ΔJ，黏滞阻尼系数的变化B=B0+ΔB。则

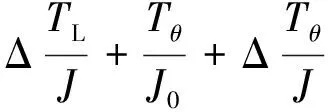
(5)

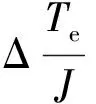
综合式(2)、式(3)和式(5)，可得两相混合式步进电机的数学模型：

(6)

式中：p为齿极对数。

2 基于RBF的反步控制器设计

因为两相混合式步进电机是一个典型的二阶非线性系统[12]，其状态方程可写为

(7)

式中：x1和x2为系统的状态变量，x1为电机运行的转子位置θ，x2为电机转动的角速度ωr。

控制目标是使输出x1跟踪期望轨迹xd，并且所有的信号有界。u为控制输入矢量；f(x)是包含参数或非参数不确定性的非线性函数矢量，是需要利用RBF神经网络逼近的部分；g(x)为与电机有关的系数。f(x)、g(x)的表达式为

(8)

定义角度误差为z1=x1-xd，其中xd为指令信号，则:

(9)

基本的反演控制方法设计步骤如下:

第一步。定义Lyapunov函数

(10)

求导得：

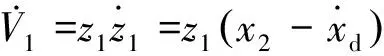
(11)

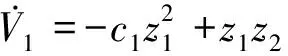
(12)

第二步。定义Lyapunov函数

(13)

求导得：

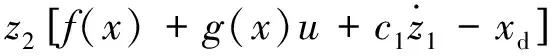
(14)

(15)

c1、c2为反步控制器所选参数，并无实际物理意义。

将式(8)代入式(15)中可得：

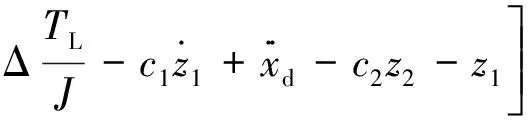
(16)

式中：c2≥0。

则有：

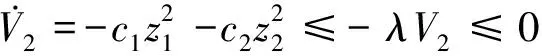
(17)

由式(17)可得，V2(t)≤e-λtV2(0),如果t→∞，则z1→0，z2→0且指数收敛，从而x1→xd，且指数收敛，x2有界。

模型中f(x)是来自步进电机运行各个方面的不确定因素，是非线性项，包括电机运行时的温度变化、黏滞系数以及摩擦阻力变化等，影响着电机的响应速度、稳态误差、跟踪精度。由于f(x)是一个不确定项，本文采用RBF神经网络进行逼近。

3 RBF神经网络设计

RBF神经网络结构选取2-5-1，隐含层引入高斯基函数作为网络函数，整个神经网络的网络算法为

(18)

式中：x为网络的输入，分别为电机运行的转子位置θ和角速度ωr；j为隐含层第j个节点；cj为高斯基函数第j个神经元的中心向量；bj为高斯基函数第j个神经元的基宽；h=[hj]T为网络的高斯基函数的输出；W*为网络的理想权值；ε为网络的逼近误差，ε≤εN;εN为规定最小误差。

网络输入取x=[x1x2]T，则网络输入为

(19)

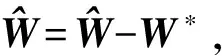
-WTh(x)+ε

(20)

4 控制算法设计与分析

采用RBF神经网络逼近f(x)，根据式(15)，此时的控制律为

(21)

式中：η≥0。

根据上述分析，重新设计Lyapunov函数如下

(22)

式中：γ≥0。

z2[-WTh(x)+ε-ηsgn(z2)]=

z2ε-η|z2|

(23)

取自适应律为

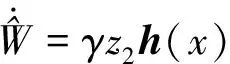
(24)

取η≥εN,则

(25)

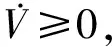
5 仿真分析

为了验证RBF神经网络与反步控制结合在两相混合式步进电机上的控制效果，一般进行可仿真验证。所采用的电机参数如表1所示。

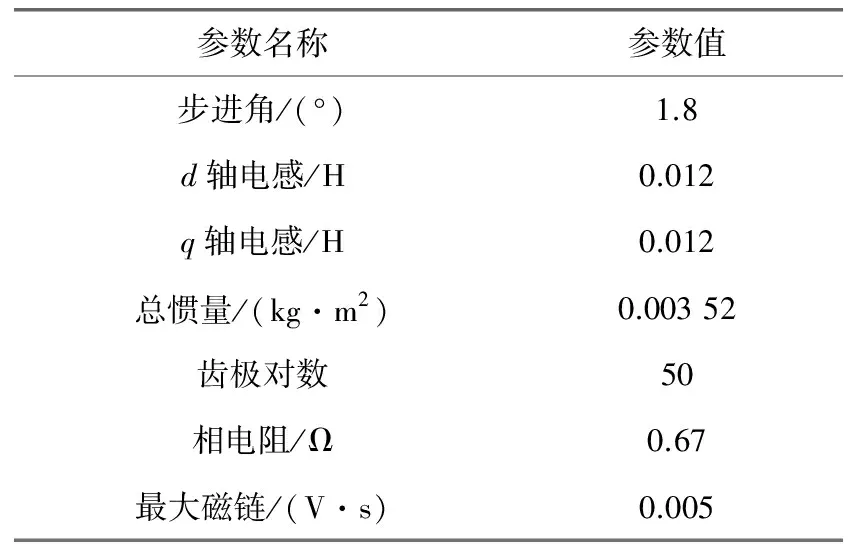
表1 电机的基本参数

针对上述电机，设计基于RBF神经网络的步进电机反步控制系统如图1所示。

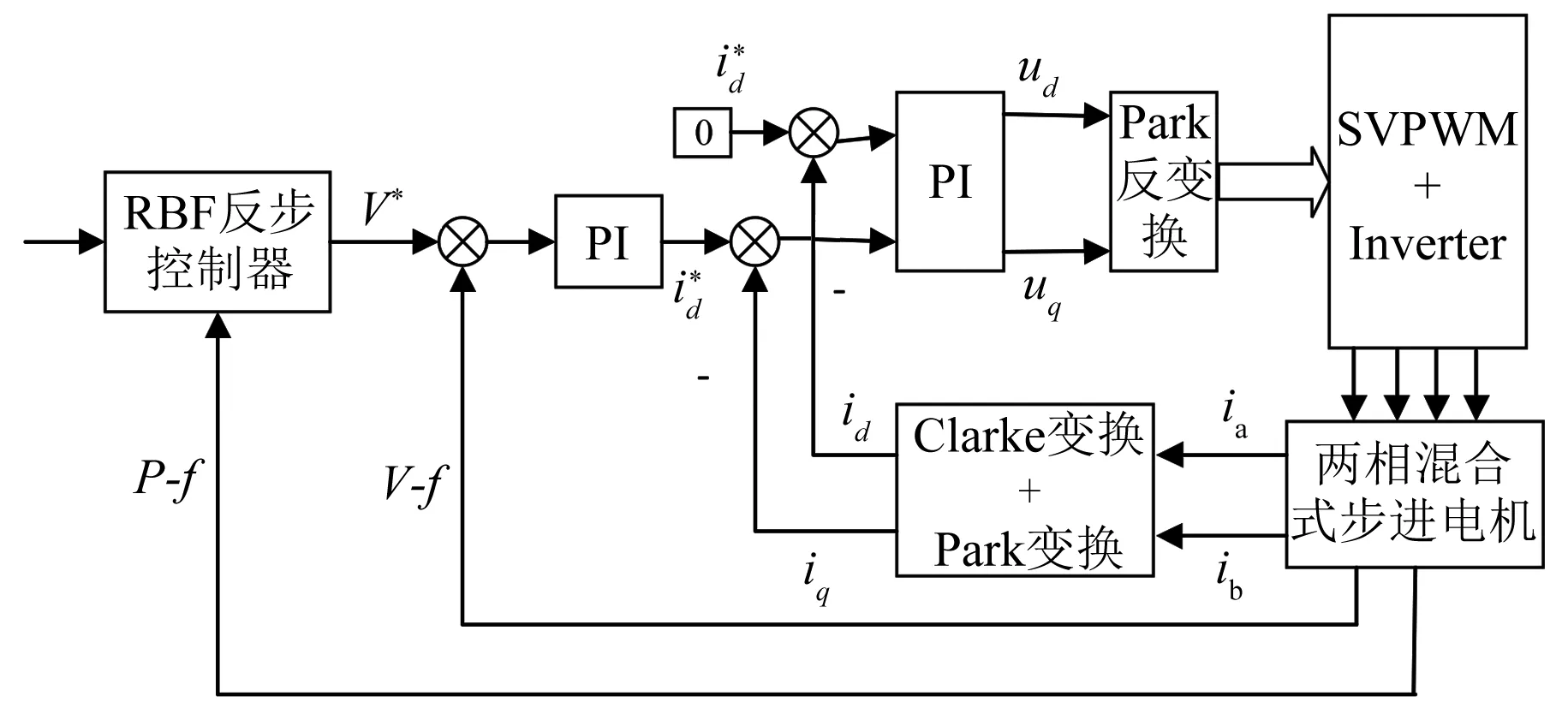
图1 RBF反步控制系统模型

仿真分别在空载和负载条件下，对电机位置环施加正弦信号和阶跃信号进行试验。RBF反步控制器参数如表2所示。

表2 RBF反步控制器参数

对电机施加幅值为3 rad的正弦位置信号，仿真时间为10 s，根据图2所示的电机位置波形所示，基于RBF神经网络的反步控制器的位置波形能较好地跟踪给定的位置信号，而单一反步控制器波形不平滑，且跟踪误差较大。

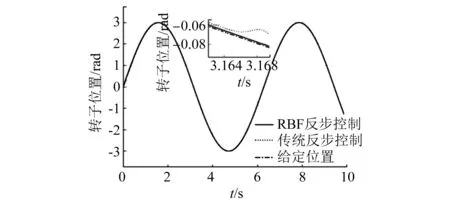
图2 正弦位置波形

图3和图4所示的分别是RBF反步控制和单一反步控制的正弦位置误差波形，可以看出，基于RBF神经网络的反步控制的位置误差较小，且波动较小，最大误差为0.001 52 rad。而单一反步控制的位置误差较大，最大误差为0.111 8 rad。相比之下，改进反步控制最大位置误差仅占单一反步控制位置误差的2%。

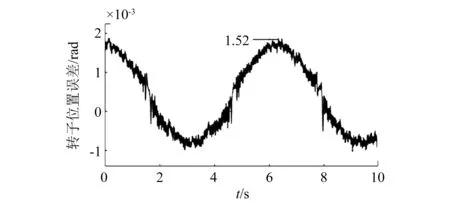
图3 正弦信号下基于RBF反步控制位置误差波形

图4 正弦信号下单一反步控制正弦误差波形

图5所示的是电机带10 N·m负载，从0运行到10 rad的阶跃波形图像，可以看出，加入RBF的控制系统比单一反步控制系统的稳态误差小，且响应时间较短。

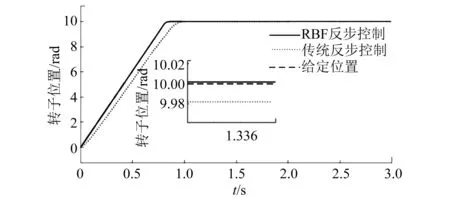
图5 阶跃波形

图6和图7所示的分别是RBF反步控制和单一反步控制的位置误差波形，可以看出RBF反步控制系统响应时间为0.885 s，与单一反步控制系统响应时间1 s相比，响应时间缩短了0.115 s，且RBF反步控制系统稳态误差为-0.001 913 5 rad，与单一反步控制系统的0.2 rad相比减少了0.198 086 5 rad，仅占单一反步控制系统稳态误差的0.01%，并且单一反步控制系统存在一定的波动。而改进反步控制系统基本无波动。由此可知，基于RBF神经网络的反步控制器与单一反步控制器相比，具有较短的响应时间和较好的位置跟踪效果。

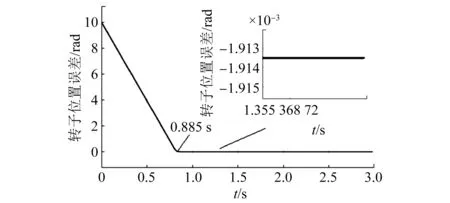
图6 RBF反步控制阶跃误差波形

图7 单一反步控制阶跃误差波形

6 试验研究

为了验证RBF神经网络优化反步控制器的可行性，搭建了步进电机试验平台，试验平台控制对象是57式两相混合式步进电机，步进角是1.8°，主控芯片是STM32F103ZET6。试验平台以STM32作为主控模块，系统主要硬件包括电源模块、控制模块、TB67S109A驱动模块、编码器反馈模块、接口模块(包含SWD接口、串口转换电路)、丝杠滑台以及步进电机组成。

图8 步进电机控制系统试验装置

电机设定给定位置为100 mm，图9、图10分别为改进前后电机空载位置波形误差。可知，优化后的反步控制器响应时间更短，约为0.4 s,且稳态误差也较小。

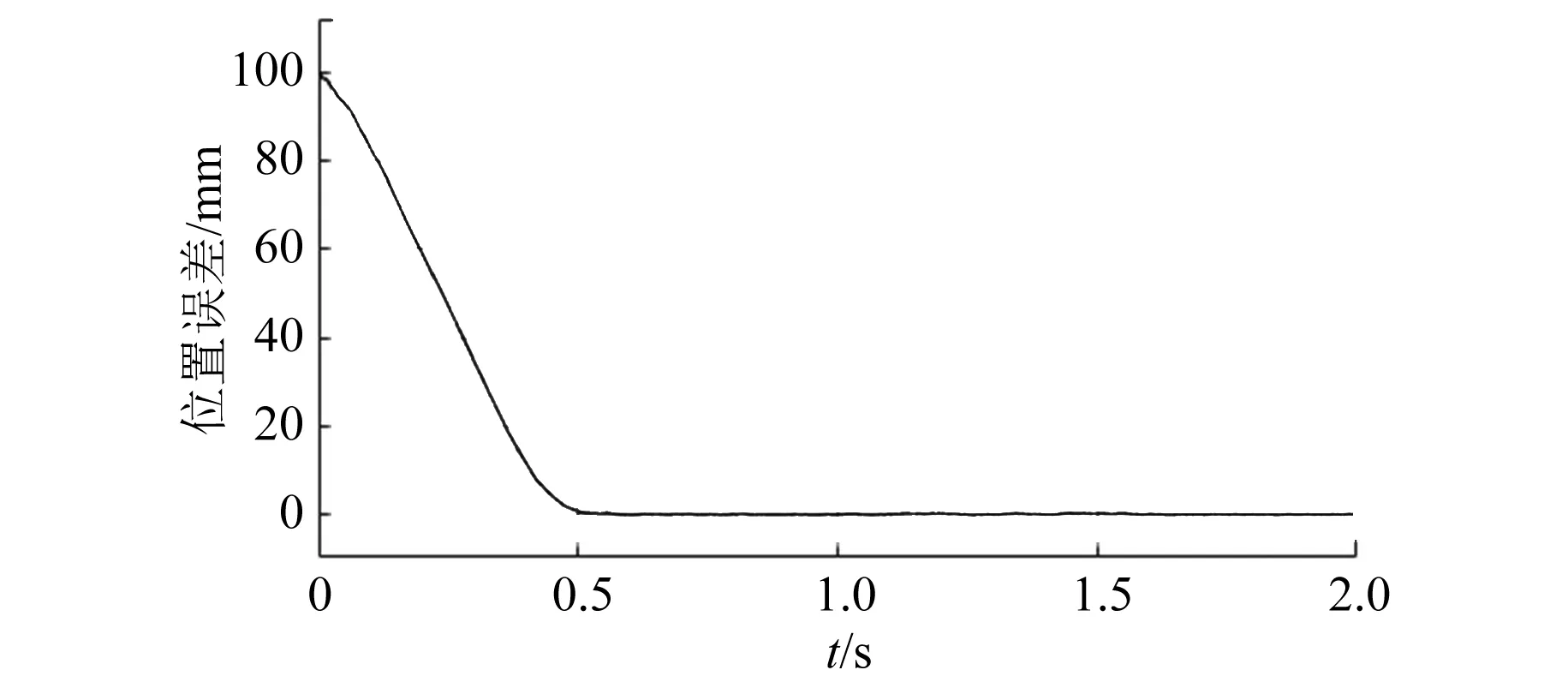
图9 单一反步控制位置误差波形

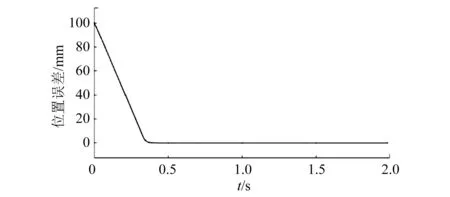
图10 基于RBF反步控制位置误差波形

图11、图12分别优化前后，电机带载5 N时的位置误差波形。可知，RBF优化后的反步控制器响应时间明显减小，约为0.5 s，且跟踪性能明显优于单一的反步控制器。

图11 单一反步控制带载位置误差波形

图12 基于RBF反步控制带载位置误差波形

7 结 语

为了提升两相混合式步进电机控制性能，本文在已有的两相混合式步进电机数学模型基础上，提出了考虑电机电阻变化，黏滞系数变化以及负载扰动情况下的两相混合式步进电机数学模型，并提出了一种基于RBF神经网络的反步控制方法，在单一的反步控制的基础上引入了RBF神经网络来对系统中的非线性项进行逼近，同时引入自适应律对神经网络中的高斯基函数权值进行在线调整。通过与单一反步控制进行对比，证明改进后的反步控制策略，跟踪精度明显提高，同时加快了系统响应速度，设计结果通过仿真与试验得到了验证。