永磁同步伺服系统摩擦力和扰动补偿方法研究

李浩东, 李长兵

(1.广东工业大学 自动化学院，广东 广州 510000；2.广州数控信息科技有限公司，广东 广州 510000)

0 引 言

数控机床、伺服转台等精密伺服系统都对系统的控制精度提出了很高的要求。然而系统的控制精度不可避免地受到包括非线性摩擦力在内的系统扰动的影响。因此为了提高系统的控制精度，必须采取合适的方法对系统扰动进行补偿来消除或减弱系统扰动的影响。系统中摩擦力补偿的方法一般按照是否基于摩擦力模型来区分。基于摩擦力模型的补偿方法主要通过建立系统中摩擦力的数学模型实现对摩擦力模型特性的准确描述，通过数学模型观测出系统的摩擦力矩并进行补偿[1-3]，基于摩擦力模型的方法的补偿效果依赖于模型的准确性，越能描述系统摩擦力特性的模型，其补偿效果越好。常见的摩擦力模型有库伦摩擦力模型、库伦+黏性摩擦力模型、Dahl模型、Stribeck模型、LuGre模型、Maxwell-slip模型等。LuGre模型[4]能够很好地描述摩擦力的动静态特性，包括Stribeck特性、爬行、极限环振荡、摩擦记忆、变静摩擦力等，模型结构比Maxwell-slip模型简单，因此LuGre模型是当下研究的热点之一。不基于模型的摩擦力补偿方法主要是将摩擦力当作普通扰动处理，如利用PID控制器、扰动观测器(DOB)[5]、神经网络等智能控制方法[6]实现对摩擦力扰动的补偿。由于摩擦力的强非线性，不基于摩擦力模型的方法很难实现最佳的补偿效果，且一些智能控制算法往往设计较为复杂，占用大量的控制资源，实际难以推广应用。

采用固定参数模型的摩擦力补偿方法中需要精确辨识出系统的摩擦力模型参数，考虑到实际系统运动过程中，润滑条件变化，表面磨损等会使摩擦力模型参数发生变化导致摩擦力出现过补偿和欠补偿的现象。文献[7]利用双观测器实现对LuGre模型中不可测状态量的观测，并利用李雅普诺夫稳定性理论设计自适应控制器实现了摩擦力的在线辨识和补偿，克服了摩擦力参数变化导致补偿不佳的问题，但是双观测器的结构过于复杂，且自适应控制器设计过程中未考虑系统其他扰动的影响。在伺服系统中，对于系统参数摄动，系统不确定因素，系统环境变化等扰动一般采用DOB观测器对其观测和抑制[8]，常用如DOB、扩张状态观测器(ESO)、降阶扩张状态观测器(RESO)[9]等，此类观测器从本质上都是将系统的扰动当作集总扰动来处理，因此对于摩擦力补偿阶段出现的欠补偿和过补偿可以将其看作是系统集总扰动的一部分，利用DOB进行补偿。文献[10]通过将基于Stribeck模型的摩擦力补偿方法和DOB相结合，在补偿摩擦力的同时，利用DOB实现对系统内扰动的补偿，然而DOB的补偿效果受限于Q滤波器的带宽的限制。

本文提出一种基于LuGre摩擦力模型和RESO相结合的摩擦力补偿方法，利用速度和转矩信息辨识出LuGre摩擦力模型参数，将摩擦力模型观测出的摩擦力矩以电流的形式补偿到电流环的控制输入端，同时考虑到RESO具有结构简单、抗扰动性能强的优点，利用RESO来观测补偿系统中的其他集总扰动，减弱摩擦力和扰动对系统造成的影响，提高系统的控制精度。

1 永磁同步伺服系统动力学分析

永磁同步伺服系统由表贴式永磁同步电机(PMSM)通过联轴器联结滚珠丝杠副构成。在矢量控制方法中，电机通过坐标变换在d-q坐标系下的数学模型表示为[11]

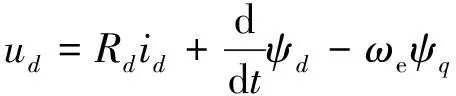
(1)

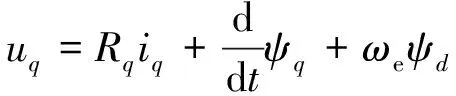
(2)

ψd=Ldid+ψf

(3)

ψq=Lqiq

(4)

式中:Rd、Rq、Ld、Lq、ψd、ψq分别为d、q轴的定子电阻、电感和磁链；ψf为永磁体磁链。

对于精密伺服系统，系统的刚性一般很大，可以忽略系统中联结处的间隙，将机械部分看作刚性系统，则系统的动力学方程可简化为

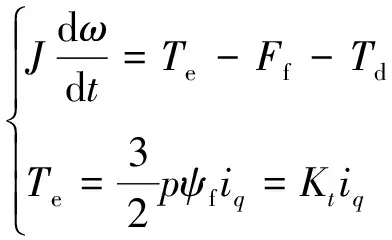
(5)

式中:J为系统总的转动惯量；Kt为转矩系数；p为电机极对数；Ff为系统的摩擦力；Td为系统中其他扰动集合。

2 系统摩擦力模型的建立与模型参数辨识

2.1 系统摩擦力模型的建立

LuGre摩擦力模型是一种鬃毛模型，即假设物体表面由无数鬃毛构成，对接触的物体表面施加作用力时，接触面的鬃毛产生形变进而产生摩擦力。对于永磁同步伺服系统，LuGre模型可以描述出系统中的静摩擦力，滑动摩擦力，库伦摩擦力，同时在预滑动阶段还能描述可变的静摩擦力。LuGre摩擦力数学模型为[12]

(6)

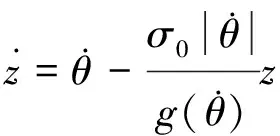
(7)

(8)

式中：Ff为摩擦力；z为鬃毛形变量；Fc、Fs、Vs和B为摩擦力中的静态参数，分别为库伦摩擦力、静摩擦力、切换速度和黏滞摩擦系数；σ0和σ1为鬃毛刚度系数和微观阻尼系数。

2.2 摩擦力参数辨识

为了能准确观测出系统摩擦力的大小还需要对模型的参数进行辨识。LuGre模型参数的离线辨识分静态参数和动态参数辨识两步进行。静态参数通过摩擦力的Stribeck静态特性曲线辨识得到，动态参数通过已辨识出的静态参数和位置响应发生振荡时的力矩信息辨识得到。

2.2.1 摩擦力静态参数辨识

空载运行时通过给一组速度给定信号测得稳态时相应的转矩值，由系统的运动方程式(5)可知，考虑摩擦力为系统的主要扰动，匀速运动时系统的给定转矩与系统的摩擦力矩近似相等。假设速度正反运动时的摩擦力模型参数是相同的。通过测得的数据可得系统摩擦力的Stribeck曲线如图1所示。

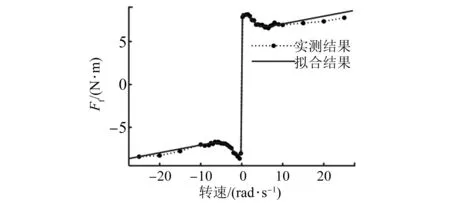
图1 系统Stribeck曲线

(9)

基于式(9)对Stribeck曲线进行拟合辨识得到模型中的静态参数，辨识结果如表1所示。

表1 静态参数辨识结果

2.2.2 摩擦力动态参数辨识

LuGre摩擦力模型是一种非线性系统，内部状态z不可测量，且静态参数和动态参数存在耦合，采用最小二乘法和单纯形法等难以保证辨识精度的收敛性，而遗传算法作为一种启发性算法，不需要对象的模型信息，同时能够很好地避免局部最优，鲁棒性强，因此采用遗传算法进行辨识[13]。

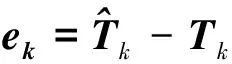
(10)

定义目标函数:

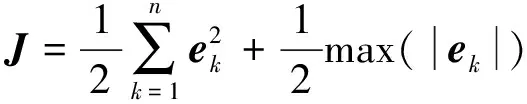
(11)

动态参数辨识过程中的转矩信息无法直接测量，因此利用系统的转矩方程通过试验中系统的q轴电流转换得到。遗传算法可利用MATLAB遗传工具箱实现。动态参数的辨识结果如图2所示。

图2 力矩曲线对比

由图2可知，辨识得到的摩擦力矩曲线和测得转矩曲线基本保持一致，可以认为辨识的动态参数是准确的，辨识结果如表2所示。

表2 动态参数辨识结果

3 摩擦力补偿控制方法设计

3.1 摩擦力前馈补偿

系统中的摩擦力矩可以看作是施加在负载端的反向力矩，因此可以通过在电机的控制力矩上加上相等的力矩补偿量来抵消摩擦力矩造成的影响。系统采用矢量控制策略，电流环和速度环采用PI控制器，位置环采用比例+速度前馈的控制方法，系统的控制结构框图如图3所示。

图3 系统控制结构框图

通过LuGre模型观测出系统的摩擦力矩，利用系统的转矩方程将摩擦力矩转换成q轴电流iTf，通过将iTf补偿到电流的控制输入端即可实现对系统中摩擦力矩的补偿。在该补偿方案中，为避免引入反馈环节影响到系统的稳定性，摩擦力模型的输入信号为速度给定信号，补偿方案结构简图如图4所示。图4中，Kt为转矩系数，J为系统总的转动惯量，L为电机定子电感，R为电机定子电阻。

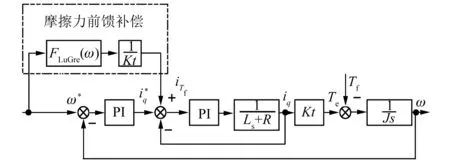
图4 摩擦力前馈结构简图

3.2 扰动补偿

摩擦力前馈补偿方案中补偿的效果取决于摩擦力模型参数辨识结果的精确性，在实际系统中，摩擦力参数会根据系统运行实时状况,例如润滑条件等发生变化，导致摩擦力存在欠补偿和过补偿的问题。实际的伺服系统中除摩擦力之外还有如系统参数摄动、转矩脉动等的扰动，为进一步提高系统的精度，采用RESO对此类扰动进行观测补偿。

空载条件下，系统的运动方程式(5)可以化为

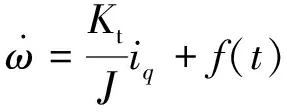
(12)

式中：f(t)为系统中的集总扰动。

设x1、x2分别代表速度ω和扰动f(t)的状态变量。则式(12)可转化为

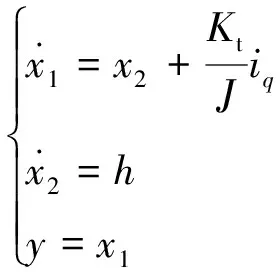
(13)

取z1为x1的观测值，z2是x2的线性观测器值。可设计扩张状态观测器为[13]

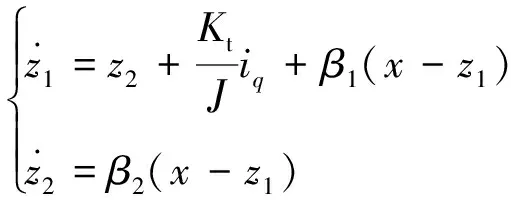
(14)

β1、β2为相应的参数与观测器带宽有关，实际系统中为了确保输出量的精确度，输出的位置信息和速度信息可直接通过编码器获得，因此:

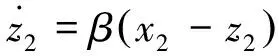
(15)

由式(9)和式(12)可得：

(16)

式(16)中状态变量x1的微分可能会引入噪声，对其进行改写，定义新的状态变量：

znew=βx1-z2

(17)

则降阶状态观测器可设为

(18)

同样观测器的参数β可以通过系统的带宽求得，并可以根据实际情况调节。降阶扰动观测器补偿结构框图如图5所示。

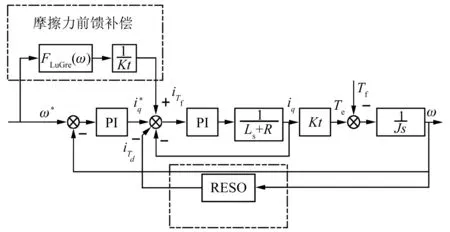
图5 RESO补偿结构框图

4 摩擦力补偿试验结果与分析

4.1 试验平台

本文利用滚珠丝杠平台对所提方法进行试验验证，平台如图6所示。电机采用广州数控130SJT-100D型PMSM，驱动采用广州数控GR2050T系列驱动，丝杠平台采用硬轨平台，系统的位置信息由电机端17位绝对值编码器得到。丝杠导程为5 mm，电机转动惯量为Jm=2.42 g·m2，联轴器转动惯量为Jc=0.046 4 g·m2，滚珠丝杠和直线运动部件折合的总转动惯量为Jb=0.160 213 g·m2。

图6 精密滚珠丝杠试验平台

4.2 试验结果

为了验证摩擦力等扰动对系统位置跟踪精度的影响，位置参考信号分别给定0.5 sin(πt-0.5π) mm和2.5 sin(πt-0.5π) mm不同幅值的正弦信号，消除特定位置引起的位置波动对试验准确性的影响。图7为系统未进行摩擦力和扰动补偿时的位置跟踪误差曲线。

图7 系统未补偿时系统位置跟踪误差

由图7可知，位置的跟踪误差存在一个较大的峰值，误差峰值在正弦信号的峰值处,这是由于系统运动换向时，摩擦力导致位置出现平顶现象造成的位置跟踪误差，参考信号为0.5 mm时，误差约为±14.5 mm，参考信号幅值为2.5 mm时，误差约为±24 mm。

图8为系统摩擦力前馈补偿下的位置跟踪误差，采用摩擦力前馈补偿后，参考信号幅值为0.5 mm时，系统的位置跟踪误差约为±5.6 mm，参考信号幅值为2.5 mm时，位置跟踪误差为±9.9 mm。比未补偿时位置跟踪误差减小了60%以上，证明了摩擦力前馈补偿能够有效的提高系统的控制精度。图9为系统在摩擦力补偿的基础上利用RESO对系统中的扰动进行补偿后的位置跟踪误差，与图8相比，参考信号幅值为0.5 mm时，系统的位置跟踪误差约为±3.5 mm，参考信号幅值为2.5 mm时，位置跟踪误差为±6.5 mm，比摩擦力补偿时位置跟踪误差减小了35%左右，进一步提高了系统的控制精度，验证了所提方法的有效性。

图8 摩擦力前馈补偿下位置跟踪误差

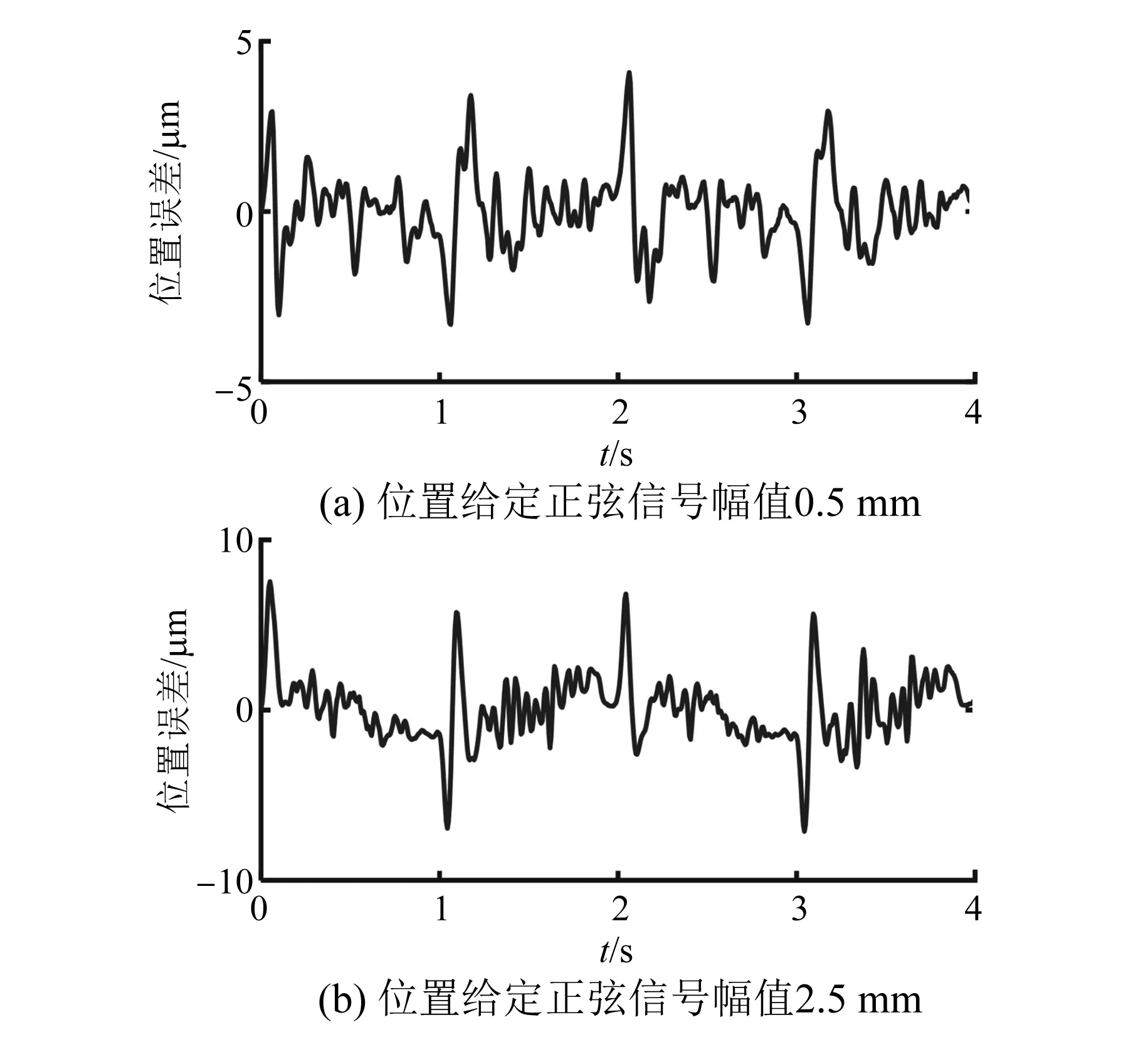
图9 摩擦力前馈补偿和RESO共同作用下位置跟踪误差

5 结 语

本文提出一种将基于LuGre模型的摩擦力前馈补偿和RESO结合起来的系统摩擦力扰动补偿方法，通过Stribeck特性曲线和力矩信息辨识出LuGre模型静态和动态参数，利用LuGre模型实现对系统中摩擦力矩的准确观测，并通过前馈补偿方案减弱了系统摩擦力对位置跟踪精度造成的影响。同时设计降阶扰动观测器实现对系统中其他集中扰动力矩的补偿，进一步提高了系统的控制精度。试验结果显示所提方法比未进行任何补偿时位置的跟踪误差减小75%左右,比仅采用LuGre模型的摩擦力前馈补偿，位置控制误差减小35%左右，证明了所提方法的有效性。