基于电机参数在线修正的高速永磁同步电机无位置传感器算法研究*

陶楷文， 储剑波

(南京航空航天大学 自动化学院 ，江苏 南京 211100)

0 引 言

在多电飞机电动环境控制系统中，高速永磁同步电机(HSPMSM)驱动压气机进行环控[1]，系统出于裕度考虑往往会为HSPMSM配备一套无位置传感器算法。然而无位置传感器算法的可靠运行很大程度取决于其数学模型的准确建立。环控系统中HSPMSM运行环境恶劣，高速大功率工况下伴随的高温高振等因素，使得电机参数在运行过程中发生变化，从而导致无位置传感器算法的数学模型偏差，使得位置观测器输出估算位置信息失稳，最终导致系统波动剧烈甚至发散。因此，为保证无位置传感器算法可靠运行，必须对电机参数进行有效监测。

扩展卡尔曼滤波(EKF)理论是一种最优估计方法，因其收敛速度快、估计精度高且抗干扰强的优点而受到广泛关注。清华大学Xiao等[2]构建了估算转子永磁体磁链幅值和方向的卡尔曼滤波器，在线监测永磁体磁场状况，解决了噪声环境下的永磁体磁链辨识困难的问题[3]。文献[4]提出采用扩展卡尔曼滤波器对组合航天器惯量参数进行辨识，该算法克服了由于模型简单导致转动惯量信息辨识不完整的缺点。然而由于电机参数的在线辨识以定子电压方程为基础，想要同时辨识电感，定子电阻与转子磁链为无位置传感器算法服务、定子电压方程会存在缺秩问题。在不添加额外测量电路的条件下，为解决缺秩问题，一类方法是将某个电机参数视为已知值或采用分步辨识[5-6]，以减少同时辨识的电机参数个数。另一类方法是通过注入激励信号获得新的方程，从而构成辨识的满秩模型[7]。但这两种方法算法复杂、调试难度大，难以运用到运行工况恶劣的无位置传感器HSPMSM系统中。

本文针对所采用的基于扩展反电动势法(EEMF)的无位置传感器算法[7]，通过稳定性分析法到得参数依赖性特点，针对算法高依赖性参数进行基于EKF的在线辨识。能够避开全参数辨识所导致的缺秩问题，降低了算法复杂度，只需要实时修改位置观测器模型中具有高依赖性的参数，即可达到基于无位置传感器算法的HSPMSM系统稳定运行。最后，通过MATLAB/Simulink仿真验证了分析所得无位置传感器算法参数依赖性特点与所提方法的正确性与有效性。

1 无位置传感器算法设计

d-q轴旋转坐标系中永磁同步电机(PMSM)的传统电压方程：

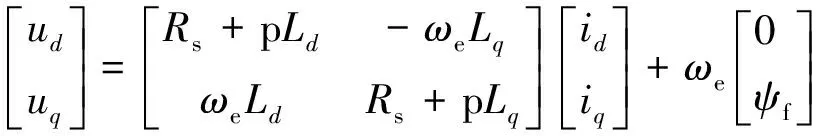
(1)

式中：ud、uq分别为d、q轴电压;id、iq分别为d、q轴电流;Ld、Lq分别为d、q轴电感;Rs为定子电阻;p为微分算子;ψf为永磁体磁链;ωe为转子电角速度。

考虑表贴式电机(Ld=Lq=Ldq)，并将式(1)进行数学处理[6]，电压方程变换到γ-δ估计旋转轴坐标系下，得到式(2)：

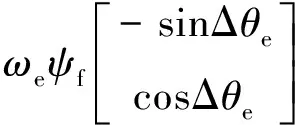
(2)

利用式(2)建立数学模型，求取位置信息。基于估计旋转坐标轴下扩展反电动势的无位置传感器算法控制框图如图2所示。

图2 无位置传感器控制算法方案框图

2 参数依赖性分析

对基于无位置传感器的HSPMSM系统进行小信号模型建立和稳定性分析，改变电机参数绘制系统特征根轨迹图，定性分析无位置传感器算法模型的参数依赖性。

2.1 系统小信号模型建立

针对PMSM模型状态方程如式(3)：

(3)

式中:J为转动惯量;p为电机极对数;TL为负载转矩;ωr为转子机械角速度。

将式(3)进行小信号模型处理，选取稳态工作点进行离散化：

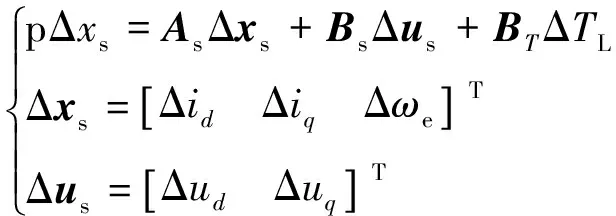
(4)

对无位置传感器算法进行小信号模型建立。利用式(2)，忽略反电动势中微分项，考虑在运行过程中Δθe项近似为0，利用等价无穷小原理可得：

(5)

结合图2控制框图即可写出位置观测器局部状态方程：

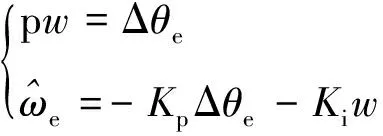
(6)

式中:w为Δθe积分项;Kp、Ki分别为位置观测器比例系数和积分系数。

在此基础上选取稳态工作点进行离散化，建立小信号模型。同样，系统中转速、电流调节器也利用该思路进行小信号模型建立，最终整合成式(7)：

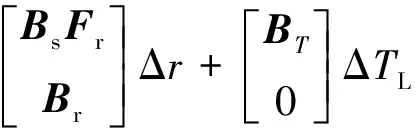
(7)

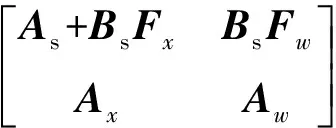
式(7)详细推导过程见文献[8]。改变转移矩阵中电机参数，可以得到系统关于该参数的特征根轨迹图，从而获得位置观测器的电机参数依赖特性。

2.2 稳定性分析

稳定性分析参数如表1所示，改变电机方程中各个参数得到对应特征根轨迹图，当所有特征值的实部均为负值时，认为系统受到干扰后能够回到稳定状态。

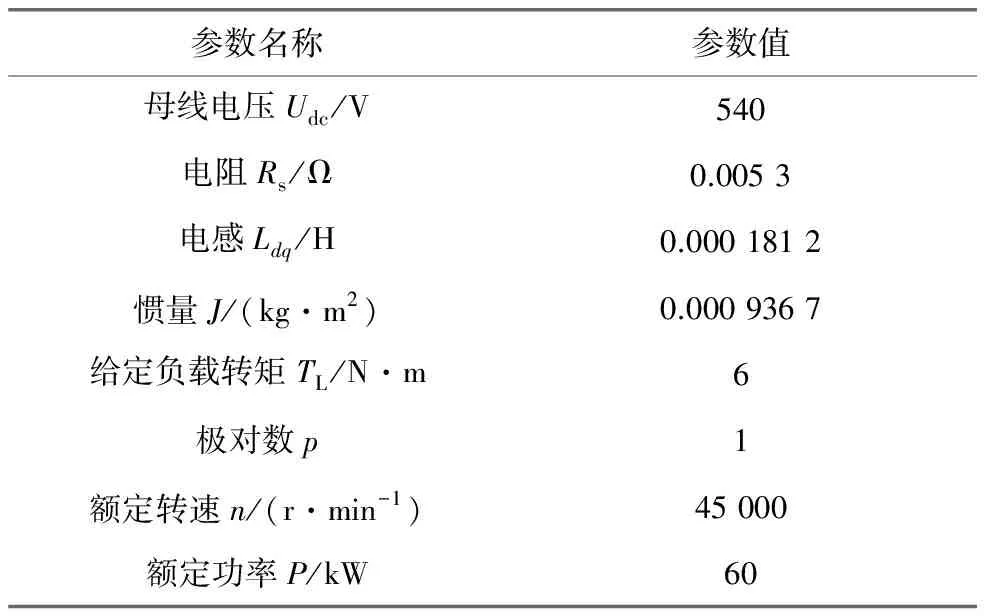
表1 稳定性分析参数

图3为电机参数Ldq(考虑表贴式电机)的特征根轨迹图，转速、电流环带宽分别为10、1 000 Hz[9]，无位置传感器算法带宽选取为115 Hz。采用id=0的PMSM矢量控制方法。电机运行于45 000 r/min时，风机载为6 N·m。由图3可得，当无位置传感器算法参数电感等于实际电感时，系统特征根均分布于左半边，根据李雅普诺夫稳定性判据可知系统稳定。当实际电感增大时系统向左移动，趋于稳定。而实际电机电感减小至0.62倍时，其特征根移动到右半面，系统发散，该无位置传感器算法关于电感参数较为敏感。

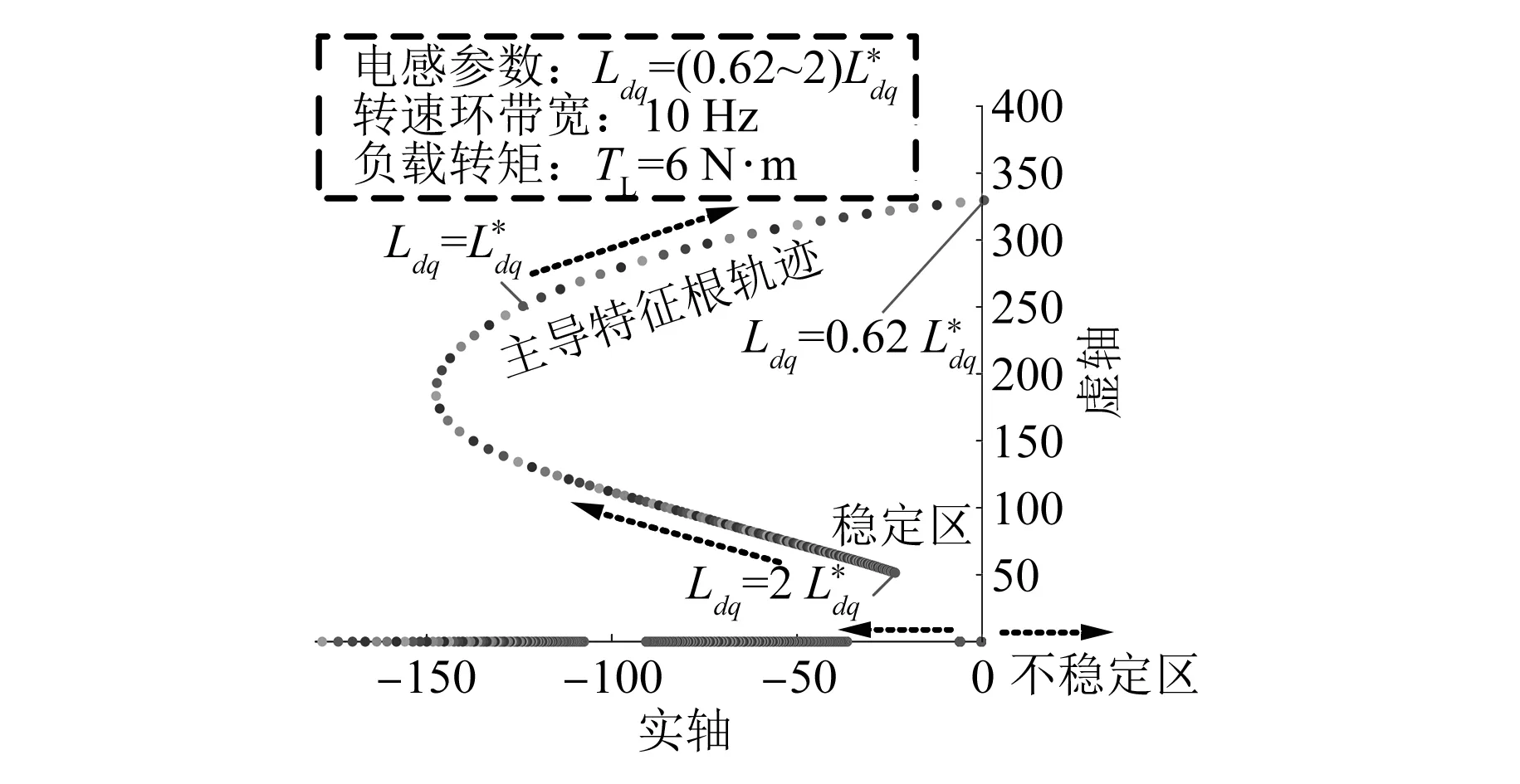
图3 基于变实际电感参数的特征根轨迹

绘制出关于电机定子电阻参数与磁链参数的主导特征根轨迹，发现这两个电机参数的变化几乎不影响系统稳定性。图4所示，将定子电阻由0.1倍变化至100倍，系统所有特征根均分布于左半平面，因此，该算法关于定子电阻有低参数依赖性，磁链参数同样如此。

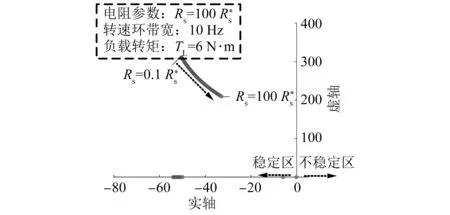
图4 基于变实际电阻参数的特征根轨迹

综上可得，基于EEMF的无位置传感器算法仅关于电机电感具有高依赖性，与定子电阻与磁链参数较低依赖性，实时在线监测电感参数即可保证HSPMSM系统稳定运行。

3 PMSM电感及电阻在线辨识

3.1 扩展卡尔曼滤波观测器

因为PMSM为非线性系统，而传统卡尔曼滤波只适用于线性系统，所以为实现非线性系统的卡尔曼滤波，目前普遍采用按最优状态估计线性化的卡尔曼滤波方程，即扩展卡尔曼滤波方程。非线性状态方程描述如下

(8)

式中:带“^”的变量表示状态估计量;V(k)表示系统噪声的协方差，考虑了实际系统扰动和模型参数的不确定性和可变性;W(k)表示测量噪声的协方差，考虑了所有测量噪声和测量的不准确性。

扩展卡尔曼滤波主要由两个循环步骤组成。

(9)

式中：Q(t)是状态方程(8)中系统噪声的自相关矩阵，由一个对角阵、一个时变矩阵和一个非时变对角阵叠加组成，实际系统中由于采样时间的限制，使用一个非时变对角阵Q代替。因为及模型中A′仍含有状态变量分量，所以还需对系统模型进行线性化处理，即求系统方程对状态变量x的偏导，记为Fk:

(10)

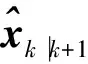
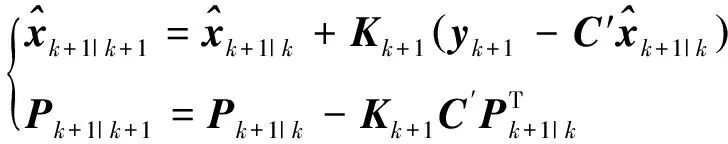
(11)

式中：Kk+1为卡尔曼滤波增益矩阵，关联了状态预测和测量反馈校准两个阶段，反映了卡尔曼滤波的实质。

因此卡尔曼滤波估计的关键是加权增益矩阵Kk+1的选择。Kk+1的表达式如下

Kk+1=Pk|k+1C′T(CPk+1|kC′T+R)-1

(12)

式中:测量噪声协方差矩阵R(t)同样使用一个非时变对角阵R描述。

因此设计卡尔曼滤波增益Rk+1的关键是确定P0|0、Q、R的值。

3.2 PMSM电感在线辨识

因为卡尔曼滤波算法一般用于线性系统中，所以需要对连续的状态方程式(1)进行离散化，表达式为

(13)

离散化后的系统状态变量x(k)=[id(k)iq(k)Rs(k)/Ldq(k) 1/Ldq(k)]T,输入变量y(t)=[ud(k)uq(k)]T,输出变量y(t)=[id(k)iq(k)]T。进而对式(13)求偏导计算出Fk:

(14)

按照状态预测与状态更新步骤即可在线辨识Rs/Ldq与1/Ldq。

3.3 缺秩问题

构建的4阶扩展卡尔曼滤波观测器并不能够使辨识值收敛于真实值，其根本原因在于所构建的观测器并不满足满秩要求，缺秩问题导致系统辨识值存在多解情况。针对该问题利用李导数[10]进行观测器满秩分析，定义矩阵O：

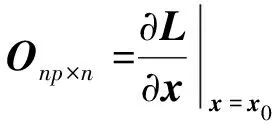
(15)

式中:L为系统可观判别矩阵;由n个k阶李导数组成;np为自变量x的个数;n为观测器的阶数。

最终求得O矩阵，保证其满秩即可保证局部弱能观，即构建的四阶卡尔曼滤波观测器有唯一解。O矩阵经化简如下：

(16)

最终系统满足iq≠0,ωe≠0,卡尔曼滤波观测器满秩。

4 仿真与试验结果

基于电机参数在线修正的EEMF无位置传感器HSPMSM系统控制框图如图5所示。

图5 HSPMSM系统控制框图

在MATLAB/Simulink中对该方法进行了模型搭建和仿真研究，仿真中的电机参数与各调节器参数与稳定性分析中的各参数一致，具体电机参数如表1所示。在0 s给定转速30 000 r/min，1 s时电机电感开始均匀下降，1.5 s时下降至初始值72%。为进一步验证动态情况，在2 s时给定转速35 000 r/min观察转速响应情况。

图6给出了在电机电感变化情况下，基于EEMF无位置传感器HSPMSM系统运行状况。可知在电感变小后，系统出现转速振荡现象，动态效果也相应变差，最终稳态下转速波动达到了6 000 r/min。其原因在于电感变化导致位置观测器数学模型发生偏差，也验证了图3特征根轨迹趋势，减小电感系统特征根向虚轴移动，根据李雅普诺夫定理可知系统趋于不稳定，越靠近虚轴系统噪声则会越明显，使得系统出现较大转速波动。若继续减小电感，系统将出现发散现象。

图6 无位置传感器算法电感依赖性分析

图6验证了该无位置传感器算法关于电感参数的高依赖特性。图7给定电机定子电阻Rs从0.1倍初始值增至100倍，位置观测器中的定子电阻值恒为定子电阻初值Rs，转速波形几乎没有任何改变，验证了EEMF算法定子电阻的低依赖性。

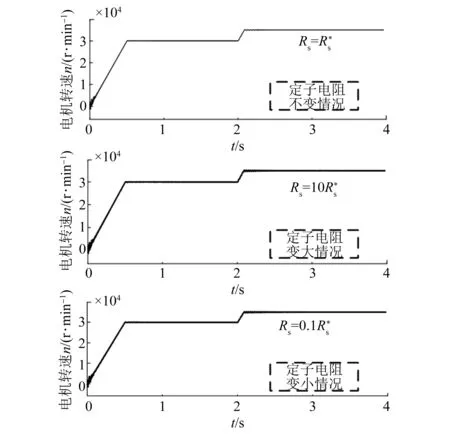
图7 EEMF算法电阻依赖性波形图

图8给出了在空载下EKF观测器辨识结果，辨识值不能收敛于实际值，辨识Rs/Ldq值出现了发散现象，辨识1/Ldq收敛于错误值。仿真与理论对应，当电机处于空载时，所构建的四阶卡尔曼滤波观测器缺秩，式(16)矩阵的秩为2，导致四阶观测器存在多解，使得观测错误。图9给出了电机带载情况下的辨识结果，可知在iq≠0的情况下四阶卡尔曼滤波观测器满秩，能够正确辨识出电阻与电感值。

图8 空载情况下EKF辨识波形

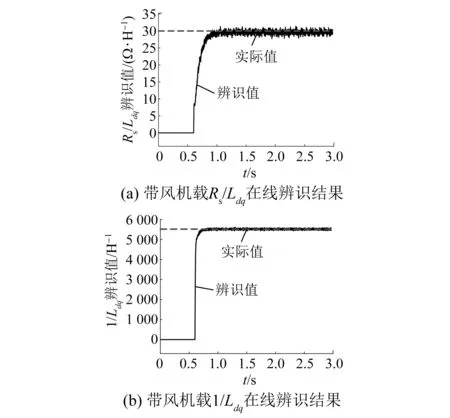
图9 带载情况下EKF辨识波形

对基于EKF在线监测电感的无位置传感器HSPMSM系统进行仿真，给定转速为40 000 r/min，在0.6 s时开始在线监测电机电感并将辨识值送至无位置传感器算法模型以进行修正，2 s时刻升速至45 000 r/min。图10为最终无位置传感器算法输出估计转速与实际电机电感变化波形，估计转速在随着电机电感变化后不会出现转速振荡现象，动态与稳态性能良好。图11给出运行过程中转速误差与角度误差情况，转速误差控制在±150 r/min以内，45 000 r/min转速下稳态精度达到0.33%以内，稳态角度误差也控制在0.01 rad。

图10 基于电机参数在线修正的HSPMSM系统输出波形

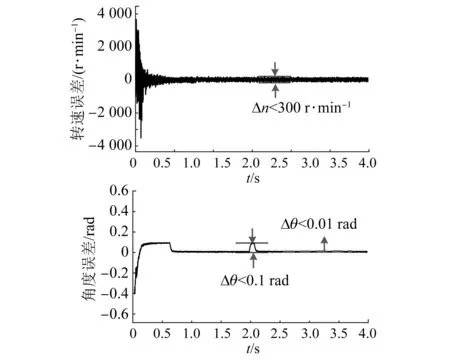
图11 改进算法输出误差情况

图12给出了45 000 r/min转速下估计角度与实际角度对比波形以及角度误差情况，角度误差控制在0.01 rad，高转速下该改进后无位置传感器算法能够稳定运行。图13为扩展卡尔曼滤波观测器输出电感辨识结果，观测器能够实时观测到电机电感实际值。

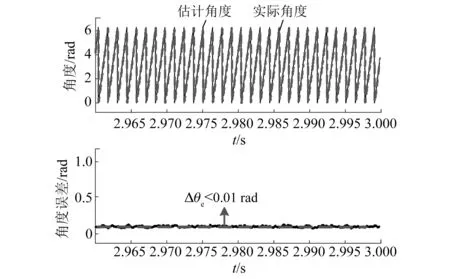
图12 改进算法角度估算波形

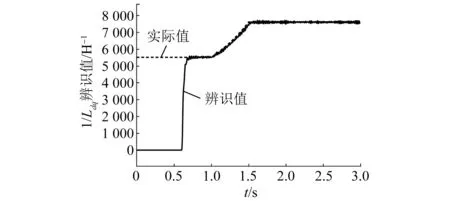
图13 基于EKF在线辨识的电感在线监测波形

5 结 语

本文利用基于小信号模型的稳定性分析法研究了基于估计旋转坐标系下扩展反电动势的无位置传感器算法电机参数依赖特性，针对算法高依赖性参数通过卡尔曼滤波理论构建观测器实现在线监测，实时修正无传感器算法模型，避免了全参数辨识带来的缺秩问题，极大地降低了参数辨识算法复杂度。最后，在仿真中验证了无位置传感器算法参数依赖性与改进方案的可行性与有效性。