城市建成区路侧停车规划模型及算法
杨圣文,李 特,刘庆华,习文辉,杨 敏
(1. 西南林业大学 机械与交通学院,云南 昆明 650233; 2. 昆明理工大学 城市学院,云南 昆明 650051;3. 云南省交通科学研究院有限公司,云南 昆明 650000)
0 引 言
随着城镇人口的增加和机动车保有量的快速提升,停车泊位出现供需不足的情况,严重影响城市交通,如何合理规划停车泊位成为静态交通亟需解决的问题。我国停车研究起步较晚,国内学者基于城市人口规模、城市用地规模、机动车保有量、交通政策和机动车OD预测5种方法计算城市停车需求。为降低设置路侧停车泊位对路网通行能力的影响,国内外学者对泊位优化的研究主要从路侧停车行为对交通的影响、通过管理策略提高泊位周转率降低对道路交通的影响、考虑不同停车规划模型对道路交通的影响等3个方面开展。
路侧停车行为对交通的影响方面,曹文娟等[1]从三方面提出了双层规划模型,提高路网通车效率,减缓路侧停车行为对车辆行驶的影响;张月等[2]阐述了路侧停车行为对城市交通的干扰原因,基于4个因素建立了道路周边用地性质与停车行为的映射关系;邵长桥等[3]建立了车辆进、出频率与影响时间的定量关系模型,从车道宽度、侧向净空及车辆进、出频率3个方面对通行能力进行折减,得到路侧停车与路段通行能力的关系模型;王国娟等[4]基于层次分析法对商业区路内停车管理水平进行评价。
通过管理策略提高泊位周转率降低对道路交通的影响方面,D.C.SHOUP[5]提出了一种新的停车与路径选择网络模型,具体表现为停车类型、管理策略(包括费用、停车场容量和占用率、网络位置)与进入路线的关系;LIU Wei等[6]基于MFD模型描述了超负荷的道路中车辆寻找泊位所增加的巡航成本;A.MILLARD-BALL等[7]建立了停车占用率与找到泊位的概率和巡航次数之间的关系,提出控制最优泊位占用率为60%~80%可减少50%的巡航交通量。
考虑不同停车规划模型对道路交通的影响方面,杨忠振等[8]采用排队论理论,创建双层规划模型,优化城市中心商业区停车方案;王艳等[9]考虑动态多时段的停车需求,在总投资最小的条件下,建立步行距离最短的模型;何胜学等[10]建立了停车设施选择和出行路线的双层规划模型;张文会等[11]依据商业区和居住区不同停车时段的需求,建立了双目标分配模型。
已有研究成果考虑了影响城市停车的各种因素,提出了路侧停车泊位效率提升的方法,建立了基于商业区和居住区的停车供给模型,但未针对城市建成区路侧停车需求进行研究。路侧停车泊位设置后,路网通行能力变化的研究也较少。因此,笔者从求解路侧停车泊位需求角度出发,在确定路侧停车泊位需求后,提出一种以路网通行能力最大为目标的模型,为城市道路合理设置路侧停车泊位提供参考。
1 问题描述与建模
1.1 问题描述
随着汽车保有量的增加,城市车辆停放问题日益突出,合理设置路侧停车泊位可有效提升城市建成区停车供给能力,可实现动静态交通的和谐统一。如何合理设置路侧泊位成为亟需解决的问题。笔者研究城市建成区路侧停车泊位优化问题,主要体现在两个方面:①目前关于停车需求的预测主要针对区域内所需的全部数量,未对路侧停车需求的求解提出具有较强实用性的方法,如何计算路侧停车泊位需求成为亟需解决的问题;②如何在现有城市路网的基础上,合理地规划路侧停车泊位,减少对交通网络的影响,使得路网通行能力达到最大。基于以上问题,笔者求解区域路侧停车泊位需求量,并选取道路优先级指标作为权重系数,通过设置路侧停车泊位对道路通行能力变化函数建模,研究城市路侧停车泊位设置方法。
1.2 模型假设
模型作以下假设:①非机动车设有专用通道且灵活性大,不考虑非机动车对模型的影响;②不考虑研究区域之外停车现状对模型的影响;③城市主干道和次干道不设置路侧停车泊位,泊位均设置在城市道路支路上。
1.3 模型建立
笔者将停车场分为固定停车场、开放停车场和路侧停车场三类。住宅区、医院、学校以及其他不对外开放停车场定义为固定停车场;商业区和一些对外营业停车场定义为开放停车场;路侧停车场是指占用一部分用于车辆行驶的道路空间,为出行者提供一种快捷方便的停车方式。首先对研究区域的停车现状进行调查,通过调查数据分析区域内固定停车场和开放停车场是否满足现有停车需求,若满足,则不需进行优化,若不满足,则计算出需要设置路侧停车泊位需求量;然后通过道路优先级模型,确定符合设置路侧停车泊位路段,并给出道路优先级,优先级越高表示设置泊位的可能性越大;最后,基于笔者所建立的路网通行能力模型,得出规划方案,工作流程如图1。

图1 工作流程Fig. 1 Workflow
1.3.1 路侧泊位需求
研究区域内停车场泊位需求总量由固定停车场、开放停车场和路侧停车场三部分构成,计算公式为:
C=C1+C2+C3
(1)
式中:C为停车场泊位需求总量,辆;C1为固定停车场泊位需求数量,辆;C2为开放停车场泊位需求数量,辆;C3为路侧停车场泊位需求数量,辆。
通过调查开放停车场和路侧停车场泊位现状,得到停车总量N。为最大程度减少对道路通行的影响,计算出开放停车场可容纳最大车辆数N1。基于以上两个条件,计算出路侧停车场泊位需求数量,计算公式如式(2):
(2)
开放停车场可容纳最大车辆数N1计算公式如式(3):
(3)
式中:ε为开放停车场利用率;φ为开放停车场周转率,即医院、商业餐饮娱乐、旅馆、影剧院会议中心、博物馆图书馆展览馆、体育场馆和学校共7种用地类型的停车场周转率;k为修正系数。根据GB 50220—95《城市道路交通规划设计规范》[12],城市中心停车场k取1.1~1.3,其他地区取k=1。
针对不同的用地类型,应选取相应的停车周转率,笔者列举了城市用地的7种类型,如表1。

表1 7种用地类型的停车周转率Table 1 Parking turnovers for seven land types
1.3.2 道路优先级模型
笔者基于道路通行条件、车行道路路面实际宽度和机动车高峰小时交通量与基本通行能力之比v/c共3个条件(表2),增加了停车泊位与周边居民区的距离和道路长度两个条件,建立路侧停车约束模型,可得到设置路侧停车泊位道路优先级。
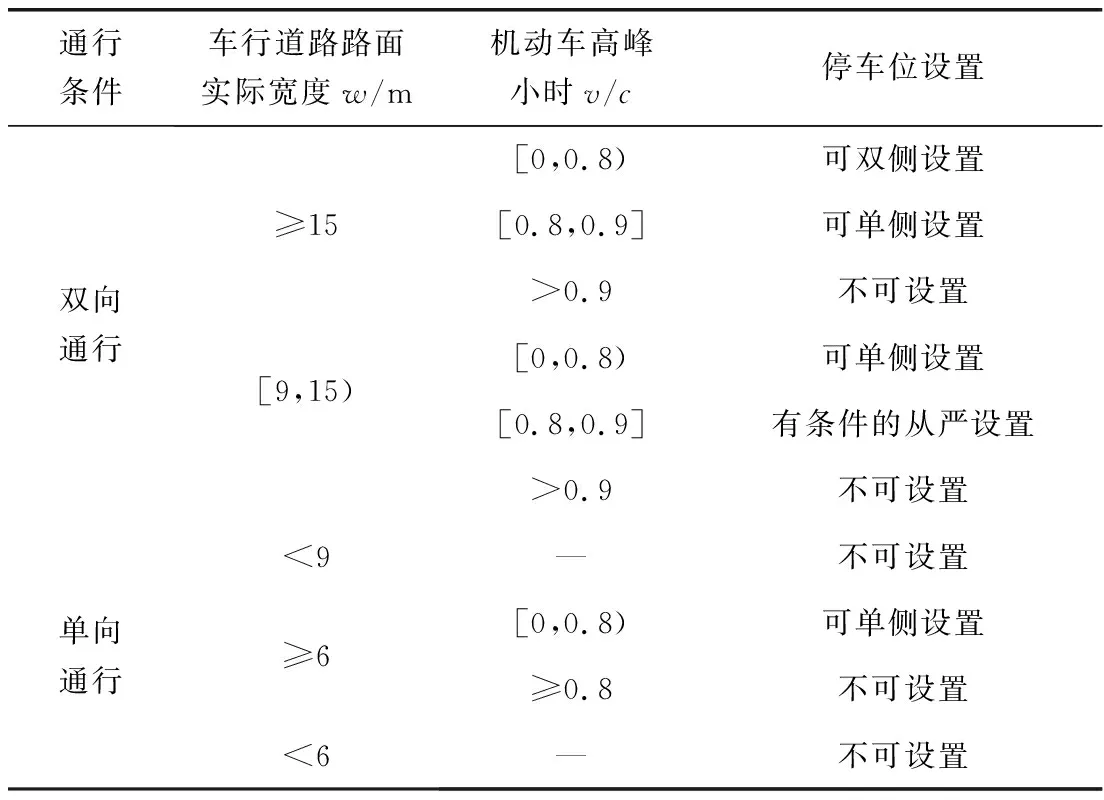
表2 设置路侧停车位的道路条件Table 2 Road conditions for setting roadside parking spaces
基于表2,道路优先级模型目标函数如式(4),约束条件如式(5)~式(12):
(4)
w≥15,0 (5) w≥15,0.8 (6) 9≤w<15,0 (7) 9≤w<15,0.8 (8) w≥6,0 (9) 0 (10) L>500,di=0.8 (11) (12) 式中:W表示规划区域内各路段设置停车泊位的优先级;式(5)~式(8)为双向通行车道参数;式(9)表示单向通行车道参数;L为距周边居民区距离(居民区一般指在城市较为集中的居住地,且具有一定规模,满足居民区的还应有相关配套设施,比如学校、医院、市场等);ti为道路长度与交通量乘积的占比;li为各条道路的长度;vi表示各条道路的交通量。 1.3.3 路网道路通行能力模型 道路通行能力是指在正常的道路、交通、管制以及运行质量要求下,单位时间内道路设施在某点或某断面处通过的最大车辆数。城市路网由多条不同的道路交互连接组成,而每条道路由多条不同的路段组成。为了能够全面合理地评价城市路网运行状况,笔者将道路优先级作为权重系数,结合在路侧设置停车位后通行能力函数〔式(13)〕,建立路网通行能力模型如式(14),约束条件如式(15)~式(17): (13) (14) (15) (16) (17) 式中:xa为设置路侧停车泊位数;Ci,max为道路最大通行能力,即未设置路侧停车带的道路通行能力,pcu/h;Ci,min为道路最小通行能力,即泊位数为xi,max时的道路通行能力,pcu/h;xi为路段i设置的泊位数,个;xi,max为路段可设置的最大泊位数,个;ζ为相当小的参数,建议取0.001;di为路段的车道宽度,城市道路宽度为3.75 m;γ为停车位宽度与道路通行宽度的调整系数,建议取0.5。 路侧停车优化的求解分为3个阶段。第一阶段为研究区域内现状停车调查并求解路侧停车需求量;第二阶段为确定道路优先级;第三阶段为求解非线性有约束的区域路网通行能力最大时路侧停车泊位量。笔者采用的算法为fmincon函数中的序列二次规划法,在每一步迭代中求解二次规划子问题,并用BFGS法更新拉格朗日Hessian矩阵,得出最优解,为决策者提供最终的规划方案。迭代及计算进程如图2。 图2 模型求解流程Fig. 2 Flow chart of model solution Step 1数据采集。对研究区域停车现状进行调查,主要采集停车场利用率、停车场周转率、停车场容量和区域内道路信息。 Step 2将研究区域数据整理归类,得到研究区域内是否需要设置路侧泊位。 Step 3通过道路优先级模型,得到研究区域内可设置路侧停车泊位路段及道路优先级。 Step 4利用路网通行能力模型,初始化参数,按照模型约束条件得到初始可行解x0。 Step 5调用fmincon函数,若算法终止,则计算结束,否则转入下一判定条件。 Step 6重复Step 4~Step 5,直至算法终止,得出最优解。 以昆明市盘龙区东华街道为例,街道西以环城东路为界,东以金汁河及迎溪村实际管辖线、蒋家营村实际管辖线为界,南以人民东路为界,北以穿金路为界,路网信息如图3。 图3 区域路网Fig. 3 Regional road map 通过对昆明市盘龙区东华街道停车现状调查,得到东华街道日均停车需求量为10 000次。本区域范围内共有开放停车场29个,累计可提供泊位数为4 050个。根据区域地理位置,停车场利用率ε=0.7,泊位周转率φ=3.0,修正系数k=1.1。依据式(1)~式(3),得到每日开放停车场可容纳最大车辆停放数为7 732次,因此须提供日均路侧泊位需求量为2 268次。考虑停车场利用率、泊位周转率和修正系数3个参数后,经计算得到,路侧泊位设置数为1 188个。 依据城市主干道和次干道不设置路侧泊位的原则及实地调查,可得出延安医院附近可提供路侧泊位的道路有17条,按照小龙路、中营路、文艺路、田园路、东华东路、东华路、春登街、源文路、知春街、新宁巷、文汇巷、稻香巷、小龙巷、新安巷、连环路、新龙巷、新安里顺序依次编号为1~17。依据道路优先级模型,v/c分别取最大服务交通量、高峰小时交通量、年平均日交通量与基本通行能力之比;常规设置方法即道路交通量与路侧停车泊位成反比,交通量最小的路段设置满以后,依次设置次小路段,直至达到区域路侧泊位需求量为止。按照以上4种分类,可得到不同的权重系数,如图4。 图4 权重系数Fig. 4 Weight coefficient 通过3.1节和3.2节得到可设置路侧泊位的路段及道路基本条件,由CJJ 37—2012《城市道路工程设计规范》[13]可知,行车速度为30 km/h时,单车道通行能力为1 600 pcu/h。通过道路优先级模型〔式(4)〕计算可得泊位设置方案如表3。 表3 路侧停车泊位设置Table 3 Berth setting for roadside parking 依据最大服务交通量与基本通行能力之比,设置路侧泊位后道路通行能力变化如图5。 图5 通行能力变化Fig. 5 Traffic capacity variation 由路网通行能力模型〔式(14)〕可得出,常规设置方法和基于改进路网通行能力设置方法的路网通行能力分别为28 031、29 947、29 845、30 127 pcu/h。与常规设置方案对比,基于改进路网通行能力设置方法的路网通行能力分别提高了6.84%、6.47%和7.47%。趋于最优解过程如图6。 图6 趋于最优解过程Fig. 6 Tending to an optimal solution 为验证路网通行能力模型〔 式(14)〕可行性,利用交通仿真软件VISSIM在平峰交通量和高峰交通量条件下对研究区域路网进行交通仿真。分别对比未设置路侧泊位、常规设置路侧泊位和基于改进路网通行能力设置路侧泊位3种交通延误,选用总停车延误、停车次数、车均延误、总延误时间和总行程时间5个指标分析模型可行性。与常规路侧泊位设置方法对比,基于改进路网通行能力设置方法,在平峰交通量和高峰交通量条件下,总停车延误分别减少68.75%和19.68%;停车次数分别减少52.56%和28.04%;车均延误分别减少36.31%和12.01%;总延误时间分别减少35.36%和16.69%;总行程时间分别减少14.28%和12.89%。研究结果表明,不同交通量条件下,各指标变化率不同,但各项指标均有减少,显著提升了路网的整体通行效率,对改善道路交通条件有明显作用, 结果如表4。 表4 平峰、高峰交通量3种方式下交通延误对比Table 4 Comparison of traffic delay under three modes of flat-peak traffic volume and peak traffic volume 笔者研究了城市建成区路侧规划方法,得到了研究区域内路侧泊位需求数量;基于路网通行能力最大的条件下,提出一种新的路侧泊位规划模型。研究结果表明,笔者所提模型优化了区域内路侧泊位设置,提高了路网整体通行效率,验证了模型的可行性。需要指出的是,笔者没有考虑规划区域之外的停车需求对路侧泊位的影响,未来将进一步研究各区域之间相互影响程度,完善路侧泊位规划方法。2 算法设计

3 算例与仿真

3.1 泊位需求计算
3.2 道路优先级划分

3.3 路网通行能力计算
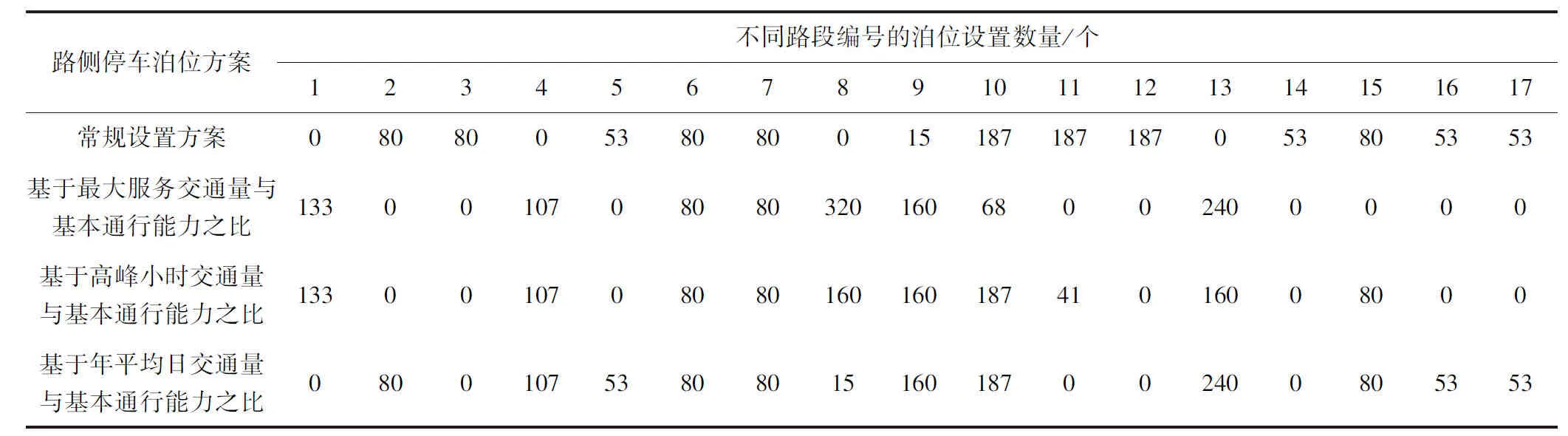

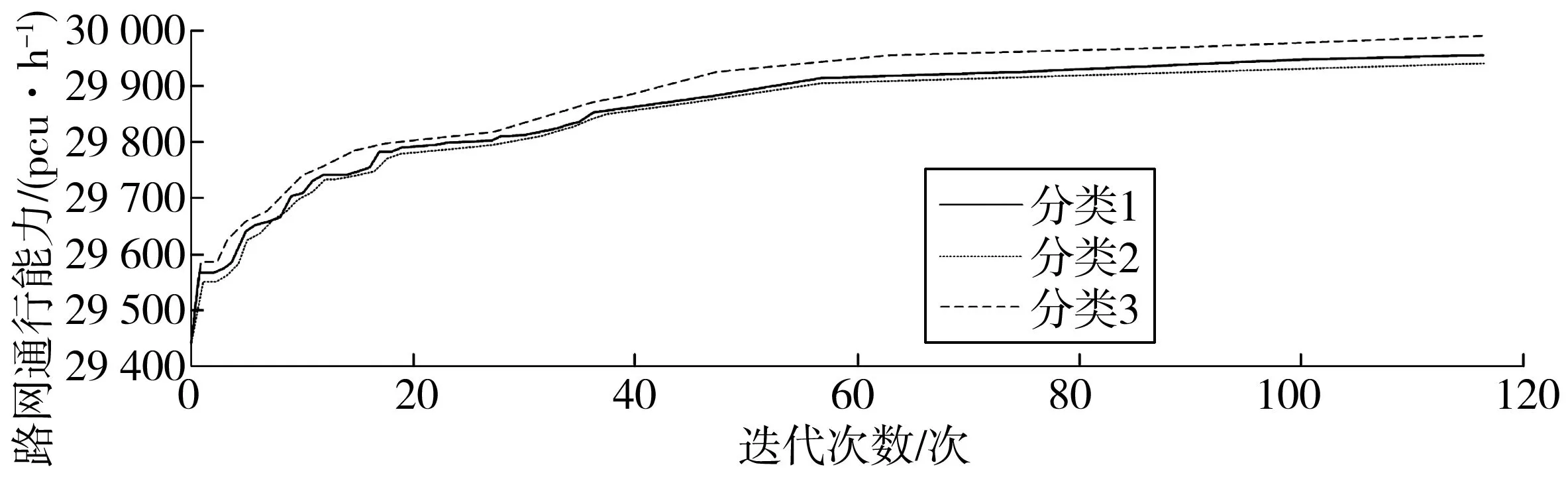
3.4 路网通行能力模型仿真验证
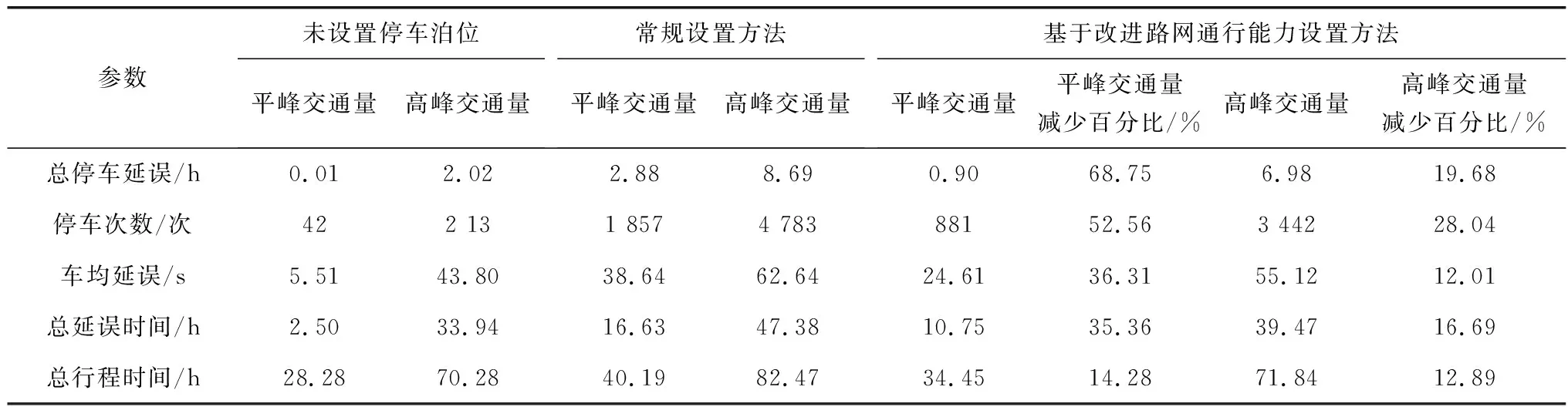
4 结 语

