大跨度连拱隧道下穿古建筑物的安全评估

郭佳嘉，张国浩，褚 存,3,4

(1. 中交第二航务工程局有限公司，湖北 武汉 430040； 2. 中交第二航务工程局第四工程有限公司，安徽 芜湖 241000；3. 长大桥梁建设施工技术交通行业重点实验室，湖北 武汉 430040；4. 武汉大学 水资源与水电工程科学国家重点实验室，湖北 武汉 430072)

0 引 言

我国古建筑物具有分布广泛、历史悠久、文化底蕴深厚等特点，但古建筑物往往年代久远，自身材料及结构已受到不同程度损坏，材料强度和稳定性均较差。当修建的隧道需要下穿古建筑物时，会给文物保护和施工带来了巨大困难。因此在施工中，若隧道要下穿古建筑物保护区时，就需要对古建筑物安全性及施工方案可行性进行研究和评估，以达到既能保护建筑物又能保障施工安全、节省工程造价、降低施工工期的目的。

针对隧道下穿古建筑物的问题，学界展开了相关的研究。李二兵等[1]采用监控量测手段对南京市九华山隧道下穿古城墙的变形特点及控制措施进行了分析；何满潮等[2-3]基于现场调研和工程地质勘察，使用FLAC3D仿真软件对高句丽将军坟的变形破坏内在机理和布达拉宫西印经院地基应力特征与结构变形进行了分析；谢雄耀等[4]对盾构隧道下穿老旧建筑物群的微沉降控制技术进行了研究；程红战等[5]对考虑参数空间变异性的隧道下穿建筑物安全性进行了研究与评估；李永宽等[6]对浅埋暗挖隧道下穿地表建筑物的安全控制技术进行了分析。

笔者依托实际工程项目，对浅埋偏压条件下大跨度连拱隧道下穿古炮台遗址的地表沉降进行了分析，对古建筑物的安全性进行了评估[7-10]。

1 工程概况

南京仙新路过江通道工程是南京市新建的一条重要过江通道，包括跨江主桥、引桥、乌龙山隧道等。其中：乌龙山隧道长247 m，为双向六车道连拱浅埋短隧道，最大埋深仅30 m。

乌龙山隧道地貌主要为构造剥蚀残丘区，地面高程15～77 m不等，覆盖层表层为素填土、种植土，工程性质较差，种植土以粉质黏土为主，填土主要为可塑-硬塑状粉质黏土，厚度为5～35 m；隧道下伏基岩主要为强风化角砾岩，岩体基本质量等级为Ⅴ级。乌龙山隧道大部从可塑-硬塑状中上更新统粉质黏土中穿过，总体围岩级别以Ⅴ级为主，在隧道洞口区域为Ⅵ级。

隧道正洞开挖断面最大跨度为15.8 m，高度为10.32 m，中导洞开挖断面最大跨度为5.1 m，高度为7.5 m。隧道洞身采用新奥法原理进行设计，采用钢拱架，喷射混凝土，砂浆锚杆组成初期支护来充分发挥围岩的自稳能力，超前大管棚加超前小导管的双层预加固措施为主要的沉降控制手段，隧道支护参数如图1。该隧道下穿乌龙山炮台遗址保护区，必须要保证炮台遗址不会因地表沉降过大而发生损坏和开裂，因此应对隧道下穿古炮台遗址的地表变形情况进行分析，对古建筑物安全性进行评估。

图1 连拱隧道三导洞法开挖支护设计参数Fig. 1 Design parameters of excavation and support of three heading method in multi-arch tunnel

2 数值计算

2.1 建立模型

为了建立能够真实反映现场地形状况的三维计算模型，笔者采用CFD方法进行建模[11]。即通过提取乌龙山炮台遗址附近的等高线数据，导入第三方建模软件来生成精细化三维地质模型，然后建立隧道结构和计算分组，划分网格后导入FLAC3D仿真软件进行计算。为了适应模型复杂的边界条件，单元网格采用全四面体网格模型，同时加密隧道附近的网格数量来保证计算精度[12]，导入FLAC3D仿真软件后生成的有限差分计算模型和分组如图2。

图2 三维有限差分计算模型Fig. 2 Three-dimensional finite difference calculation model

2.2 数值模拟

为了模拟天然岩土体的固有沉降和初始地应力，需先求解模型初始地应力场。模型初始地应力场采用弹塑性求解，模型底部和四周边界固定，顶部自由，岩土体的计算采用Mohr弹塑性本构模型，挡土墙和导向墙采用线弹性模型，根据项目前期的地勘情况，相关计算参数如表1。

表1 岩土体的相关参数Table 1 Relevant parameters of rock and soil mass

模拟过程按照施工方案中的顺序进行，方案中隧道采用三导洞法开挖，中导洞先行施工，中导洞施工完成后进行中隔墙施工，然后再进行隧道正洞施工。正洞施工时先施工正洞的侧导洞，再用台阶法施工正洞剩余部分，连拱隧道施工顺序如图3。模型初始地应力场计算完成后，对塑性区、位移和速度进行归零处理。

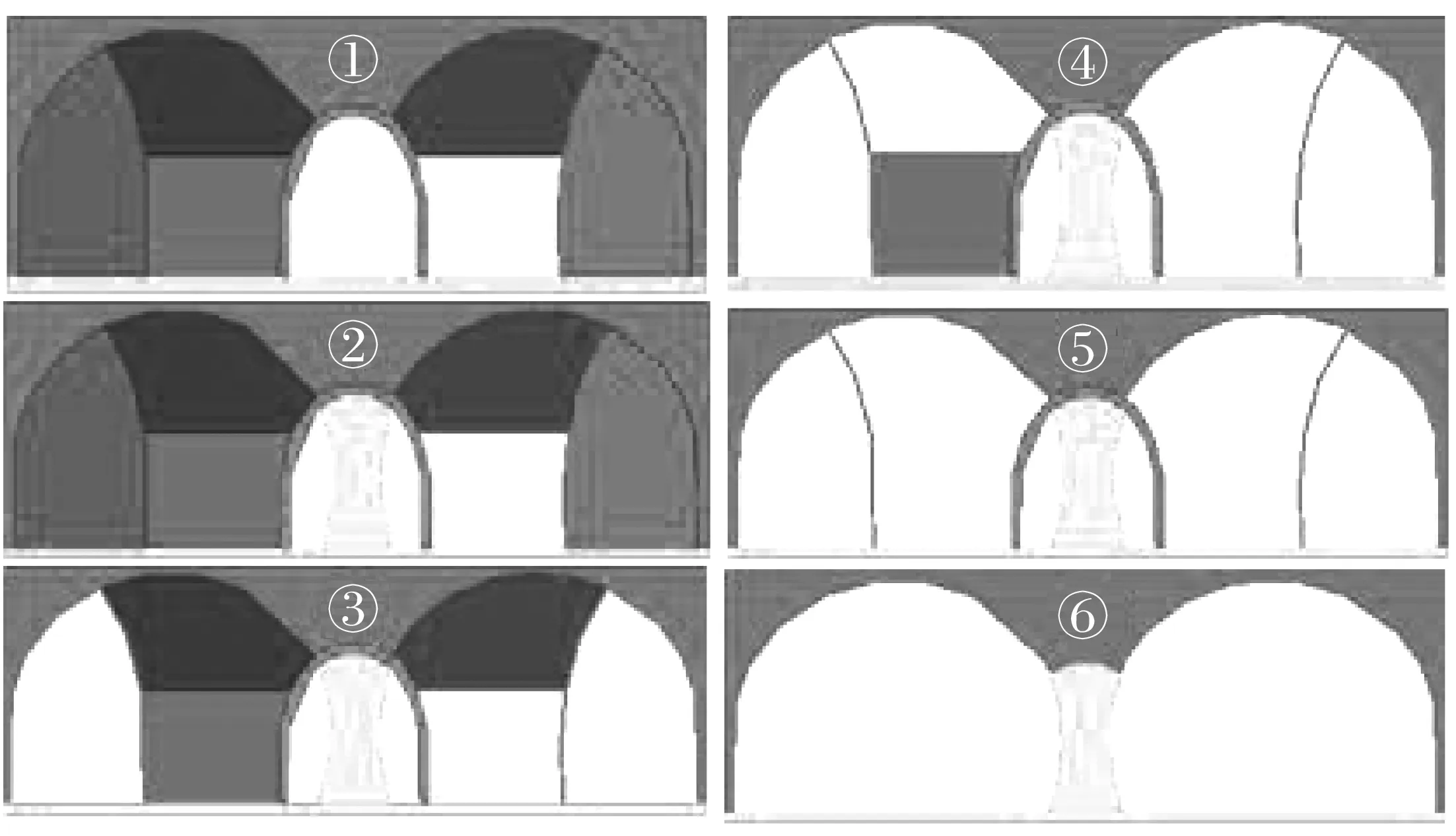
图3 连拱隧道施工顺序Fig. 3 Construction sequence of multi-arch tunnel

3 结果分析

笔者对中导洞开挖时的变形情况进行分析。中导洞按两台阶法进行开挖模拟，每循环进尺1.2 m，超前管棚、超前小导管、锚杆及衬砌采用FLAC3D仿真软件自带的Pile、Cable、Shell结构单元进行模拟，通过FISH编写程序自动进行开挖循环计算，计算完成后的围岩垂向位移云图和塑性区分布如图4、图5。

图4 围岩垂向位移云图(单位：m)Fig. 4 Nephogram of vertical displacement of surrounding rock

图5 围岩塑性区分布图Fig. 5 Distribution map of surrounding rock plastic zone

从图4、图5可知：在中导洞贯通后，中导洞的顶拱沉降最大约为1.2 cm，地表累计沉降量值范围为2.1～2.6 mm，古炮台整体变形最大为0.23 mm；且古炮台及附近区域的塑性区并未出现，说明该区域处于弹性变形范围内，中导洞的开挖对地表沉降影响很小，对古炮台的稳定性影响极小。

中导洞开挖完成后紧接着进行中隔墙施工，最后进行隧道正洞施工。正洞按施工方案进行仿真模拟，先进行侧导洞施工，然后进行正洞开挖。隧道正洞采用台阶法施工，采用超前管棚加超前小导管进行预支护，先进行正洞上台阶开挖，之后及时对正洞上台阶进行初期支护，再对正洞下台阶进行开挖，左、右洞采取相同的施工步序，两洞在纵向上距离为30 m。开挖模拟完成后的垂直位移云图、水平位移云图、最大主应力云图和塑性区分布如图6～图8。

图6 开挖完成后地表位移云图(单位：m)Fig. 6 Nephogram of surface displacement after excavation

图7 开挖完成后最大主应力云图(单位：Pa)Fig. 7 Nephogram of maximum principal stress after excavation

图8 开挖完成后围岩塑性区分布Fig. 8 Distribution of surrounding rock plastic zone after excavation

由图6(a)可看出：在隧道开挖贯通之后，地表沉降量值分布范围为0.1～2.3 cm，受下穿隧道开挖影响，地表沉降量值在中间区域最大并向两侧递减，其中古炮台位于地表沉降变形最大区域，炮台的最大沉降量值达到了2.1 cm。从图6(b)可知：隧道开挖完成后引起的地表水平位移量很小，约为0.12～1.30 cm，地表水平位移表现出中部小，周围大的特点，其中古炮台的最大水平位移约0.3 cm，可见古炮台变形以沉降变形为主。

由图7可知：当隧道开挖完成后，古炮台顶部主要承受拉应力、下部承受压应力，其中炮台顶部的最大拉应力约为0.16 MPa，底部的最大压应力约0.38 MPa。

由图8可知：古炮台未有塑性区出现，可见是发生的弹性变形。因此笔者根据隧道开挖完成后古炮台的沉降变形、水平变形、最大主应力和塑性区分布来看，可认为该隧道的支护设计参数和下穿施工方案合理可行，隧道的开挖不会让古炮台产生过大的变形从而造成其灾难性损坏。笔者建议在实际施工中应加强监控量测，古炮台最大沉降量值以2 cm为控制标准。

4 结 论

笔者通过对大跨度连拱隧道下穿古建筑物的数值模拟，可得出以下结论：

1)在隧道施工过程中，中导洞开挖跨度和开挖断面均较小，因此其自成拱的能力和掌子面的自稳能力均较强，中导洞开挖对地表扰动很小，中导洞施工过程对古建筑物影响极小。

2)隧道正洞的开挖贯通主要对古炮台沉降变形影响较大、水平变形影响较小，开挖引起的地表沉降变形规律为中部区域最大，并向周围递减；地表水平变形规律为中部最小，周围区域较大。

3)该隧道工程采用的支护设计参数及施工方案对地表沉降控制效果较好，隧道下穿造成的古炮台最大沉降量约为2.1 cm，水平变形量约为0.3 cm，古炮台未有塑性区出现，整体处于弹性变形，隧道施工下穿不会对古建筑物产生严重损坏。