基于自耦PID的三连杆机械臂轨迹跟踪控制
陈丽秋, 曾喆昭
长沙理工大学,长沙 410114
0 引 言
近20余年来,随着人工智能的发展和高难度、高风险作业环境的需要,多连杆机械臂系统在许多工业和航空航天领域获得了广泛应用[1-3].然而,由于多连杆机械臂系统是一种多输入多输出、强耦合的非线性系统[4],且存在复杂内部未知动态和外部干扰,因而实现其关节轨迹跟踪控制存在一定的难度.目前,针对这一问题,国内外学者提出了多种控制方法,并取得了许多有效的研究成果,如:PID(proportional-integration-differential)控制[5-7]、自适应神经网络控制[8-10]、自抗扰控制[11-12]以及滑模控制[13-16]等,其中,PID控制结构简单,不依赖于具体的系统模型,却存在增益鲁棒性差与抗扰动鲁棒性差的局限性,为此,文献[6-7]提出了改进的PID算法,尽管能有效解决传统PID的局限性问题,但也增加了控制系统的复杂程度;自适应神经网络控制ANNC (adaptive neural network control)可以在线估计补偿系统内部不确定因素以及外部干扰,进而提高控制系统的抗扰动鲁棒性,然而该方法存在结构复杂、参数较多、计算量较大的局限性;自抗扰控制ADRC (auto disturbance rejection control)则涉及一些非线性不光滑函数的复杂计算,导致了闭环控制系统稳定性分析的难度;滑模控制SMC (sliding mode control)不依赖于被控对象模型,且具有较好的增益鲁棒性与抗扰动鲁棒性,然而因涉及符号函数的等速趋近率,所以存在高频抖振现象,不利于执行机构.此外,文献[17]通过设计估计器实现对系统内部未知动态以及外部干扰的估计补偿,进而实现机械臂各关节的控制,却增加了控制系统的复杂性;文献[18]通过设计自适应鲁棒控制算法实现对系统不确定干扰和建模误差的补偿,但该方法依赖于被控系统的模型信息,且涉及参数较多.
为解决上述控制方法存在的局限性问题,拟使用文献[19-20]提出的自耦PID,即ACPID(auto-coupling proportional-integration-differential)控制方法,该方法包括ACPI(auto-coupling proportional-integration)和ACPD(auto-coupling proportional-differential),通过一个速度因子将比例、积分和微分3个不同属性的物理环节紧密耦合为量纲相同的整体,进而实现3个环节功能各异、目标一致的协同控制,不仅纠正了传统PID控制系统的量纲冲突问题,而且避免了比例作用力、积分作用力以及微分作用力独自工作的不协调控制,解决了传统PID增益鲁棒性差与抗扰动鲁棒性差的问题,且控制器结构简单,便于实际应用.
借鉴ACPID控制思想来解决三连杆机械臂轨迹的跟踪控制问题,根据文献[21]中提出的总和扰动思想,三连杆机械臂各关节已知或未知动态和外部扰动等复杂因素分别定义为3个总扰动,进而将各关节非线性系统映射为未知线性系统,并构建了受控误差系统,在忽略积分作用的情况下,分别设计了各关节的ACPD子控制器,进而实现各关节的独立跟踪控制;采用基于误差变化率的自适应速度因子,在保证快的动态响应速度同时,也可以保证高的稳态控制精度与强的抗扰动能力;不仅为机械臂轨迹的跟踪控制提供一种有效的应用案例,而且也进一步验证ACPD控制方法的有效性.
1 问题描述
三连杆机械臂结构如图1所示.

图1 三连杆机械臂结构图Fig.1 Structure chart of three-link manipulator
其中,mj为连杆j的质量,lj为第j连杆的长度,Ij为第j关节的转动惯量,rj为第j连杆质心到转动关节的距离,qj为第j关节的关节变量.
考虑到关节摩擦力和外部扰动的影响,三连杆机械臂的动力学模型[4]可以表示为

(1)

针对三连杆机械臂系统(1),建立3个通道分别对各关节进行控制,令第j(j=1,2,3)个连杆的控制力矩为第j关节的主要控制输入,其他连杆控制力矩作为第j关节的扰动,根据文献[21]中所提出的总扰动(或扩张状态)思想,将各关节已知或未知动态、外部扰动等复杂因素分别定义为3个总扰动w1、w2、w3,所谓的未知动态包括了模型不确定性与时变不确定性引起的未知动态,则系统(1)可以等价映射为线性扰动系统
(2)
其中,
由于系统(2)是系统(1)的等价映射,因而设置有效的控制器控制系统(2)即可有效控制系统(1).
2 ACPID控制器
2.1 三连杆机械臂轨迹的ACPD控制器设计
(3)
其中,uj为第j连杆的控制力矩,yj为第j关节的角度输出,b0j=1/hjj为第j关节的控制力矩系数.
由于3个通道均是基于ACPID控制方法设计控制器,且原理一致,故对3个通道控制器统一进行设计分析,如下:
设机械臂第j关节的期望轨迹为rj,则跟踪误差为ej1=rj-yj=rj-xj1,误差微分为
(4)
由式(3)~(4)可得机械臂第j关节的受控误差系统为
(5)

根据文献[19-20]提出的ACPID (包括ACPI、ACPD)控制思想,在忽略积分环节的情况下,设计三连杆机械臂第j关节的ACPD控制律为
(6)
其中,zjc>0是第j关节ACPD控制律的速度因子,量纲为s-1,j=1,2,3.
根据ACPD控制律(6), 则系统(1)或(2)的控制原理框图如图2所示.

图2 三连杆机械臂系统ACPD控制原理框图Fig 2 Three-link manipulator system ACPD control schematic
2.2 闭环控制系统分析
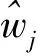
证明. 将ACPD控制律(6)代入受控误差系统(5),可得第j关节的ACPD控制子系统为
(7)

对受控误差子系统(7)取单边拉普拉斯变换,得
(8)
整理可得
(9)
定义系统(8)的传输函数为
(10)
由式(10)可知, 当0 由式(10)可得第j关节控制子系统单位冲激响应hj(t)为 hj(t)=te-zjct,t>0 (11) (12) 考虑到任何实际控制系统都是输入受限系统,因此,控制输入存在一定的约束条件,满足 (13) 其中,ujm为机械臂第j关节控制输入的最大幅值. 为验证各关节ACPD控制力限幅的合理性,现给出其受限时的稳定性定理及证明. 定理2.当速度因子0 (14) 对其进行单边拉普拉斯变换整理可得 (15) 由此可定义第j关节控制力受限下的系统传输函数为 (16) 令Aj(s)=s2+2λjzjcs+λjzjc2,根据劳斯判据,系统(16)稳定的充要条件为Aj(s)劳斯阵列表的第一列元素全部正定,其中,Aj(s)的劳斯阵列第一列存在3个元素,分别为 (17) 由式(17)可得,当0 zjc=zjcmexp(-βj|ej2|) (18) 其中,zjcm=20αj/Tjr是第j关节ACPD控制律的最大速度因子,1<αj≤10为常数,βj=1+0.3αj是衰减因子,Tjr是第j关节ACPD子控制系统由动态过程进入稳态过程的过渡过程时间. 为了验证本控制方法的有效性,以文献[18]中的机械臂模型参数为例进行仿真实验,其结构如图1所示,其具体模型参数如表1所示. 表1 三连杆机械臂模型参数Tab.1 Parameter values of three-link manipulator 三连杆机械臂动力学模型中的元素具体如下: b1=(m2r2+m3l2)g,b2=m3r3g, h11=I1+a1cos2(q2)+a2cos2(q2+q3)+ 2a3cosq2cos(q2+q3), h12=h21=h13=h31=0, h22=I2+a1+a2+2a3cosq3, h23=h32=a2+a3cosq3,h33=I3+a2, g2=b1cos(q2)+b2cos(q2+q3), g3=b2cos(q2+q3), μ1=μ2=μ3=5 N·m为相关库仑摩擦力矩大小. 令机械臂各关节的初始状态、外部干扰、期望轨迹以及最大输入幅值分别为 2)外部干扰:d1=0.1sin(t),d2=0.1cos(0.5t),d3=0.1sin(t/3); 3)期望轨迹:r1=1.5sin(0.04πt), r2=1.5cos(0.04πt),r3=1.5sin(0.04πt); 4)最大输入幅值:u1m=150 N·m,u2m=700 N·m,u3m=300 N·m. 下列实验中,三连杆机械臂3个关节的ACPD控制器分别如下: (19) 令T1r=T2r=T3r=1,α1=α2=α3,机械臂各关节的速度因子取值如表2所示,仿真时间100 s,仿真步长0.001 s,本控制方法的仿真结果如图3所示. 表2 各关节自适应速度因子值Tab.2 Adaptive speed factor for each joint 图3 机械臂三关节位置跟踪效果图Fig.3 Position tracking results of three joints for manipulator 由图3可以看出,当αj=5或αj=10时,三连杆机械臂3个关节的位置跟踪响应速度都很快,不仅无超调、无振荡现象,而且控制信号光滑、稳态跟踪控制精度高;当αj=5时,分别在1.4 s、2.0 s及1.7 s左右即可跟踪期望轨迹,各关节的稳态误差绝对值分别小于1.5×10-4rad、1×10-3rad以及2×10-3rad;当αj=10时,分别在1.7 s、2.5 s及1.8 s左右即可跟踪期望轨迹,各关节的稳态误差绝对值分别小于4×10-5rad、2.5×10-4rad以及4×10-4rad,表明所使用的自适应速度因子具备较大的整定裕度,且均能取得良好的控制效果;文献[18]中3个关节的控制信号较为光滑,但位置跟踪响应速度较慢,期望轨迹与实际输出误差较大,且存在超调、振荡现象.因此,与文献[18]相比,本控制方法具有更快的响应速度和更高的控制精度. 针对三连杆机械臂轨迹跟踪控制问题,提出了一种基于 ACPID的控制方法,该方法将已知或未知动态和外部扰动等复杂因素分别定义为一个总扰动,在忽略积分环节的情况下,分别设计了各关节的ACPD子控制器,分析了各关节ACPD控制子系统是鲁棒稳定的,并且具有良好的抗扰动鲁棒性.仿真结果表明本文控制方法不仅响应速度快、控制精度高、抗扰动鲁棒性强,而且无超调与振荡现象.此外,ACPD控制器涉及参数只有速度因子zjc和控制系数b0j,控制器结构简单,便于实际工程应用,因而在机械臂轨迹跟踪控制领域具有重要的应用前景.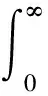


2.3 ACPD控制力限幅

2.4 自适应速度因子
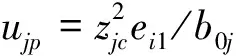
3 仿真实验与分析





4 结 论

