一种跳跃式再入鲁棒轨迹规划方法
韩铭麟,胡 军
北京控制工程研究所, 北京 100094
0 引 言
探月飞船等小升力体飞行器再入返回地球时,飞行工况复杂,任务安全需求高、技术指标高,一般采用跳跃式再入制导方式返回.跳跃式再入制导需要以标称返回轨迹为基准轨迹进行设计.标称返回轨迹的求解本质上是解一个最优控制问题.标称返回轨迹[1]设计中不仅要考虑强非线性的动力学约束,还要考虑复杂的过程约束,且很难用解析的方法获得最优解.目前标称轨迹规划方法主要分为两类:间接法和直接法[2].间接法利用变分法求解最优控制问题的一阶必要条件来获得飞行器的最优轨迹,其缺点是很难有效地处理不等式约束[3].直接法通过将控制或状态和控制变量离散化把最优控制问题转化为一个非线性规划问题,然后采用非线性规划方法求解此问题得到离散的最优轨迹点.常用的直接法包括打靶法、配点法和高斯伪谱法(全局配点法),其中高斯伪谱法具有更高的求解精度和更快的收敛速度[4].
高斯伪谱法[5]是一种全局轨迹规划方法,利用勒让德多项式逼近研究问题的轨迹,该方法能有效估计协态变量,且易于检验解的最优性.它的配点方式(中间稀疏,两侧密集)避免了龙格现象[6]的产生,具备用更少的配点获得更高求解精度的优势和以多项式时间收敛的特点.基于上述优点,高斯伪谱法在轨迹规划[7-9]设计中具有潜在的应用价值,引起了广大学者的研究兴趣.FAHROO在可重复使用运载火箭轨迹生成[10]研究中采用高斯伪谱法,该方法无需使用简化运动方程进行求解,在获得最优解的情况下还能保证求解精度.此后,FAHROO还研究了在突发控制故障和损坏情况下运载火箭的可重复回收问题[11],研究结果表明高斯伪谱法能有效地处理各种动力学模型、边界条件和过程约束以及表格数据.BOLLINO在上述研究基础上解决了可重复使用运载火箭再入6自由度弹道优化问题[12],而此前6自由度问题的求解一直被认为是非常困难的.上述基于伪谱法的飞行器轨迹规划研究均在给定初值情况下计算最优轨迹.然而对于载人登月飞船这类高速再入返回轨迹规划问题,再入初始点与标称设计可能存在很大差别,气动参数存在很大的不确定性.刘旭在载人探月飞船跳跃式再入轨迹设计中[13],利用状态初值单项拉偏仿真验证提出算法对参数变化的鲁棒性.PEI在在线再入轨迹设计中考虑了气动参数小范围不确定性对再入过程的影响[14].上述工作从不同方面研究再入轨迹规划方法的抗扰动能力,但仍然很难满足实际再入过程对参数变化具有鲁棒性的设计需求.
针对上述问题,提出一种基于分段高斯伪谱法的鲁棒轨迹规划方法.依据跳跃式再入的特点,推导了过载的微分方程,将过载约束转化为等式约束及状态量范围约束,得到新的增广再入模型,将原问题转化为新模型下的定点着陆问题进行求解.然后,在该模型的基础上,将动压约束和热流密度约束同样转化为等式约束及相应的状态量范围约束,建立扩展增广再入模型,并对新模型下的轨迹规划问题进行研究.最后,在初始状态偏差中考虑纵程偏差和横程偏差,验证在存在状态偏差及气动参数不确定性时提出方法的鲁棒性.仿真结果表明:提出的方法在上述条件下具备强鲁棒性,轨迹的动压、过载和热流密度约束满足设计需求,且精确规划到期望落点.
1 问题描述与定义
1.1 再入运动模型
3自由度再入运动[15]如下:
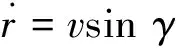
(1)
(2)
(3)
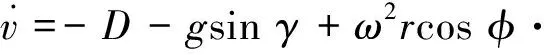
(4)
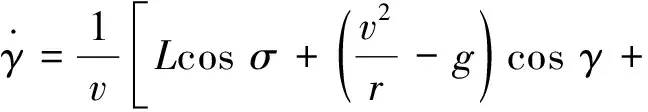
(5)
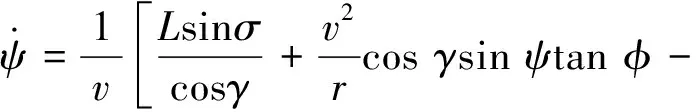
(6)
式中,r为飞船到地心距离,θ为经度,φ为纬度,ν为速度,γ为航迹倾角,ψ为航迹方位角,σ为倾侧角,ω为地球自转角速度,L为升力加速度,D为阻力加速度
(7)
式中,Sref为参考面积,CL为升力系数,CD为阻力系数,m为飞船质量.大气密度用ρ=ρ0e-h/hr表示,其中ρ0表示标准海平面大气密度,hr为基准高度.
飞行器再入过程中通常需要考虑如下动压、过载和驻点热流约束.
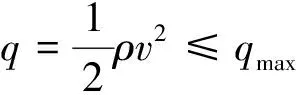
(8)
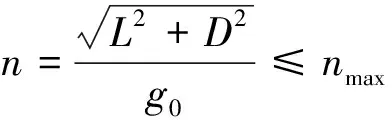
(9)

(10)
式中:Rn为驻点曲率半径;Vc为第一宇宙速度;C为经验系数[16],一般取1.1×105.
1.2 状态扩张
由于陀螺测量角速度的限制,将倾侧角速率作为扩张状态引入再入运动模型
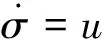
(11)

x=[r,θ,φ,v,γ,ψ,σ]
状态向量的初值约束和终值约束如下:
x(t0)=x0,x(tf)=xf
(12)
式中,x(t0)为再入点初值约束,x(tf)为落点终值约束.
1.3 最小落点偏差问题
考虑如下最小落点偏差优化指标:
J=rfarccos(cos(θend-θf)cos(φend)cos(φf)+
sin(φend)sin(φf))
(13)
式中,θf、φf分别为期望落点的经度和纬度,θend、φend分别为规划落点的经度和纬度,rf为落点地心距.该指标的物理含义是落点地心距下期望落点位置与规划落点位置的球面距离.
1.4 经典跳跃式再入模型问题描述
综上所述,给出经典跳跃式再入模型下的轨迹规划问题P0如下:
P0: min(13)
s.t. (1)-(12)
利用高斯伪谱法对问题P0进行求解,便可获得相应的跳跃式再入轨迹.
2 增广与扩展增广再入模型
2.1 经典再入跳跃式模型的缺陷
针对经典跳跃式再入模型下的轨迹规划问题P0,利用高斯伪谱法求解的再入轨迹对初始状态及气动参数变化敏感(即在特定参数下能得到满足动力学及过程约束的最优轨迹,微小的航迹倾角扰动会引起过载违反过载边界的情况发生,详细仿真实验及结果见5.1小节).
经过大量仿真研究经验的积累,发现将过载作为增广状态量引入到经典跳跃式再入模型,能有效地避免上述问题发生.
2.2 增广再入模型的建立
将式(7)代入式(9),得到过载的具体表达
(14)
式(14)两侧分别对时间求导,得
(15)
此时再入点的初始过载如下:
(16)
式中,h0为初始再入高度,v0为初始再入速度.由式(15)、(16)结合式(17)的过载边界约束重新定义了过载约束的形式.
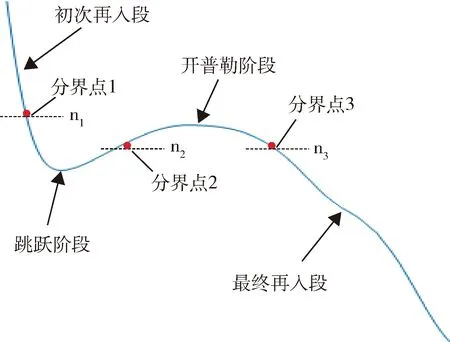
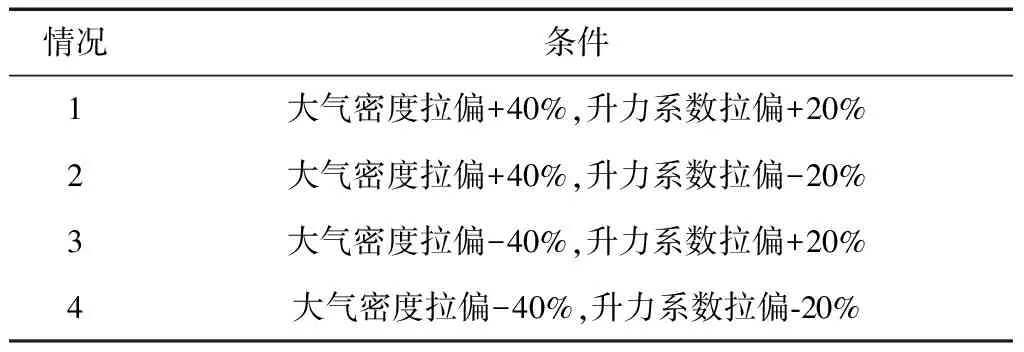
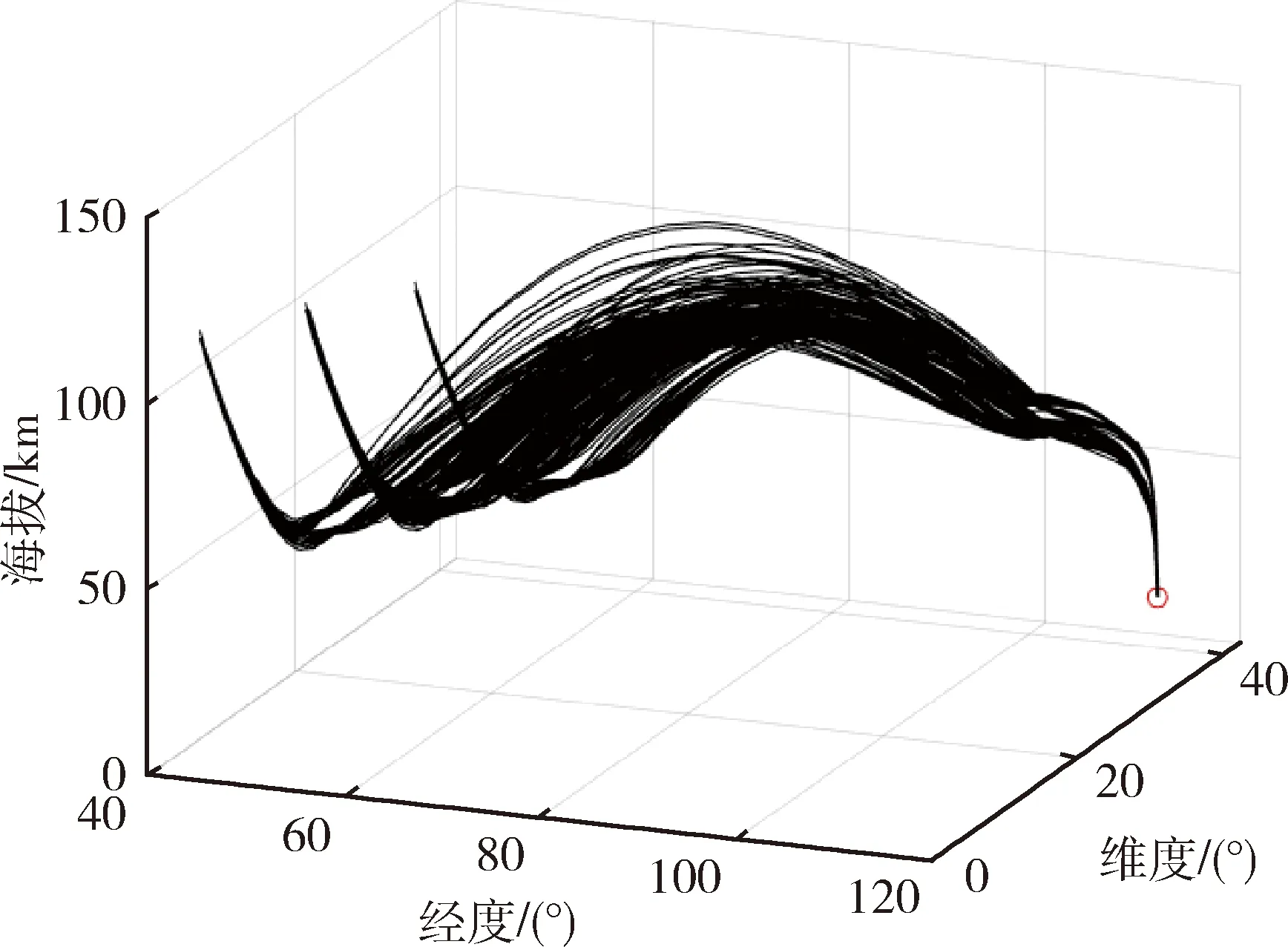
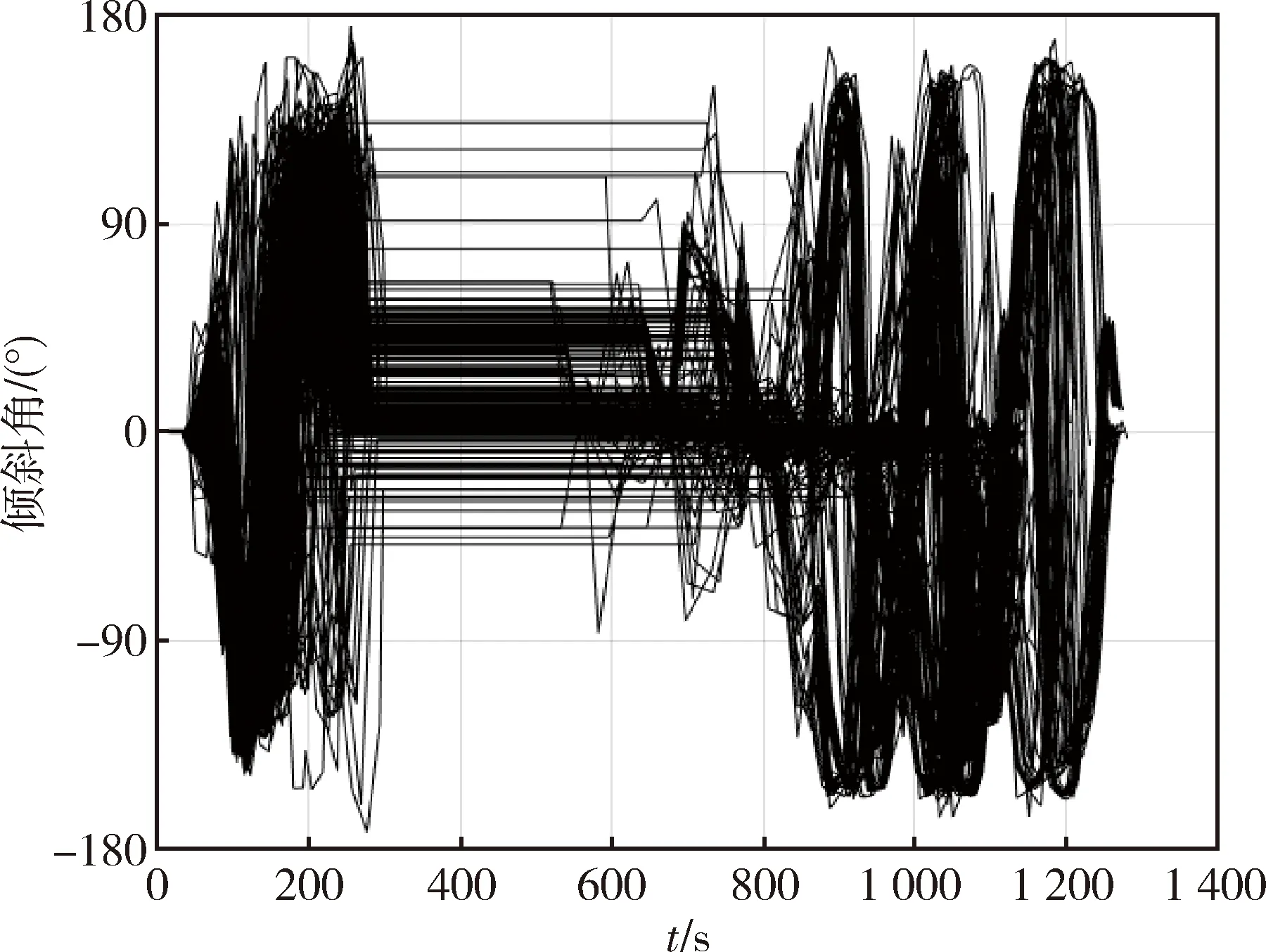
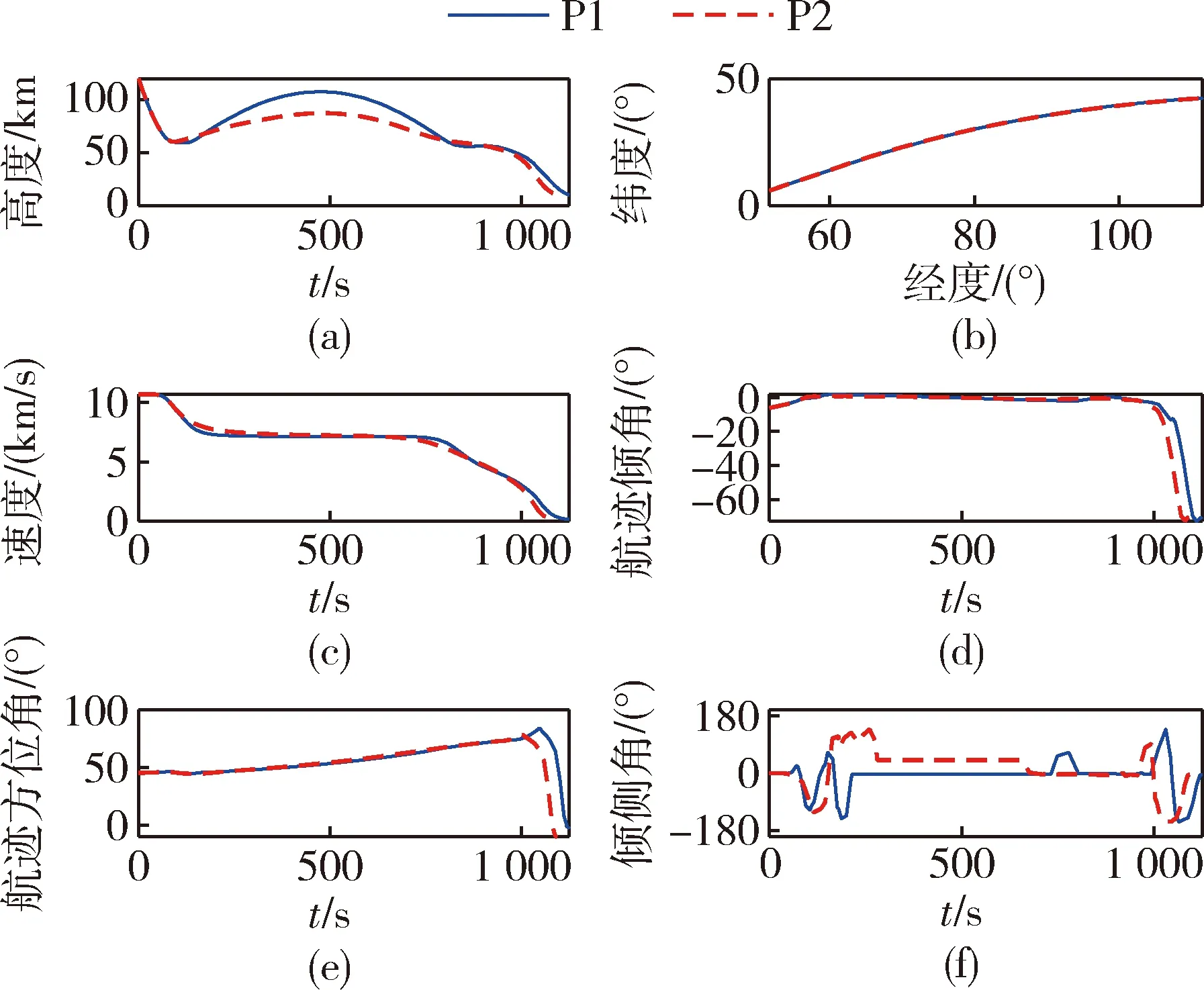
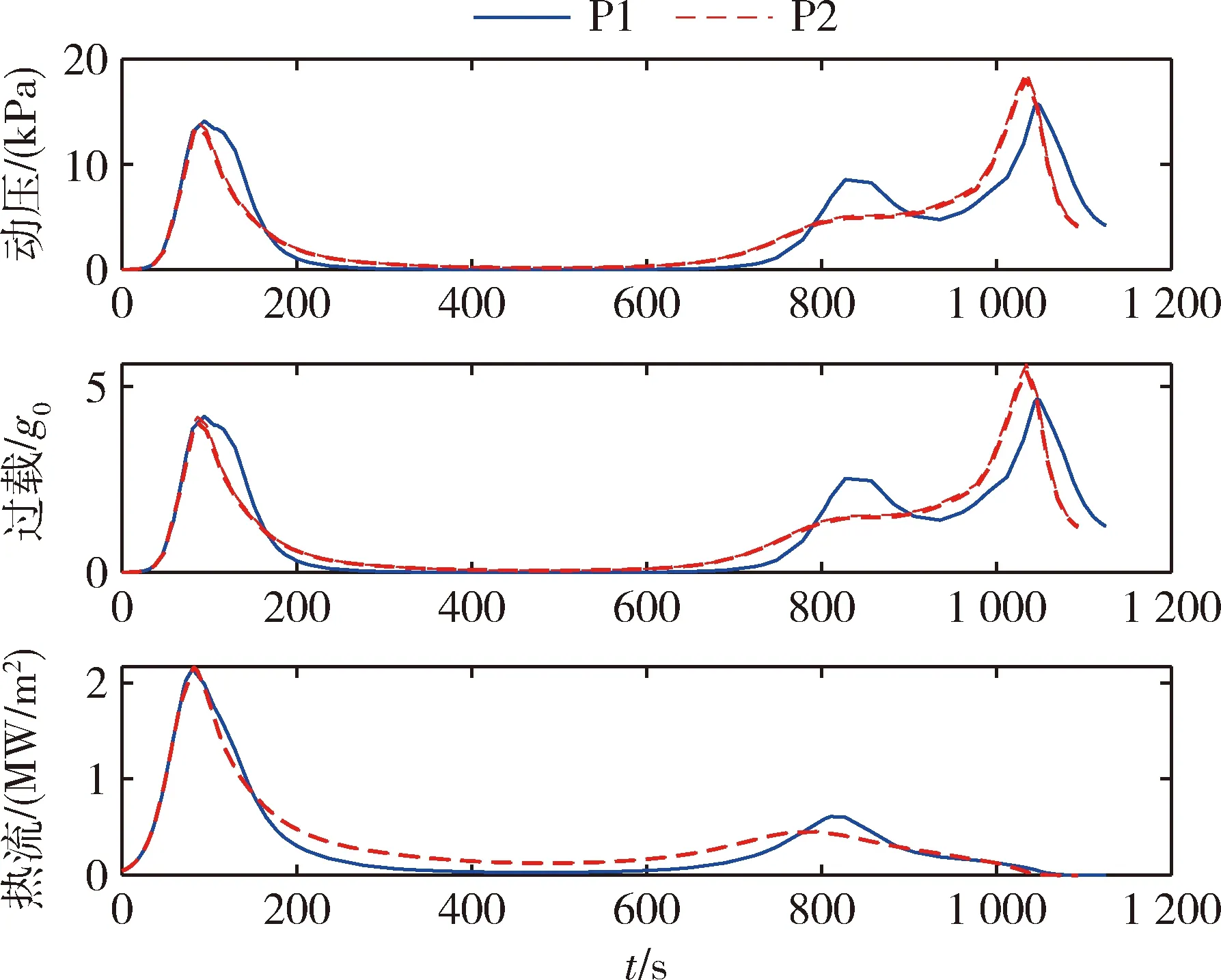
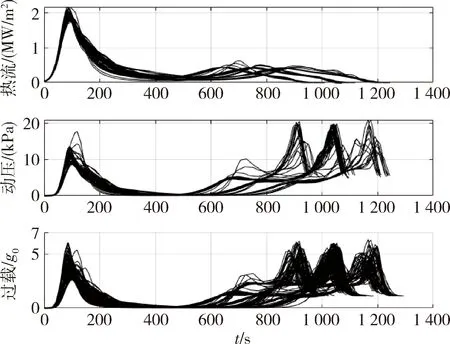
0 (17) 式(15)与跳跃式再入模型(1)~(6)构成增广再入模型.式(15)的引入并不会改变再入问题的动力学特性,且替换了原有的过程约束. 同样将倾侧角速率作为控制量引入到增广再入模型,相应的扩张状态向量如下所示: 状态向量的初值约束和终值约束如下: (18) 增广再入模型下的轨迹规划问题P1如下所示: P1: min(13) 对动压和热流密度约束也做相同的处理,将它们转化为等式约束以及相应的状态量范围约束 (19) (20) (21) 0 (22) 此时相应的扩张状态向量如下: 状态向量的初值约束和终值约束如下: (23) P2: min(13) 跳跃式再入轨迹如图1所示.轨迹中的3个过载分界点分别用n1、n2、n3表示,称分界点的过载值为过载阈值.采用文献[17]中的定义方式,将过载分界点前后4个阶段分别定义为初次再入段、跳跃阶段、开普勒阶段和最终再入段.文献[18]指出Apollo和CEV的制导律设计中,都将n1=n2=n3=0.2g0作为过载分界点,在过载小于0.2g0的区域(初次再入段和开普勒阶段),大气稀薄、气动控制失效、倾侧角的升力控制作用对轨迹影响较小. 图1 跳跃式再入轨迹Fig.1 Skip reentry trajectory 经典跳跃式再入问题描述P0,增广再入模型下的轨迹规划问题P1和扩展增广再入模型下的轨迹规划问题P2是一个简化的再入轨迹规划描述,下面以问题P1为例按照图1所示跳跃式轨迹分段情况,给出各个阶段的具体描述. 初次再入段描述如下: (24) 式中,r0、θ0、φ0、v0、γ0、ψ0、σ0、n0表示再入点扩张状态量初值.初次再入段采取0°常值倾侧角控制.文献[18]指出在气动控制失效阶段,动压、过载和热流较小,满足约束条件,不需要考虑过程约束. 跳跃阶段描述如下: (25) 开普勒阶段描述如下: (26) 这一阶段气动控制失效,不考虑过程约束.此时一般采取常值控制策略,即u=0. 最终再入段描述如下: (27) 利用分段高斯伪谱法对上述跳跃式再入过程(24)~(27)进行规划,便获得了相应的增广再入模型轨迹规划结果. 在再入制导算法的设计中,一般考虑存在再入点状态偏差和气动参数不确定性时制导算法的鲁棒性.文献[19]中的状态初值偏差,包括高度、经度、纬度、速度,航迹倾角和航迹方位角.实际再入制导运动过程可分解为纵向运动和横向运动,在两个运动平面内走过的航程分别为纵程和横程,形成的偏差即为纵程偏差和横程偏差.本研究将纵程偏差和横程偏差作为两种状态初始偏差.下面给出两种偏差转换为对应经纬度的计算方法. 定义再入点的地心矢和期望落点的地心矢组成的平面为标准再入纵平面.飞船再入时在此平面内运动为纵向运动,偏离此平面的运动为横向运动. 地心地固系下位置坐标到高度经纬度的转换关系如下: (28) 以纵程偏差计算为例,依据给定的纵程偏差,得到纵向偏转角δR.由式(28)可计算出再入点与落点在地心地固系的方向向量a和b,进一步得到纵平面法向量vR vR=a×b 同样得到纵平面内与再入点地心矢垂直的方向向量c c=vR×a 再利用三维空间圆的参数方程解出偏差点的地心地固系坐标(xbias,ybias,zbias),利用式(28)可反解出经纬度坐标(θbias,φbias).其中三维空间圆的参数方程如下: 式中,下标x、y、z分别为向量的对应坐标分量.具体求解过程可参考文献[1]. 前面小节给出经典跳跃式再入模型下的轨迹规划问题P0和增广再入模型下的轨迹规划问题P1,以过载约束为例对这两种问题描述下轨迹规划结果进行比较分析.结果如图2所示. 图2 问题P0和P1下过载情况比较Fig.2 Comparison of the load factor between problem P0 and problem P1 其中黑色实线为问题P0下,航迹倾角取-6.1°时的过载结果;红色实线为问题P1下,航迹倾角取-6.1°时的过载规划结果;红色虚线为问题P1下,航迹倾角取-6.1°时过载的计算结果,该结果是将状态量值代入式(9)计算得到,该曲线用于验证过载规划结果的准确性.余下曲线为航迹倾角取-6.2°时的仿真结果,该对照实验用于研究微小的航迹倾角变化对不同问题过载的影响.实验结果表明,问题P0的轨迹规划结果对参数的变化比较敏感,航迹倾侧角的微小变化导致两次过载结果的剧烈差异,由上侧局部放大图可知,航迹倾角取-6.1°时,出现违反过载边界的情况,该现象的产生可能是求解器对可行域较小的非线性不等式约束处理效果较差导致的.问题P1的两次轨迹规划结果差异不大,轨迹仅在过载峰值处稍微不同,对参数变化具备较强鲁棒性.总体上看,问题P1的两次过载峰值均低于问题P0的过载峰值,较好地满足了过载约束需求.增广再入模型的建立,将不等式约束转化为等式约束及状态量的范围约束,避免了过载违反过载边界的情况发生.由下侧局部放大图可知问题P1的过载规划结果总是略微小于过载的计算结果,该偏差的产生可能是求解计算式(15)时积分误差的累积导致的,通过引入小的参数修正可减小该误差的影响.综上所述,增广再入模型的轨迹规划结果相较于经典跳跃式再入模型的规划结果,具备更好的实际应用价值. 再入点状态误差分布如表1所示.取偏差边界随机组合,得到64个初始状态点.同时对大气密度和升力系数进行拉偏处理,验证所设计的规划方法对参数不确定的鲁棒性,表2给出参数偏差条件.仿真结果如图3~5所示. 表1 初始状态误差范围Tab.1 Initial states and dispersion ranges 表2 参数偏差Tab.2 Parameter dispersion 图3为存在状态误差和参数偏差时的再入轨迹,256种参数组合下优化指标J=0,精确规划到期望落点.此时,3个过程约束结果如图4所示.全部热流小于2 MW/m2,全部动压小于20 kPa,全部过载小于6.44g0,很好地满足了设计需求,且留有较大余量. 图3 跳跃式再入轨迹Fig.3 The skip reentry trajectory 图4 过程约束结果Fig.4 The results of the path constraints 问题P1规划得到的倾侧角指令剖面如图5所示,不同参数组合给出不同的倾侧角指令,不受初始轨迹的影响.综上所述,提出的方法充分利用了返回器的控制能力,所有情况下轨迹均精确规划到期望落点,且在模型存在再入点状态偏差及气动参数不确定性时具备强鲁棒性. 图5 倾侧角指令剖面Fig.5 The command profile of the bank angle 增广动力学模型的建立用于解决图2所示过载约束违反过载边界的问题,因此仅重新定义了过载约束.而扩展增广再入模型下的轨迹规划问题P2,对其余两个过程约束也做相同的处理,将它们转化为等式约束及状态量的范围约束,问题P2的仿真结果如图6~7所示. 图6 轨迹规划结果Fig.6 The results of the trajectory planning 图6所示为单次轨迹规划结果,图7为对应的过程约束结果.其中图6(a)、6(b)、6(c)、6(d)和6(e)分别为时间-高度、经度-纬度、时间-速度、时间-航迹倾角和时间-航迹方位角曲线,图6(f)为倾侧角剖面曲线.其中蓝色实线为问题P1的规划结果,红色虚线为问题P2的规划结果.由图可知,问题P2的再入轨迹在跳跃阶段飞行时间更短,该阶段过载水平整体较低,开普勒阶段高度峰值较低,相应的总体飞行时间更短,最终再入段飞行过载峰值相应变大,满足实际飞行规律. 图7 过程约束结果Fig.7 The results of the path constraints 扩展增广再入模型的建立同样会导致过程约束规划结果略微小于过程约束计算结果的情况发生,且P2中过载、动压的偏差大小往往会大于热流的偏差大小,是过载、动压存在耦合导致的.图8给出问题P2在存在再入点状态偏差和参数不确定性时的过程约束结果.全部热流小于2 MW/m2,全部动压小于20 kPa,此时全部过载小于6.33g0,3个过程约束很好地满足了设计需求,且留有较大余量.因此,扩展增广再入模型下的轨迹规划问题P2在存在再入点状态偏差及参数不确定性情况下同样具备强鲁棒性. 图8 过程约束结果Fig.8 The results of the path constraints 针对实际再入过程对再入点状态偏差和参数不确定性具有鲁棒性需求和过载阈值前后倾侧角分段控制需求,提出一种基于分段伪谱法的鲁棒轨迹规划方法.该方法重新定义了过载约束、动压约束和热流约束,将它们转化为等式约束及状态量范围约束,建立了增广再入模型及扩展增广再入模型. 在增广再入模型与经典再入模型的比较研究中,本文提供的轨迹规划建模方法在存在再入点状态偏差和参数不确定性时具备强鲁棒性,精确规划到期望落点,且能有效地解决过载约束违反过载边界的问题.此外,扩展增广再入模型下的轨迹规划结果同样具备对初始再入偏差和对参数不确定的鲁棒性.结果表明提出的过程约束转化方法很好地解决了约束违反问题,且该转化方法不受约束类型限制,具有较强的推广性,对轨迹规划问题的求解及实际应用具有一定的指导意义.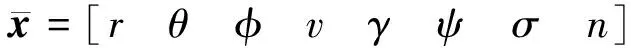
s.t.(1)-(6),(8),(10),(11),(15),(17),(18)2.3 扩展增广再入模型的建立
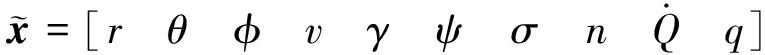
s.t.(1)-(6),(11),(15),(17),(19)-(23)2.4 经典跳跃式再入模型问题描述
3 再入轨迹分段描述
3.1 初次再入段
3.2 跳跃阶段

3.3 开普勒阶段
3.4 最终再入段
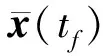
4 初始偏差计算
4.1 纵向运动和横向运动
4.2 坐标转换
5 仿真研究

5.1 参数敏感性

5.2 增广模型鲁棒性仿真研究


5.3 扩展增广再入模型研究
6 结 论

