航天器发射前动基座自对准方法比较研究
龚宇莲, 何英姿, 马 楠, 阎 师
1. 北京控制工程研究所, 北京 100094 2. 空间智能控制技术国家级重点实验室, 北京 100094 3. 中国空间技术研究院, 北京 100094
0 引 言
在航天器导航系统设计中,基于惯性测量敏感器的导航算法贯穿航天器飞行任务的各个阶段.对于入轨即要求具备一定导航精度的航天器而言,其导航任务是从飞行器发射段开始的.运载火箭发射前一般通过光瞄方式完成方位角初始对准,捷联惯组完成水平对准[1].但对于射前安装在火箭顶端整流罩内的航天器而言,如整流罩未开窗则无法获得光瞄信息,且GNSS接收机、星敏感器均无效,除可提前装订的发射场地理位置外,惯性敏感器是惟一可用测量信息源.若采用传递对准的方式,则对发射场和安装精测提出了极高的保障要求.在外界保障有限的情况下,利用捷联惯导实现全自主射前姿态自对准是这类航天器导航系统完成任务性价比最高的方案.
初始对准的结果直接影响到捷联惯导系统的导航精度.罗经对准是惯导自对准领域的经典方法,是一类从经典控制理论角度出发设计对准回路的方法[2],广泛应用于舰船[3-4]等导航平台的姿态自对准.近年也有大量研究基于罗经法的优化算法.文献[5]在分析了逆向捷联罗经对准算法的基础上,提出了一种基于逆向算法的静基座条件下快速对准方法.文献[6]用粒子群算法对罗经对准回路阻尼振荡周期参数进行寻优.此外,还有大量基于卡尔曼滤波的初始对准研究方法[7-9].
相较于罗经对准,快速、准确的初对准方法仍是研究的热门.传统的解析粗对准方法[10]无法隔离角运动干扰,只在静基座或轻微晃动条件下可用.为了解决晃动基座条件下的初对准,秦永元教授等人提出了一种应用惯性凝固假设,借助重力信息确定载体姿态的新思路[11-12],该方法忽略载体位置的变化,在摇摆基座中应用具有很大优势.惯性对准方法提出以来,被广泛应用于舰船惯性初始对准[13],车载导航初始对准[14-16]的研究中.
本文主要针对目前经典的三轴姿态自对准的方法:解析式粗对准、罗经对准、惯性系对准,通过数学仿真比对研究几种方法受敏感器测量误差的影响以及对不同工况的适应性.针对罗经法在周期性晃动基座中的应用问题,本文提出了一种将罗经回路修正周期设计为与基座震荡周期一致的简单改进方法,最后通过蒙特卡洛打靶仿真对方法进行比对分析.为一类需要从发射段即开始自主导航的航天器GNC系统方案设计提供参考.
1 解析式粗对准
解析式粗对准方法利用IMU获得地球自转角速度ωe与当地重力矢量(静止条件下加速度计测到载体受到的支持力即fb=-gb)在本体坐标系下的投影.当两个矢量不重合时,即可确定本体坐标系到当地地理坐标系的转换阵.
发射场地理纬度为BL,则地球自转矢量和支持力矢量在当地北天东系(n系)的投影为
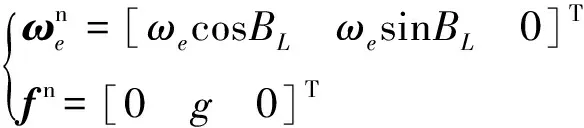
(1)
而陀螺和加速度计测量到的地球自转角速率和重力矢量在本体系(b系)下分别为

(2)
2 罗经对准法
2.1 算法描述
利用解析粗对准获得姿态初值后,即可开始导航运算,在对准阶段,北天东系下三轴失准角和水平方向的速度导航误差微分方程如下:
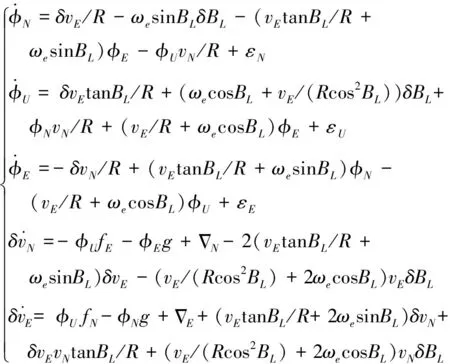
(3)
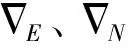
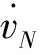

(4)
同理给出东向速度误差和失准角误差方程
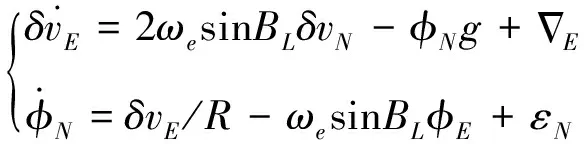
(5)
式(4)、(5)描述的误差传递特性如图1和图2的系统框图所示[4].
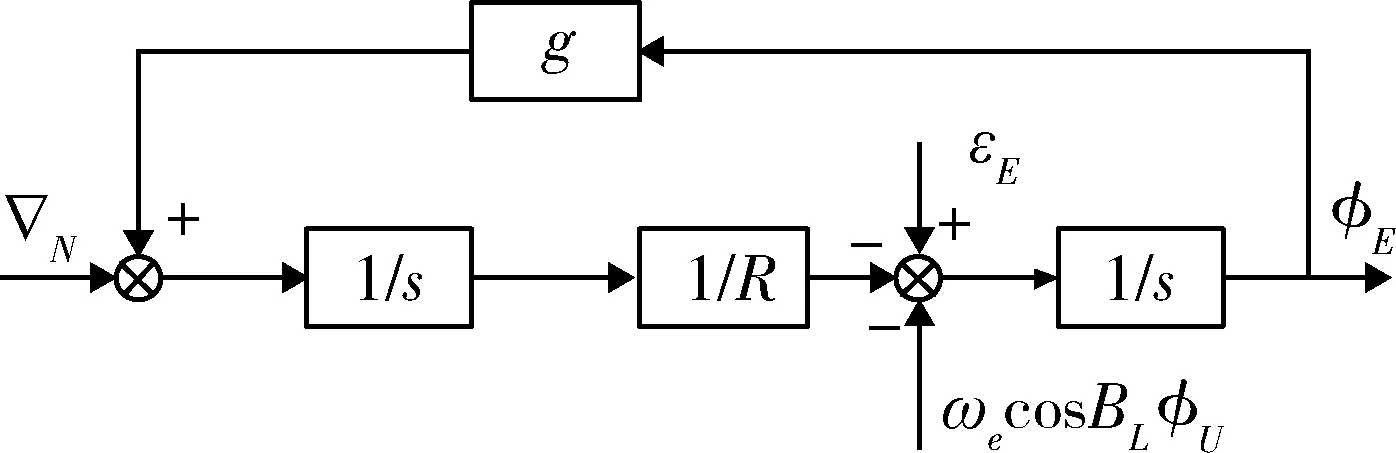
图1 北向水平误差回路Fig.1 North vertical error loop
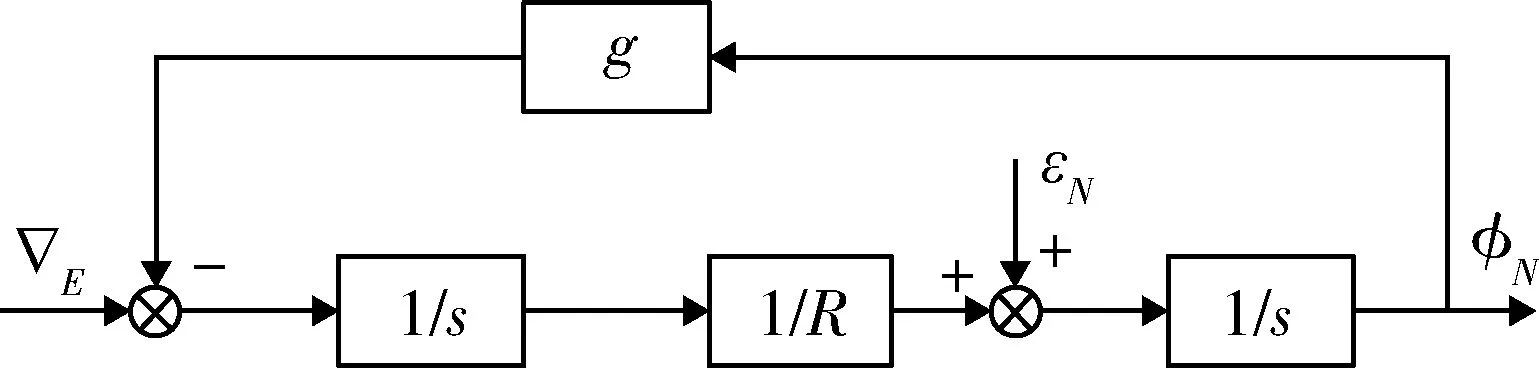
图2 东向水平误差回路Fig.2 East vertical error loop
该系统为无阻尼振荡系统,误差随时间增加而发散.从北向水平对准回路中可以看出,方位失准角φU与地球自转角速度的耦合项ωecosBLφU产生水平失准角,进而引起速度误差.罗经法对准即利用此种水平回路与方位误差的耦合关系,使用速度误差信息控制平台的天向轴,形成一个新的闭环回路,称之为罗经回路.相应的对准原理图如图3~4所示.
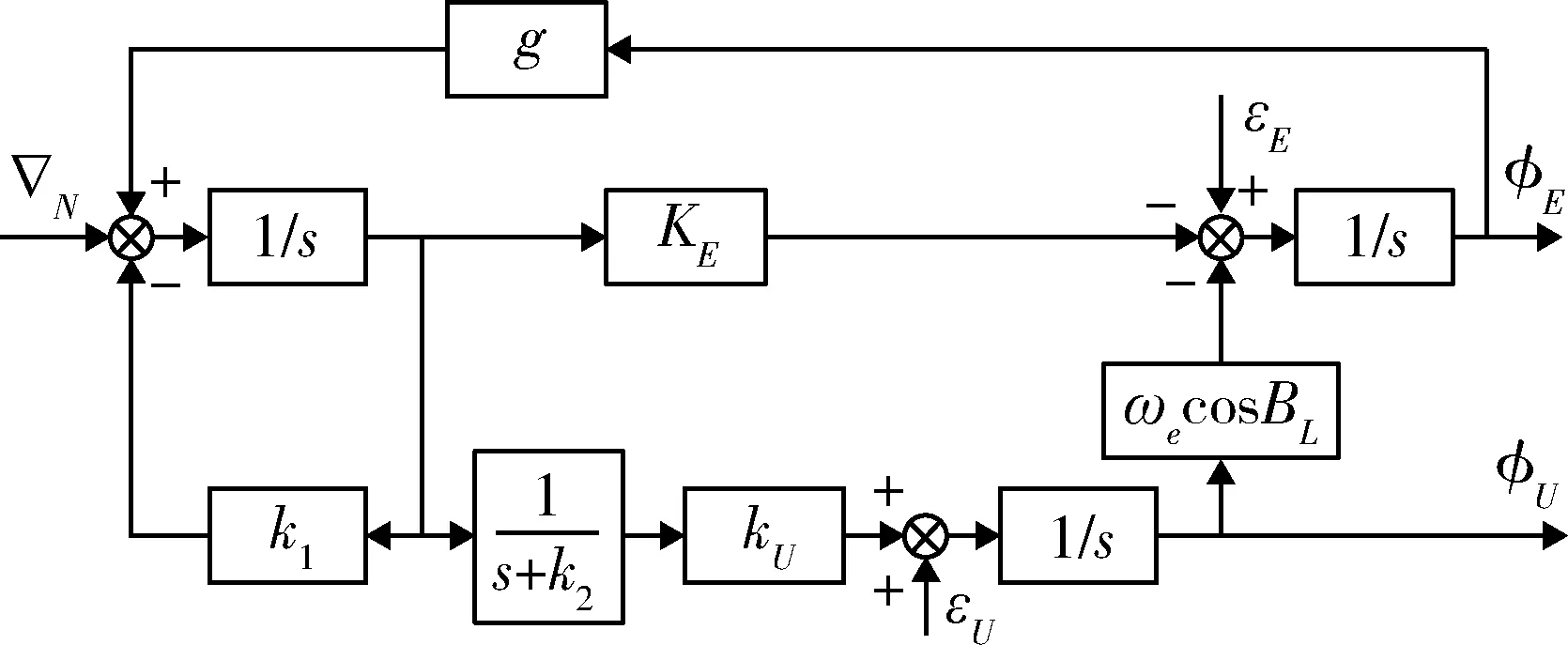
图3 罗经法对准北向回路框图Fig.3 North alignment loop of compass alignment
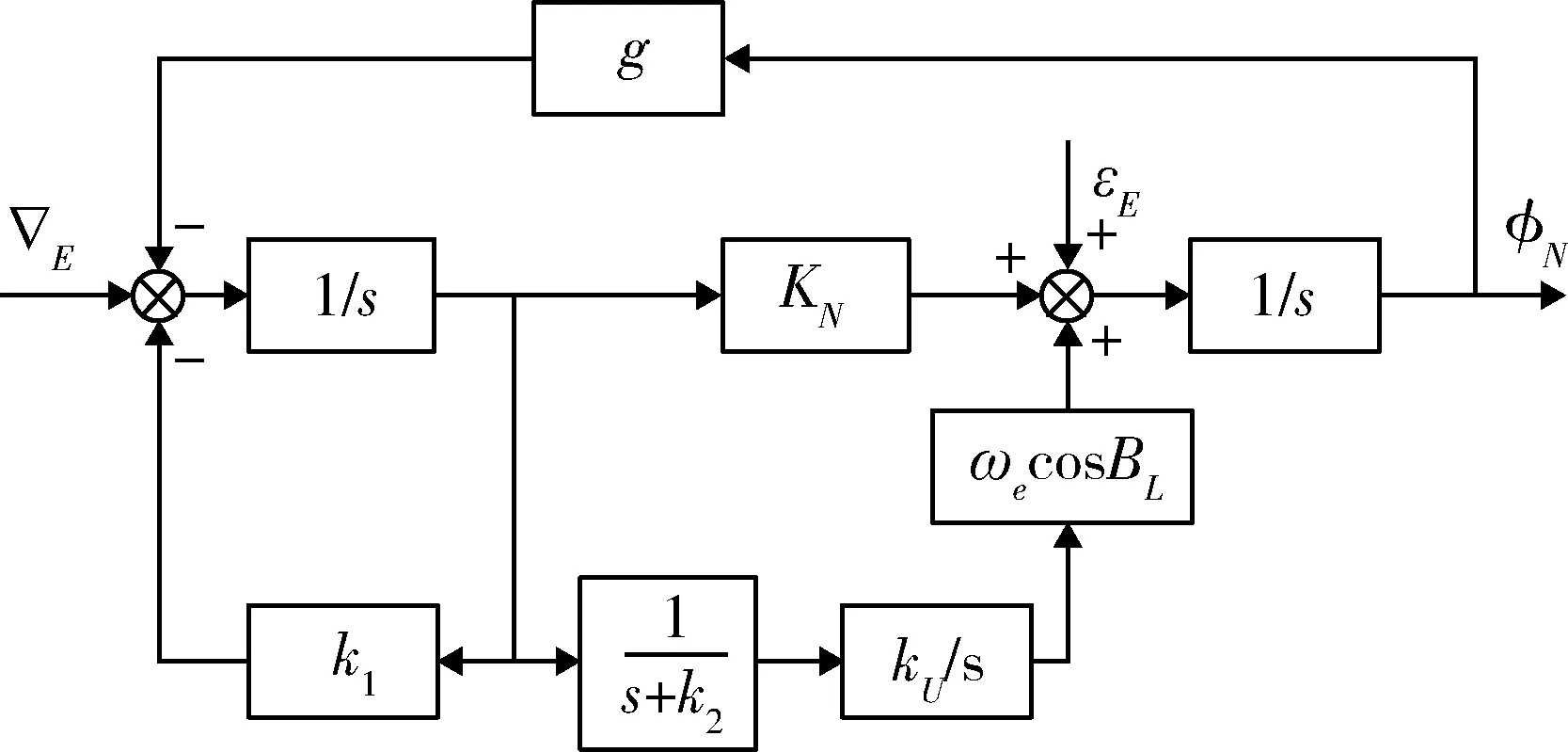
图4 罗经法对准东向回路框图Fig.4 East alignment loop of compass alignment
经罗经回路修正后,三轴失准角稳态值为
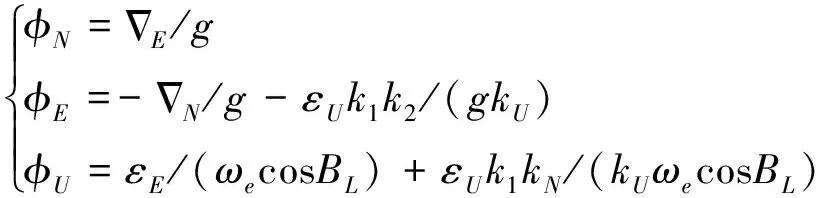
(6)
2.2 算例分析
2.2.1 静基座噪声影响分析
从图3~4的系统框图可以看出,罗经对准回路是一个高阶线性系统.该系统以加速度计测量误差作为输入,姿态角误差作为输出.加速度计测量误差包含零偏和噪声,从算法稳态误差分析结果可以看出,加速度计测量误差决定了系统的稳态误差.加速度计零偏决定了误差的极限精度,而噪声则决定了误差的波动程度.本节在静基座环境下,通过两个算例对比加速度计测量噪声对罗经对准性能的影响.
算法采用罗经对准回路,自对准算法流程如图5所示.
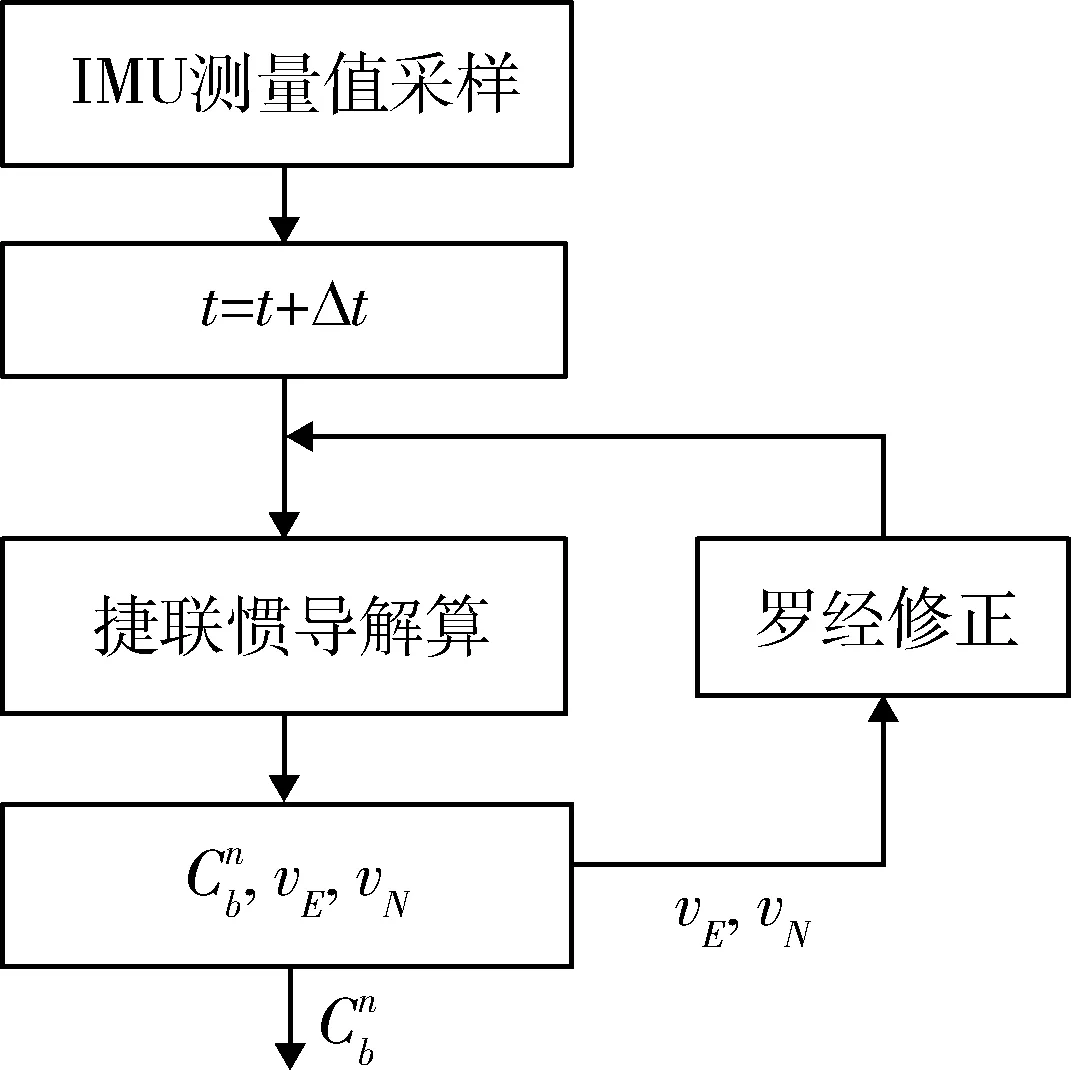
图5 罗经对准流程图Fig.5 Flowchart of compass alignment
算例1.平台为静基座,绕北天东系姿态角为AttN=AttU=AttE=0.平台所处纬度为BL=40.08°.敏感器参数设置如表1所示.

表1 敏感器参数设置Tab.1 Parameters of sensors
仿真工况:导航周期Δt=10 ms,采用图5所示流程的罗经对准回路,仿真前10s平滑数据,完成解析对准,10~500 s仅作水平对准,500 s后开始方位精对准,对准结果如图6所示.

图6 算例1三轴失准角Fig.6 Attitude error curves of case 1
算例2.平台姿态、纬度及仿真工况均与算例1一致.敏感器参数将加速度计随机噪声置为0,其余参数与算例1一致,对准结果如图7所示.
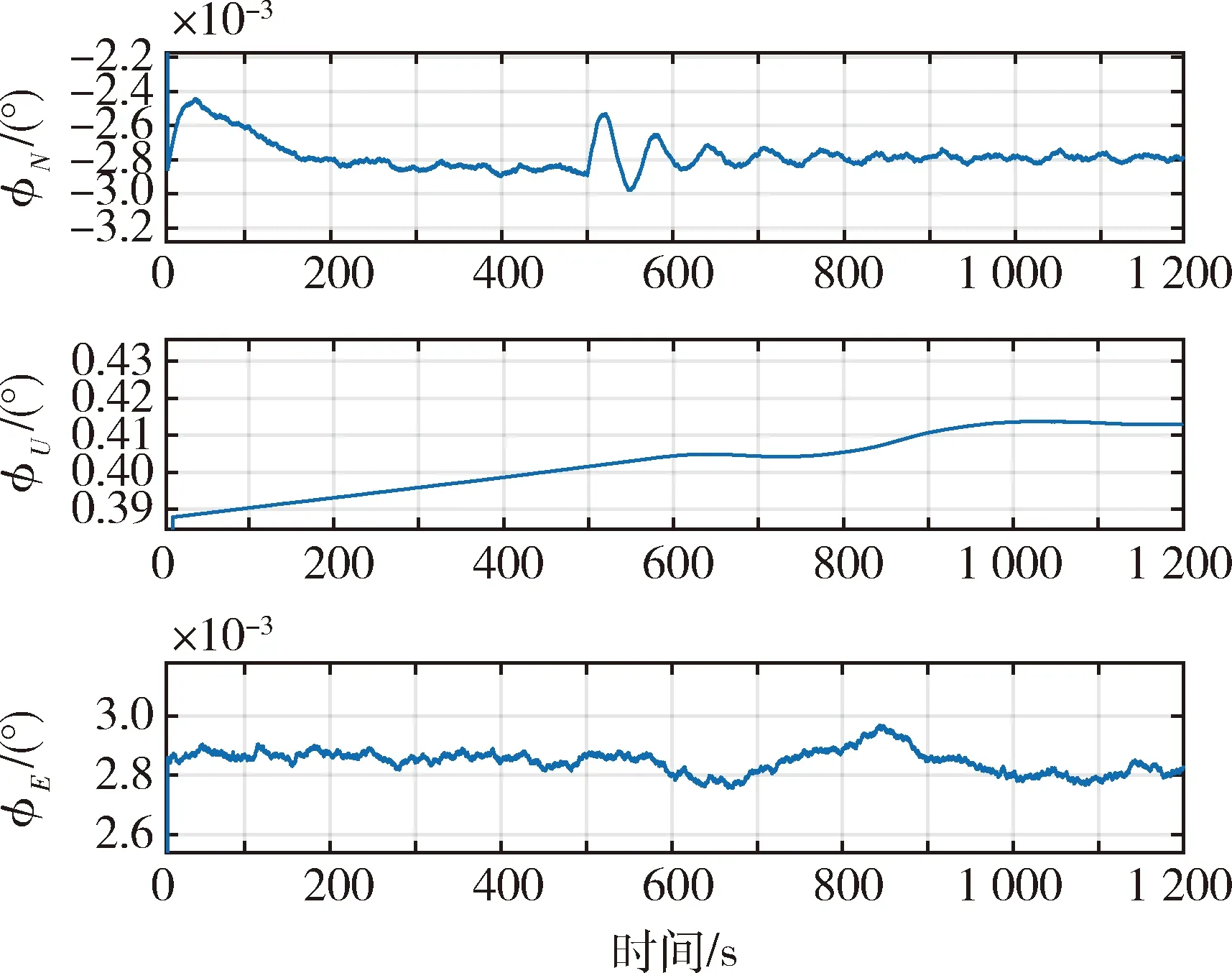
图7 算例2三轴失准角Fig.7 Attitude error curves of case 2
由表1所示的敏感器零偏,根据式(6)可知北天东三轴姿态角罗经对准的稳态误差理论值分别为:φN≈-0.002 9°,φU≈0.43°,φE≈0.002 9°.
对比算例1、算例2的仿真结果可见,在不考虑加速度计随机噪声的情况下(算例2),水平及方位失准角最终都趋于平稳且趋近于理论精度,波动范围较小.但在加速度计随机噪声存在的情况下(算例1),精对准失准角波动幅度明显增大.可见,在罗经法的应用中,加速度计随机测量噪声对自对准精度的影响比较明显.
2.2.2 晃动基座算例分析
航天器发射前置于火箭顶端,一般会处于晃动状态下.本算例考虑晃动基座下罗经法的适应性问题.算例3~5仿真工况设置中初始阶段均采用解析粗对准得到姿态初值,由于解析粗对准只能统计一段时间的均值,不同的统计时长将得到不同的初值.因此本节3种工况设置中采用不同的解析对准时长,分析初值对晃动基座罗经对准的影响.
算例3.平台姿态采用三轴晃动基座,数学模型如下所示:
Atti=Atti0+Atti1sin(2πfi1t+φi1)+
Atti2sin(2πfi2t+φi2)+Atti3sin(2πfi3t+φi3)
上式中,i=N,U,E,三轴晃动参数分别如下:
fE1=0.1,fE2=0.2,fE3=0.4;
AttE1=2.0°,AttE2=0.2°,AttE3=0.02°;
fN1=0.1,fN2=0.2,fN3=0.4;
AttN1=2.0°,AttN2=0.2°,AttN3=0.02°;
fU1=0.05,fU2=0.1,fU3=0.2;
AttU1=1.0°,AttU2=0.1°,AttU3=0.01°.
相位φi1,φi2,φi3随机,平台纬度、敏感器参数均与算例1一致.
仿真工况:导航周期Δt=10 ms,采用采用图5所示流程的罗经对准回路,仿真前10s平滑数据,完成解析对准.10~300 s执行水平精对准,500 s后开始方位精对准,对准结果如图8(a)和图9(a)所示.
算例4.平台姿态、纬度及敏感器设置均与算例3一致.仿真前50 s平滑数据,完成解析对准,其余与算例3一致,结果如图8(b),图9(b).
算例5.平台姿态、纬度及敏感器设置均与算例3一致.仿真前100 s平滑数据,完成解析对准,其余与算例3一致.仿真结果如图8(c)和图9(c).

图8 晃动基座下改进的罗经对准流程Fig.8 Flowchart of improved compass alignment on moving base
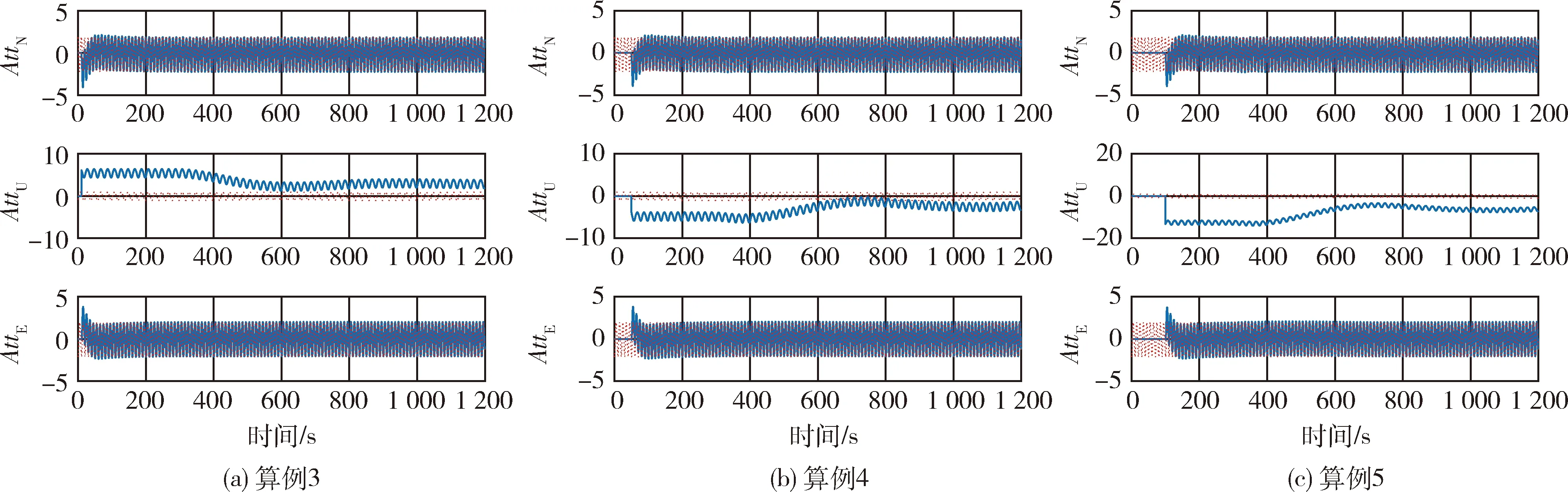
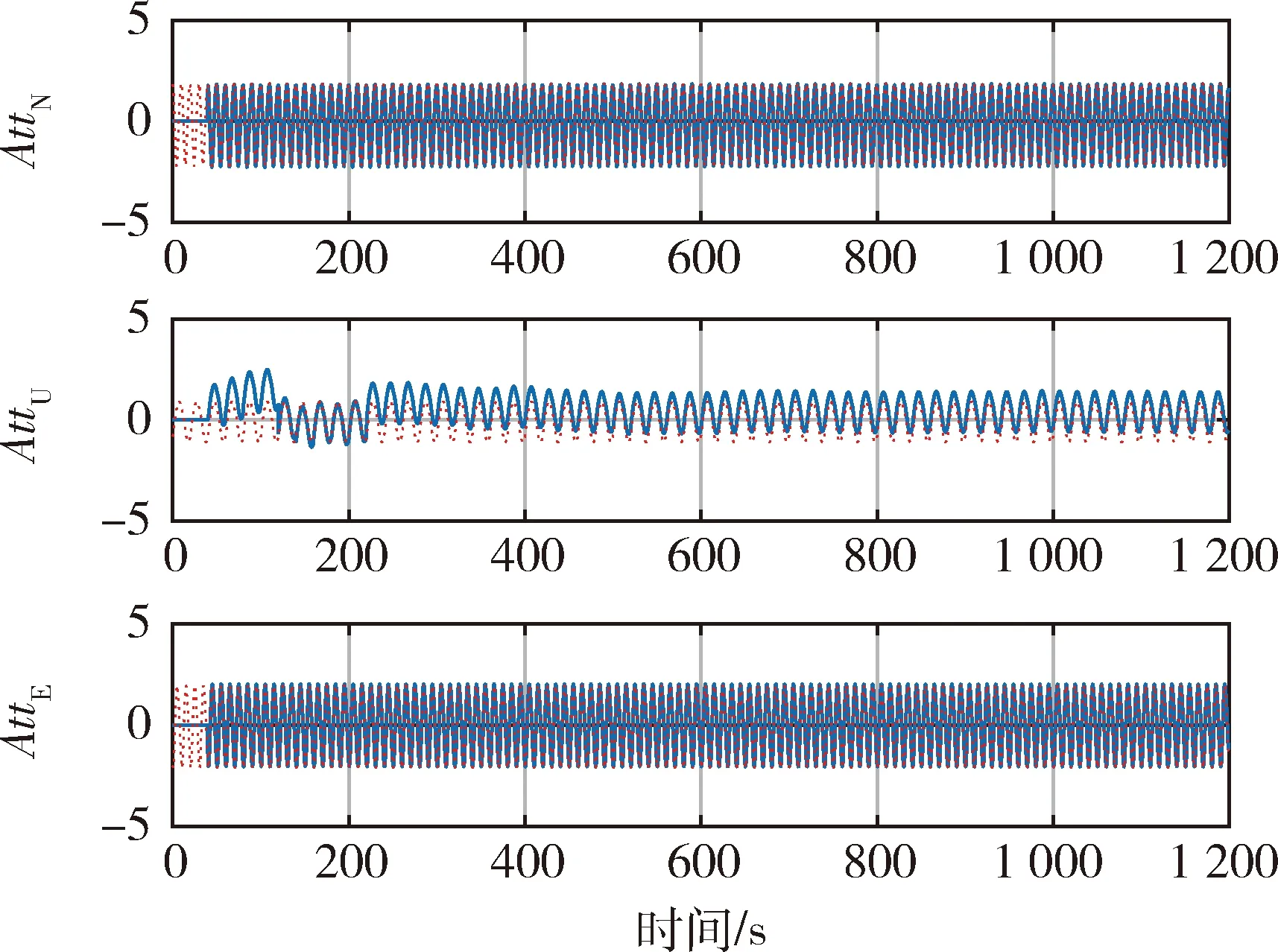
图9 算例3~5三轴姿态角(虚线)及对准结果(实线)Fig.9 Attitude of three axes(dashed line) and alignment angles(solid line) curves of case 3-5
从算例3~5对比结果可见,北向和东向失准角尽管存在波动,但均收敛至0.1°左右.而方位失准角则偏离真值较远,且3个算例方位失准角最终分别收敛至3°,-2°,-5°左右.可见直接采用罗经对准,在晃动基座情况下最终对准结果无法收敛到真值附近,对准结果不可信.
2.3 晃动基座下罗经法应用改进
从罗经对准原理可以看出,罗经法假定水平速度增量为零,将惯导递推的水平速度增量作为误差引入回路修正角度.而航天器待发段导航平台随箭体晃动,线速度同样周期性波动,与罗经法假设条件存在差异.发射段箭体处于相对静止的状态,箭体以一定的基频晃动.在实际工程中,箭体晃动的基频一般可以提前获得.假定已知箭体晃动周期为T,则箭体顶端航天器的速度如式(7)所示周期性变化
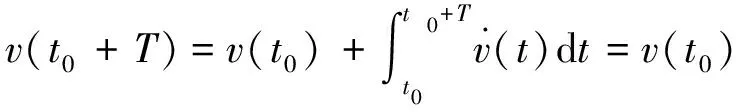
(7)
式(8)说明一个周期惯导积分的速度增量为零
因此本文利用整周期速度增量为零的特性改进罗经法,将图5的罗经修正回路修正周期改为如图8所示.捷联惯导仍按Δt导航周期解算,罗经修正回路则以T为周期进行修正.
算例6、7、8采用图10所示改进的罗经修正流程,其他仿真工况与设置与算例3、4、5一一对应,仿真结果如图11和图12所示.
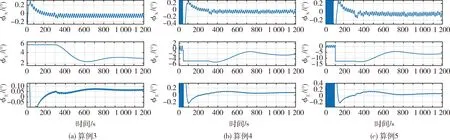
图10 三轴失准角Fig.10 Attitude error curves of case 3-5
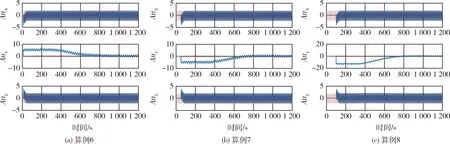
图11 算例6~8三轴姿态角(虚线)及对准结果(实线)Fig.11 Attitude of three axes(dashed line) and alignment angles(solid line) curves of case 6-8
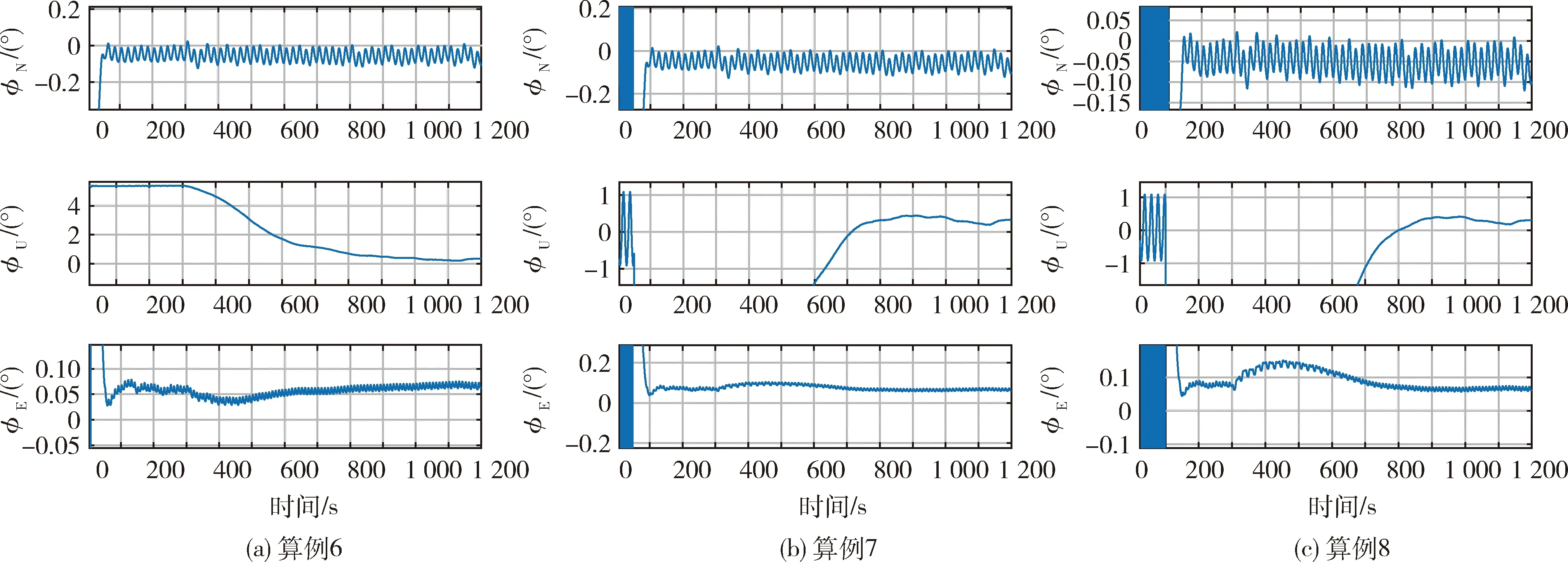
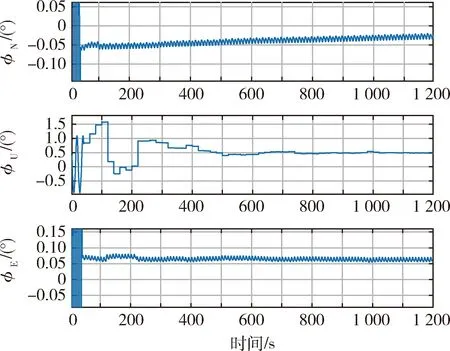
图12 三轴失准角Fig.12 Attitude error curves of case 6-8
从算例6~8可以看出,采用罗经修正周期与基频一致的改进算法后,3种工况下最终失准角收敛结果一致,尽管存在一定幅度的波动,但均收敛至理论误差值附近.因此,在基频可知的情况下,通过设置与基频一致的罗经回路修正周期,可以适用于周期性晃动基座的自对准.
3 惯性系对准算法
3.1 算法描述
惯性系对准是针对晃动基座初始对准提出简单易用的对准方式,其基本原理是地球转速度是一个已知量,在确定时间内当地重力加速度在惯性空间内转过的角度可精确得到,由于重力矢量包含地球的北向信息,进而可以间接分析载体系与导航系之间的姿态阵[12].算法将姿态阵分解为4个相关矩阵的乘积形式
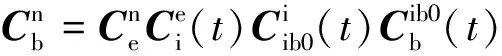
(8)
式(8)中
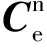
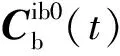
在动基座情况下,加速度计测量值在载体惯性系下的分量如下:
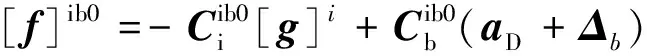
(9)
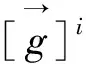
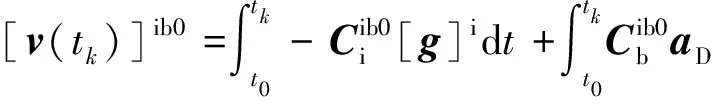
(10)
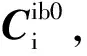
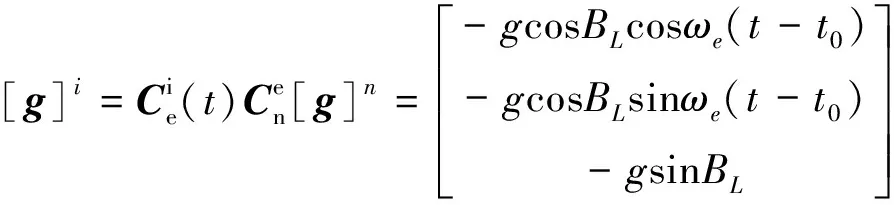
(11)
上式积分得到
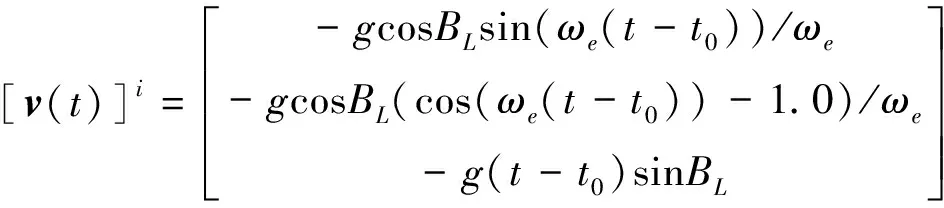
(12)
选择tk1,tk2两个时刻(t0 惯性对准本质上仍是一种双矢量定姿算法,但与解析式粗对准直接利用重力矢量和地球自转矢量不同,惯性对准利用了重力矢量一段时间在惯性空间的积分量.积分过程显著地降低了随机噪声的影响. 算例9.算例9采用的平台姿态、纬度、敏感器参数均与算例3一致.自对准算法采用惯性系对准,仿真结果如图13和图14所示. 图13 算例9三轴姿态角(虚线)及对准结果(实线)Fig.13 Attitude of three axes (dashed line) and alignment angles (solid line) curves of case9 图14 算例9三轴失准角Fig.14 Attitude error curves of case 6-8 从仿真结果可见,在周期性晃动工况下,北天东系三轴对准结果均快速收敛,且收敛结果波动小.但随着时间的推移,北向姿态对准结果逐渐增大,增大趋势与北向陀螺等效零偏积累特性一致. 本文给出了一种适用于周期性晃动基座自对准的改进罗经修正算法,根据前文分析,该算法与惯性对准算法均可适用于周期性晃动工况下的姿态对准.本节通过蒙特卡洛仿真,比对两种算法在航天器待发段随箭体晃动情况下的自对准性能.仿真工况采用算例3所描述的姿态晃动模型,分别采用本文给出的改进罗经修正法和惯性对准方法并行计算.敏感器参数设置如表2所示.仿真结果如图15和图16所示. 图15 罗经法对准三轴姿态误差Fig.15 Attitude error curves of compass alignment 图16 惯性系对准三轴姿态误差Fig.16 Attitude error curves of inertial frame base alignment 表2 敏感器参数设置Tab.2 Parameters of sensors 本文针对航天器待发段位于火箭整流罩内随箭体周期性晃动的典型工况,比对研究了解析式粗对准,罗经对准和惯性系对准3种算法的适用性. 由于解析式粗对准一般需对一段时间内采样到的惯性敏感器数据进行平滑后求解,因此在晃动基座的工况下难以直接应用.但解析粗对准可以为罗经对准提供初值,在实际应用中仍然不可忽视. 在针对罗经对准的算例分析中可以看出,由于罗经对准利用了水平速度增量为零的假设,因此当载体周期晃动,线速度不为零时不能直接应用.本文针对周期晃动特性,在已知晃动基频的情况下,利用周期性晃动整周期速度增量为零的特性,将罗经对准回路修正周期设置为基频周期的整数倍.仿真显示这种应用改进可以适用于航天器发射段姿态自对准.但罗经法在工程应用中需要设计复杂的高阶罗经回路参数,受到加速度计随机噪声影响后对准结果波动幅度较大,且对准收敛时间也比较长的特性,使其在实际应用中需要结合敏感器特性以及任务对精度的需求综合考虑. 惯性系对准方法本身即是针对摇摆基座的姿态自对准进行设计,且算法简单、设计难度小,对敏感器的随机噪声不敏感,因此对航天器发射段姿态自对准是适用的.但根据本文的分析可知,对准时间过长或过短均不利于提高惯性系对准精度.因此在工程应用中,惯性对准方法的应用需要重点考虑对准时长.3.2 算例分析
4 蒙特卡洛仿真比对
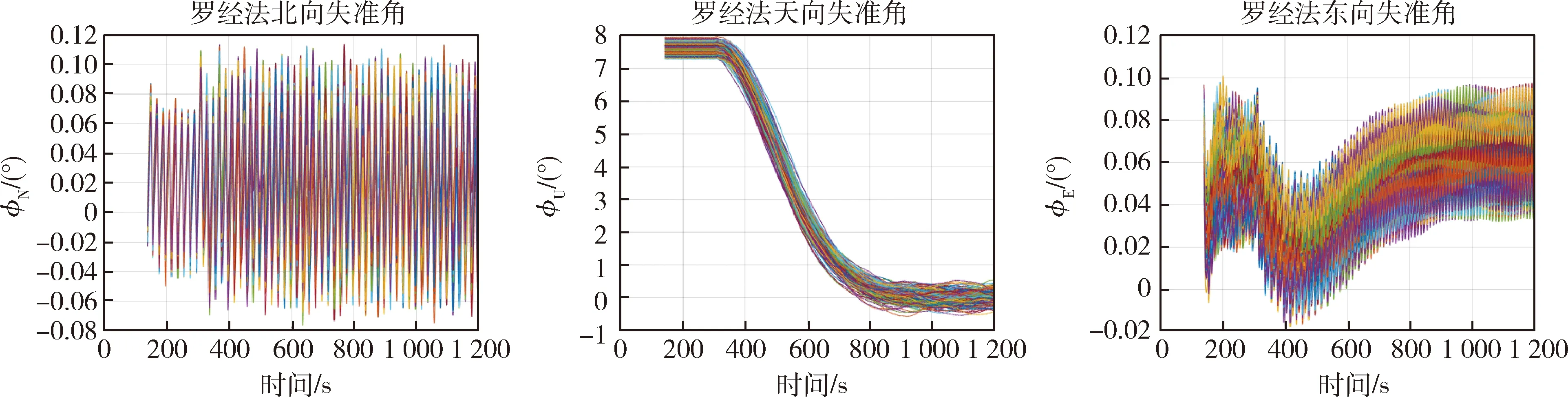
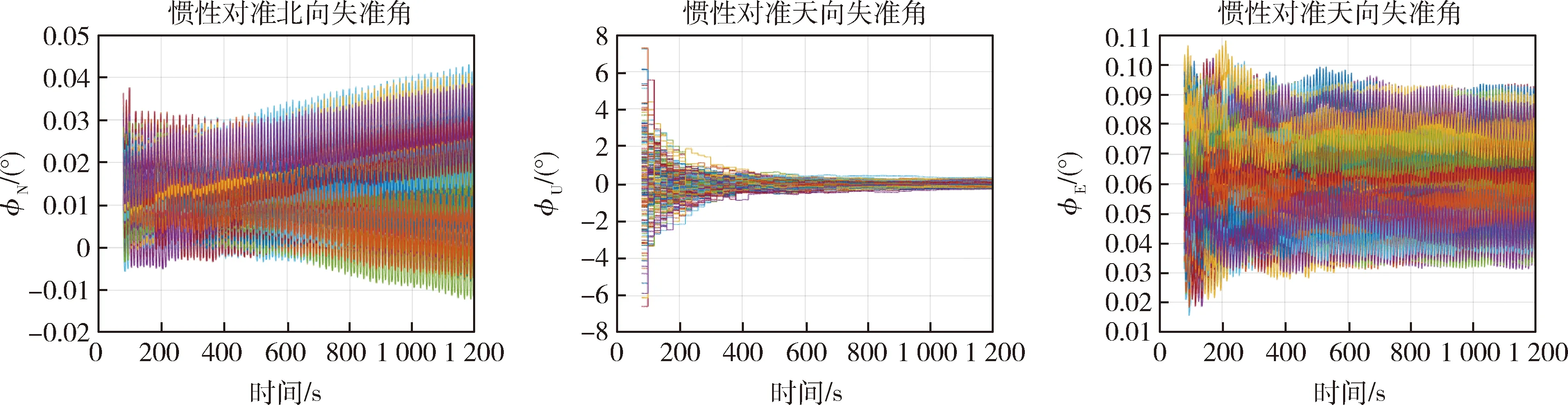

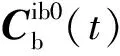
5 结 论

