一种基于故障及欠驱动情况的反作用轮配置优化方法

冯佳佳, 谢 军, 黎 飞

1. 北京控制工程研究所，北京100094 2. 空间智能控制技术重点实验室，北京 100094

0 引 言

自主控制是航天器控制系统设计追求的一个重要目标.在有限的配置资源下，如何最大程度增加航天器自主控制的能力，这是摆在我们面前首先需要解决的问题[1-2].

对于航天器控制系统中的执行机构来说，其在整个寿命阶段一般经历正常工作、一重故障、二重故障等几个阶段，其在控制方式表现为全驱动控制和欠驱动控制两种方式.而在故障及欠驱动情况下执行机构的控制能力问题是航天器自主控制的一个重要体现，一方面它可以有效增强航天器自主运行能力，在故障模式下仍然能够正常的运行；另一方面它也可以有效减少控制系统的设计成本，在航天器设计的时候选择欠驱动控制模式[3].因此，从这个角度出发，对航天器控制系统中的执行机构从故障及欠驱动情况进行配置优化研究具有重要的工程意义[4-5].目前，从故障及欠驱动情况对执行机构进行配置优化的研究相对欠缺，其主要集中在故障及欠驱动情况下的控制算法上[6-10].事实上，对执行机构从故障及欠驱动情况进行配置优化，一方面需要保证所配置的执行机构在整个寿命阶段都能够保证航天器控制能力的最优，另一方面也要保证所配置优化的执行机构简洁、可靠，这样的配置优化目标也是符合目前航天器工程发展的需求.

由于反作用轮是航天器控制系统中较常用的一种执行机构[11]，因此，本文将主要针对经典、简洁的4轮装反作用轮进行配置优化研究.首先，根据反作用轮配置的目的进行4轮装反作用轮配置优化问题的描述；其次，根据其在整个寿命阶段可能发生故障的情况，对它在故障阶段的控制性能进行具体分析；然后，根据4轮装反作用轮在每个阶段的控制能力建立反作用轮配置优化模型，从而寻找出在全寿命阶段下的最优配置；最后，以一工程实例进行配置解析，并针对可能发生的3种工作阶段进行仿真验证，以验证其自主运行能力.

1 问题描述

设某航天器配置4个同一类型反作用轮作为执行机构，其由航天器星体和反作用轮组成的动力学方程为

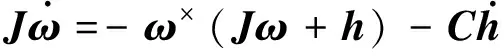
(1)

其中，J=diag{I1,I2,I3}为航天器系统(包括反作用轮)的转动惯量矩阵，ω=[ω1ω2ω3]T为航天器相对惯性系的角速度在本体系下的分量，ω×为反对称矩阵，h为反作用轮相对星体的角动量，C为反作用轮的配置安装矩阵，其可以描述为

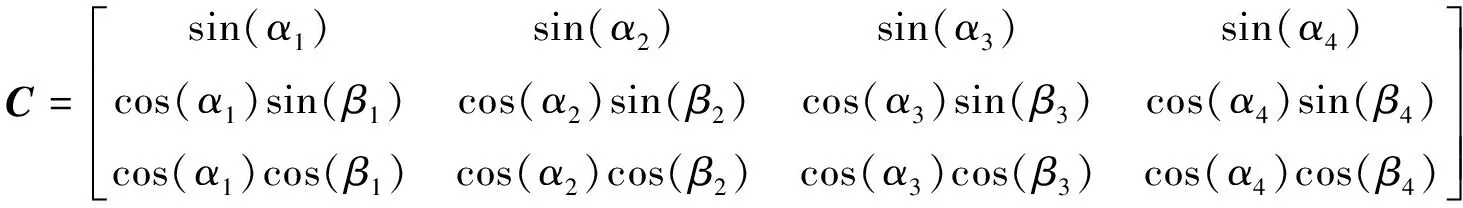
(2)

式中，αi,βi,i=1,2,3,4为反作用轮的安装夹角，αi∈(αi,min,αi,max),βi∈(βi,min,βi,max).由于反作用轮在进行配置安装时，一般出于某种原因或者考虑，对反作用轮的安装夹角有一定的约束范围，其可描述为

f(αi,βi)<0

(3)

如何确定αi,βi,i=1,2,3,4的具体安装夹角，使反作用轮在整个寿命阶段均能保证航天器控制能力最优，包括全驱动控制阶段和欠驱动控制阶段，这是本文研究的重点.

2 反作用轮全寿命阶段控制能力分析

一般为了保证控制系统中所配置的4轮装反作用轮可用性最高，一般要求任意3个反作用轮均不共面.同时，在这里假设所配置的单个反作用轮的可靠性为p0.

(1) 正常阶段

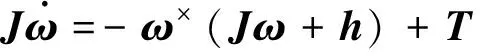
(4)

从式(4)可以看出，T作为动力学方程中的唯一输入，其控制能力的大小主要体现在其具体数值上.因此，很显然，为了提高控制系统的控制性能，一般需要最大化安装矩阵C所围成的角动量包络体积V1.角动量包络V1越大，则代表着作用于航天器的反作用轮输出范围越大，控制能力越强.

其中，在冗余控制模式中，对于确定的输入T一般采取伪逆分配法[12]，将所需要的角动量分配到每个具体的反作用轮上.

(2) 一重故障阶段

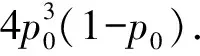
(3) 二重故障阶段

根据KRISHNAN等[13]研究指出，如果控制系统的角动量为零，则仅配有不平行的两个反作用轮的航天器系统是可控的，其中，航天器控制系统的角动量可以通过磁力矩器或者推力器等非零角动量装置进行卸载，并最终满足系统角动量为零这一条件.

当系统角动量为零，则式(4)变为

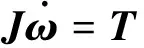
(5)

假设发生二重故障后剩余工作的两个反作用轮的安装方向单位矢量为n1,n2，则式(5)变为

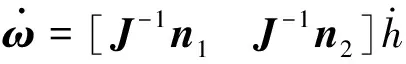
(6)

令

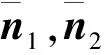
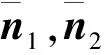
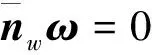
(7)

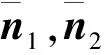
(4) 三重故障阶段

这里三重故障阶段主要指的是控制系统有3个反作用轮发生故障，其中，在该阶段的概率为4p0(1-p0)3，由于在该阶段的概率基本为零，所以该阶段反作用轮的控制能力不做讨论.

3 反作用轮配置优化

由于反作用轮配置矩阵所围成的角动量包络面和角动量包络体是反作用轮配置优化的重要指标，因此需要首先建立角动量包络面和角动量包络体的计算方法.

(1) 角动量包络面和角动量包络体计算方法

设有m个反作用轮，其配置安装矩阵为

A=[A1A2…Am]

(8)

其中，Ai为第i个反作用轮安装方向的单位矢量，i=1,2,…m.

各个反作用轮输出的正、负方向的角动量记为hi,max和hi,min，且有

hi,min≤hi≤hi,maxi=1,2,…,m

(9)

其中，hi.max为第i个反作用轮的正向最大控制输出，hi,min为第i个反作用轮的负向最大控制输出.

在这里假设各反作用轮角动量组成的列向量为hw=[h1h2…hw]T，则反作用轮组合控制输出为

h=[h1h2…hm]T=

[A1h1A2h2…Amhm]T=Ahw

(10)

当A中任意3×3列向量线性无关时，其角动量可达集边界由一系列平行四边形组成的封闭包络面，并且原点将包络于可达集内部[14].可达集的体积可以拆分为原点和各四边形组成的四棱锥体积之和[15]

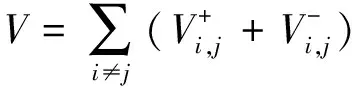
(11)

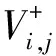
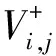
(12)

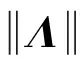
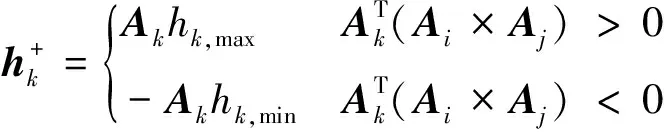
(13)

四棱锥底面面积为

Si,j=(hi,max-hi,min)(hj,max-hj,min)sin(〈hi,hj〉)=

liljsin(〈hi,hj〉)=liljsin(〈Ai,Aj〉)

(14)

其中，li=hi,max-hi,min,lj=hj,max-hj,min，〈hi,hj〉表示hi,hj间的夹角，也即Ai,Aj间的夹角，且有

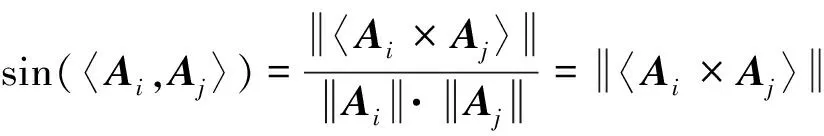
(15)

其中，式(14)也可作为角动量包络面的计算公式.

故式(12)化简为

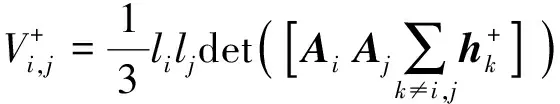
(16)

同理有

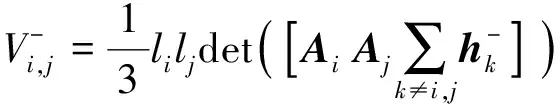
(17)

其中

(18)

(2) 反作用轮配置优化模型的建立

由上面的分析可以看出，反作用轮在每一个工作阶段的控制能力.因此，综合以上的分析，为了寻求反作用轮的配置在整个寿命阶段均为最优，反作用轮的配置优化模型可以建立为

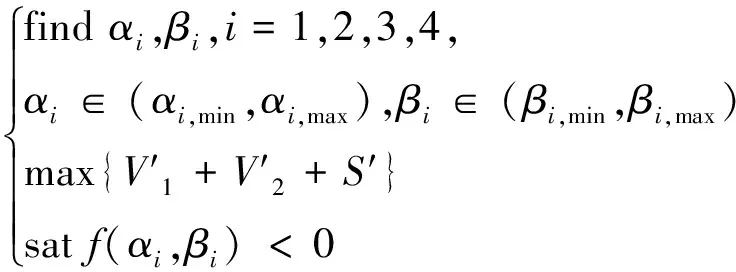
(19)

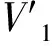
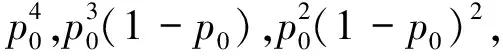
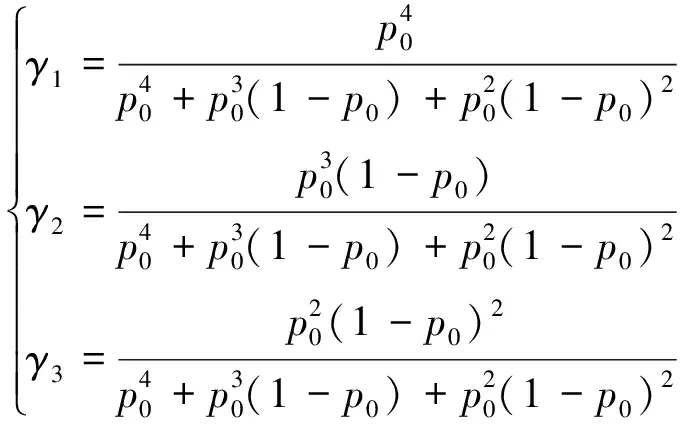
(20)

引入客观设计概率权重后，式(19)修正为

(21)

式(21)即为反作用轮在考虑整个寿命工作阶段所建立的配置优化模型，其主要考虑了正常阶段、一重故障阶段和二重故障阶段3个阶段.

4 优化算法

粒子群优化算法(PSO)是一种典型群智算法,其最大的优点是实现简单，全局搜索能力强，应用广泛,可以广泛的应用于非线性、不可微、多极值、高维函数的优化问题[16].

因此，针对PSO优化算法的优点，在对所建立的反作用轮配置优化模型上，选择PSO算法进行优化.

PSO算法表达式为

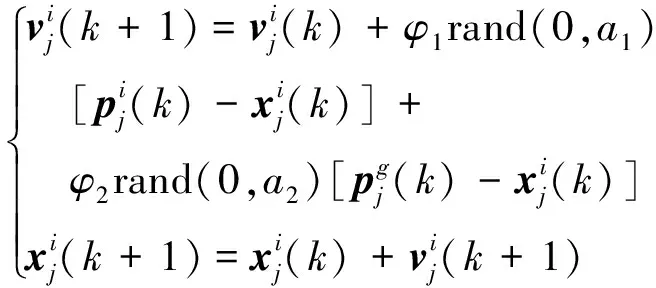
(22)

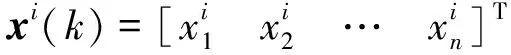
5 实例解析

为了验证本文所提出的反作用轮配置优化方法的有效性，现进行工程实例解析：

设某一控制系统需要进行反作用轮配置，航天器转动惯量为：J=diag{3 200,2 400,1 500}(kg·m2)，符号diag{·}表示对角阵.所配置4个反作用轮的力矩和角动量分别为0.1 N·m、50 N·m·s.设航天器控制系统设计时对反作用轮安装角的限制约束范围为

设单个反作用轮的可靠性为p0=0.99(16年寿命要求)，则归一化后的客观概率设计权重为

γ1=0.989 9,γ2=0.01,γ3=0.000 1

利用PSO算法对式(21)进行优化，得到的配置优化矩阵为

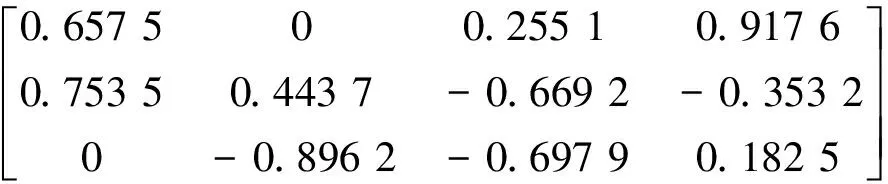
此时对应的反作用轮安装角度(单位rad)为

β1=1.570 8,β2=2.681 9,β3=3.905 9,β4=5.189 2,α1=0.717 5,α2=0,α3=0.258 0,α4=1.161 9.

为了验证所优化配置矩阵的控制效果，下面将针对反作用轮工作的3种情况进行仿真.

仿真情况1.主要针对正常情况.仿真时间为2 000 s，仿真步长为0.1 s,分配矩阵采取伪逆分配方法，其仿真具体控制任务为：航天器的3个轴从[0 0 0]T进行[π/3 π/4 π/6]T的角度机动，航天器姿态机动没有进行路径规划.

由于PID控制算法目前广泛应用于实际航天器的控制中，为了真实验证本文配置优化的效果，控制算法在这里选取为PID.其中，控PID制参数选取为

Kp=diag{5,2,1}，

Kd=diag{8 000,3 000,3 000}

仿真结果如图1所示.

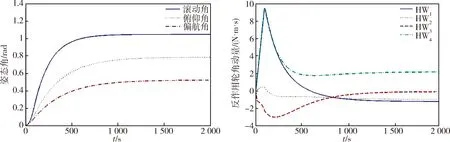
图1 正常情况Fig.1 Normal working condition

从图1可以看出，在正常情况下，即反作用轮无故障发生时，配置优化的矩阵可以很好的完成姿态机动任务，而且控制性能较好.

仿真情况2.主要针对反作用轮发生一重故障的情况，其具体仿真参数如情况1，仿真结果如图2～5所示.

从图2～5可以看出，当发生一重故障时，即有一个反作用轮发生故障时，在相同的控制参数下，优化配置矩阵仍然可以有效的完成控制任务，从而证明配置优化方法有效.

图2 反作用轮1发生故障Fig.2 Failure of Reaction Wheel 1

仿真情况3.主要针对发生二重故障的情况，此时进入欠驱动控制模式，此时假设控制系统角动量为零.由于在欠驱动控制模式下，普通的控制方法将无效，在这里选取基于势函数的欠驱动控制方法[17]，其中其关键参数取值为λ=1 000，g=50，λ代表调节姿态误差和角速度误差间的比率，g为姿态角速度的比率.其具体控制任务和情况1一致，仿真结果如图6～11所示.

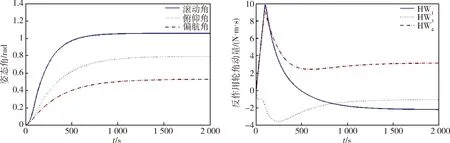
图3 反作用轮2发生故障Fig.3 Failure of Reaction Wheel 2

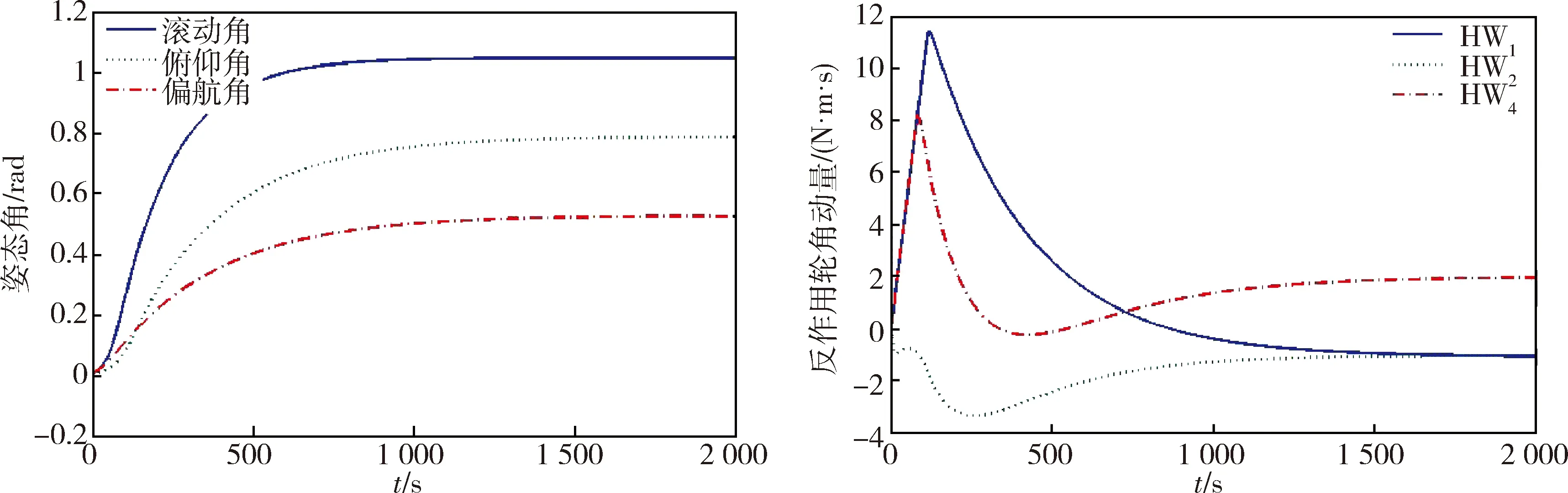
图4 反作用轮3发生故障Fig.4 Failure of Reaction Wheel 3

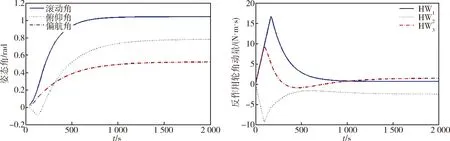
图5 反作用轮4发生故障Fig.5 Failure of Reaction Wheel 4

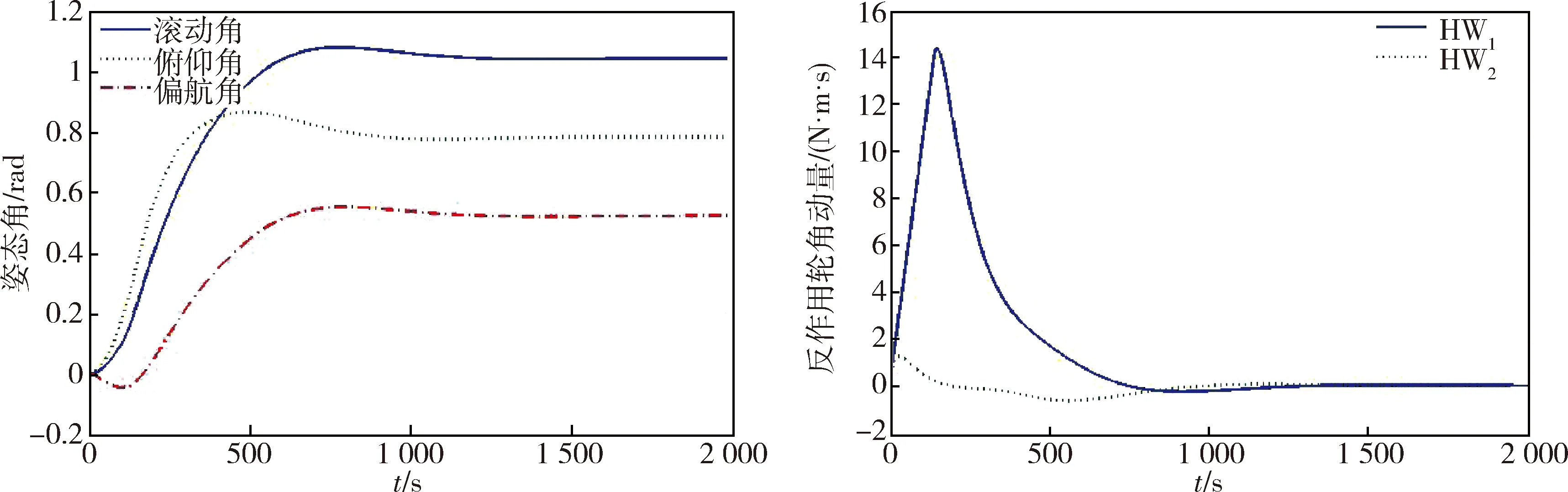
图6 反作用轮3、4发生故障Fig.6 Failures of Reaction Wheel 3 and 4

图7 反作用轮2、4发生故障Fig.7 Failures of Reaction Wheel 2 and 4

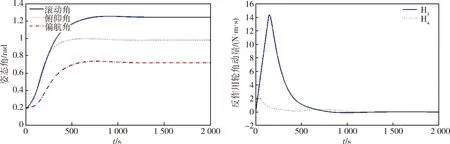
图8 反作用轮2、3发生故障Fig.8 Failures of Reaction Wheel 2 and 3

图9 反作用轮1、4发生故障Fig.9 Failures of Reaction Wheel 1 and 4

图10 反作用轮1、3发生故障Fig.10 Failures of Reaction Wheel 1 and 3

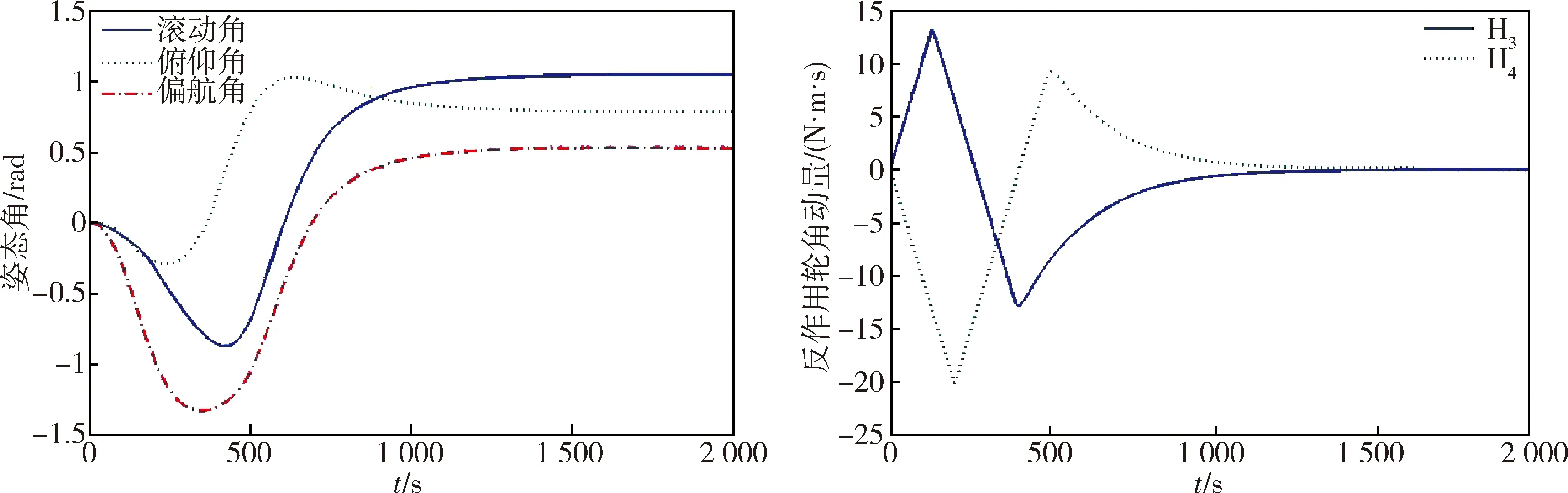
图11 反作用轮1、2发生故障Fig.11 Failures of Reaction Wheel 1 and 2

从图6～11可以看出，在二重故障下，即有两个反作用轮同时发生故障时，所配置优化的矩阵仍然能够有效的完成航天器机动控制任务，从而证明配置优化的矩阵可行.

从整个仿真结果上可以看出，本文所提出的反作用配置优化方法针对正常情况、一重故障情况和二重故障3种情况均能够有效的完成航天器姿态机动控制任务，从而证明本文所提出的配置优化方法的可行性和有效性，可以有效的提升航天器自主运行的控制能力.

6 结 论

对航天器控制系统中的执行机构从全寿命阶段，即考虑全驱动控制模式和欠驱动控制模式下进行配置优化研究具有重要的工程应用意义.本文突破了目前只从控制算法上去提升航天器自主运行控制能力的局限，提出了一种考虑故障及欠驱动情况下的反作用轮配置优化方法，从执行机构的本质控制属性去考虑，并利用该方法对一工程实例进行配置解析，并针对可能发生的三种工作阶段进行仿真验证，结果表明本文所提出的配置优化方法能够有效提升航天器的自主运行，从而证明本文所提出的方法可行和有效，具有一定的工程应用价值.

然而，在进行反作用轮配置优化上，本文主要从执行机构的控制能力，即反作用轮的输出能力上去研究，然而还有很多方面没有进行考虑，如驱动控制和耦合控制的关系、具体的控制性能和控制任务、具体的欠驱动控制算法等，这都将作为下一步研究的重点及方向.