基于视觉导航的自主小行星弱引力场测量方法
付亮勇, 胡锦昌,2*, 刘一武, 邓家权
1. 北京控制工程研究所,北京 100094 2. 空间智能控制技术国家级重点实验室,北京 100094 3. 63798部队,西昌 615606
0 引 言
近年来,小行星探测已成为主要航天国家深空探索领域的重点发展目标之一[1].由于小行星具有密度分布不均匀、形状不规则和运动状态复杂等特点,导致小行星的引力场极为不规则和复杂;此外,探测器在小行星附近受到太阳中心引力、快速自旋的非球形摄动力以及太阳光压摄动力等作用,使其在近小行星处轨道动力学复杂多变[2-3].不规则小行星引力场确定问题是小行星探测任务中下降着陆和采样返回阶段顺利实施的关键难点之一.
小行星的引力场需要采用合适的引力模型来描述,常用的引力建模方法主要可分为级数逼近法和三维模型逼近法[4].级数逼近法主要通过无穷级数来逼近引力势能,可以得到解析形式,主要有球谐函数模型法[5]和椭球谐函数模型法[6];球谐系数可通过地面测定轨数据和星上自主导航算法解算得到,对于还未进行探测的小行星来说无法事先获取其准确的引力信息[7].三维模型逼近法主要采用简化的三维模型来逼近小行星不规则形状,然后通过数值计算方法得到引力势能,进而完成引力建模,主要有三轴椭球体模型法[8]和多面体模型法[9];三维模型逼近法可利用天文观测或掠飞拍摄图像信息以完成模型建立,可以在任务发射前获取目标天体的近似引力模型.
由小行星引力场发展来看,目前对小行星引力场研究以测定轨数据反演为主,而利用三维模型正演为辅;如何将两者数据结合起来,建立精确且便于轨道分析的不规则引力场模型是将来研究重点.文献[10]提出一种联合导航数据和小行星形状模型建立精确引力场模型的方法,有效解决了密度分布不均匀难题;文献[11-12]提出利用小行星形状模型和经初步定轨数据反演解算的引力场模型对小行星进行密度分布估计,然后从估计的密度分布中重新构建表面引力场,其精度显著提高.
目前,公开文献中,对于较大的目标小行星,引力场测量大多是采用稳定绕飞轨道,通过地面测定轨和星上相对测量数据相结合的方式进行反演.对于弱引力的小行星,则一般适合采用近似直线上下自由运动的方式,如隼鸟2号的探测目标“龙宫”.对于上下运动的测量方式,其难点在于自由运动弧段一般较短,难以通过积累长时间测量数据以提高反演精度,而对于直径为百米量级的小行星[13]来说,其特殊性困难在于:引力更弱,其准确测量难度更大;自由运动弧段一般只有数个小时,数据积累长度更短;地面定轨精度不足以支撑引力场测量,需依赖星上相对测量实现;在引力场测量过程中,一般需要同时辨识小行星的自旋角速度大小和方向等参数.针对上述问题,提出一种通过视觉导航方式获取相应的量测信息,进而依靠星上自主完成引力场测量的方法;还仿真分析了小行星整体质量分布差异下的不同飞行轨迹的反演结果,进而提出根据整体质量分布来规划引力测量中探测器的飞行轨迹.
1 系统轨道动力学模型
通过定轨数据进行小行星引力场反演,首先需要建立高精度的轨道动力学模型,以模拟探测器的轨道真值和推导反演过程所需的系统状态矩阵.小行星附近轨道动力学复杂,受多种摄动力作用,包括太阳中心引力、小行星中心引力及其快速自旋的不规则形状摄动力、大行星引力摄动和太阳光压摄动等作用[14].在模拟探测器的轨道真值时,系统轨道动力学模型应建立在J2000日心黄道惯性坐标系下.
1.1 探测器轨道动力学模型
探测器轨道动力学系统如图1所示.以太阳为中心引力体的探测器轨道动力学方程为
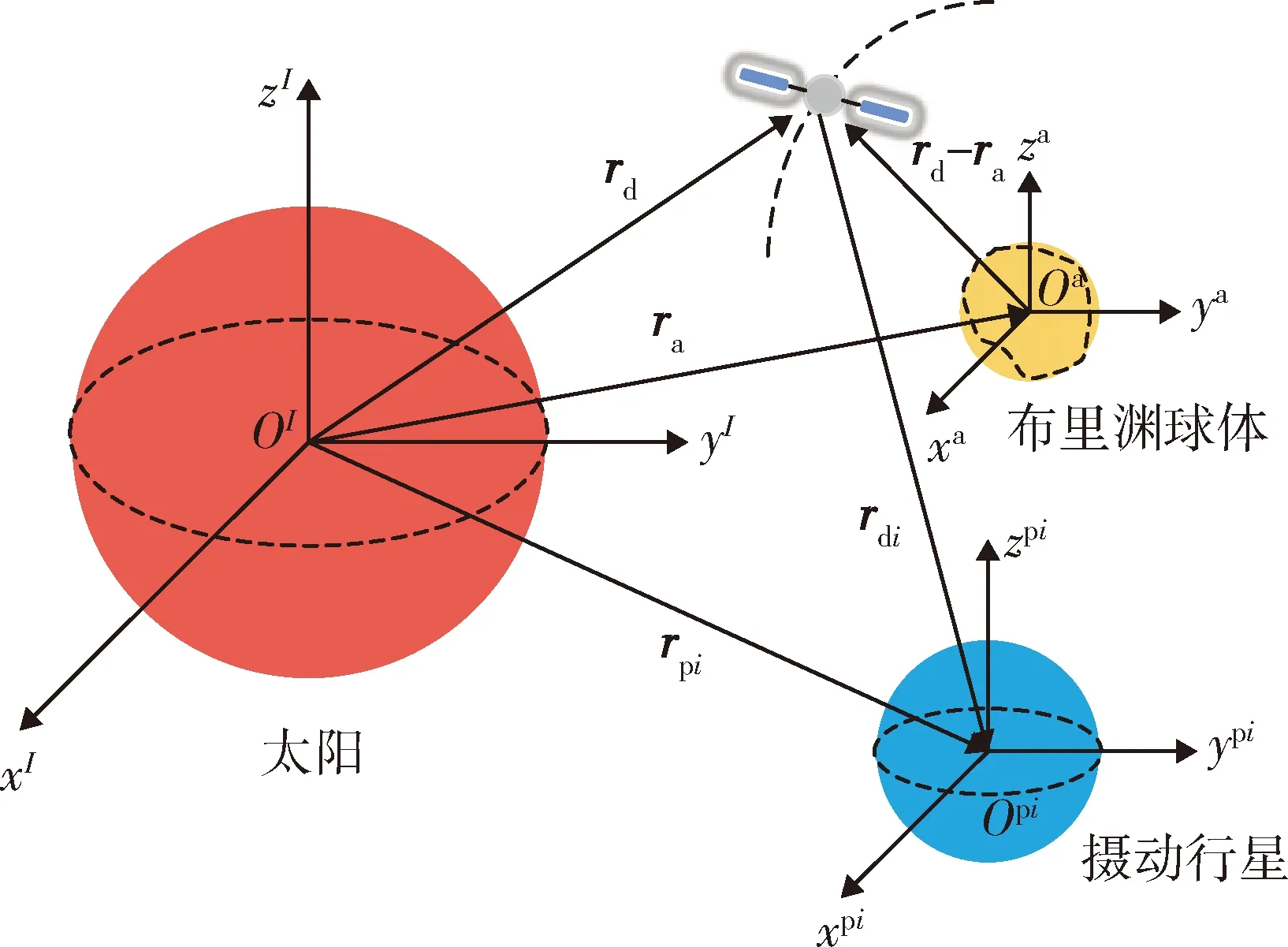
图1 探测器轨道动力学系统Fig.1 Probe orbit dynamics system
(1)
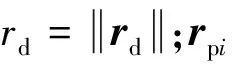
(2)
式中:μ是小行星引力常数;ra是小行星相对太阳的位置矢量;aE是小行星不规则引力场去除中心引力部分的非球形摄动加速度,需要注意的是,非球形摄动加速度是在小行星固联坐标系下定义的.
1.2 小行星轨道动力学模型
假设太阳光压力对小行星的轨道影响可以忽略,以太阳为中心引力体的小行星轨道动力学方程为
(3)

1.3 小行星球谐函数模型
对于小行星不规则引力场,通常可以使用下面的引力能势函数表示
(4)
式中:RE为小行星参考半径,参考量的作用只是用来无量纲化球谐系数,并不影响球谐函数模型的收敛条件;Cnm、Snm为球谐系数,且有C00=1,Sn0=0;n为阶数,m为次数;Vnm、Wnm具体表达式如下:
(5)
式中:r为检验点到中心天体质心的距离;Pnm(sinφ)是sinφ的缔合勒让德多项式[15];φ、λ分别是地心纬度和地理经度,即探测器受到的不规则引力摄动是在中心天体固联坐标系下描述的.
为方便计算探测器所受不规则引力摄动加速度的解析式,下面给出式(5)的递推公式[16].
初始条件
递推公式
(6)
式中,x、y、z分别为检验点在小行星固联坐标系下各坐标轴的分量,将式(6)代入式(4)便可得到递推形式的小行星不规则引力场的球谐模型.
式(4)中球谐系数是一组用来描述小行星质量和形状分布的参数,C00=1表示一均质球体的引力势,而后面各级数项表示对均质球体引力势的修正.
为了方便本文对各球谐系数和引力常数的估计,需要对式(4)进行变形,下列还是采用原来符号,不加以区分,但需要注意其中区别;引力势能模型重写为
(7)
式中,C00≠1,并且引力常数μ=C00·RE,式(7)中的球谐系数跟式(4)中的相差固定的倍数,下文出现的球谐系数均是按式(7)约定的,这样将所有待估计的球谐系数确定好后,引力常数也就确定好了,上式中球谐系数即反映了引力场的全信息.
需要注意的是,当描述引力场模型的固联坐标系原点和小行星质心重合时,建立在固联系下的球谐系数一阶项C10、C11、S11均为0;并且若固联坐标系的z轴与小行星惯量主轴方向一致时,球谐系数项C21、S21均为0[17].
2 系统测量模型
为简化分析反演算法,文章是在小行星形心固联坐标系和实际的小行星固联坐标系重合下研究的,下文统称为小行星固联坐标系.
在实际任务中,应在进行引力场测量前,完成对目标小行星三维建模以获取特征点的三维位置,进而构建导航特征库[18-19].利用视觉导航获取的图像信息来完成对小行星引力场测量,其观测量的定义为:导航特征点在小行星固联坐标系下的三维位置;导航特征点在相机成像相平面上的像素坐标,即像元p和像线l坐标值,其表达式为
(8)

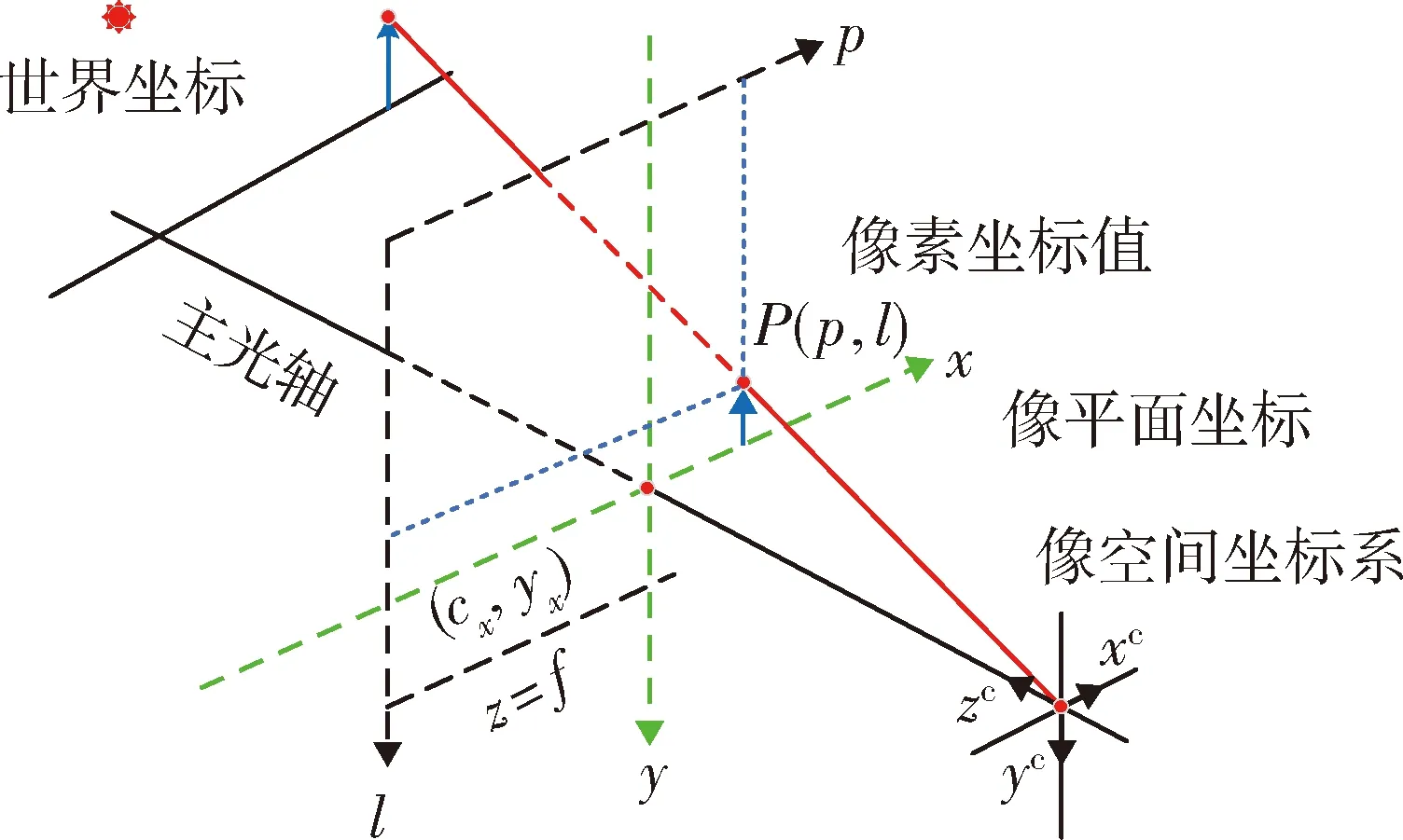
图2 导航相机成像模型Fig.2 Navigation camera imaging model

(9)
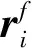
设惯性系到小行星固联系的坐标系按照313顺序进行转动,则式(9)中方向余弦矩阵CFI的具体表达式为
CFI=C3,ωaCFI0=C3,ωaC3,γC1,βC3,α
(10)
其中:ωa为小行星自旋角速度大小;下标i=1,3表示旋转轴,α、β、γ分别表示绕各轴的转角,其中α、β代表了自旋轴的方向;CFI0表示初始时刻小行星固联系相对于惯性系的方向余弦矩阵.
系统测量方程
(11)

(12)
其中,δij为狄拉克函数.
假设待估计的初始状态为x0,则测量敏感矩阵为
(13)
3 引力场参数反演方法
3.1 系统状态转移矩阵
为推导反演算法所需要的系统状态转移矩阵,首先需要求取探测器在小行星惯性系下的轨道动力学方程;用式(1)减去(3)可得
(14)
考虑到在实际引力测量阶段,探测器离小行星最远距离不超过几百米,而小行星相距太阳在1 AU左右,可算出式(14)中括号项部分所引起的加速度摄动量级远小于受小行星不规则引力摄动量级,故可经简化消去[20];并且将小行星不规则摄动加速度aAST用式(6)~(7)替换,经整理,最终可得到探测器在小行星惯性系下的轨道动力学方程为
(15)
式中,v为探测器在小行星惯性系下的速度矢量,a为其他未建模误差项,rF为探测器在小行星固联系下的位置矢量,U为包括各阶摄动项的引力势能函数.
系统的状态方程通常由探测器的相对轨道动力学方程、姿态运动学方程和姿态动力学方程组成.而在引力场测量阶段,姿态可以认为是直接测量得到的已知量,因此状态方程可以不考虑姿态运动学和动力学;并且假设太阳光压是完全已知的,其模型误差可忽略,由于观测时间只有数小时,忽略其它未建模摄动力的影响.此外,因小行星自旋角速度大小和方向难以事先获得准确值,需要作为未知状态量一同估计.
由此,系统的状态变量X定义为
X=[rT,vT,Cnm,…,Snm,α,β,λ,ωa]T
(16)
因此系统的状态方程f(X)表达式为
(17)
将探测器初始时刻的状态预测值(先验值)当作初值,通过积分得到预估的探测器轨道,由此得到特征点的像元像线预估值,然后和光学相机实际测量的特征点像元像线值比较,并根据最小二乘批处理算法得到初始状态的修正值;此过程需要经过多次迭代,不断修正初始先验模型参数和其它待估状态初值,以此得到最终符合收敛要求的引力模型.为了实现对初始状态的更新,需要求取状态转移矩阵,为此需要先对状态方程线性化,即求取系统状态方程f(X)对系统状态的偏导数矩阵,如下所示:
(18)
由此可得到离散化后的状态转移矩阵
(19)
3.2 系统观测矩阵
对式(13)的敏感矩阵进行求解,令系统待估计的初始状态x0为
(20)
将式(9)代入式(13),并根据式(19)可得到系统量测模型的第i的特征点的观测矩阵为

(21)
其中,Φ(t,t0)|3×[(n+1)2+6]为取状态转移矩阵的前3行,xa,0=[α,β,λ,ωa],n是待求取的引力模型阶数.
3.3 加权最小二乘批处理法
考虑到观测方程的强非线性和过多估计参数,并且待估参数量级较小,若在最小二乘迭代过程中,状态增量过大会容易导致不收敛;对此可以利用待估参数的先验信息来将其尽量保持在收敛范围内.因此可将最小二乘残差意义下的代价函数扩展为[10]
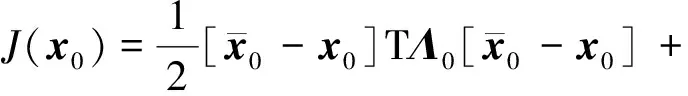
(22)

利用最小二乘批处理算法估计初始状态量x0的原则是:通过合理的选择近似修正项δx0,使线性化的预测残差的加权平方和J(x0)最小.
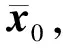
(23)
式中:Jk、Jk+1分别为上一次和下一次的代价函数迭代值;η为事先指定的小量;对于迭代终止条件还可以采用,当δx0小于某个值等.
3.4 探测器飞行轨迹规划
理论上通过无穷阶球谐函数模型可以逼近任意形状的小行星在其布里渊球体外的引力势,但是由于无穷阶本身是无法计算的,通常取其重要项,因此存在截断误差,在本文主要分析其四阶以内的性质.取余弦面球谐函数Pnm(sinφ)cos(mλ),绘制其表示的引力势分布情况如图3所示,对于正弦面球谐函数Pnm(sinφ)sin(mλ)而言,它与余弦面球谐函数只是在经度上相位相差90°,前者绕极轴旋转90(°)/m即可得后者,情况本质上一致.

图3 四阶余弦面球谐函数引力势分布示意图Fig.3 Gravity potential distribution of four-degree cosine surface spherical harmonic function
图3中展现了四阶余弦面球谐函数的引力势情况.第一个是均质球体的引力势分布,余下的第一列是带谐项,对角线上是扇谐项,其余的是田谐项;暗的地方引力势为负,表示此处质量相比于均质球体来说不足;亮的地方引力势为正,表示此处质量相对均质球体来说是聚集的.
由上分析可知,球谐系数反映了小行星的整体质量分布情况,因此可以根据其整体的质量分布来规划探测器相对于小行星的飞行轨迹,以此来反演出球谐模型.对于质量主要沿纬度方向变化的采用南北竖直轨迹;对于质量主要沿经度方向呈扇形分布的采用东西横向轨迹;但对于质量主要沿经纬度方向呈凹凸田块状分布的无法直接给出探测器的飞行轨迹,从直观上看,存在竖直、横向以及倾斜飞行轨迹,实际中可能需要用不同方向的轨迹或者相同方向但相对于小行星不同位置的轨迹下量测值组合反演,需要进一步研究.
虽然不规则小行星的密度不均匀,无法获取其准确的质量分布,但是密度在一定范围内变化,其形状大致可以决定其整体质量的分布,因此可根据三维建模获取的图像信息大致了解其整体质量分布,进而规划探测器飞行轨迹以此进行引力场测量,该方法并不依赖于目标天体精确的质量分布信息.
设直径为百米量级的某小行星引力常数为0.115 m3/s2,参考半径为100 m,均质半径为50 m;其四阶以内球谐系数参考433Eros并加以调整,上述3种典型质量分布差异情况下的球谐系数设置如表1所示;其对应的探测器飞行轨迹如图4~图6所示.

图4 质量呈带状分布Fig.4 Mass distribution in bands

表1 整体质量分布差异下球谐系数Tab.1 Spherical harmonic coefficients under different mass distributions
后续将针对这几种情况进行具体的仿真校验,验证在引力场测量中以小行星整体质量分布为依据来规划探测器飞行轨迹的合理性.
4 仿 真
本节首先通过仿真分析典型质量差异下的引力场测量情况,来对上述提出的探测器轨道规划方案进行校验;然后在此基础上对直径为百米量级的目标小行星进行引力场测量,由于其实际球谐系数未知,本文参考433Eros的球谐系数来设定.除上文中已经合理假设参数外,设目标小行星自旋周期为30 min,实际误差为5%;方向角α、β、γ分别为30°、60°、10°,实际误差各5°.
考虑相机视角条件,探测器的速度脉冲和初始位置在小行星瞬时轨道坐标系下给定;此外仿真中导航特征库是根据模拟球体和三维建模误差构建出来的;导航敏感器参数如表2所示.

表2 导航敏感器参数Tab.2 Parameters of navigation sensor
4.1 质量分布差异下飞行轨迹分析
3种质量分布下的球谐系数标称值已在表1给出;其先验值和标准差如表3所示.在距离小行星表面30 m位置左右施加速度脉冲,使探测器远离小行星,在小行星引力场作用下自由运动,各质量分布下的探测器轨迹采用图4、图5和图6中设计的轨迹;仿真时间为2 500 s,特征点提取间隔为30 s左右.

图5 质量呈扇形分布Fig.5 Mass distribution in sectorial shape
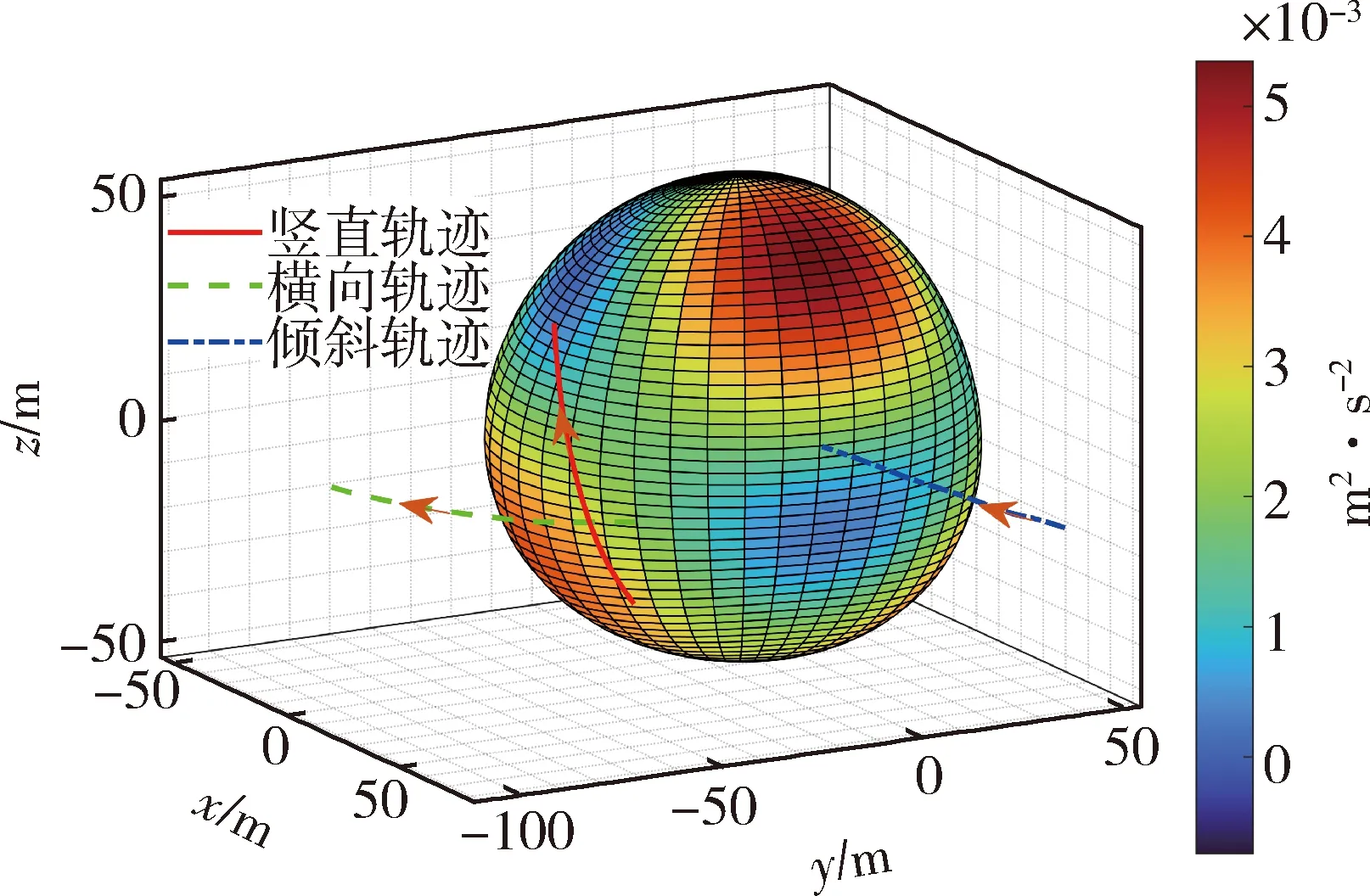
图6 质量呈田块分布Fig.6 Mass distribution in non-strict symmetry

表3 球谐系数先验值和标称值Tab.3 Prior and nominal values
由图7可知,对于整体质量沿纬度方向呈带状分布的小行星,在引力场测量时,采取南北竖直向轨迹,其最大误差不超过10%,而对于横向轨迹,最大误差超过了20%,由此可见探测器的相对飞行轨迹采取南北竖直向较好.

图7 质量呈带状分布下引力测量误差Fig.7 Measurement errors under banded distribution
由图8可知,对于整体质量沿经度方向呈扇形分布的小行星,在引力场测量时,采取东西横向轨迹,其最大误差不超过10%,而对于竖直向轨迹,最大误差可达到20%,由此可见探测器的相对飞行轨迹采取东西横向较好.

图8 质量呈扇形分布下引力测量误差Fig.8 Measurement errors under sectorial distribution
由图9可知,无论哪种飞行轨迹,其大部分区域测量误差都在10%以上;由此可见对于整体质量沿经纬度方向呈凹凸田块状分布的小行星,由于其质量在经度和纬度方向均存在聚集和缺失,导致单一方向下一条探测器飞行轨迹的测量数据无法准确解算其全局引力信息,应当组合多条不同轨迹下的定轨数据进行反演.图10是在上述横向轨迹反演的基础上,将其当作先验值,再次利用一条中纬度附近起始的倾斜轨迹下量测数据进行迭代优化结果.
由图10可知,经不同轨迹下量测数据组合反演后,其引力场测量精度明显提高,绝大部分区域测量误差不超过10%;图9和图10仿真结果对比表明,对于质量并不只沿某一方向分布的小行星来说,需要组合不同相对位置下的定轨数据以充分反演其引力信息.

图9 质量呈田块分布下引力测量误差Fig.9 Measurement errors under asymmetric distribution
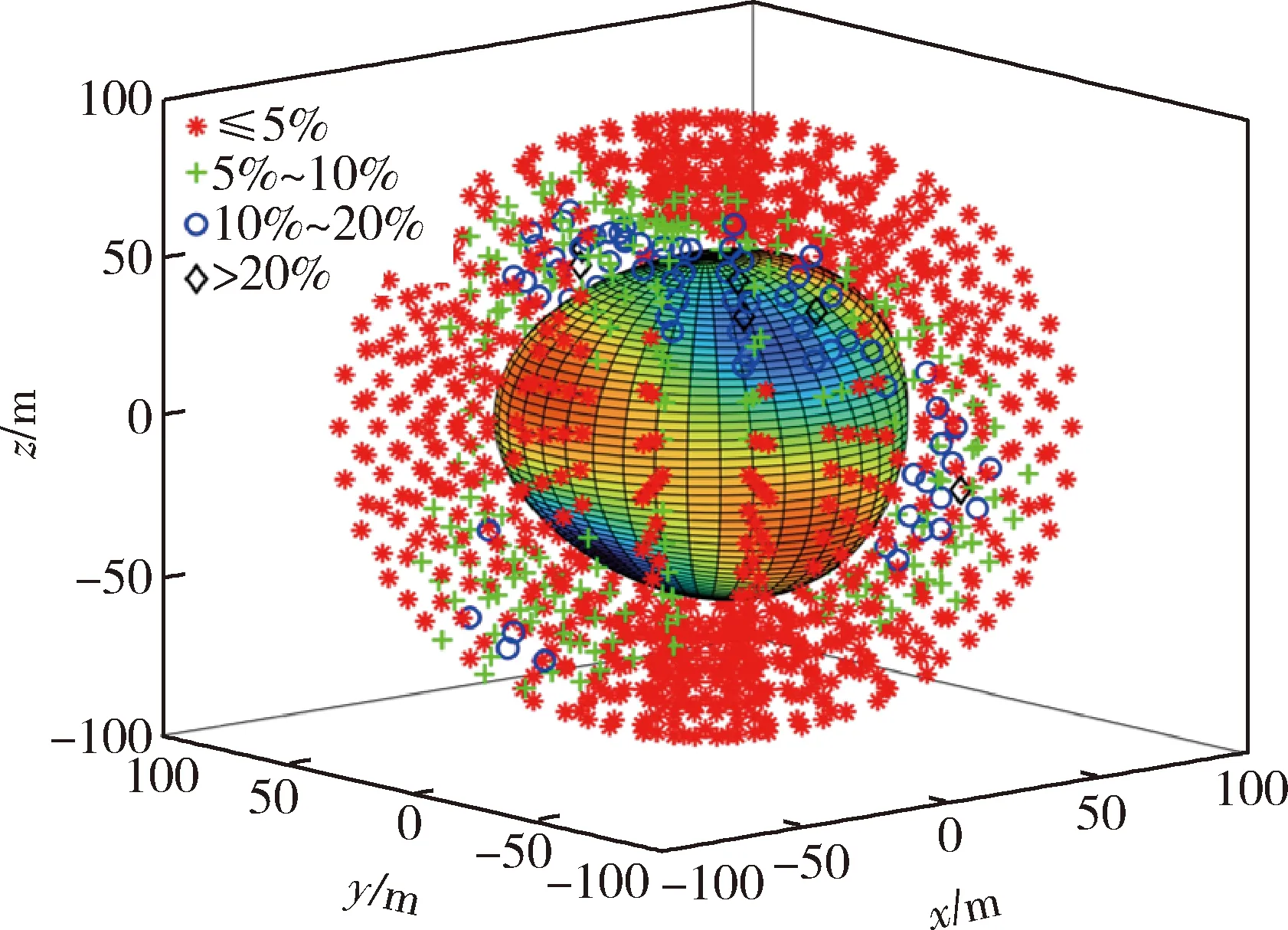
图10 组合轨迹下测量误差Fig.10 Measurement errors under combined trajectory
4.2 引力场测量精度
利用上述仿真校验后的结论,来规划相应的飞行轨迹对一个四阶球谐引力场反演.如前所述,目标小行星的四阶球谐系数参考433Eros设定,但引力常数和其它参数不变;状态参数的标称值、先验值和标准差如表4所示;同样在距离小行星表面30 m左右处给探测器施加速度脉冲,飞行轨迹仿真时间为2 500 s,特征点提取间隔为30 s左右.
根据上述球谐系数可知,若通过均质球体展示,其整体质量应是沿经度方向变化,对比实际的433Eros外形,符合这一理想化结果.以此为标称值的均质不规则球体,其整体质量虽沿经度方向变化,但纬度方向也存在少量质量聚集和缺失;因此可以根据上述轨迹规划方案,选取探测器横向方向轨迹来进行其整体引力测量,此外在高纬度上添加另一条横向飞行轨迹,以此来优化第一条飞行轨迹下的反演结果.两条飞行轨迹如图11所示;四阶球谐系数和引力常数反演结果如表4所示;引力场的整体测量误差如图12所示.

表4 四阶球谐系数标称值、标准差、先验值及估计值Tab.4 Nominal values, priori values, estimated values and standard deviation of the four-degree spherical harmonic coefficients
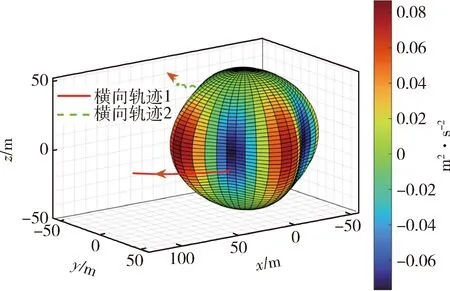
图11 探测器飞行轨迹设计Fig.11 Flight trajectory planning for the probe

图12 引力场测量误差分布Fig.12 The distribution of gravity field measurement errors
从表4的估计结果可知,对于小行星引力常数的估计误差可达到0.2%以内;从图12可知,其整体引力测量误差在5%以内;可见该测量方法对弱引力小行星的不规则引力场测量是可行的,精度较高.
由实验结果可知,对于无绕飞轨道的小半径弱引力目标天体,根据其整体质量分布来规划探测器的飞行轨迹;然后利用自主导航数据可以有效解算其引力常数和全局引力信息.
5 结 论
针对小行星探测任务中不规则弱引力场测量难题,提出一种利用视觉导航数据来对其引力场球谐模型反演的方法.在探测器飞行过程中,利用光学导航相机获取特征点的像素信息,结合其从导航特征库中匹配得到的三维位置坐标,然后通过加权最小二乘批处理算法处理飞行轨迹下的积累数据来估计小行星引力常数和球谐系数;此外讨论了如何根据小行星整体质量分布来规划探测器的飞行轨迹,以利用较少的飞行轨迹下量测数据来完成目标天体的全局引力信息测量.仿真结果表明本方法适用于无绕飞轨道的小半径弱引力目标天体,且适用于密度分布非均匀天体;在充分考虑各种误差条件下,具有较高的测量精度和一定的工程实用性.

