顾及抗差性的GNSS多尺度地壳运动场构建方法

苏小宁，朱庆，孟国杰，孙海丽，闫浩文

1 兰州交通大学测绘与地理信息学院，兰州 730070 2 西南交通大学地球科学与环境工程学院，成都 611756 3 中国地震局地震预测研究所，北京 100036 4 首都师范大学资源环境与旅游学院，北京 100048

0 引言

GNSS(Global Navigation Satellite System)观测技术在研究全球地壳运动和构造活动等方面发挥了重要的作用，“中国地壳运动观测网络”、“中国大陆构造环境监测网络”、首都圈GNSS观测网和省属地震气象测绘部门的CORS(Continuously Operating Reference Stations)网等覆盖全国和区域的多源观测数据，为获取中国大陆较高空间分辨率的变形场提供了丰富的资料(Wang and Shen，2020).由于GNSS速度场相对于某个参考基准，因此选择不同参考基准导致速度场的表现形式差异巨大.而应变率场与参考基准选择无关，通过对比应变积累和地震矩释放的关系，在地震危险性分析和长期预报方面发挥着重要作用(Ojo et al., 2021)，这其中的关键是解算出能反映测站空间不规则分布特征且精准的应变率场.

目前解算应变场的方法可总结为两类：一类是建立块体-断层模型，计算块体内部均匀应变，称为物理模型(申重阳等，2002；Tape et al., 2009)；另一种是利用GNSS速度场，构建空间连续的速度场模型，进而解算应变率场，称为数学模型(Tape et al., 2009).可见，在数学模型中关键是如何精准构建空间连续的速度场模型，常用的方法有距离加权(Shen et al，1996)、多面函数(武艳强等，2009)、Kriging插值(刘晓霞等，2014)、最小二乘配置(江在森和刘经南，2010)和多尺度球面小波(Tape et al., 2009；程鹏飞等，2015；苏小宁等，2016)等，这些方法在确定观测值权重时或将GNSS速度场看作为等精度的观测值，或利用拟合的速度场形式误差表征其不等精度的特征.但实际上经常存在由于观测数据质量较差导致的误差较大或者土层观测点标墩不稳定产生的局部速度差异，也就是在观测数据中存在少量粗差.此时利用现有方法构建速度场模型时，少量粗差将会对解算的应变场产生重要的影响，即上述方法均不具备抗差功能.

本文基于能够体现GNSS测站不规则分布特征的多尺度球面小波方法构建GNSS速度场，获取不同空间尺度的地壳运动场，在此基础上通过抗差迭代算法顾及速度场中存在的少量粗差对建立速度场模型的影响，通过在实测数据中人为加入粗差的模拟计算验证方法的抗差性，结合川滇地区最新的GNSS速度场数据给出了区域的速度场和应变率场模型.

1 基于球面小波算法的多尺度地壳运动场建模

1.1 速度场函数模型

球面上观测点的三维速度可以以南北向、东西向和垂直向3个分量来表示，本文只考虑水平向速度场，因此只涉及到南北向和东西向2个分量，考虑垂直向时的方法与本文所述相同.地面观测站(λ，φ)的地壳运动速度ν(λ，φ)可表示为

(1)

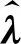
基于球面小波算法构建多尺度地壳运动场模型的本质是采用小波基函数作为估计速度场的框架，利用对小波母函数进行平移和伸缩等仿射变换后得到的小波基函数来表示不同分量的速度场，因此公式(1)可以变换为

(2)

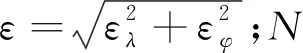
(3)

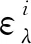
1.2 空间球面小波基函数

以高斯函数差建立的球面小波基函数(Difference of Gaussians，DOG)在构建多尺度地壳运动场模型时得到了广泛应用(苏小宁等，2016)，DOG小波的函数模型为(包伯成等，2009)

(4)

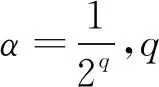
1.3 空间球面小波分解

空间球面小波分解的原则是根据观测站的分布建立一系列球面小波基函数.通过对球面进行三角形分解，可以获得在球面上均匀分布的球面三角形网格，分解的层次与球面小波基函数的尺度相对应，也对应于不同边长的球面三角形，具体形式可参考 Wang和Dahlen(1995).首先根据分解尺度建立空间规则分布的小波基函数，再根据地表观测点的空间密度对规则分布的小波基函数进行筛选，使得最终的小波基函数集在空间分布上与地表观测站的空间密度密切相关，进而构建的模型能够凸显测站不规则分布的特征.分解的具体步骤如下：

(1)选取研究区经纬度的覆盖范围形成球面矩形，计算球面矩形对角线的长度，搜索小于该长度且距离最近的三角形边长，确定最小分解尺度；

(2)根据不同分解尺度，建立多层次且规则分布的空间小波基函数，标注对应的球面三角形边长；

(3)根据地表观测点分布，对所有小波基函数逐个搜索，以小波基函数所在位置为圆心和分解尺度对应的球面三角形边长为半径，确定小波基函数所对应的“空间支撑”范围，统计“空间支撑”内地面观测站的个数，筛选出“空间支撑”内部多于3个站点的小波基函数，获得模型可用的最大分解尺度、空间不均匀分布的小波基函数及其数量；

(4)统计分析不同分解尺度小波基函数的有效覆盖范围，选择有效覆盖范围超过70%的最大分解尺度为最终的球面小波分解尺度，形成在空间不规则分布且不同分解尺度的小波基函数集.

1.4 观测方程病态问题及其最优化解

根据地表观测站的空间分布建立的球面小波基函数个数为N个，因此与其对应的系数，也就是待求参数的个数也是N个，而观测点的个数为M个，也就是观测量个数为M.在实际建立速度场模型时，观测点个数往往小于待求参数个数，导致观测方程的参数求解成为对欠定方程的求解问题.同时，由母函数经过仿射变换得到的DOG小波基函数为非正交基，导致法方程秩亏，涉及到不适定方程的求解问题.

在建立速度场模型时，可以通过最优化算法中的正则化方法，求解出待求参数向量，目标函数和参数的最优解分别为

(5)

m=(GTPDG+λ2I)-1GTPDd,

(6)

式中S(m)为目标函数，通过以目标函数为最小准则获取参数的最优解.G为由小波基函数组成的系数矩阵，m为待求参数向量，d为地表GNSS观测点观测的速度场向量，CD为观测数据的方差-协方差矩阵，其逆矩阵为权矩阵PD，考虑到不同位置测站计算的地壳运动速度为独立观测量，则CD和PD均为对角矩阵.CM为待求参数的方差-协方差矩阵，本文采用Tikhonov正则化方法(徐天河和杨元喜，2003)，CM的具体形式为λ2I，I为单位对角阵，λ为正则化参数.利用公式(6)，通过多次迭代之后，则可以求解出参数m的平差值.可以看出，由于对法方程矩阵的对角元素进行了修正，显然该平差值为有偏估计值.

从公式(6)可以看出，在参数最优解求解的过程中，如果已知基函数分布和最优化解算方法，则参数的解只依赖于如何确定观测数据的权矩阵.以往普遍采用拟合的地表测站GNSS速度场的形式误差给定，但如果在观测数据中存在异常值或者粗差值，利用形式误差确定权矩阵的方法并不能精确地表达其随机特征，此时公式(6)不具备抗差功能，则无法获得精确的参数解，最终建立的速度场模型值得商榷，因此，有必要对公式(6)进行修正，使其具备抗差功能.

2 顾及抗差迭代算法的多尺度地壳运动场模型构建

一个好的估计方法不仅要具有“稳健性”，还得具有“抗干扰性”.“稳健性”是指当假定模型与实际模型有微小差异时，其估计方法的性能只受到微弱的影响；“抗干扰性”是指当观测样本中混入少量粗差时，估计值受到的影响不大(杨元喜等，2002).地表不规则分布的地壳运动速度场属于独立观测，且不等精度，适合采用按等价权原理作抗差估计，目的是解决不等精度独立观测值权函数的确定问题(周江文，1989；杨元喜，1994).

2.1 顾及抗差性的最优化算法原理

在公式(5)所示最优化算法的目标函数中，第一项为观测数据残差的加权平方和，显然个别异常大残差的出现会导致平方和显著增大.为了达到平方和最小的目标函数，平差值必然会迁就那些异常观测值或者粗差值，使得平差值偏离最优值，因此个别异常值或粗差会对整个估值产生较大的影响.抗差估计的本质是利用增长较慢的函数代替平方和函数，得到具有较好抗粗差性的估值.

(7)

2.2 顾及抗差性的迭代最优化算法实现步骤

(1)确定待估参数的初值，确定权矩阵的初值，给出观测数据的方差-协方差矩阵；

(2)按照公式(5)和公式(6)所示的传统最优化算法估计参数的平差值，计算观测数据与模型值的残差；

(5)对参数平差值与初值的差值进行评价，如果其符合限差要求，则结束求解；否则重复步骤(2)—(4)进行迭代求解，直至待求参数平差值的差值符合要求为止.其中第k+1次的迭代解为

(8)

3 川滇地区地壳运动场模型

3.1 多源数据融合的川滇地区GNSS震间速度场

中国大陆观测地壳运动的GNSS测站主要来自于中国大陆构造环境监测网络，该网络包括260个连续观测站和2000个流动观测站，其中32个连续观测站和1056个流动观测站观测起始于1998年，其余测站观测起始于2009年，所有的数据均已经获得了超过10年的观测资料.除此之外，在一些地震活动性较强的区域，例如首都圈地区、山西地堑带和川滇地区等，也进行了GNSS流动观测网的加密观测；省属的地震、气象和测绘部门为了满足区域性CORS网的需求，在所属范围也布设了连续观测站，这些测站中的一部分能够满足地壳运动观测的需求.Wang和Shen(2020)对以上数据进行了收集和整理，同时也收集了中国大陆周边的GNSS观测资料，通过高精度数据处理与震间形变场提取，给出了中国大陆高空间分辨率的GNSS震间速度场.数据处理采用GAMIT/GLOBK软件(Herring et al., 2015, 2018)，所有数据解算采用统一的策略，确保解算的坐标参数的高精度和强自洽性.在GNSS原始观测数据解算阶段，将地面测站坐标、地球定向参数(极移和协调时间时)和卫星轨道一并估算，有效地消除了由于地球物理模型或者轨道参数变化所带来的系统性偏差(Wang and Shen, 2020).在时间序列建模阶段，同时考虑了大地震同震和震后位移的影响；考虑到不同天线类型和可能的天线设置误差，对GAMIT给出的测站坐标误差进行了重新分配，并利用有色噪声随机模型构造观测数据的方差-协方差矩阵，体现出时间序列中的时间相关性特征(Tao et al., 2021).

在Wang和Shen(2020)给定的GNSS速度场中，中国大陆构造环境监测网络的数据截止于2015年，本文采用与其一致的观测数据解算策略、时间序列建模策略和地壳运动解算策略，补充处理了该观测网2017、2018、2019和2020年的观测数据，增加了观测数据的长度，也提高了速度场的稳定性，更新的川滇地区GNSS速度场如图1所示.

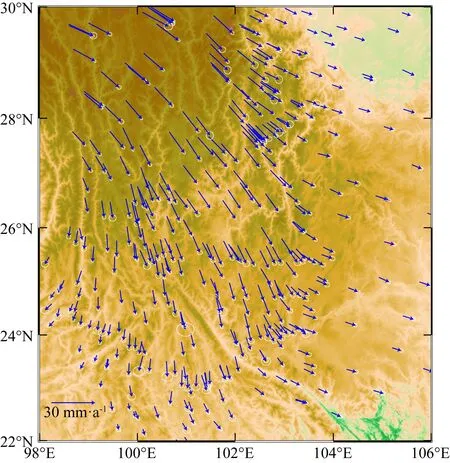
图1 川滇地区相对于欧亚参考框架的GNSS速度场，误差椭圆置信区间为95%Fig.1 GNSS velocity field with respect to Eurasian reference frame in the Sichuan and Yunnan regions. The confidence interval of error ellipse is 95%

图2 川滇地区GNSS测站分布的球面小波分解尺度Fig.2 Decomposition scale of spherical wavelet based on the distribution of GNSS stations in the Sichuan and Yunnan regions

3.2 基于球面小波算法的多尺度地壳运动场模型

根据GNSS测站分布，依据空间球面小波分解原则，获得川滇地区的球面小波分解尺度，如图2所示.研究区内最大分解尺度的最小值为6，最大分解尺度的最大值为9.除西南角和东南角的边缘区域，其他区域的最大分解尺度均在7以上.最大分解尺度能达到9的区域主要沿着主要构造带分布，例如小江断裂带南端、红河断裂与丽江—小金河断裂交汇的区域和鲜水河断裂与龙门山断裂南端交汇的三岔口区域.川滇菱形块体覆盖的主要区域最大分解尺度都能达到8，因此本文最终选择的最大分解尺度为8，分解尺度的选择范围为3～8.

正则化参数的求解采用留一交叉验证法(Leave-one-out Cross Validation，LOOCV)，首先去除一个观测点数据，计算待求参数，然后计算该点观测值与模型估值之间的差值，通过全局搜索，选择出最优的正则化参数，进而求解出待求参数的最优解,正则化参数的搜索过程如图3所示.选择1～1010作为搜索范围，可以看出该过程搜索到了函数的全局最小值，进而提取出正则化参数λ的取值，图3中横坐标取正则化参数λ的常用对数，其在东西分量和南北分量分别为533和849.

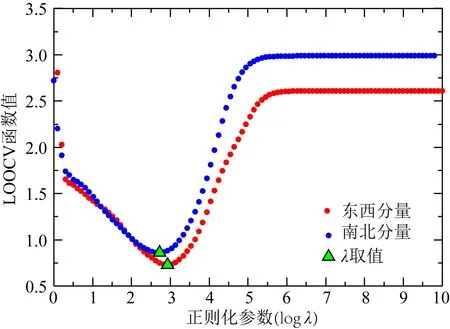
图3 基于LOOCV算法的最优化算法正则化参数Fig.3 Selection of regulation parameters based on optimized LOOCV method

确定球面小波分解尺度和正则化参数之后，通过多次迭代即可求解出待估参数的最优化值，进而正演出研究范围内空间任意一点的地壳运动速度，实现地壳形变场建模，给出空间连续的地壳运动图像，如图4所示，图中冷色(蓝色)代表小速率值，暖色(红色)代表大速率值.可以看出，安宁河—则木河—小江断裂组成的构造带是川滇菱形块体地壳运动速率的分界带.

图4 川滇地区地壳运动场模型(a) 东西分量; (b) 南北分量.Fig.4 Crustal deformation model in the Sichuan and Yunnan regions(a) The EW component; (b) The NS component.

3.3 顾及抗差迭代算法的多尺度地壳运动场模型

抗差迭代算法可有效削弱异常观测值和粗差对地壳形变场建模的影响，进而获得准确的应变率场.通过多次抗差迭代计算，在所有参与建模的367个GNSS测站中，检测出74个降权观测值，占比为20%，检测出7个除权观测值，占比为2%，图5中蓝色三角形站点为正常观测站点，黑色三角形站点为降权观测站点，红色三角形站点为除权观测站点.

图5 抗差迭代算法给出的川滇地区三类GNSS测站分布图Fig.5 The distribution of three types of GNSS stations in Sichuan and Yunnan regions based on robust iterative algorithm

图6给出了利用抗差迭代算法对部分测站进行降权和除权之后，基于多尺度球面小波算法构建的川滇地区地壳运动场模型，可以看出考虑抗差性前后计算的速度场空间分布形态基本一致，安宁河—则木河—小江断裂是川滇菱形块体的东边界这一基本特征未发生明显改变.为了进一步分析抗差迭代算法在构建地壳形变场时的作用，对本文顾及抗差性的方法与传统多尺度球面小波方法获得的地壳运动场模型进行对比，结果如图7所示，图中也给出了降权站点和除权站点的分布.可以看出，二者差异的量值在1.0 mm·a-1以内，说明虽然在构建速度场模型时考虑了抗差性，但由于原有速度场本身数据质量较好，因此得到的结果是稳定的，二者的差异较小，而差异性较大的区域总是覆盖着被降权或者除权的测站.

4 讨论

4.1 GNSS速度场中存在粗差测站的原因

利用目视法对基于GNSS观测资料解算的中国大陆地壳运动场进行分析，发现不可避免地存在一些与周围测站的运动特征明显不协调的测站.其产生的原因主要包括：(1)因观测时间跨度太短而无法拟合出真正的震间运动；(2)观测标墩建于土层之上，由于季节变化等因素导致标墩本身存在非线性的变化；(3)测站观测环境的改变导致观测噪声增加或运动特征偏离真值.

本文所采用的观测数据均超过了10年，超过解算震间变形时对时间跨度4.5年的要求(Blewitt et al., 2013).观测环境的改变在测站的日志文件中都会有明确记载，在数据预处理阶段已经被考虑到.因此，为了分析测站被降权处理和被除权处理的原因，本文重点对这些测站的观测标墩和数据质量进行了进一步分析.其中测站标墩分为基岩点和土层点，通常认为基岩点能够精准代表地壳的运动特征，而土层点会受到土壤随着季节变化的热胀冷缩和土层本身不稳定等因素的影响(谭伟杰等，2017)，产生局部效应而可能无法精准代表地壳的运动特征.被降权和除权处理的81个站点全部为土层站点，可见观测结果中存在明显的局部影响.通过观测数据形式误差的大小体现出数据质量的差异性，分析权不变、降权和除权三类测站形式误差的差异性.计算三类数据东西向和南北向形式误差的均值，权不变、降权和除权三类数据东西向形式误差的均值分别为0.61、0.70和0.93 mm·a-1，南北向形式误差的均值分别为0.52、0.60和0.83 mm·a-1，可以看出三类数据的形式误差存在差异，表明其时间序列的离散度逐渐增大，数据质量逐渐降低.

图6 顾及抗差迭代算法的川滇地区地壳运动场模型(a) 东西分量; (b) 南北分量.Fig.6 Crustal deformation model in Sichuan and Yunnan regions considering robust iterative algorithm(a) The EW component; (b) The NS component.

图7 顾及抗差迭代算法与传统方法构建的地壳运动场在东西分量的差值Fig.7 The difference of crustal deformation model in the EW component between our and traditional method

4.2 抗差迭代算法的抗差性分析

为了进一步检验抗差迭代算法的抗差性能，在速度场空间变化较大的川滇地区人为地引入粗差，分析粗差引入前后速度场模型的差异性特征.引入粗差的方式有在单个测站引入粗差和在相邻的几个测站引入粗差两种，具体如图8所示，其中测站H335、H387和H380为3个在区域上独立的含有粗差的测站，测站H346、H111、H112、SCYY和H103为在区域上具有相关性的5个含有粗差的测站.用含有粗差的测站构建运动场模型，并与不含粗差的数据构建的结果进行对比，分析本文算法的抗差性.

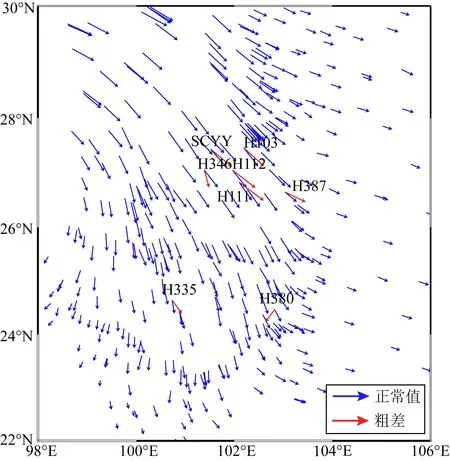
图8 速度场中单个测站和区域测站加入人为误差的两种方案Fig.8 Two schemes of adding gross errors artificially of individual station and regional stations in velocity field

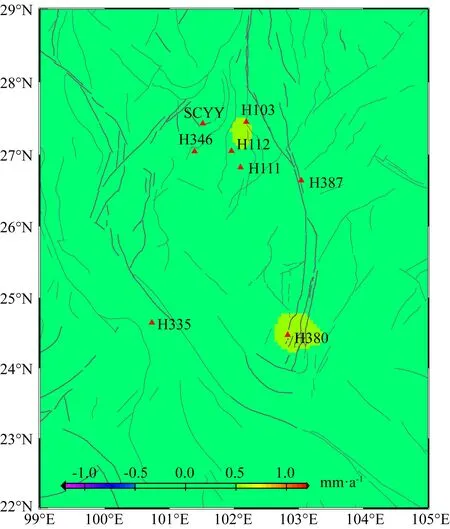
图9 加入人为粗差前后东西向速度场模型的差异分布Fig.9 The difference of crustal deformation model in EW component before and after adding gross errors artificially

图9给出了对二者速度场求差的结果，图中-0.5～0.5 mm·a-1以内的值用同一个色标表示，可以看出，其中测站H335和H387两个单独的存在粗差的测站经过抗差迭代算法之后，对建模的结果并未产生影响，而另一个独立的H380测站的粗差却对建模结果产生了明显的影响，进一步对测站分布分析可以看出，在H335和H387两个测站10 km以内的范围还有其他测站，而H380测站在10 km以内的范围内没有其他测站，也就是说抗差迭代算法从测站H335和H387检测出了粗差，而从H380测站没有检测到粗差，把含有粗差的观测值当作好的观测值对待，这是由于该测站周边没有其他观测站作为对比，即便其本身含有粗差也被当做了有效值.由测站SCYY、H346、H103、H111和H112等5个测站组成的含有粗差的区域对建模结果也产生了明显的影响，表明区域性存在的粗差会对建模结果产生影响.

4.3 抗差迭代算法对解算应变率场的贡献

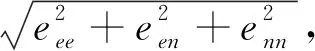
从图10可以看出，川滇地区重要应变积累的区域沿着主要的活动构造带分布，其中主要的一个条带是安宁河—则木河—小江断裂带，这也是川滇菱形块体的东边界，红河断裂与丽江—小金河断裂交汇的区域是另外一个重要的应变积累区域，该分布特征与已有的研究成果保持一致(Qu et al., 2018)，但在应变集中区的量值上普遍高于已发表的结果(Pan and Shen, 2017；李长军等，2019)，这主要是由于本文采用的多尺度球面小波的应变计算方法能够凸显出测站不均匀分布的特征，获取不同空间分辨率的应变率场，进而提取出应变积累的集中区域.图10也给出本文方法与传统多尺度球面小波方法解算的应变率场的差异，从第二不变量的量值来看，应变差异值的量值远低于应变的量值，表明两个结果均是稳健的，对比图10和图7可以看出，应变率差异较大的区域也是速度场差异较大的区域，同时也是存在被降权或除权测站的区域.

4.4 川滇地区多尺度应变积累特征

基于多尺度球面小波算法解算应变率场的优点之一是能够获取不同空间尺度的应变率场，从而体现出不同规模构造运动的应变积累特征.小的分解尺度能够获取大规模构造运动的应变积累，例如块体边界的应变积累；大的分解尺度能够获取小规模构造运动的应变积累，例如块体边界应变积累的差异性分布或块体内部次级断层的应变积累.图11分别给出了分解尺度为3～7和8的应变率第二不变量，二者之和为区域的总应变，总体特征与已有结果保持一致(Jin et al, 2019; Zhang et al., 2019).从分解尺度为3～7的应变率场可以看出，应变积累的主要区域为块体运动的边界区域，作为川滇菱形块体东边界的安宁河—则木河—小江断裂带，其是川滇地区主要的应变积累区域，其中以安宁河断裂和则木河断裂为东边界的大凉山次级块体内部存在应变积累，沿着小江断裂的应变积累穿过红河断裂之后一直向西南方向延伸.其他主要的应变积累区域是位于红河断裂与丽江—小金河交汇的区域和中缅边界的几条西南向断裂分布区域，主要包括畹町断裂和南汀河断裂等.分解尺度为8的应变积累分布显示区域内除了沿着主要断裂的应变积累外，还存在局部小区域的应变积累，这些应变积累主要体现了沿着断裂应变积累的差异性特征.

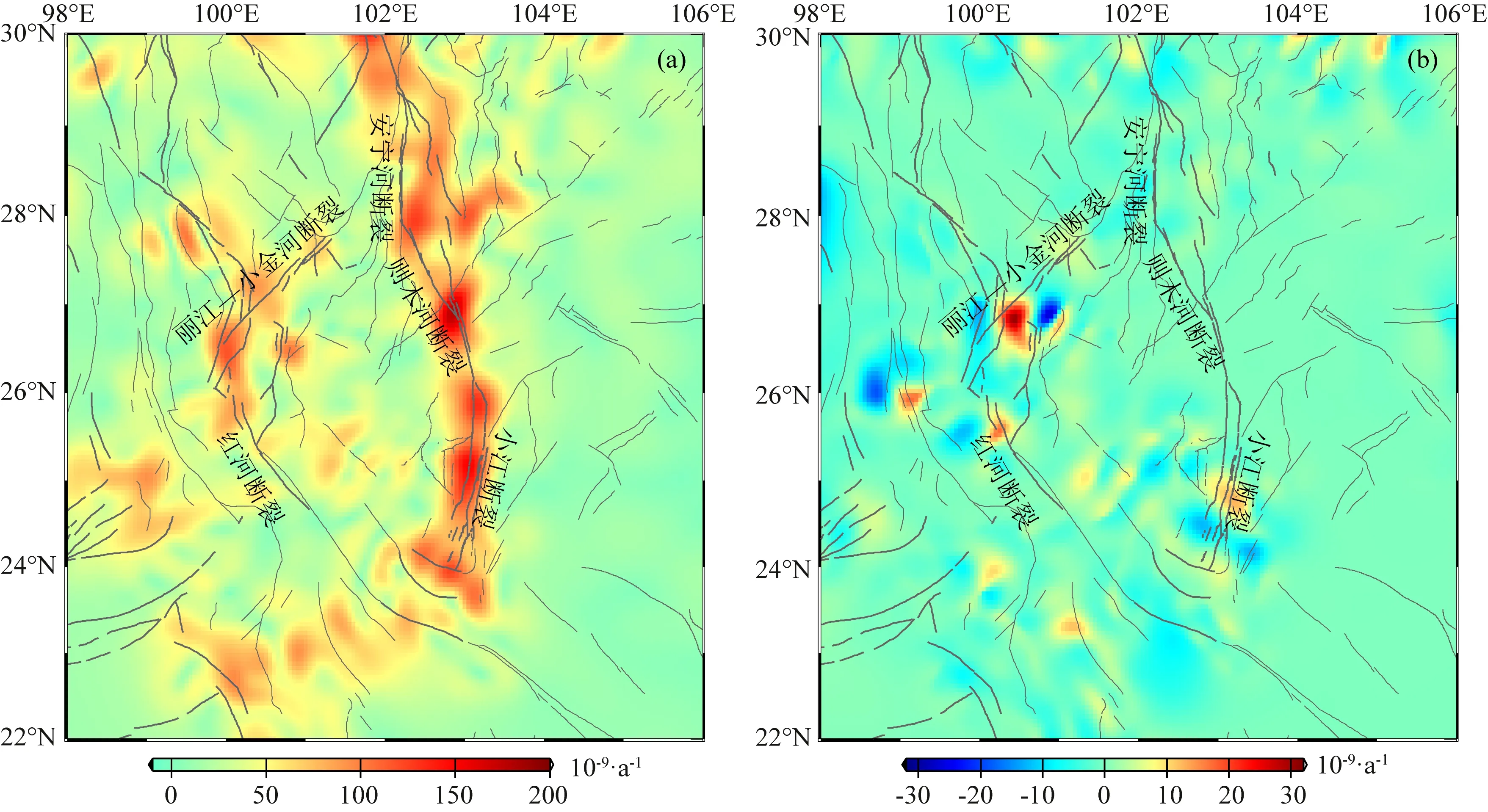
图10 川滇地区应变率第二不变量(a) 本文方法解算的应变率场; (b) 本文方法与传统多尺度球面小波方法解算结果的差异.Fig.10 The second invariant of strain rates in Sichuan and Yunnan regions(a) The strain rate field calculated by our method; (b) The difference between our and traditional method.

图11 川滇地区应变率第二不变量(a) 分解尺度为3～7; (b) 分解尺度为8.Fig.11 The second invariant of strain rates in Sichuan and Yunnan regions(a) The decomposition scale is from 3 to 7; (b) The decomposition scale is 8.

5 结论

利用长期积累的GNSS观测资料经过高精度统一数据处理提取地壳运动图像，然后解算GNSS应变率场，进而对应变积累与地震矩释放进行对比分析，这些是开展区域地震危险性分析的主要工作，并在实际地震潜势研究中得到了广泛应用和验证.由于GNSS时间序列中存在与长期构造运动无关的信息致使拟合的速度场无法真实表达实际的震间地壳运动特征，进而影响到应变率场的结果.

本文提出了顾及抗差性的速度场模型构建方法，考虑到了测站因局部运动和数据质量较差在速度场中产生的粗差.以解算的川滇地区最新GNSS观测资料为例，在观测的速度场中检测出了20%的降权测站和2%的除权测站，对这些测站进一步分析发现，粗差产生的原因是由于观测数据质量较差和测站为土层观测点而存在局部非构造变形，进而获得稳健性较好的速度场模型.通过在观测数据人为加入粗差检验本文方法的抗差性，结果表明单个存在的粗差对速度场模型不会产生影响，而区域性存在的粗差会对结果产生影响，表明本文的方法具有好的抗差性.本文进一步分析了顾及抗差性算法对解算应变率场的贡献，进而给出了川滇地区精准的应变率场.

致谢感谢中国地震台网中心提供的中国大陆构造环境监测网络GNSS观测数据.