盆地沉积结构对地震波初至走时的影响

李佳欣，王赟，杨春

中国地质大学(北京)，地质过程与矿产资源国家重点实验室，多波多分量研究组，北京 100083

0 引言

不论是被动源的天然地震，还是主动源的勘探地震，都受到震源、传播介质以及观测点处局部场地条件的影响(Aki and Richards，1980).其中，天然地震震源定位、震级的确定，尤其对于浅源地震，更是与传播介质和场地效应密切相关(Anderson et al.，1986；Scrivner and Helmberger，1994；Abercrombie，1997)，盆地或局部沉积结构对地震波传播运动学和动力学特征的影响不可忽略.为此，研究者对于场地效应产生的地面震动时频畸变，从而影响评估地震风险，重要基础设施的规划和设计关注已久(Poceski，1969；Bravo and Sánchez-Sesma，1990)，分别从土层和局部地形两个方面开展了大量的研究(Mossessian and Dravinski，1990；Azarbakht et al.，2014；张宁等，2017).其中，土层效应研究主要集中于软弱沉积物性差异、互层结构和厚度以及基岩形态对地震波的放大作用(黄妍等，2007；张立，2012；Denolle et al.，2014；孙天为，2019).在一些山间小盆地和沟峡冲积扇中，浅层松散沉积所引发的场地效应可能与下伏沉积层(基岩)相互作用，叠加局部地形影响，产生更复杂的地震波畸变作用(Bard and Bouchon，1985；Kawase and Aki，1989；刘启方，2021).

利用天然地震研究地球深部结构及其动力学过程是地震学的主要工作之一.在天然地震和地球深部动力学研究中，一般将上地壳分为两个亚层，分别是上部的沉积层和下部的结晶基底(滕吉文等，2008，2014；任隽等，2012)；且对于大尺度的壳幔结构研究，一般假设这两层介质为各向同性层或速度梯度递增层(熊绍柏等，2002；张家茹等，1998；董治平和张元生，2007；滕吉文等，2014).随着地震和深部动力学研究的深入，研究者很早就认识到上地壳沉积层的速度结构是研究深部构造的基础，对壳幔深部震相的解释具有重要意义(赵俊猛等，2003；滕吉文等，2014).Hauksson等(1987)通过地下两个深度和地面共计三个水平梯度面上的三分量地震观测，分析了近震在走时、波形、能量和频谱上随深度的递减所呈现的变化规律，厘定了沉积结构和场地效应对地震波传播的影响.王凤贤等(1999)发现盆地内地震台记录的近震数据在确定发震时刻时存在滞后现象，具体表现为记录地震的井下摆深度越大，滞后时间越小；台站越靠近盆地中心，滞后时间越大；从而可能造成震源定位时深度偏大(刘渊源等，2011).此外，沉积盆地对震相波形的影响也会给地震定位带来较大误差(董一兵等，2018；Dong et al.，2018).Owens 等(1987)和薛光琦等(1999)认为地震PKP震相走时的变化主要归因于Moho面的起伏，但沉积结构的影响不可忽略；张子琦等(2018)通过研究发现，当地震台站位于沉积层上时，忽略低速沉积层会使莫霍面预测深度增大约2km；郑德高和李志伟(2014)通过分析地震观测数据，发现上地壳沉积层与结晶基底之间形成的多次波会影响到其他震相的识别，从而给深部壳幔结构的研究带来困难.此外，沉积层的成层性表现出的弹性各向异性对地下结构研究和震源定位的影响也引起了行业的重视(Brittan et al.，1995).

由于沉积盆地内部相对稳定，很少产生大震级的地震，因此盆地内固定台站较少，台网分布也较为稀疏(孙天为，2019；王向腾等，2021)，这对地震定位十分不利.以2016年Oklahoma州的MW5.1地震为例，由于该地区台站分布稀疏，不同学者得到的地震起始破裂深度定位结果差异可达3 km(Yeck et al.，2016；Goebel et al.，2017).此外，低频的天然地震信号可能对尺度较小的沉积层速度结构不敏感(Nunziata et al.，2009)，但作为地震传播的介质，盆地的影响对地震观测不容忽视(Pratt，2003；Dong et al.，2018).近些年发展的背景噪声成像(Campillo and Paul，2003)、H/V法(Agostini et al.，2015；谢晓峰等，2007；Vella et al.，2013；Langston et al.，2009；Civico et al.，2017)、井下观测(Hauksson et al.，1987；Abercrombie，1997；Satoh，2006；Yamada and Horike，2007)以及双差法(Zhang and Thurber，2003，2006)都说明了浅层速度结构研究的重要性(吴海波等，2018).尤其近些年盆地内中小震频发，不论是讨论这种地震产生的地应力异常天然背景还是压裂诱发(Farahbod et al.，2015；陈秋玉，2021)，沉积盆地结构对浅源地震三参数反演的影响成为领域关注的热点(Lomax and Savvaidis，2019).

盆地沉积层往往呈层状展布，且为细密的分层结构，其精细结构可通过测井数据获取.但受限于成本及地质条件，在大多数地区其沉积层精细结构无法获取.此时，沉积层的细密分层结构往往由等效的各向同性厚层替代(郭乃川等，2012).但这种替代带来的误差尚未有研究人员进行过深入分析，而这或许正是目前浅源地震深度定位不准的原因所在.此外，天然地震产生的低频地震波在穿过由薄层组成的沉积层时会产生长波长效应，即沉积层会表现出视各向异性的性质，对地震波的运动学和动力学特征产生影响.本文选取塔中盆地沉积层作为研究对象，分析其在进行各向同性等效和长波长等效(VTI近似)后初至波产生的走时误差，并讨论了不同震源深度、不同震中距时不同等效方法的适用性条件.

1 理论基础

1.1 沉积模型

不论在陆地还是海域，上地壳广泛分布沉积盆地或克拉通(常子恒，2001).除了山前带附近和盆地内部存在的局部地层倾斜或波状起伏，在不考虑断裂构造和微尺度割理、端理、裂缝隙影响时，这些沉积盆地大多数可用均匀各向同性水平层状介质组成的互层结构近似.如图1所示为我国最大的内陆克拉通盆地——塔里木盆地塔中某井的声波、密度测井曲线和根据钻孔取芯以及测井解释获得的岩性柱状图.显然，不同岩性地层具有不同的速度和密度，且相互叠置形成了精细分层的层状介质.在地震学研究领域，一般可以将之抽象为图2b所示的水平层状模型.

1.2 均匀各向同性等效

(1)

其中，

(2)

为各层厚度与总厚度之比.显然，任意给定一个水平层状介质模型，均存在一个等效的单层介质可与之近似，从而可以把具有4N个参数的复杂模型简化为只需要四个参数表征的简单模型，这是简单的各向同性等效或称ISO(isotropy)等效，其对应模型下文中简称ISO模型.

1.3 VTI近似

当层状介质中传播的地震波波长远大于层厚时，层状介质会呈现一定的各向异性特征.因此，Backus(1962)给出了VTI(transverse isotropy with a vertical symmetry，具有垂直对称轴的横向各向同性介质)近似公式；进一步利用Levin(1979)给出的层状介质与VTI近似弹性参数的换算关系，以及Thomsen(1986)给出的三个各向异性参数定义，可将VTI近似表示为

(3)

其纵、横波垂向速度为

(4)

其中，

图1 塔中某井声波、密度测井曲线与解释井柱蓝线为声波时差曲线，红线为密度曲线，最右侧为钻孔柱状图.Fig.1 Acoustic and density logging curves, interpretation well string of a well in TazhongThe blue line and the red line indicate the acoustic and density logging curves, respectively. On the far right is the boring log.

(5)

式中，Cij为近似介质的弹性系数，符号“〈〉”表示平均运算，vP、vS、ρ分别为层状结构内单层的纵、横波速度及密度.即利用两个速度参数、密度和三个各向异性参数，即可将N个水平层叠置的互层结构表征为VTI介质(张中杰等，1990；王赟等，2018; 王赟和杨春，2019；李佳欣等，2021)，如图2c所示；一般称之为VTI近似，其对应模型下文中简称VTI模型.

图2 水平层状介质模型(Layer模型)与对应的ISO等效模型、VTI近似模型(a) ISO模型； (b) Layer模型； (c) VTI模型. vPi、vSi、ρi、hi分别表示Layer模型中第i层的纵、横波速度、密度和厚度，N表示互层数量；分别表示ISO模型的纵、横波速度和密度；分别表示VTI模型的纵、横波垂向速度和密度；ε、γ、δ分别表示VTI模型的Thomsen参数.Fig.2 Horizontal layered model and corresponding isotropic equivalent model, VTI approximate model(a) ISO Model; (b) Layer Model; (c) VTI Model. The velocity of P-wave and S-wave, density, thickness in Layer Model are represented by vPi, vSi, ρi and hi, respectively. The velocity of P-wave and S-wave, densityin ISO Model are represented by VP, VS and respectively. Thevertical velocity of P-wave and S-wave, density in VTI Model are represented by VP0, VS0 and respectively. Thethomsen parameters in VTI Model are represented by ε, γ, and δ, respectively.

2 建模与模拟

2.1 建模

塔里木盆地的Moho面深度在40～50 km之间，地震多发生在周缘的天山造山带与西昆仑盆山结合部西南缘和西北缘，以构造带、中上地壳浅源地震为主，鲜有下地壳和软流圈的地震，且频次最高值出现在20 km深度左右(Zhao et al.，2003；雷显权等，2012；李涛和王宗秀，2005)；盆地内活动断裂或隐伏断裂诱发地震数量较少，震源深度一般为5～6 km(徐锡伟等，2006).此时，沉积盆地细密分层结构对地震波速度的影响至关重要，进而影响震源深度的定位.由测井数据得到的沉积盆地速度结构，是弹性波在一定频率下所反映的结果，具有尺度效应，即测井数据的采样间隔会影响沉积盆地的速度结构.以我国最大的内陆盆地——塔里木盆地为例，对塔中某井的速度和密度曲线(原始数据采样间隔5 m)以不同间隔(以10 m、50 m、100 m为例)进行平均(式(1))重采样，得到不同间隔的重采样测井曲线如图3所示.

图3 塔中某井纵、横波速度与密度的重采样曲线(a) 纵波速度； (b) 横波速度； (c) 密度.Fig.3 Resampling curves of P- and S-wave velocities and density well logging in Tazhong oilfield(a) P-wavevelocitiy; (b) S-wave velocity; (c) Density.

重采样后可得到总厚度不变，单层厚度(采样间隔)变化的等厚度水平层状模型.将其速度模型和密度模型进行整体ISO等效和VTI近似，计算得到不同采样间隔对应的ISO和VTI等效参数，如图4和图5所示.对于ISO等效模型，由于其等效计算方法与重采样的平均方法相同，采样间隔的变化对等效纵、横波速度和等效密度无影响(图4).对于VTI近似模型，其纵、横波垂向速度在500 m采样间隔内呈缓慢增大的趋势，即采样间隔的变化对近似得到的速度影响较小，相对于原始测井数据采样间隔不超过1%；采样间隔超500 m后，近似速度呈快速增大的趋势，即单层厚度过大会导致近似速度偏大.这说明采用上述平均方法进行重采样，当得到的水平层状模型中单层厚度控制在500 m以内时，进行VTI近似得到的速度较原始测井数据变化较小；但单层厚度较大时，近似速度的偏离较大(图5).对于VTI近似得到的Thomsen参数，ε在500 m采样间隔内基本无变化，相对于原始测井数据采样间隔不超过5%；γ和δ呈向零值靠近的趋势，但在采样间隔300～500 m范围内趋于不变，相对于原始测井数据采样间隔分别不超过24%和36%.即单层厚度在500 m以内时，层厚对ε基本无影响，但对γ和δ影响相对较大.当采样间隔超过500 m时，ε、γ和δ均呈快速向零值靠近的趋势，如图6所示.可见测井数据不同采样间隔对ISO模型的等效速度和密度无影响；但对VTI模型，属强各向异性介质，采样间隔增大除对等效密度无影响外，等效速度逐渐增大，各向异性参数向0趋近.

图4 各向同性等效纵、横速度和密度随采样间隔(深度域)的变化(a) 纵波速度； (b) 横波速度； (c) 密度.Fig.4 Variation of isotropic equivalent P-wave, S-wave velocity and density with sampling interval (depth domain)(a) P-wavevelocitiy; (b) S-wave velocity; (c) Density.

图5 VTI近似垂向纵、横波速度和密度随采样间隔(深度域)的变化(a) 纵波垂向速度； (b) 横波垂向速度； (c) 密度.Fig.5 Variation of VTI approximate vertical velocity of P-wave, S-wave and density with sampling interval (depth domain)(a) Vertical velocitiy of P-wave; (b) Vertical velocity of S-wave; (c) Density.

图6 VTI近似各向异性参数随采样间隔(深度域)的变化Fig.6 Variation of VTI approximate anisotropic parameters with sampling interval (depth domain)

为简化问题，以地震地质综合解释建立的模型作为塔里木盆地沉积层的典型模型(Lomax and Savvaidis，2019)，如图7所示.其中，沉积层内单层厚度各不相同(300～530 m)，可视为图3测井曲线的特例.设模型长度100 km，深度12 km，沉积层厚度6.24 km，介质参数见图8，以讨论中浅源地震为主.假设震源和观测台站均位于盆地中，在模型左侧布设震源，震源深度范围3～12 km，间隔为1 km(图7).为模拟不同深度的天然地震，将沉积层内地震视为浅源地震，震源深度3～6 km；将沉积层下结晶基岩内的地震视为中源地震，震源深度7～12 km.震源频率取1 Hz，此时沉积层内任一单层厚度满足薄层条件(λi/di>4).图8为图7模型对应的纵、横波速度和密度测井曲线，它是在参照地质分层的基础上，由原始测井曲线非等间隔重采样获得，沉积层下的上地壳厚层介质参数参考张家茹等(1998)的结果.

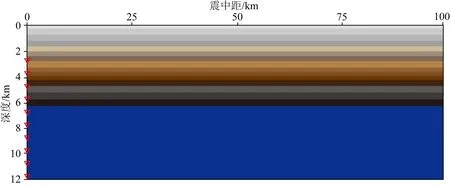
图7 塔中盆地沉积层一维模型红色三角形为不同深度震源.Fig.7 1-D model of sedimentary layer in Tazhong basinThe red triangles represent the sources in different depths.

图8 塔中盆地沉积层对应速度、密度模型(a) 速度模型； (b) 密度模型.Fig.8 The velocity model and density model for the sedimentary layer of Tazhong basin(a) Velocity model; (b) Density model.

在沉积层内单层满足薄层条件的基础上，根据不同的震源深度分别对其进行ISO等效和利用Backus等效理论进行VTI近似，得到对应的等效速度和各向异性参数(图9).对于ISO等效和VTI近似模型，当震源位于沉积层内(<6.24 km)时，上覆介质模型参数随震源深度增大而变化；当震源位于沉积层下(>6.24 km)时，上覆介质模型参数不再变化.

图9 ISO模型和VTI模型在不同震源深度时对应的等效速度及各向异性参数(a) ISO模型和VTI模型的等效速度； (b) VTI模型的各向异性参数. VP-ISO、VS-ISO和VP-VTI、VS-VTI分别表示塔中一维模型对应的ISO模型和VTI模型的等效纵、横波速度；VP-ISOlog、VS-ISOlog和VP-VTIlog、VS-VTIlog分别表示塔中测井数据对应的ISO模型和VTI模型的等效纵、横波速度；ε、γ、δ和εlog、γlog、δlog分别表示塔中一维模型和塔中测井数据对应的VTI模型的Thomsen参数.Fig.9 The equivalent velocity and anisotropy parameters of ISO and VTI model for different depths of sources(a) Equivalent velocities of ISO Model and VTI Model; (b) Anisotropy parameters of VTI Model. VP-ISO, VS-ISO, and VP-VTI, VS-VTI represent the equivalent P-wave and S-wave velocities for the ISO and VTI models corresponding to the 1D model in Tazhong, respectively. VP-ISOlog, VS-ISOlog and VP-VTIlog, VS-VTIlog represent the equivalent P-wave and S-wave velocities for the ISO and VTI models corresponding to the logging data in Tazhong, respectively. ε, γ, δ and εlogging, γlogging, δlogging represent the thomsen parameters for the VTI models corresponding to the 1D model and the logging data in Tazhong, respectively.

2.2 模拟

以Layer模型及对应的ISO模型和VTI模型为正演模型，进行有限差分波场模拟，从而得到三个模型中震源深度不同时不同震中距观测的地震波初至走时.将Layer模型作为参考模型，研究近似的ISO模型和VTI模型对地震波走时产生的影响.ISO模型和VTI模型相对于Layer模型的走时相对误差(下文称误差)为

(6)

(7)

其中，tLayer、tISO和tVTI分别为对应模型的走时.数值模拟得到两种模型假设产生的误差如图10和图11所示.

图10 ISO模型和VTI模型的走时相对误差(a) 震源位于沉积层内； (b) 震源位于沉积层下.Fig.10 Relative error oftraveltime for ISO Model and VTI Model(a) The sources are located within the sediments; (b) The sources are located below the sediments.

图11 走时相对误差二维分布图(a)、(b) 分别为震源位于沉积层内的ISO模型、VTI模型； (c)、(d) 分别为震源位于沉积层下的ISO模型、VTI模型； (e)、(f) 分别为震源位于沉积层内和沉积层下的ISO模型和VTI模型走时相对误差之差.Fig.11 2-D distribution diagram for relative errors of traveltime(a), (b) are the ISO model and VTI model when the sources are located within the sediments, respectively. (c), (d) are the ISO model and VTI model when the sources are located below the sediments, respectively. (e), (f) are the difference of relative errors of traveltime for VTI Model and ISO Model. The black line indicates the 0 contour line.

在图10中，对于沉积层内地震，ISO等效和VTI近似的误差随震中距均呈增大趋势.ISO等效的误差在0震中距时为0，即地震波垂向传播时ISO等效无误差；在震中距10 km以内，误差不超过10%；在震中距100 km时最大接近60%.VTI近似的误差在0震中距时为5%左右，震源越深误差越大；在震中距增大过程中，VTI近似的误差增速显著小于ISO等效，且快速趋于稳定；100 km震中距误差约45%.震源越深，两种近似方法的误差均越大，但VTI近似的精度优于ISO等效，如3 km震源可提高4%的精度，6 km震源可提高15%.对于沉积层下地震，ISO和VTI近似的总体误差均小于10%，表现了较好的精度；但VTI近似精度不如ISO等效，推测为THOMSEN弱各向异性近似产生的速度误差(李磊，2008).

在图11中，当震源位于沉积层内时，误差的极大值出现在右上角的大震中距、大震源深度区域；极小值存在一定的区别，即ISO模型出现在左侧0震中距处，震源深度对其基本无影响，而VTI模型出现在左下角的0震中距、小震源深度区域(图11(a，b)).当震源位于沉积层下时，两模型的误差呈现出更为复杂的变化规律.在小震中距(ISO模型的10 km，VTI模型的5 km)、小震源深度时，出现误差的极大值.ISO模型的误差极小值出现在0震中距处，而VTI模型的极小值出现在大震中距处(图11(c，d)).

3 分析与讨论

3.1 分析

通过模拟结果可以发现，震源与沉积层的位置关系对走时的影响极大.位于沉积层内的浅源地震，在震中距100 km范围内，进行各向同性等效的误差在给定震源深度情况下可达25%～60%.由此可见，在浅源地震时，对细密分层的沉积层进行各向同性等效，震中距的增大会带来巨大的误差.而在沉积盆地地区不论是固定台站还是流动台阵，其分布较为稀疏，很难真正接近震中位置，从而造成浅源地震的深度定位产生较大误差(王向腾等，2021).若考虑低频地震波在层状介质传播时产生的长波长效应，将细密分层的层状介质进行VTI近似后，其误差极大值为20%～45%，相较于ISO等效可降低5%～15%.位于沉积层下的中深源地震，在震中距100 km范围内，进行ISO等效的走时相对误差在5%以内，而进行VTI近似的误差相对较大，但仍不超过8%.因此，中深源地震时，相对于VTI近似而言各向同性等效是一种更简单且精度较好的等效方法.

为更清晰观察两种等效方法在不同震源深度和震中距情况下的优劣，将两者误差作差得到图11(e，f).当震源位于沉积层内，零值线(黑线)左侧为正值区，即该区域ISO模型误差更小，右侧为负值区，即VTI模型误差更小.零值线位于震中距5～10 km附近，随震源深度变化不大.当震源位于沉积层下，VTI模型与ISO模型误差的差值始终保持为正，即ISO模型的误差总是较小.

3.2 讨论

建模的尺度效应：本研究是根据天然地震和深部动力学研究的长波长特征，对塔中某井具有细密分层的层状介质进行了简单的各向同性等效和VTI厚层近似.图7所示层状模型实际上只是对一维测井数据进行分层的特例，在此基础上对其进行ISO等效和VTI近似.该建模方法综合了地质及测井数据，将明显的物性突变面作为地层分界面.但其等效速度、密度和各向异性参数与精确的测井数据建模得到的结果存在一定的差异(图9).根据测井数据得到的不同震源深度的等效速度均较图7层状模型更大，各向异性参数中ε和γ较图7层状模型更小，δ在中源地震时基本相同.由此可以发现，建模方法不同，其对应的等效介质参数会改变，即存在一定的尺度效应，从而影响地震波的传播.按照广义Backus平均等效理论(Kumar，2013)，该建模方法依赖于剖分尺度，领域已有足够多的研究讨论过类似问题(Hsu and Schoenberg，1988；Kerner，1992；Imhof，2003；Liner and Fei，2006；曹丹平，2015).因此，本文的数模结果只具有一般性的指导意义，走时误差具体数值会依赖模型的不同而存在差异.

波场的尺度效应：实际沉积层结构是极其复杂的，纵向上存在厚度、阻抗差异不同的变化，表现为随机互层介质的特点.对于这种介质的地震波传播研究，针对不同频率的子波，地震波的动力学和运动学特征也会呈现频率依赖性(White and Angona，1954；Levin，1979；Daley and Hron，1982；Helbig，1984；Melia and Carlson，1984；Lyakhovitskiy，1984；Roganov and Stovas，2012，2014；Stovas and Roganov, 2010; Stovas and Ursin, 2007; Stovas et al.，2013).如图12所示，本研究中，假设ISO等效和VTI近似分别满足左半支的短波长厚层和右半支长波长薄层的条件，对于复杂的、中间过渡带的干涉与散射问题(O′Doherty and Anstey，1971；Schoenberger and Levin，1974；Marion et al.，1994；Tang and Burns，1992)未予讨论.

图12 物理模拟和数值模拟对比(Marion et al.，1994)(a) 物理实验； (b) 数值模拟.Fig.12 The contrast of physical simulation and numerical simulation (Marion et al., 1994)(a) The physical experiments; (b) The numerical simulations.

弱各向异性假设：本研究对水平层状介质进行长波长各向异性等效时，假设各向异性强度较弱，满足Thomsen理论条件；但实际上，对于浅源地震，不同剖分建模方式存在各向异性强度超过10%，突破弱各向异性假设的问题；此时Thomsen理论给出的相速度误差问题已有讨论(李磊，2008)，本文不再赘述.

本文模拟分析的前提是震源与观测台站均位于盆地中，对于盆地台缘地震，盆地中观测，或盆地中地震，台缘接收的情况，盆地的沉积结构对走时误差的影响可能会弱化.

4 结论

上地壳浅部的沉积层由于其厚度相对较薄，其对地震波的影响在研究大尺度的壳幔结构时往往易被忽略.此外，在对浅源地震的震源深度进行定位时，不同的研究人员会给出相差极大的定位结果，这与地震台站在地表分布不均、在地下分布缺失是密不可分的.但是，地震定位时使用模型的精度与准确度也是至关重要的.虽然测井数据可以给出高精度的地层信息，但对于大尺度的壳幔结构而言，过于细密的分层是不必要的，且会带来巨大的计算量.因此，分析剖分尺度的影响，有利于在精确度和效率之间找到合适的平衡点.

通过分析塔里木盆地的精细水平层状沉积层模型，并进行各向同性等效和VTI近似两种简化，得到了对沉积层进行简化后带来的影响.一是震源所处的位置不同，即震源位于沉积内(浅源)和震源位于沉积层下(中深源)时，对沉积层进行简化后产生的走时误差呈现完全不同的变化规律.二是浅源地震进行简化后，在小震中距时走时误差较小，但在大震中距时误差很大，这会对壳幔结构研究和震源深度定位产生极大影响.三是深源地震进行简化后，产生的误差均较小，尤其是各向同性等效的走时误差可控制在5%以内，即深源地震时将沉积层简化为均一的各向同性层是合理的.

致谢感谢钮凤林教授对本文提出的修改意见，感谢两位审稿人提出的建设性意见和建议.感谢中石油为本文提供的塔里木测井曲线.