基于l1-l2范数的高分辨率时频分析方法及应用
邢文军,曹思远,陈思远,马敏瑶
中国石油大学(北京),北京 102249
0 引言
时频分析是地震资料处理中的重要分析方法,通过对地震数据进行时频分解,可获得每一时刻的频率成分;由于时频分析方法存在海森堡测不准原理的约束(Mallat,1999),即时间、频率的分辨率不能同时最优,使得带窗口类的时频分析方法应用受到了限制,包括短时傅里叶变换(Portnoff,1980;Margrave and Lamoureux,2001)、小波变换(Daubechies,1990;Chakraborty and Okaya,1995)、S变换(Stockwell et al., 1996; 高静怀等, 2003)等.在此基础上,受经验模态分解算法启发,基于带窗口类的时频分析可求取瞬时频率、通过能量挤压的方式提高频率分辨率,这一类算法统称同步挤压变换,根据窗口类时频分析方法的不同,具体可命名为同步挤压短时傅里叶变换(Oberlin et al., 2014; Wang et al., 2014; Mahdavi et al., 2021)、同步挤压小波变换(Chen et al., 2014; 潘晓等, 2020)等.
基于瞬时频率的思想,认为地震信号是由多个窄带信号(模态)相加而成,代表时频分析方法包括经验模态分解算法(Huang et al., 1998; Han and van der Baan, 2013)、集合经验模态分解(Wu and Huang, 2009; Wang et al., 2012)、变分模态分解(Torres et al., 2011;龙丹等,2020;邬蒙蒙等,2020)等,然后对分解后的固有模态分量进行Hilbert变换,最后将变换后的瞬时振幅、瞬时频率、瞬时相位等信息排列在时频平面上.一般来说,除含加性噪声的地震数据外,地震数据通常呈现不可分离的状态,即并不是由多个分量组成,且该类算法是数据驱动的自适应分解,稳定性较差.
同样基于瞬时频率的想法,稀疏反演时频分析方法认为在时频平面上,每一时刻振幅谱能量的极大值点是瞬时频率,然后通过稀疏约束反演的方法得到极大值点;代表方法包括以l1范数约束的短时傅里叶变换(Chen et al., 2020)、lp范数约束的短时傅里叶变换(Wang et al., 2020)等,这类算法的时频分辨率较高,目前这一类算法仍属于探索阶段(田琳和胡津健,2021;杨子鹏等,2021).
对于稀疏反演类时频分析方法,稀疏约束能力是决定时频分辨率的关键.已知稀疏能力最好的范数是l0范数,但是其求解困难(Natarajan,1995),在实际中一般使用l0范数的最优凸近似——l1范数代替求解(Chen et al.,1998),这将导致稀疏约束能力的下降,继而降低了时频分辨率;lp拟范数(Chartrand and Yin,2008)、l1-l2范数(Yin et al., 2015)、lp-l1范数(Zhao et al., 2020)等作为非凸范数同样具备稀疏约束能力,其中l1-l2范数的稀疏约束能力已被证明高于lp拟范数,已被广泛应用于地震数据处理中(Wang et al., 2018, 2019).
本研究提出基于l1-l2范数稀疏反演时频分析(L12-STFT)方法.L12-STFT通过短时傅里叶变换的逆变换构造目标方程,以l1-l2范数作为稀疏约束,通过交替方向乘子法(ADMM)进行求解,获得高分辨率的时频谱.模型部分证明了L12-STFT在时频分析分辨能力上的优越性,同时通过加噪数据的测试,证明L12-STFT具备一定抗噪性.实际数据部分基于L12-STFT进行谱分解,计算纵波频散属性,精确刻画储层.
1 理论
1.1 稀疏反演时频分析方法
本部分以短时傅里叶变换(STFT)为基础,推导基于稀疏反演的时频分析方法.
STFT首先将离散信号s∈N×1分解为N个长度为M(M为奇数,M yi=Gsi,(1) 其中G∈M×M表示对角线为高斯窗函数g∈M ×1的矩阵.si是以原信号s的第i个点为中心,信号两边各取(M-1)/2个数据作为子信号.同时为了减弱边缘效应,原始信号两端需补长度为(M-1)/2个零. 假设加窗后子信号yi的傅里叶变换为xi∈N×1,则xi和yi可表示为: yi≈SF-1xi,(2) 其中,S表示截断矩阵: S=[I|O],(3) I∈M×M为单位矩阵,O∈M×(N-M)为零矩阵.S矩阵的作用为截取F-1xi的前M个点,即去除无效值,F表示傅里叶变换矩阵,其形式为: (4) 令A=SF-1,即A表示部分傅里叶变换矩阵;则每一时刻的稀疏的反演方程为: (5) 式中,λ表示正则化算子,用以调整时频谱稀疏度,系数1/2作用在于简化求导过程.遍历信号si(i=1,2,…,N)即可得到信号s∈N×1的时频分析. 式(5)使用l0范数作为稀疏约束,其求解是NP-Hard问题,通常使用l1、lp等范数近似求解,本文使用l1-l2范数代替l0范数进行求解,图1为l2范数、l1范数、lp范数(p=0.65)和l1-l2范数的相平面图,显然,l1-l2与坐标轴近似度更高,更易获得稀疏解,相比于其他三种范数可以更好的近似l0范数. 基于上述讨论,修改式(5)为: (6) 其中,α为加权系数.式(6)表示l1-l2范数约束下的稀疏时频分析优化方程.正则化参数λ和α共同参与调节时频谱的稀疏度,两者越大,获得的时频谱稀疏度越高.反之两者越小,时频谱稀疏度越低,值得说明,当α减小为α=0时,l1-l2范数退化为l1范数. 式(6)可以使用凸差算法(DCA)和交替方向乘子法(ADMM)联合求解(Ma et al., 2017),这种求解方案在Wang等(2018)的研究中被得到了证实.由于凸差算法迭代速度较慢,本文建议只使用交替方向乘子法(ADMM)进行式(6)的求解(Lou and Yan, 2018),具体求解方式如下: 图1 稀疏约束的相平面图(a) l2范数; (b) l1范数; (c) lp范数(p=0.65); (d) l1-l2范数.Fig.1 Phase plane of sparse constraint(a) l2-norm; (b) l1-norm; (c) lp-norm (p=0.65); (d) l1-l2 norm. 分裂变量xi=zi,预定义迭代步长ρ,引入二次惩罚项,修改目标函数(6)为: (7) 式(7)需要两个变量交替进行求解,则xi更新为: (8) 式(8)只涉及l2范数可使用梯度下降法求解: (9) Z0更新为: (10) 需注意,当‖y‖∞=λ/ρ时,存在无穷多个解,但在实际处理中,因为数值的离散性,这种情况很难产生. 最后,对偶变量u使用对偶上升法进行更新,相应的更新迭代方程为: (11) 地震波在传播过程中的衰减往往伴随着频散,地层的速度与频率有关,则反射界面处的反射系数也与频率相关,即地震纵波频散属性可用作地层含气性的识别. 小波变换最早被应用于纵波频散的谱分解中,结合Smith和Gidlow方程有效描述了储层流体特征(Wilson et al., 2009; Wilson, 2010);近些年,随着高分辨率时频分析方法的不断革新,Wigner-Ville分布(Wigner, 1932)、匹配追踪(Mallat and Zhang, 1993)、VMD(Liu et al., 2016)、反演谱分解(黄广谭等, 2017)方法被用于纵波频散计算中,均不同程度提高了储层流体的识别精度,本文中所提出的L12-STFT也将被用于频散属性的计算. Smith和Gildlow近似方程为: (12) 式中,θi为入射角,VP和VS分别为纵波速度和横波速度,ΔVP和ΔVS分别为纵波速度变化量和横波速度变化量. (13) 式中,系数A(θi)和B(θi)与入射角和速度有关,可以通过射线追踪计算. 根据Chapman等(2006)的频散介质理论,可以得到具有频率依赖性的AVO近似方程,且对每个时刻t: (14) (15) 使用参数Ia和Ib表示反射率纵横波频散,即: (16) (17) 对于无频散情况,(14)式可修改为: (18) 地震数据S在时频域可写为反射系数和子波W(θi,f)的乘积,即: S(t,θi,f)=W(θi,f)[R(t,θi,f0)+α(t,θi,f)],(19) 其中,α(t,θi,f)=(f-f0)A(θi)Ia+(f-f0)B(θi)Ib,为反射系数的频散项,与反射系数纵横波频散项Ia和Ib相关.无反射系数频散时: S(t,θi,f0)=W(θi,f0)R(t,θi,f0). (20) 式(19)和式(20)说明,与时频域频谱白化类似,时频分析分辨率越高,相应的反射系数和地震数据的在时频域的特征越清晰,越有利于计算频散参数,将式(20)代入式(19)中,消除R(t,θi,f0),即: S(t,θi,f)W(θi,f0)-S(t,θi,f0)W(θi,f)= W(θi,f)W(θi,f0)α(t,θi,f),(21) 式中,α(t,θi,f)与纵横波频散项Ia和Ib相关,可通过求解式(21)获得纵横波频散参数. 根据上述纵波频散属性的推导,基于l1-l2范数的纵波频散参数计算流程如下: (1)对叠前地震数据进行几何扩散补偿、地表一致性振幅补偿、噪声衰减、动校正等处理,要求尽可能保幅处理.然后划分角道集、叠加,获得角道集叠加数据. (2)提取单道地震数据测试基于l1-l2范数的时频分析方法的参数,然后对地震数据进行分频,获得不同角度、频率的分频剖面S(t,θi,f)和S(t,θi,f0). (3)工区内含测井数据时,使用井数据和各角度道集提取角度子波,选取子波主频作为参考频率f0,计算子波振幅谱W(θi,f).工区内不含测井数据时可直接使用地震数据振幅谱的包络作为子波的振幅谱. (4)基于式(21)进行纵波频散属性计算,从而准确指示流体. 本部分测试基于l1-l2范数时频分析方法的聚焦性,并测试其抗噪能力. 模型一合成采样频率1024 Hz的调频信号(图2),共1024个采样点,调频信号s(t)的表达式为: (22) 图2 调频信号Fig.2 Original chirp signals 分别使用短时傅里叶变换(STFT)、同步挤压短时傅里叶变换(SST)、l1范数约束的反演时频分析(L1-STFT)和L12-STFT对上述调频信号进行时频分析,分析结果如图3所示,对比四种时频分析方法,L12-STFT的时频聚焦性最好(图3d),可定性的反映瞬时频率、瞬时振幅等信息;L1-STFT由于l1范数稀疏约束能力欠佳,时频谱的聚焦性(图3c)也弱于L12-STFT(图3d). 图3 调频信号的时频分析(a) STFT; (b) SST; (c) L1-STFT; (d) L12-STFT.Fig.3 Time-frequency spectrum of original chirp signals 模型二与模型一中的信号解析式相同,加噪后信噪比为6.488 dB,模型二信号如图4所示,其波形已被大量高斯随机噪声破坏;图5为四种方法对含噪调频信号的时频分析.综合四种方法分析,图5d中的L12-STFT有较高的抗噪性,依然可以良好的展示含噪调频信号的时频特征,主要原因是稀疏反演类时频分析方法使用l2范数作为拟合项,并使用稀疏范数作为正则化项,可压制高斯分布的随机噪声(Sun et al., 2021),且L12-STFT的稀疏约束能力较强.与之原理相近,由于l1范数稀疏能力较弱,L1-STFT在时频平面上出现很多噪声能量(图5c);如图5b所示,SST得到时频谱的原理是求取瞬时频率后的能量重分配,在瞬时频率准确求取的前提下,可有较好的抗噪性,但当噪声严重时,噪声被SST认为是有效能量,继而给予能量分配.故而相比于L12-STFT,SST抗噪性有限,在时频平面上也有噪声能量出现.图5a是STFT的时频谱,其不具备抗噪性,受噪声影响较严重. 图4 含噪调频信号Fig.4 Noisy chirp signals 图5 含噪调频信号的时频分析(a) STFT; (b) SST; (c) L1-STFT; (d) L12-STFT.Fig.5 Time-frequency spectrum of noisy chirp signals 模型三使用时间采样间隔为1 ms,主频50 Hz的Ricker合成地震记录测试时频分析的性能(图6),信号含随机噪声,信噪比为13.53 dB.对比方法包括基于lp范数的稀疏时频分析,即Lp-STFT(p=0.65),其中,短时傅里叶变换为窗长21ms的高斯窗,其余四种时频分析方法高斯窗的窗长为11 ms.测试结果如图7所示:STFT的时频分辨率仍然最低(图7a);地震子波的同步挤压变换(图7b)表现为“线”的形式,而反演类稀疏时频分析方法则表现为“抖动的能量团”(图7c—e),且能量团的时频聚焦性与正则化项的稀疏约束能力成正比,即L12-STFT时频聚焦性 >Lp-STFT>L1-STFT. 图6 反射系数(虚线)及合成地震记录(实线)Fig.6 Reflectivity (dotted line) and synthetic seismogram (solid line) 图7 合成地震记录的时频分析(a) STFT; (b) SST; (c) L1-STFT; (d) Lp-STFT(p=0.65); (e) L12-STFT.Fig.7 Time-frequency spectrum of synthetic seismogram 为了测试算法的抗噪性,使用时频聚焦性的表征参数Renyi熵测试不同信噪比(SNR)的算法性能,同一信噪比重复测试20次取平均值.Renyi值越小,表示时频聚焦性越好.测试结果如图8所示.测试结果表明,随信噪比降低,参与测试的时频分析方法的时频聚焦性均变差.但SST和稀疏反演类时频分析方法(L1-STFT、Lp-STFT、L12-STFT)的变化差异较小,且本文建议的L12-STFT的Renyi熵始终最小,这说明建议的方法在不同信噪比的数据测试中,均有较高的时频聚焦性. 图8 Renyi熵随信噪比的变化曲线Fig.8 Variation curves of Renyi entropy with SNR 本部分采用含气层的实际数据测试计算纵波频散属性,数据采样间隔为1 ms,目标储层约为2000 ms处,主要岩性为砂泥岩.图9为实际数据的近(图9a)、中(图9b)、远(图9c)三个角度叠加剖面,其中第293道存在横波测井数据,如图9所示,黑色曲线所示为纵横波速度比曲线. 图9 部分角道集叠加剖面Fig.9 Partial stacked sections of angle gather 首先对过井地震道进行时频分析测试(图10).图11为图10的时频谱,四种方法都可以在时频域上体现地震道的响应特征,如2000 ms的强振幅特征等,并且图11d所示的L12-STFT的时频聚焦性优于其余三种方法(图11a、b、c). 图10 过井地震道Fig.10 Cross-well seismic trace 图11 过井地震道的时频分析(a) STFT; (b) SST; (c) L1-STFT; (d) L12-STFT.Fig.11 Time-frequency spectrum of cross-well seismic trace 基于纵波速度(VP),横波速度(VS)和密度并利用Zoeppritz方程正演角道集,正演所使用的Ricker子波主频与地震数据主频相同(图12).通过合成的角道集可以测试该数据的频散属性响应特征.其中在1900~1950 ms和1950~2000 ms处呈现储层AVO响应(黑色虚线框),结合测井曲线分析,1900~1950 ms处为砂泥岩互层,泥岩含量偏高,储层质量差.1975~2000 ms处为砂岩气藏,上覆1975 ms为高GR的泥岩盖层,满足油气的储存条件;分别基于STFT、L1-STFT和L12-STFT对图12的角道集进行频散参数的计算,如图13所示,不同方法计算得到的频散曲线均能反应储层,且L12-STFT的分辨率较高(黑色虚线框). 图12 Zoeppritz方程正演的角道集Fig.12 Synthetic angle gather using Zoeppritz equation 对实际角道集叠加数据(图9)进行频散参数测试,三种方法的频散属性曲线上,在1975~2000 ms处的位置均产生异常,并且L1-STFT和建议的L12-STFT的分辨率最高,SST次之,STFT的频散属性分辨率最差(图14黑色虚线框).图15是这三种方法形成频散属性的剖面,基于L12-STFT计算的纵波频散属性分辨率最高,相比于L1-STFT,其频散属性剖面更整洁,能清晰描绘储层边界,刻画储层特征(图15黑色虚线框).需要指出,实际数据的频散属性与正演模拟的属性存在差异,原因在于实际数据中存在噪声、角道集划分准确度差、地震子波精度低等情况. 本研究提出一种基于l1-l2范数约束的时频分析方法,该方法受益于l1-l2范数强大的稀疏约束能力,联合短时傅里叶变换,可获得高分辨率的时频谱.纵波频散属性可以较好的指示流体,我们将基于l1-l2范数的高精度时频分析方法与频散属性相结合,提高了现有方法的纵波频散的分析精度.模型和实际数据均表明,本文提出的时频分析方法具有较高的时频分辨率,并且可以适用于地震数据分析. 图13 图11所示角道集计算的频散属性Fig.13 Calculated dispersion property of angle gather in Fig.11 图14 测井曲线和所计算的过井频散属性曲线Fig.14 Well-log curves and calculated dispersion attribute curves 图15 纵波频散属性剖面(a) STFT; (b) SST; (c) L1-STFT; (d) L12-STFT.Fig.15 P-wave dispersion attribute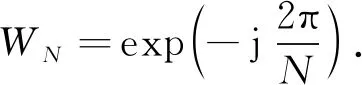
1.2 基于l1-l2范数的高分辨率时频分析及求解策略




1.3 地震频散属性
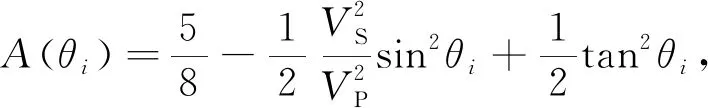


1.4 基于l1-l2范数的纵波频散参数计算流程
2 模型测试







3 实际数据测试




4 结论




