基于孪生网络的人工震源分布式光纤传感数据噪声压制

邵婕，王一博*，梁兴，薛清峰，梁恩茂，史树有

1 中国科学院地质与地球物理研究所, 北京 100029 2 中国科学院地球科学研究院，北京 100029 3 中国石油天然气股份有限公司浙江油田分公司，杭州 311100 4 北京辰安科技股份有限公司，北京 100094

0 引言

分布式光纤声波传感器(Distributed Fiber-optic Acoustic Sensing，DAS)是近年来新发展起来的，利用独特的分布式光纤探测技术对沿光纤传输路径上的空间分布和随时间变化的振动信息进行测量或监测的一种振动数据观测仪器，它基于光纤背向瑞利散射的原理，利用光纤作为传感器对地震信号进行采集.相比常规地震检波器，DAS具有低成本、高密度、高灵敏度、高效施工及可长期监测传输等优点，已在结构监测、渗漏探测、交通运输、安全系统、油气勘探及天然地震等领域引起了人们的广泛关注(李彦鹏等，2020；张丽娜等，2020；隋微波等，2021；Xu et al.，2021；周小慧等，2021).然而，这种新的地震数据采集技术也为DAS数据的后续应用带来了新的问题.以DAS在井中地震勘探中的应用为例，光纤电缆悬置在套管内，在这种情况下，光纤和地层的耦合效果差.套管内自由悬挂的电缆拍打和振铃会导致采集的数据中存在着相干耦合噪声，记录的地震数据显示出条纹或之字形的特征图案.此外，受随机噪声的影响，导致最终采集的套管井中悬置光缆DAS地震数据的信噪比很低，严重影响了DAS数据的后续应用.因此，研究针对DAS地震数据的噪声压制技术，提高数据信噪比，对提高后续的数据处理效果十分重要.

地震数据的噪声压制方法有很多，传统的去噪方法利用了有效信号和噪声在时空域或变换域内的差异，实现了增强有效信号及压制噪声的目的.时空域去噪方法包括：多项式拟合(Liu et al.，2011；李向云，2013)、中值滤波(王伟等，2012)及各向异性扩散滤波(张尔华等，2010)等.时空域去噪方法的去噪效果通常较为有限，尤其当数据的信噪比较低时，去噪效果较差.变换域内的去噪方法包括：基于小波变换(Mousavi et al.，2016)、S变换(李雪英和侯相辉，2011)、曲波变换(彭才等，2008)及seislet变换(Liu et al.，2015；张雅晨等，2019)等不同变换的去噪方法.这类方法是借助于各类数学变换方法将地震信号变换到变换域，然后利用有效信号和噪声在变换域内的差异，实现了二者的分离.另外，信号稀疏表示理论(Candèsand Demanet，2005)的发展促使了基于稀疏表示的地震噪声压制方法得到广泛应用(刘璐等，2021).它假设信号在某种变换的作用下是稀疏的，噪声是非稀疏的，从而有效地实现信噪分离.对于稀疏表示中的数学变换，除了采用传统的傅里叶变换、小波变换及曲波变换等，也可以通过字典学习方法(Zhu et al.，2015；Pilikos and Faul，2017；Shao et al.，2019)，直接从输入数据中学习数据本身的稀疏表达方式，从而适应地震数据的非稳态特征，提高去噪效果.Chen等(2019)研究了基于稀疏表示理论的DAS耦合噪声压制方法，根据有效信号和噪声在形态结构上的差异，分别采用小波变换和离散余弦变换表示有效信号和噪声，实现二者的分离.

传统的去噪方法虽然在一定程度上可以压制噪声，但大多数传统方法的参数选取都依赖于先验知识，这不仅影响着最终的去噪效果，当工区内的数据量很大时，也降低了地震数据的处理效率.近年来，人工智能方法在地震数据处理和解释中的应用逐渐广泛，如基于深度学习的地震数据初至拾取、插值、去噪、断层识别及储层预测等.相比于传统的去噪方法，基于深度学习的去噪方法通过各种不同的网络结构，对大量的数据进行训练，可以自动地深入挖掘出数据所包含的特征，从而有效地表示地震数据中的有效信号，压制噪声(Zhao et al.，2020).Liu等(2020)提出了基于三维卷积神经网络(3-D-DnCNN)的噪声压制方法，可以同时压制三维叠后地震数据中的随机噪声和弧状成像噪声.董新桐等(2021)提出了基于正演模型驱动的卷积神经网络去噪方法(FMA-CNN)，通过正演模拟构建了高真实性的无噪声地震数据集，利用该数据集以及实际DAS随机噪声数据集引导网络训练，从而有效地实现DAS地震数据的随机噪声压制.上述方法在网络训练的过程中，需要提供大量的无噪声数据作为标签数据，然后将其与对应的含噪声数据进行成组标记，人工标记工作量巨大.对于实际地震数据而言，无噪声数据通常很难直接获取.对此，可以将传统去噪方法处理后的结果作为标签数据，但这会导致标签数据不准确，从而影响了训练网络的去噪效果(Li et al.，2021；陈文超等，2021；Liu et al.，2022).另外，也可以采用正演模拟的方式产生无噪声数据，但这会导致模拟的数据难以表征复杂实际数据的特征，从而影响了训练网络的泛化能力.

本文将孪生网络方法应用于人工震源分布式光纤声波传感数据中的随机噪声压制.基于孪生网络的基本思想，该方法采用了U-Net网络建立深度学习框架，包括输入层、编码器、解码器和输出层四部分.参与训练的输入数据只需要含噪声的原始数据，不再需要利用无噪声数据对原始的含噪声数据进行标记.训练后的网络可直接应用于含噪声数据的去噪处理，为实际地震数据去噪处理带来了便利.最终，采用合成数据和实际资料验证了本文所研究方法的有效性.

1 方法原理

实际采集的地震数据中通常包含了部分噪声，假设y为含噪声的地震数据，则它可以表示为

y=x+n,

(1)

其中，x为无噪声的有效信号，n为噪声.传统的监督学习去噪网络需要含噪声数据y和无噪声数据x作为标签数据，然后将成对的输入数据(y,x)输入网络f进行训练，获得将含噪声数据y映射为无噪声有效信号x的最佳网络参数θ，从而实现去噪目的.监督学习网络训练的目标函数为

(2)

在实际应用中，无噪声数据通常很难获得，尤其是对于分布式光纤地震数据而言，高信噪比数据的数据量往往很少.通过正演模拟方式获得的地震有效信号难以全面地表征实际有效信号的特征，从而影响最终训练网络的泛化能力.此外，大量的正演模拟也给实际应用带来了极大的不便.

如果能只使用含噪声数据进行网络训练，则会有效地克服传统监督学习去噪网络在实际地震数据去噪应用中的瓶颈.为此，假设噪声的均值为0，则给定自监督网络训练的目标函数如下(Xie et al.，2020)：

-f(yJc;θ)J‖2/|J|]1/2,

(3)

其中，E表示对数据取均值，m表示输入数据y的空间维度，J可作为一个mask算子，通过它可以获得数据的某一个子集(如图1所示)，|J1|+…+|Jk|=m，JC表示J在m中的补集，f(·)J表示f(·)在J上的取值，yJc表示y在JC上的取值.

从公式(3)的目标函数可以看出，该网络在训练时需要含噪声数据y和由数据y经mask算子作用后的yJc(如图1所示)，无需再使用无噪声数据.因此，它属于自监督网络.为此，基于孪生网络的思想，采用U-Net网络建立如图1所示的深度学习去噪网络.该网络由输入层、编码器、解码器和输出层4个部分组成.原始的输入数据首先经过两个卷积层，每一个卷积层包含了4个滤波器，步长为1.编码器由4组下采样层和卷积层构成.编码器中所有的下采样层都具有反假频特征(Zhang，2019)，以避免下采样过程中的假频影响.每个下采样层后都有两个卷积层，各组卷积层中的滤波器数量逐渐加倍，即分别为8、16、32、64.解码器由4组上采样层、拼接层和卷积层构成.在解码器中，每一组都包含一个上采样层和拼接层及两个卷积层，各组卷积层中的滤波器数量逐渐减少，即分别为32、16、8、4.最终的输出层是由滤波器和线性激活函数构成的卷积层.建立的网络中所有卷积层的卷积核大小均为3×5.

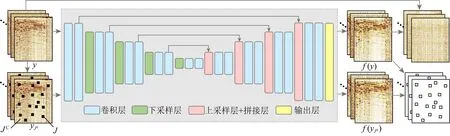
图1 去噪网络结构示意图Fig.1 Structure of the denoising network

2 模型算例

为了验证本文提出的基于孪生网络的DAS数据去噪方法的有效性，首先采用合成数据进行测试.通过正演模拟获得了原始无噪声的人工震源井中分布式光纤数据，每炮数据共有50道，每道数据的时间采样点数为2048，数据中包含了P波和S波，且S波的能量明显强于P波.在原始无噪声数据中加入信噪比值分布在-20～10 dB范围内的随机噪声，最终获得用于网络训练的含噪声数据共4288炮.图2展示了训练集中的部分地震数据，不同炮数据间的地震波波形、振幅、相位、同相轴的斜率及信噪比等特征各不相同.选取其中80%的数据(共3424炮)作为训练集，用于进行去噪网络训练，获得实现最佳去噪效果的各网络参数值.为了分析和验证训练网络的去噪效果，选取其中20%的数据(共864炮)作为验证集.在合成数据的网络训练时，设置批大小(batch size)为32，时期次数(epoch)为5000，图3为合成数据进行去噪网络训练时损失函数值随时期次数的变化曲线.

图3 合成数据去噪网络训练的收敛曲线Fig.3 Convergence curve of denoising network training for synthetic data

在训练获得去噪网络的最优参数后，选取如图4所示的数据测试训练网络的去噪效果.该数据的特征与参与网络训练的数据特征相似，即数据中包含了P波(黑色箭头所示)和S波(蓝色箭头所示)，且S波的能量明显强于P波.不同之处在于地震波波形、振幅、相位及同相轴的斜率特征.在原始数据中分别加入信噪比为9.03 dB、0 dB和-6.99 dB的随机噪声，然后将训练的网络参数直接应用于不同信噪比的含噪数据，获得的去噪结果及去除的噪声分别如图5、6、7所示.

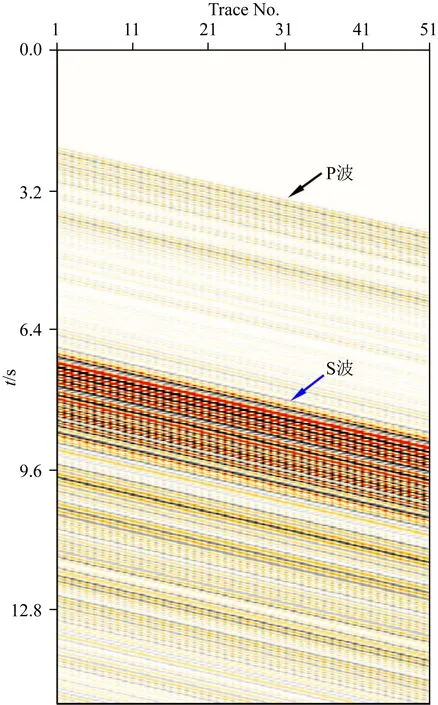
图4 无噪声的井中分布式光纤合成数据Fig.4 Synthetic downhole DAS data without noise

当含噪声数据的信噪比较高时(SNR=9.03 dB)，仍可以识别出含噪数据中的弱能量P波，如图5a所示.在这种情况下，训练的网络可以完全地压制原始数据中的噪声，去噪的结果(如图5b所示)与真实数据几乎相同，去噪后数据的信噪比为20.37 dB.但去除的噪声中残留了部分S波能量，如图5c所示.这主要是由于训练网络无法有效地恢复地震有效信号的振幅导致的.从网络训练的目标函数可以看出，该网络训练的主要目标在于去除噪声对有效信号的影响，训练的网络无法可靠地估计有效信号的真实振幅值.当信噪比值为中等(SNR=0 dB)时，加入噪声后的弱能量P波完全淹没于噪声中，难以有效地识别出来，强能量的S波初至仍可识别，但后续的弱能量S波也几乎淹没于噪声中，如图6a所示.在这种情况下，噪声仍可以被有效地压制，弱能量的P波和后续S波都得到了较好的恢复，去噪后数据的信噪比为12.73 dB，如图6b所示，去除的噪声如图6c所示.当信噪比较低(SNR=-6.99 dB)时，加入噪声后的弱能量P波和后续的弱能量S波都已完全淹没于强噪声中，只有强能量的S波初至仍可识别.在这种情况下，噪声仍得到了有效压制，弱能量的P波和后续S波得到了部分恢复，如图7所示，去噪后数据的信噪比为6.64 dB.

为了进一步定量地分析本文提出方法的去噪效果，我们对图4中的数据加入了信噪比值分布在-20～40 dB范围内的随机噪声，对加入噪声后的各数据分别进行处理，并按照公式(4)计算了每一个信噪比情况下所有道去噪后数据和真实无噪声数据间归一化的均方误差(MSE)，结果如图8所示，图中的误差棒由公式(5)给出，是不同道去噪后数据和真实无噪声数据之间均方误差的标准差(STD).

(4)

(5)

(6)

从图8可以看出，随着SNR的增加，由公式(4)计算的MSE值不断减小.因此，随着数据中噪声的不断减少，去噪结果和真实数据之间的差异不断减小，去噪效果不断变好.当信噪比达到某一程度时，二者的差异趋于达到稳定值.另外，随着SNR的增加，计算结果的标准差整体也呈现出减小趋势，但部分数值会有起伏变化，如7 dB处的误差棒较周围其他值明显变长.这可能是由于去噪方法无法有效地恢复地震有效信号的振幅导致的.

3 实际资料

选用某地区的人工震源井中分布式光纤数据对本文所提出方法进行进一步测试，实际数据采集的观测系统示意图如图9所示，光纤布设在套管外.该数据共80炮，每炮数据包含712道，每道数据的时间采样点数为2048.由于实际数据的数据量较少，因此，我们将上述合成数据的训练结果作为预训练模型，在此基础上，继续进行实际资料的网络训练.这就要求合成数据应该具有与实际数据相类似的特征，否则无法使用.如果实际数据量足够多，则无需选用合成数据的训练结果作为预训练模型.在训练过程中，选取65炮数据作为训练集，剩余的15炮数据作为验证集，设置批大小为32，时期次数为50.图10为实际资料进行网络训练时损失函数值随时期次数的变化曲线，可以看到，由于选用合成数据的训练结果作为预训练模型，实际数据的训练网络能够很快地达到收敛.从实际资料中分别选出高信噪比、中等信噪比和低信噪比三种不同情况下的去噪结果进行分析，得到结果分别如图11、12、13所示.从去噪结果中可以看出，训练的网络都能较好地压制剖面中的噪声，去噪后的同相轴变得更加连续.从去噪后的残差剖面中可以看出，高信噪比数据的残差剖面中包含了部分有效信号的能量，这同样是由于训练网络无法有效地恢复地震有效信号的振幅导致的.

图8 不同信噪比时合成DAS数据的去噪效果Fig.8 The denoising result of synthetic DAS data with different SNRs

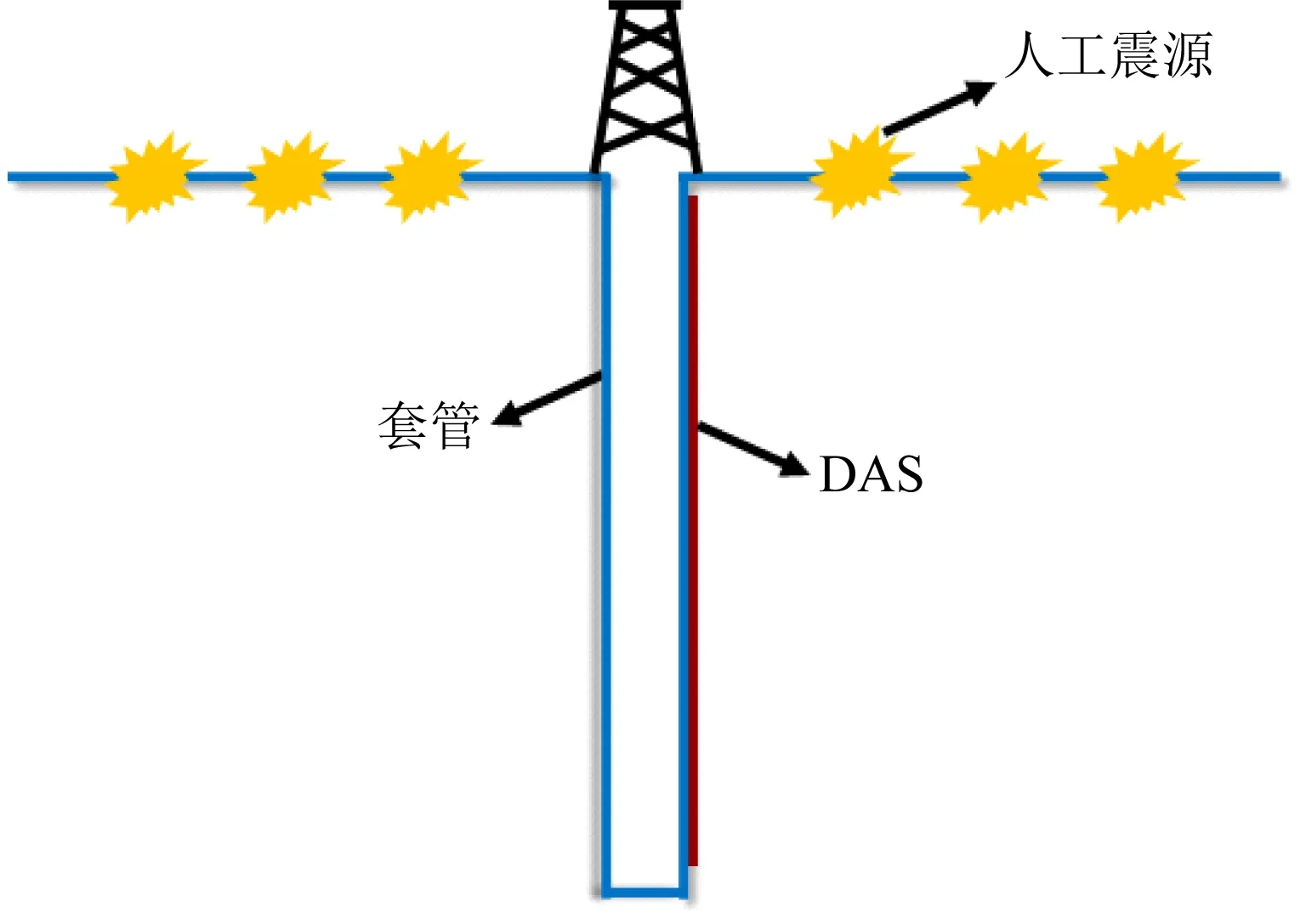
图9 井中分布式光纤数据采集观测系统示意图Fig.9 Diagram of borehole DAS seismic data acquisition geometry

图10 实际资料进行去噪训练的收敛曲线Fig.10 Convergence curve of denoising training for field data

图11 高信噪比实际资料去噪(a) 含噪声数据； (b) 去噪结果； (c) 去除的噪声.Fig.11 Denoised result of field data with high SNR(a) Noisy data; (b) Denoised data; (c) The removed noise.

图12 中等信噪比实际资料去噪(a) 含噪声数据； (b) 去噪结果； (c) 去除的噪声.Fig.12 Denoised result of field data with medium SNR(a) Noisy data; (b) Denoised data; (c) The removed noise.

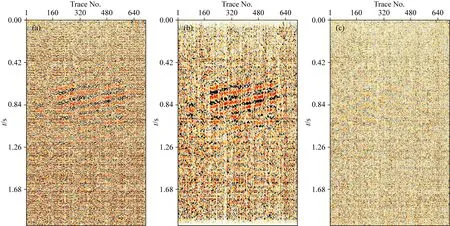
图13 低信噪比实际资料去噪(a) 含噪声数据； (b) 去噪结果； (c) 去除的噪声.Fig.13 Denoised result of field data with low SNR(a) Noisy data; (b) Denoised data; (c) The removed noise.

4 结论

本文将孪生网络应用于人工震源分布式光纤传感数据的去噪处理.合成数据和实际资料的处理结果表明，本文方法可以有效地压制人工震源分布式光纤地震数据中的随机噪声.与传统的监督学习去噪方法不同，本文方法属于自监督学习方法，在网络训练过程中，不需要使用去噪后的数据对原始含噪声数据进行人工标记，这非常有利于实际应用，可以显著地提高实际地震数据去噪处理效率.本文方法的不足与限制在于它无法有效地恢复地震有效信号的振幅，导致去除的噪声剖面中会残留部分有效信号的能量.因此，后续仍需进一步研究并改进本文方法，以提高其对有效信号振幅的恢复和保护作用.

致谢感谢审稿专家对文章提出的宝贵意见，感谢编辑对文章的修改完善.