基于一维卷积神经网络的高分辨率Radon变换反演方法研究

薛亚茹，郭蒙军*，冯璐瑜，马继涛，陈小宏

1 中国石油大学(北京)信息科学与工程学院，北京 102249 2 中国石油大学(北京)地球物理学院，北京 102249

0 引言

地震勘探包括地震数据采集、处理和解释三个主要环节，其中数据处理通过各种数学、物理等方法处理采集到的地震数据，为之后的地震资料解释提供高质量数据支撑(杨子鹏等，2021；郑迎冬等，2021).Radon变换是地震数据常用处理方法之一，最早由Claerbout和Johnson(1971)引入地震勘探领域，之后被广泛应用于多次波压制(Zhang and Wang,2006;Kazemi and Sacchi,2021)、缺失地震道重建(王维红等，2007；唐欢欢等，2020)和波场分离(曾有良等，2007; 朱翔宇等，2018)等工作中.

Radon变换的基本原理是将不同曲率的同相轴映射到Radon域参数，以实现同相轴特征识别.但由于地震数据采集系统是有限的离散空间，导致同一同相轴会映射Radon域的多个参数，引起分辨率降低；同时由于Radon变换是非正交变换，导致其无法保留数据真振幅.针对上述问题，学者们展开了Radon变换反演方法研究.Thorson 和 Claerbout(1985)提出基于最大后验概率(Maximum A Posteriori, MAP)的随机反演思想，改善了Radon变换分辨率，该方法在时域实现Radon反演，反演矩阵维度大，计算量大.对于动校正后的地震剖面，Hampson(1986)提出了频率域抛物Radon变换，不同频率反演解耦，大大提高了计算效率，但该方法采用最小二乘反演，得到的Radon变换参数光滑，分辨率较低.为提高Radon变换分辨率，Sacchi和Ulrych(1995)提出基于贝叶斯原理的反演理论，将模型的先验信息作为正则化约束稀疏反演，得到了频域高分辨率Radon变换.在此基础上，Sacchi和Porsani(1999)利用共轭梯度和循环矩阵提高了高分辨率Radon变换处理大型数据时的计算速度.为进一步提高计算效率，有学者提出频率约束的思想，即选择一个主要频率分量，以此频率分量来约束其他所有频率，避免因迭代过程中矩阵求逆导致计算量大的问题(Herrmann et al.,2000;Chen and Lu,2011；刘仕友等，2019).

频率域Radon反演方法虽然有效提高了计算效率，但对时域没有稀疏约束.Cary(1998)指出时域算法可以实现时间和Radon参数两者的稀疏性，分辨率进一步提升，但是计算速度相比于频域算法较慢；之后Trad等(2003)结合了Radon变换时域的稀疏性以及频域的计算高效性，实现了混合域Radon变换；熊登等(2009)为频域抛物Radon变换引入时变稀疏权，在混合域实现了高分辨率抛物Radon变换，并用于多次波衰减；随后Lu(2013)在混合域求解过程中引入了迭代收缩算法，进一步提高了混合域Radon变换的计算效率；考虑地震数据受非高斯噪声分布影响，Wang等(2019)提出时域双L1范数稀疏约束的鲁棒时不变Radon变换，并引入交替分割Bregman算法来提高Radon模型计算效率.对于双曲Radon变换时域求解效率低下的问题，Hu等(2013)通过构造双曲Radon算子的低秩近似和蝴蝶结构，提出一种快速求解双曲Radon变换的蝴蝶算法，实现了单个积分算子的快速求解；面对速度各向异性发育介质及长偏移距情况下的地震数据，巩向博等(2014)提出各向异性Radon变换，改善了复杂地质条件下Radon域能量不收敛的问题，并利用最优相似系数加权Gauss-Seidel迭代算法，具有较高的时域计算效率；Gholami和Farshad(2019)通过延时间轴插值拉伸数据，并用基于快速傅里叶变换的chrip-z变换快速计算新坐标系下的求和路径，得到一种快速计算双曲Radon变换及其稀疏计算的方法.

上述学者从不同角度解决Radon变换面临的计算效率和反演分辨率问题.由于Radon变换空间是不同曲率的时距曲线，其分辨率越高，Radon反演基函数相关性越强，反演矩阵病态性越强，目前的线性反演方法难度越大，因此有待于提出新的反演思路改进Radon变换.

近几年，人工智能和深度学习在计算机视觉和图像领域快速发展，对于反问题求解，Gregor和LeCun(2010)在稀疏编码背景下提出学习型的迭代软阈值算法，通过训练具有特定结构和固定深度的非线性前馈预测器，学习传统迭代软阈值算法的两个矩阵，以此得到稀疏编码的最佳近似，提高了稀疏编码的效率，此后，有关逆问题求解的深度学习方法不断涌现.Yang等(2016)将传统的交替方向乘子法与神经网络相结合，用来重建磁共振图像，网络以端到端的方式进行训练，网络架构结合了传统的交替方向乘子算法，增强了网络的可解释性；除此之外，Borgerding等(2017)通过展开传统的近似消息传递算法，提出了基于近似消息传递算法的用于求解线性逆问题的深度神经网络.为解释深度学习框架适用于图像特定反问题求解的合理性，Ye等(2018)提出一种通用的求解反问题的深度卷积框架神经网络(Deep Convolutional Framelets Neural Network, DCFNN)，表明深度神经网络中的残差块、级联ReLU函数和冗余滤波通道有助于实现逆问题求解，揭示了现有求解逆问题深度学习网络架构的局限性.对于欠采样磁共振图像重建这一不适定线性反演问题，Mardani等(2019)提出一种基于生成对抗网络(Generative Adversarial Network, GAN)的压缩感知方法，其中生成器为一个带有跳跃连接的深度残差网络，用来消除混叠伪影，判别器为一个多层卷积神经网络，用来评判映射后的图像质量.有别于展开迭代优化算法的神经网络，Gilton等(2019)通过截断Neumann级数，提出一个求解逆问题的端到端，数据驱动的Neumann网络，在标准数据集上的效果要优于展开的迭代方法.Ongie等(2020)总结了近些年深度学习在求解图像逆问题领域的应用，并根据前向模型是否已知以及网络是否为监督或无监督学习对其进行了分类.

深度学习的发展也促进了Radon变换反演问题的研究.Kaur等(2020a)通过建立CycleGAN网络来近似逆Hessian矩阵，得到与传统迭代反演类似的效果，且计算量相较于传统算法有所下降；之后，Kaur等(2020b)将CycleGAN网络学习逆Hessian矩阵的方法用于求解双曲Radon变换，在降低计算量的同时达到了与传统最小二乘法相同的结果.上述GAN网络需要生成器和判别器协同完成逆Hessian矩阵的学习，网络结构较复杂.本文结合Radon变换的卷积模型，通过建立简单的一维卷积网络模型，借助于卷积神经网络的非线性表征能力，实现高分辨率Radon变换反演；具体分析串、并联两种模型神经网络的工作机理，与传统高分辨率Radon变换反演方法进行对比，验证本文提出的卷积神经网络实现高分辨率Radon变换的可行性及有效性.

1 Radon变换基本原理

地震数据处理中常用的Radon变换有线性Radon变换、抛物Radon变换和双曲Radon变换，其中线性Radon变换和抛物Radon变换具有时不变性，可通过Fourier变换从时间-空间域变换到频率-空间域，实现不同频率数据解耦，降低反演矩阵维度.以抛物Radon变换为例，地震数据可以表示为沿不同曲率抛物路径的同相轴叠加，即：

(1)

其中t为时间，τ为时空域双重走时截距，q为曲率参数，h为偏移距，Nq为Radon域中曲率参数个数.

将式(1)变换到频域，有：

(2)

式中e-iω qjh2表示频率为ω，曲率为qj的同相轴，其相位随偏移距h的增加而增加.由于抛物Radon变换可以用上述简单的相移参数表示同相轴的随偏移距的展布，而且不同频率之间相互独立，因此抛物Radon变换可以分频处理.对某一频率分量，将上述相移算子用矩阵表示：

(3)

式中Nh为道数，每一列表示了不同曲率参数的Radon变换基函数.Radon变换表示为矩阵形式：

d=Lm,

(4)

其中d表示某一频率分量的地震向量，m为其对应频率分量的Radon参数向量.对式(4)转置运算，可得到Radon共轭解：

mH=LHd.

(5)

将式(4)代入式(5)，可得到共轭解与真实Radon参数之间的关系：

mH=LHd=LHLm.

(6)

由于Radon变换算子L是非正交的，所以LHL不是单位矩阵，也就表明Radon共轭解mH并不是真实的Radon参数.又因Radon算子L被限制在有限偏移距范围内，使得同相轴无法聚焦到一个理想的Radon曲率参数，从而产生扩散，且采集范围越小，扩散越严重.

为克服Radon变换的非正交性，通常采用最小二乘法降低重构数据与真实数据之间的误差，定义优化函数为：

由式(7)可得到Radon变换最小二乘解为：

m=(LHL)-1LHd.

(8)

上述Hessian矩阵求逆不稳定，且分辨率低.Sacchi和Ulrych(1995)提出基于Bayes理论的随机反演方法.该方法将模型的先验信息引入反演过程，形成正则化目标函数：

(9)

其中Wm是对参数的正则化约束，μ为阻尼因子.当Wm为单位矩阵时，正则项与先验参数没有关系，仅引入阻尼因子，实现对参数的光滑约束，分辨率不高；当假设Radon参数服从Cauchy分布时，Wm为Radon参数的协方差对角矩阵，即Wii=1/(|mi|2+b2)；当采用L1范数正则化约束，Wii=1/(|mi|+b2)，其中b都是一个较小的数，避免分母为零.

上述正则化方法是目前Radon变换反演的主要方法，通常采用迭代求解方法，例如迭代加权最小二乘法(Iterative Reweighted Least Square, IRLS)，迭代收缩阈值法(Iterative Shrinkage Threshold Algorithm, ISTA)等，在这些方法中都无法避免Hessian矩阵求逆带来计算量大的问题；同时对于迭代优化方法，在使用过程中权重系数μ的选取，迭代次数等超参数都需要进行调整优化，影响数据处理质量.

2 基于褶积模型的Radon变换反演

2.1 Radon变换的褶积模型

Radon变换反演通常采用数据d与参数m之间的反演映射关系，算子L是非正交矩阵，且不同曲率参数的Radon变换基函数相关性较大，带来矩阵求逆的不稳定性、矩阵求逆计算量大等问题.观察式(6)，它建立了Radon共轭解与真实解之间的映射关系，其中映射算子是Radon算子的自相关矩阵，构成了一个共轭对称的Hessian矩阵.定义该矩阵为Φ=LHL，具体形式为：

(10)

(11)

其中*表示褶积运算，褶积核函数由Φ矩阵的第一列和第一行构成，mqi为不同曲率对应的Radon参数.图1a所示为30 Hz的褶积核，该褶积核函数对真实Radon参数的褶积形成了一个低通滤波作用，因此可被描述为一个模糊褶积算子(Hu et al., 2001).

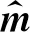
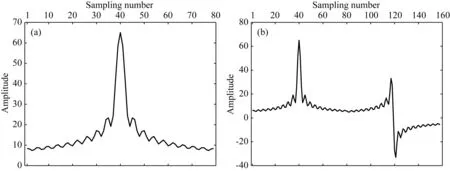
图1 褶积核数据(a) 幅度； (b) 实部和虚部串接.Fig.1 Convoluted kernel data(a) Amplitude； (b) Concatenation of real and imaginary part.

神经网络通常处理实数数据，对于复数数据，本文采用将复数实部与虚部串联构成实数序列，图1b为褶积核的实部和虚部的串接，构成了一个更为复杂的褶积核函数.

2.2 基于反褶积原理的串联反演模型

根据式(11)建立的褶积模型，可以设计反褶积滤波器，实现高分辨率Radon变换反演.基本原理如图2所示，与褶积核形成串联模型关系.

图2 反褶积滤波器Fig.2 Deconvolution filter

由图2可以得到串联神经网络模型F1与褶积核函数关系为：

F1=CNN(Φ)=Φ-1，(12)

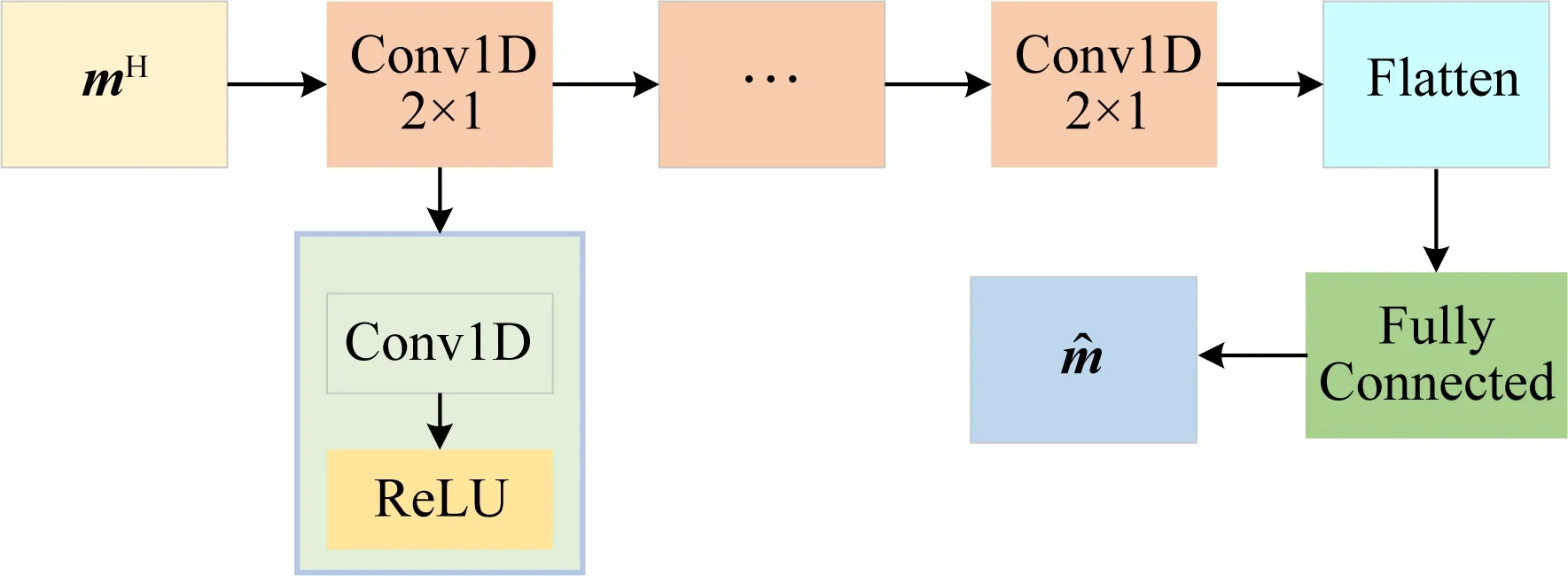
图3 串联型一维卷积网络Fig.3 Serial 1-D CNN

式中CNN为建立的串联型一维卷积网络，用来学习Radon变换反褶积算子，实现低分辨率解到高分辨率解的映射.本文串联型一维卷积网络结构如图3所示，包含卷积层、展平层和全连接层，其中每个卷积层都包含一个一维卷积过程和一个ReLU激活函数，其中一维卷积用来学习数据特征，ReLU激活函数为网络提供非线性变换，卷积层的个数可根据数据复杂度进行调整；展平层用来将多维数据转化为一维数据，以进行后续处理；全连接层包含一个线性激活函数，用来连接送入网络的数据标签值和卷积网络学习到的数据特征.

2.3 基于残差学习的并联反演模型

提高分辨率亦可以通过预测低分辨率解与真实解之间的差异，去除Radon卷积核的模糊作用(Ongie et al.,2020).该方法通过学习低分辨率共轭解与真实解之间的残差，实现分辨率提高.通常采用跳跃连接网络实现差异预测，例如残差网络，多级跳跃连接的U-net网络等，这些网络在提高图像辨率、数据预测应用中表现良好.为了方便与反褶积模型工作原理比对，本文设计如图4所示的简单一级跳跃残差网络结构，该网络与低分辨率数据形成并联关系，与串联模型呼应称之为并联反演模型.

图4 并联反褶积模型Fig.4 Parallel deconvolution model

由图4可得到并联反演神经网络模型F2与Radon褶积核函数关系为：

(F2+I)Φ=I，(13)

即：

F2=CNN(Φ)=Φ-1-I，(14)

由此可以看到并联网络表示的是Hessian逆矩阵的变化部分.

上述并联型网络模型输出低分辨率数据与神经网络输出之和：

=BN(mH+CNN(mH))，(15)

串联模型中网络学习的是Radon变换反褶积算子，而并联模型中网络学习的为高分辨率解与低分辨率解之间的残差.本文从两个不同角度设计网络，以寻求较好的网络实现高分辨率Radon变换，并解释神经网络反演的工作机理.

2.4 频率约束

由于褶积算子Φ与频率有关，而不同频率对应不同的Radon算子，使得卷积网络实现的是单一频率低分辨率解到真实解的映射.若要实现所有频率的映射，就需要训练不同频率的数据，得到对应频率的网络，工作量较大.为此，本文引入频率约束的思想(Chen and Lu,2011)，将网络训练得到的单个频率的结果约束其他所有频率的反演，这里将网络结果作为Radon反演先验信息嵌入迭代加权最小二乘法，以此来减少工作量，提高计算效率.最终基于网络的高分辨率Radon变换求解公式为：

(16)

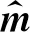
3 数据实验

为验证本文卷积网络的可行性和有效性，本文将建立的一维卷积网络用于处理模拟数据和实际地震数据多次波分离实验，并与传统的迭代加权最小二乘法求解的高分辨率Radon变换进行比较.本文中网络训练环境为Intel Core i5-8300H CPU，主频2.30 GHz，内存16 GB，GPU为NVIDIA GeForce GTX 1050 with Max-Q Design.

3.1 数据集准备

假设图5a是模拟的待分离一次波和多次波简单合成记录，图5b是其Radon参数.为反演Radon参数，提高网络性能，需要模拟相同分布的大量训练数据.在真实Radon参数周围随机选择一些Radon参数，由此生成一组与所求Radon参数分布类似的数据，变换到频域后选择主频对应的Radon参数作为标签数据.之后利用式(6)得到其对应的低分辨率共轭解作为输入数据，与标签数据共同构成数据集，以这种方式共生成11000个数据样本，其中10000个样本作为训练集，剩余1000个样本作为测试集.串联网络模型和并联网络模型数据集相同，即以低分辨率共轭解作为输入数据，其对应的实际解作为标签数据.

真实Radon参数和其对应的低分辨率解为复数，而网络训练数据为实数.为此，本文将复数的实部和虚部串联转化为实数，一同送入网络.

3.2 数据实验

图5a为主频30 Hz的Ricker子波合成的CMP地震道集，共50道，采样点为500个，采样间隔2 ms，它包含三个一次波同相轴，零偏移时间分别为0.2 s、0.5 s和0.8 s，以及四个多次波同相轴，零偏移时间分别为0.1 s、0.3 s、0.5 s和0.7 s，图5b为其对应的Radon域参数.本文使用Keras建立串联型和并联型一维卷积网络，并基于Tensorflow进行测试训练，两个网络都使用Adam算法来优化学习目标，采用均方误差损失函数，设置初始学习率为0.001，epoch为80次，Batch size为20.

图5 模拟地震数据(a) 模拟地震数据； (b) 模拟Radon参数.Fig.5 The synthetic seismic data(a) The synthetic seismic data； (b) The synthetic Radon model.

本文采用信噪比(Signal-to-Noise Ratio, SNR)衡量Radon变换地震数据的恢复效果以及对多次波的压制效果，信噪比定义为：

(17)

式中dr指原始地震数据或者原始一次波数据，dm指各种方法恢复的地震数据或恢复的一次波数据.

3.2.1 卷积层属性对网络性能的影响

为了得到较好的反演效果，以原始数据重构和一次波分离信噪比作为参考指标，测试了不同卷积层属性对结果的影响.

表1和表2分别为卷积层属性对串联型网络和并联型网络的影响.对于串联型卷积网络，本文采用的卷积核大小为3×1，步长为1，卷积层后为ReLU激活函数.从表1可以看到，如果每个卷积层都包含16个卷积核，则当网络深度为5即网络有四个卷积层时网络性能最佳，此时对多次波的压制效果最好，地震数据恢复的信噪比与其他网络层数恢复的信噪比接近；对于相同的网络深度，当采用混合卷积核，即表1中卷积层个数为5，卷积核个数依次为8、16、32、64、128时，网络性能要弱于每个卷积层中卷积核个数都为16时的网络性能，且网络训练耗时更长.为此本文搭建的串联型网络结构包含5个卷积层，每个卷积层中包含16个卷积核，卷积核大小为3×1，步长为1，激活函数为ReLU函数.

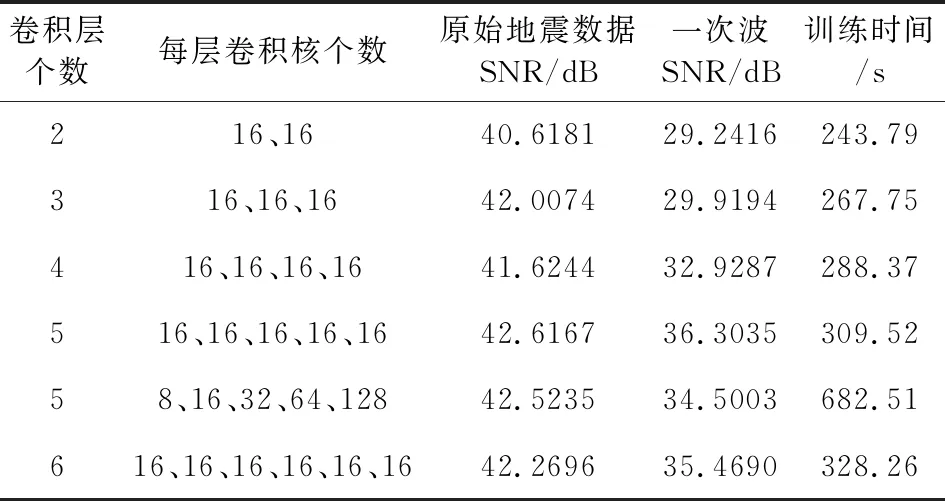
表1 卷积层属性对串联型网络性能的影响Table 1 Influence of convolution layer on serial network

并联型卷积网络测试结果如表2中所示.当每个卷积层都包含16个卷积核，且网络含有5个卷积层时，网络对多次波压制效果最好，当网络采用混合卷积核，即表2中网络卷积层个数为5，卷积核个数依次为8、16、32、64、128时，与全为16个卷积核的网络相比，两者都能有效压制多次波，但其网络训练时间大幅增加.综合考虑对多次波的压制效果以及网络效率，本文搭建的并联型网络同样采用5个卷积层，每个卷积层包含16个卷积核，卷积核大小为3×1，步长为1，卷积层之后为ReLU激活函数.

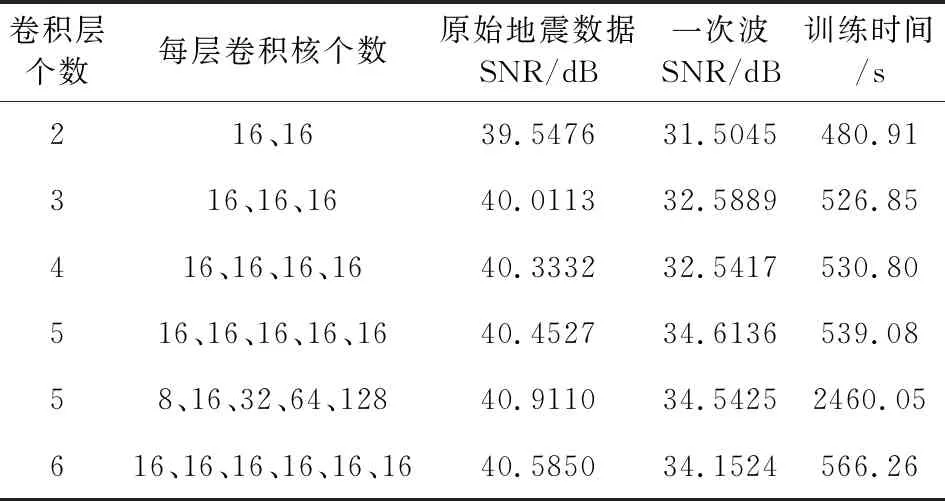
表2 卷积层属性对并联型网络性能的影响Table 2 Influence of convolution layer on parallel network

3.2.2 模拟数据反演结果

首先，对频率30 Hz的Radon参数进行反演，串联型一维卷积网络、并联型一维卷积网络以及迭代加权最小二乘法反演结果如图6a所示，图6b为图6a中圆圈部分局部放大后图像.从图中可以看到，串联网络得到的数据可以很好的拟合真实数据，并联网络得到的数据会在真实值附近有扰动，但两者都要优于IRLS恢复的数据.

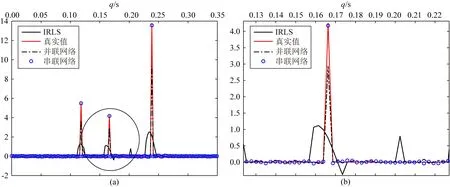
图6 30 Hz数据反演结果(a) 完整结果图； (b) 局部放大图.Fig.6 The inversion result of 30 Hz data(a) Complete graph； (b) Partial graph.

为更好地理解神经网络特征提取的作用，本文将两种网络第3层特征图提出示意于图7.由图7a可看到，串联模型期望提出的特征图最后组合成稀疏的反演结果，其特征图多数是稀疏分布的；而并联模型学习到的是稀疏模型与低分辨率波形的差异，变化较大，因此特征图变化剧烈，如图7b所示，导致其对真实数据的拟合程度要弱于串联模型.图8为两者训练集和测试集的准确率和损失值，从图中观察得到，串联模型和并联模型在20次epoch时几乎收敛，实验发现，随着网络的进一步训练，对多次波的压制效果会有所提升，为此本文epoch设置为80次.从图8中也可以观察得到，串联模型训练集以及测试集的准确率要高于并联模型，损失值要小于并联模型，进一步表明并联模型对数据的拟合程度要弱于串联网络模型.同样的，无论串联网络还是并联网络，两者测试集的准确率都要好于训练集的准确率，测试集的损失值也要小于训练集的损失值，即两者都有较强的泛化能力.

获得主频数据之后，用该频率数据约束其他频率的反演，从而得到所有频率的Radon参数.三种方法反演得到的Radon参数如图9a、b、c所示.观察图9a—c可以得到，网络反演得到的Radon参数能量要比IRLS得到的Radon参数能量更加集中，即网络可以更好的分离一次波和多次波Radon参数.之后由Radon反变换可得到三种方法恢复的地震数据如图9d、e、f，图9g、h、i为三者与真实地震数据值的误差.表3列出了三种反演方法的重构结果，结合图9以及表3，可以观察到串联型网络恢复的数据与真实地震数据的误差最小，其次为并联型网络，两者均要好于IRLS恢复的地震数据.

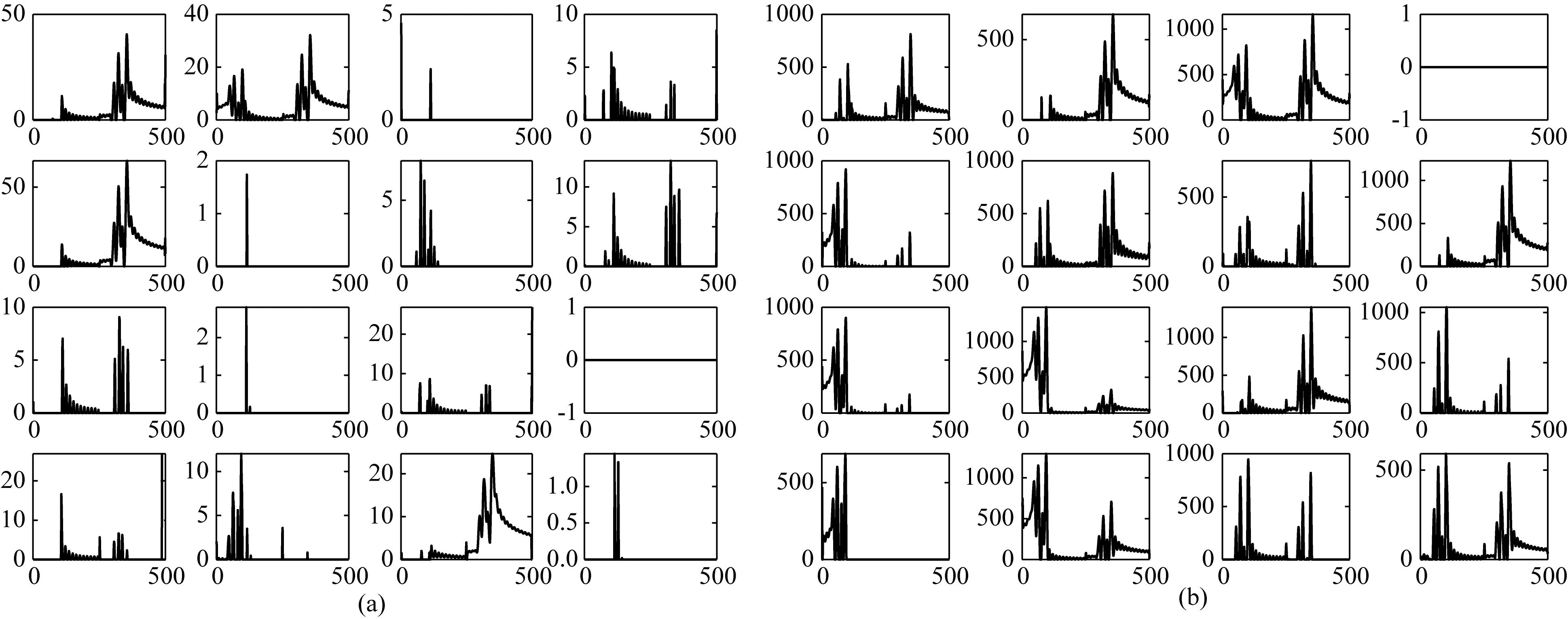
图7 网络特征图(a) 串联网络模型； (b) 并联网络模型.Fig.7 Network characteristic map(a) Series network model； (b) Parallel network model.

图8 网络训练集和测试集的准确率及损失值(a) 网络训练集和测试集的准确率； (b) 网络训练集和测试集的损失值.Fig.8 Accuracy and loss value of network training set and test set(a) Accuracy of network training set and test set； (b) Loss of network training set and test set.

图9 模拟数据对比(a) IRLS方法反演的Radon参数； (b) 串联网络反演的Radon参数； (c) 并联网络反演的Radon参数； (d) IRLS方法恢复的地震数据； (e) 串联网络恢复的地震数据； (f) 并联网络恢复的地震数据； (g) IRLS恢复的地震数据的误差(放大10倍)； (h) 串联型网络恢复的地震数据的误差(放大10倍)； (i) 并联型网络恢复的地震数据的误差(放大10倍).Fig.9 Comparison of synthetic data(a) The Radon model obtained by IRLS； (b) The Radon model obtained by serial 1-D CNN； (c) The Radon model obtained by parallel 1-D CNN； (d) Seismic data obtained by IRLS； (e) Seismic data obtained by serial 1-D CNN； (f) Seismic data obtained by parallel 1-D CNN； (g) The difference between the true and the data obtained by IRLS (10x)； (h) The difference between the true and the data obtained by serial 1-D CNN (10x)； (i) The difference between the true and the data obtained by parallel 1-D CNN (10x).

在三种方法得到Radon域参数之后，滤除一次波参数，经Radon反变换可得到时域多次波数据，从原始数据减去多次波数据即可得到压制多次波后的结果.三种方法估计的一次波数据见图10a、b、c，其与真实一次波数据的误差如图10d、e、f所示.由图10和表3可以得到，串联型网络可以保留更多的一次波信息，其一次波信噪比最高，其次为并联型网络，两者都好于IRLS方法保留的一次波信息.

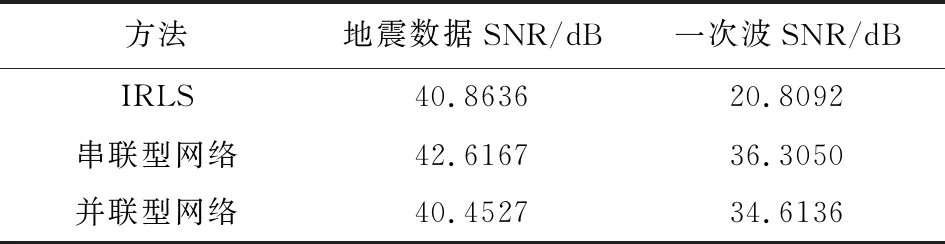
表3 三种方法估计地震数据的信噪比Table 3 The SNR of seismic data estimated by three methods

3.2.3 实际数据

为了进一步验证本文方法的有效性，对如图11a所示动校正三维地震数据进行多次波压制实验.该数据包含13炮数据，每炮25道，每道2501个采样点，采样间隔2 ms.图11b为图11a按炮点距离排序之后的地震数据，可以看到地震数据中含有明显的倾斜多次波.对于实际地震数据，可由最小二乘方法得到Radon参数，之后从中随机抽取一定量的Radon参数组成新的Radon域数据，变换到频域后选取主频对应的Radon参数作为标签数据，其对应的低分辨率共轭解作为输入数据，两者组成数据集.以此生成1100个数据集，其中1000个作为训练集，100个作为测试集.在模拟数据网络训练的基础上，冻结卷积层训练参数，只对网络最后的全连接层进行训练，从而对网络进行微调.

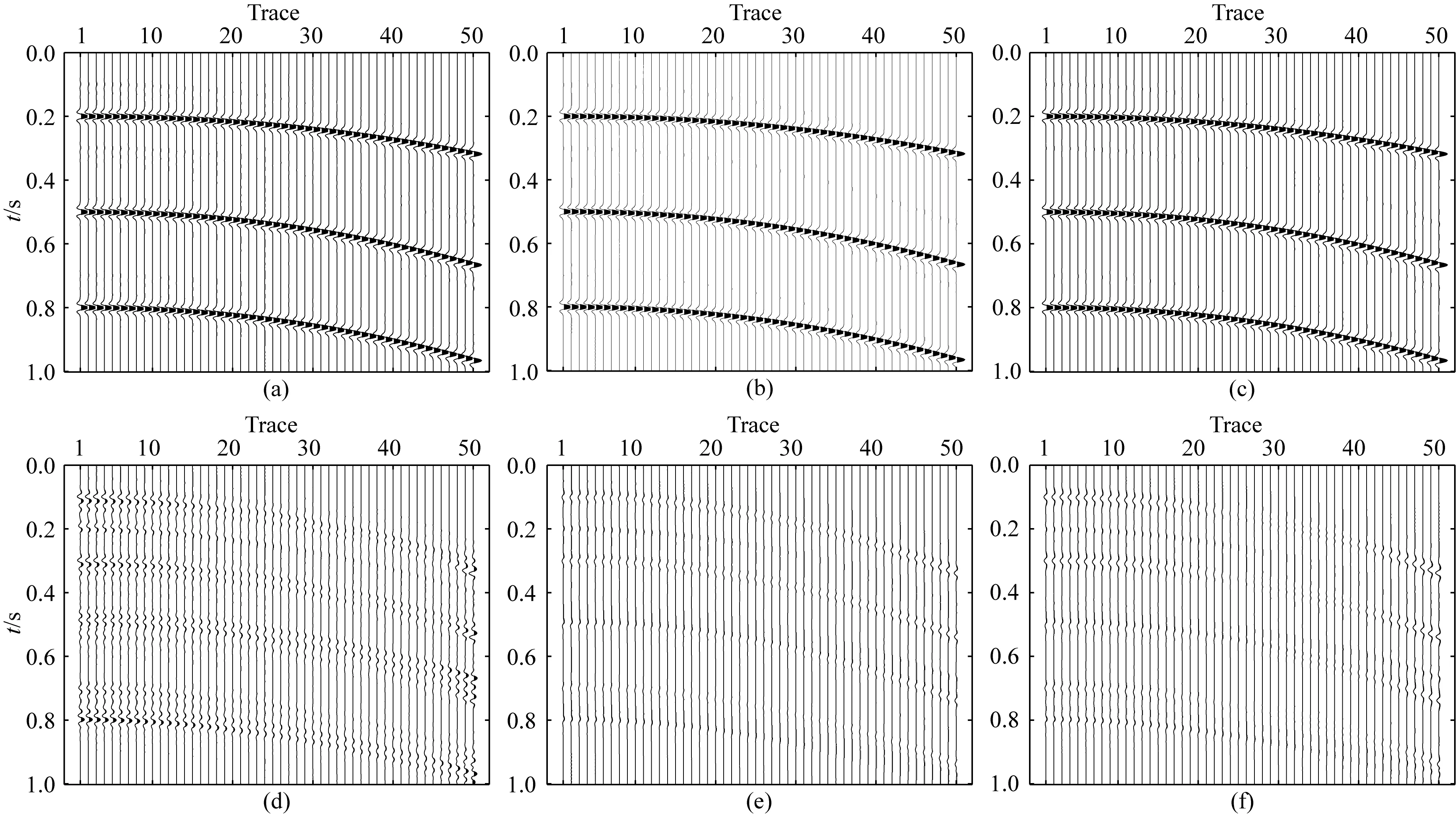
图10 一次波数据对比(a) IRLS方法估计的一次波数据； (b) 串联型网络估计的一次波数据； (c) 并联型网络估计的一次波数据； (d) IRLS方法估计的一次波数据误差(放大10倍)； (e) 串联型网络估计的一次波数据误差(放大10倍)； (f) 并联型网络估计的一次波数据的误差(放大10倍).Fig.10 Comparison of primaries(a) The primaries obtained by IRLS； (b) The primaries obtained by serial 1-D CNN； (c) The primaries obtained by parallel 1-D CNN； (d) The difference between the true and the primaries obtained by IRLS (10x)； (e) The difference between the true and the primaries obtained by serial 1-D CNN (10x)； (f) The difference between the true and the primaries obtained by parallel 1-D CNN(10x).

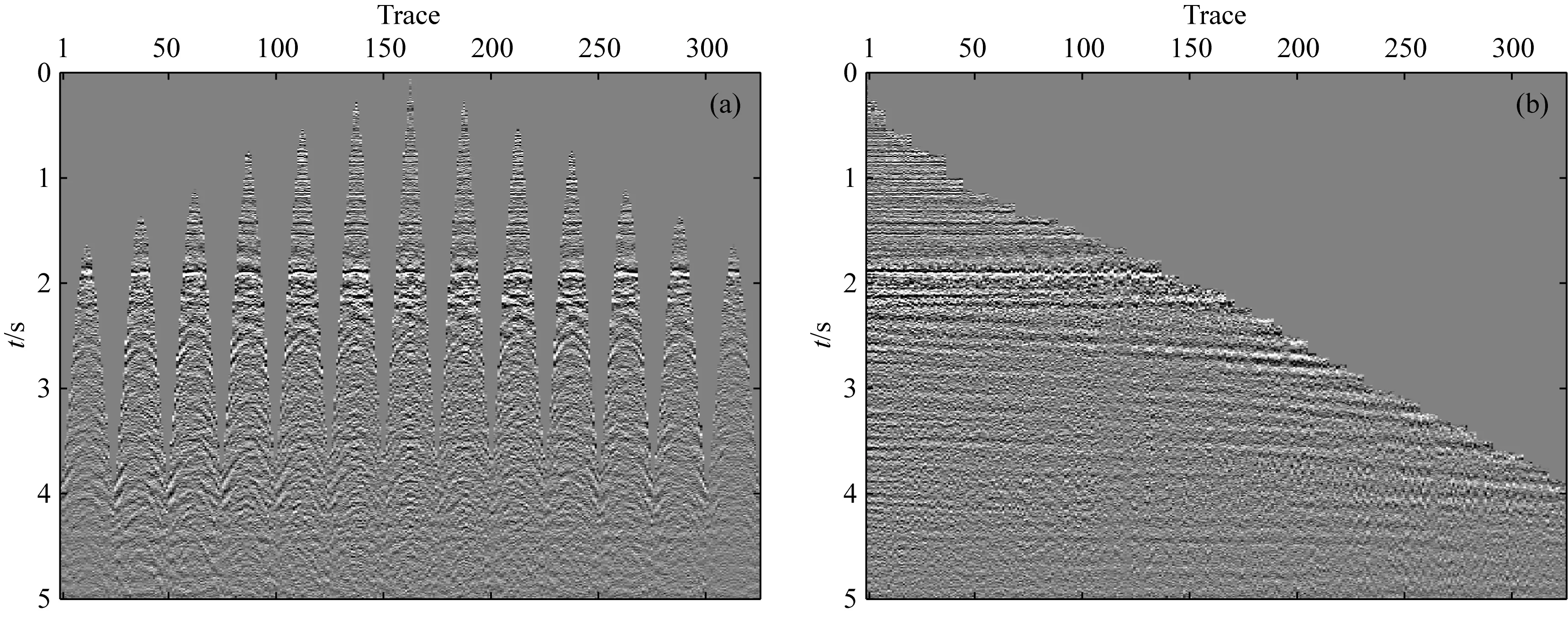
图11 实际地震数据(a) 实际地震数据； (b) 按炮点距排序后的实际地震数据.Fig.11 The field data(a) The field data； (b) The field data sorted by scalar offset.

图12 三种方法处理后的地震数据(a) IRLS方法反演的Radon参数； (b) 串联网络反演的Radon参数； (c) 并联网络反演的Radon参数； (d) IRLS得到的多次波； (e) 串联网络得到的多次波； (f) 并联网络得到的多次波；(g) IRLS方法压制多次波后的数据； (h) 串联网络压制多次波后的数据； (i) 并联网络压制多次波的数据.Fig.12 The field data processed by three methods(a) The Radon model obtained by IRLS； (b) The Radon model obtained by serial 1-D CNN； (c) The Radon model obtained by parallel 1-D CNN； (d) The multiple obtained by IRLS； (e) The multiple obtained by serial 1-D CNN； (f) The multiple obtained by parallel 1-D CNN； (g) The primaries obtained by IRLS； (h) The primaries obtained by serial 1-D CNN； (i) The primaries obtained by parallel 1-D CNN.

采用IRLS、串联型和并联型高分辨率Radon变换分别处理图11所示的实际地震数据，结果如图12所示.图12a—c为三种方法反演得到第8炮数据的Radon参数，可以观察得到，串联网络模型和并联网络模型两者得到的Radon参数分辨率基本相当，都要优于传统IRLS得到的Radon参数分辨率，与模拟数据结果一致.

切除0.15 s以下的Radon参数，可得到多次波对应的Radon参数，经Radon反变换可得到时域多次波数据，如图12d—f所示.从原始数据减去Radon反演得到的多次波数据，即可得到实际地震数据压制多次波后的结果，三种方法压制多次波后的结果如图12g—i所示.观察图12g、h、i中箭头所指部分可以发现，串联网络、并联网络以及传统IRLS都能很好的压制多次波，其中IRLS运行时间为1407 s，串联网络得到单个频率Radon参数后进行多次波压制运行时间为102 s，并联网络得到单个频率Radon参数后进行多次波压制运行时间为101 s，即串并联网络模型运行时间基本相同，都要远小于传统IRLS方法，这是由于传统IRLS计算时需要进行大量的矩阵求逆运算，导致消耗大量时间.

4 结论

本文通过建立Radon变换的卷积模型，借助卷积神经网络的非线性表征能力实现Radon变换的高分辨率反演.建立了串联型和并联型两种神经网络结构，串联型网络实现了Radon变换反褶积算子的功能，而并联型网络学习的是低分辨率解与真实解的残差，两者通过不同的路径实现了低分辨率解到高分辨率解的映射.实验结果证明串联网络模型和并联网络模型都具有较好的应用效果，其中串联网络性能要略优于并联网络模型.

与传统高分辨率Radon变换反演方法相比，基于卷积神经网络的方法不需要借助参数先验信息，只需要为网络送入相应的训练数据，网络就能够学习其中的数据特征，实现所求低分辨率数据到高分辨的映射.在效率方面，网络主要耗时在数据训练过程，而在网络训练好之后，就能够利用网络来快速求解相关问题，即网络可以重复利用.本文通过模拟数据和实际数据的验证，表明基于卷积神经网络的方法来实现高分辨率Radon变换是可行的，神经网络在地震资料领域的运用为高分辨率Radon变换的实现提供了新的发展方向.