时空域同步挤压小波变换联合面波压制方法

林浩然，邢磊,2*，刘怀山,2，李倩倩，张洪茂

1 中国海洋大学海底科学与探测技术教育部重点实验室，青岛 266100 2 青岛海洋科学与技术试点国家实验室海洋矿产资源评价与探测技术功能实验室，青岛 266071

0 引言

面波是地震资料中最为常见的规则干扰波，其是由体波到达地表或介质分界面时，在一定条件下相互干涉并叠加产生的次声波.面波具有低频、低速、强振幅、能量衰减缓慢等特点，在炮集记录中呈近似线性分布，面波的存在严重影响中深层有效信号，显著降低了地震资料的信噪比(王伟奇等，2022).

在地震资料处理过程中，研究人员主要依据面波低频、低视速度的特点，提出了许多压制面波的方法，如高通滤波、FK滤波、Radon域滤波、KL变换域滤波、维纳滤波、SVD滤波、径向道分解滤波、二维时间导数滤波等.这些方法虽具有一定的压制效果，但是往往会对有效信号造成一定程度的损伤.为了获得更好的面波压制效果，提高地震资料信噪比，Deighan和Watts (1997)提出将一维小波变换应用于面波压制工作中.小波变换具有良好时频分辨能力，以及信号奇异性捕获能力(陈永芮等，2021).近年来，在小波变换的基础上，具有更好逼近高维奇异信号能力的多尺度几何分析方法，如脊波(Ridgelet)变换(Candès and Donoho,1999;包乾宗等,2007)、曲波(Curvelet)变换(Candès and Donoho,2004)等被引入面波压制方法研究领域中来.其优越之处在于能更好的利用面波与有效波的视速度差异，捕捉地震信号的奇异特性，同时能更好的刻画图像边缘信息.然而这些时频分析方法都受到海森堡—盖博测不准原理的影响，导致其时频分辨能力受到一定限制.为克服这一问题并提高它们表示非平稳信号的能力，基于锐化时频表示技术(Kodera et al.,1976)和时频重分配思想(Auger and Flandrin,1995)，Daubechies和Maes(1996)、Daubechies等(2011)提出了同步挤压算法，并证明其可以应用于地震数据处理领域.刘晗等(2016)提出将同步挤压小波变换应用于面波压制中.时频重分配算法现阶段已被推广至二维(Yang et al.,2015;Lu et al.,2016)和三维空间(Zhu et al.,2021)中，且有多种变体(Clause et al.,2015;Lu and Yang,2018)和改进(陈文超等,2009;Oberlin and Meignen,2017;Daubechies et al.,2016).

随着处理要求的提高和处理技术的进步，近几年来提出了一些采用多种手段联合压制面波的方法.包乾宗等(2011)提出了联合小波变换和脊波变换的面波压制方法.马见青和李庆春(2011)提出了S变换和TT变换联合压制面波.毕云云等(2017)提出了基于离散曲波变换字典和二维局部离散余弦变换字典联合压制面波的方法.徐阳等(2018)提出了广义S变换与二维离散小波变换联合压制面波方法，该方法对包含面波成分的低频信号再次进行二维离散小波变换，成功提取出了低频信息里包含的有效信号，减少了在有效压制面波干扰的同时对有效反射波的损害.路鹏飞等(2020)提出了曲波变换与傅里叶变换联合压制面波方法.这些多手段联合压制面波的方法，在尽可能保护有效信号的原则下，最大限度地将有效信号和面波分离，进一步提升了地震资料的信噪比.

本文首先在前人研究的基础上将同步挤压小波变换推广至一维空间域，后根据面波干扰频率低、视速度低的特点，采用高精度时频分析方法同步挤压小波时域和空域变换联合压制面波干扰.从时间、空间、频率、波数维度对地震数据进行分析，利用时域同步挤压小波变换结合时频域滤波器将面波与有效信号分离，并对分离出的面波数据体使用空域同步挤压小波变换进行低频有效信号的重提取，通过理论模型测试验证了所提联合方法的有效性，最后通过实际资料处理与一些常用方法的处理结果相比较，证明了所提出的联合方法处理结果信噪比高、保幅性好的优点.

1 方法原理

1.1 一维空间域同步挤压小波变换

同步挤压小波变换(Synchrosqueezing Wavelet Transform, SWT)是由Daubechies等(2011)引入的一种针对非平稳信号的稀疏表示.SWT是基于小波变换的时频重分配，其类似于经验模态分解(Empirical Mode Decomposition, EMD)可以将信号分解为本征模态函数，优于EMD的是，SWT具有更坚实的理论基础(Thakur et al.,2013).

同步挤压算法通过沿频率轴压缩信号的能量来聚焦时频表示，这种后处理方法的时频分辨率极高且具有严格的连续可逆性.该变换可将时变信号分解为如式(1)所示的固有模态：

(1)

式中，Am(t)为瞬时振幅，η(t)代表噪声或误差，M为模态数量，φm(t)为瞬时相位.每个模态的瞬时频率是通过瞬时相位的偏差(Boashash,2003)来计算的，计算方程为：

(2)

现进行空间域同步挤压小波变换推导，给定一空变信号s(x)：

s(x)=A(x)cos(kx+φ0)，(3)

式中，x为波动距离，φ0为初相，A为振幅，(kx+φ0)为信号相位，k为空域角频率也称为角波数：

k=2πξ，(4)

式中，ξ为空间频率.

若需要获取空变信号的空间频率即波数，通常对于空间采样信号通过傅里叶变换来进行空间-波数域变换，得到此空间采样信号的波数谱，其一般定义式为：

(5)

给定母小波函数φ，对空变信号s(x)进行连续小波变换，得到空间-尺度域小波系数Ws(a,b)(Stéphane,2009)：

(6)

式中a为尺度序列，b为空间偏移.根据Plancherel定理，式(6)可以写成波数域表达形式：

(7)

(8)

对Ws(a,b)来说，|Ws(a,b)|表示各空间模态分量的小波系数(Li and Liang,2012)：

(9)

和时间偏移τ一样，当给定一个空间偏移b，信号能量主要沿尺度轴扩散.忽略沿空间轴的能量扩散，对任意Ws(a,b)不为零的尺度-空间点(a,b)，其瞬时空间频率估计表示为：

(10)

当把地震信号同一时刻各道的数据序列看作是反映一定范围内地层及其地质参数，便构成了地震信号的空间序列.地震信号的空间序列与时/深剖面是一一对应的，对于某一探区，不同时刻的空间序列信号对应于相应时/深剖面的不同深度地层位置(党建武和黄建国,2003).

其实际情况下的一般离散型式为：

(11)

式中，i为时序采样点，q为地震记录的道号.

(12)

离散形式的瞬时频率估计为：

(13)

需要注意的是，式(13)中得到的瞬时空间频率估计往往并不是瞬时空间频率本身(只有在输入信号为理想简谐信号时才为瞬时频率)，他是我们用来计算实际空间频率的校正量.

基于上述概念推导出空间同步挤压小波变换(Spatial Domain Synchrosqueezing Wavelet Transform, SSWT)的离散形式为：

(14)

这里把a和ω看成连续函数，空间同步挤压小波变换的连续形式为：

(15)

式中，A(x)={a;Ws(a,x)≠0}.

式(14)、(15)将时频重分配思想推广至空间-波数域，且同步挤压只发生在空间频率轴.

空间域同步挤压小波变换得到的同步挤压空间波数表示，可以使用类似于时域同步挤压小波变换的重构方式，重构得到原始信号：

(16)

如前文所述，野外采集得到的地震信号是时空维度的，通过相速度我们可以建立起地震时域序列与空域序列的联系：

(17)

式中，k为角波数，Ω为角频率，Cp为相速度.由于地震横波如面波具有很强的频散现象其传播速度取相速度，地震体波的相速度和群速度基本相差不大，因此我们可以将式(17)中的相速度近似规定为地震波传播速度，且地震波波速越大，其角波数越小.对于任意t时刻，有：

(18)

式中，Ω、φt为常数.

信号s(x)的连续小波变换(Continuous wavelet transform, CWT)为：

(19)

瞬时空间频率为：

(20)

信号s(x)的SSWT为：

(21)

通过式(19)、(21)建立起了CWT、SSWT与地震波波速之间的联系，并将其展示在空间波数谱中.

由于面波具有视速度低的特性，其在炮集记录中呈现近乎垂直的圆锥状，与有效信号差异明显，因此在对地震数据进行空间域同步挤压小波变换时，面波干扰将主要出现在高波数区，据此可选合适滤波方式对低频段面波干扰和有效信号分离，恢复部分低频有效信号.

1.2 时域同步挤压小波变换与空域同步挤压小波变换联合面波压制方法

综合上述方法原理，针对面波与有效信号的振幅、频率、视速度差异，采用时域同步挤压小波变换与空域同步挤压小波变换联合方法压制面波干扰，具体实现步骤如下：

(1)对目标单炮记录进行频谱分析，确定有效信号和面波干扰的频带.选取最优母小波函数，按道对输入的单炮记录进行时域同步挤压小波正变换(Time Domain Synchrosqueezing Wavelet Transform, TSWT)，得到每道信号对应的时频谱.

(2)根据面波和有效信号在时频谱上能量显示差异，面波能量位于低频段沿时间轴聚集，并呈条带状分布，有效信号能量沿频率轴聚集且沿频率轴正方向收敛，同时结合频谱分析得到的面波与有效信号各自的频带，在时频谱上确定面波分布区.

(3)选择合适时频窗口将面波区域内的数据充零.后进行时域同步挤压小波反变换，得到去除面波干扰的单道时域信号，按道依次重复步骤1～3，即可得到去除面波干扰后的地震记录.同时，将原始单炮记录与此记录匹配相减，得到一次滤波滤除的面波数据体.

(4)对分离出来的低频数据体按时序进行SSWT，选择合适空频窗口将面波区域内的系数充零，反变换为各时刻点对应的空变信号，即提取出在时频域滤波中损伤的部分有效信号.将其叠加到第3步得到的一次滤波后的地震记录中，完成了对面波干扰的联合压制，有效保护了低频段反射波信号.

本文基于Gauss、Bump、Cmhat、Morlet四种母小波函数进行了信号重构(重构误差见图1).结果表明Morlet小波的重构误差远小于其他小波，且能较好地表征信号时频特征(图2).因此本文选用Morlet小波作为母小波函数.

图1 四种母小波函数重构误差比较Fig.1 Comparison of reconstruction errors of four mother wavelet functions

图2 四种母小波函数的TSWT时频谱Fig.2 The time frequency spectrum of TSWT of four mother wavelet functions

2 理论模型测试

为验证所提方法的有效性，首先对正演得到的理论模型进行处理，模型参数见表1.

表1 地层模型参数Table 1 Formation model parameters

图3 理论模型合成记录Fig.3 Theoretical model synthesis record

图3为采用弹性波波场模拟方式生成的理论模型合成记录，单震源单边激发，震源位于地表，二维均匀各项同性介质，共设计了2层水平反射层，采样间隔为1 ms，共有750个采样点，总记录长度为0.75 s，80道接收，最小偏移距0 m，道间距6.25 m，最大偏移距493.75 m.面波主频为20 Hz，反射波主频为50 Hz，整个合成记录不含随机噪声.

图4为理论模型第35道数据进行TSWT后得到的时频谱.时频分析后可得，根据面波与有效信号能量聚集差异和频率差异可以将其区分，但面波与有效信号在部分频段存在重合.因此，当进行面波区充零处理时将损伤部分低频有效信号(徐阳等,2018).

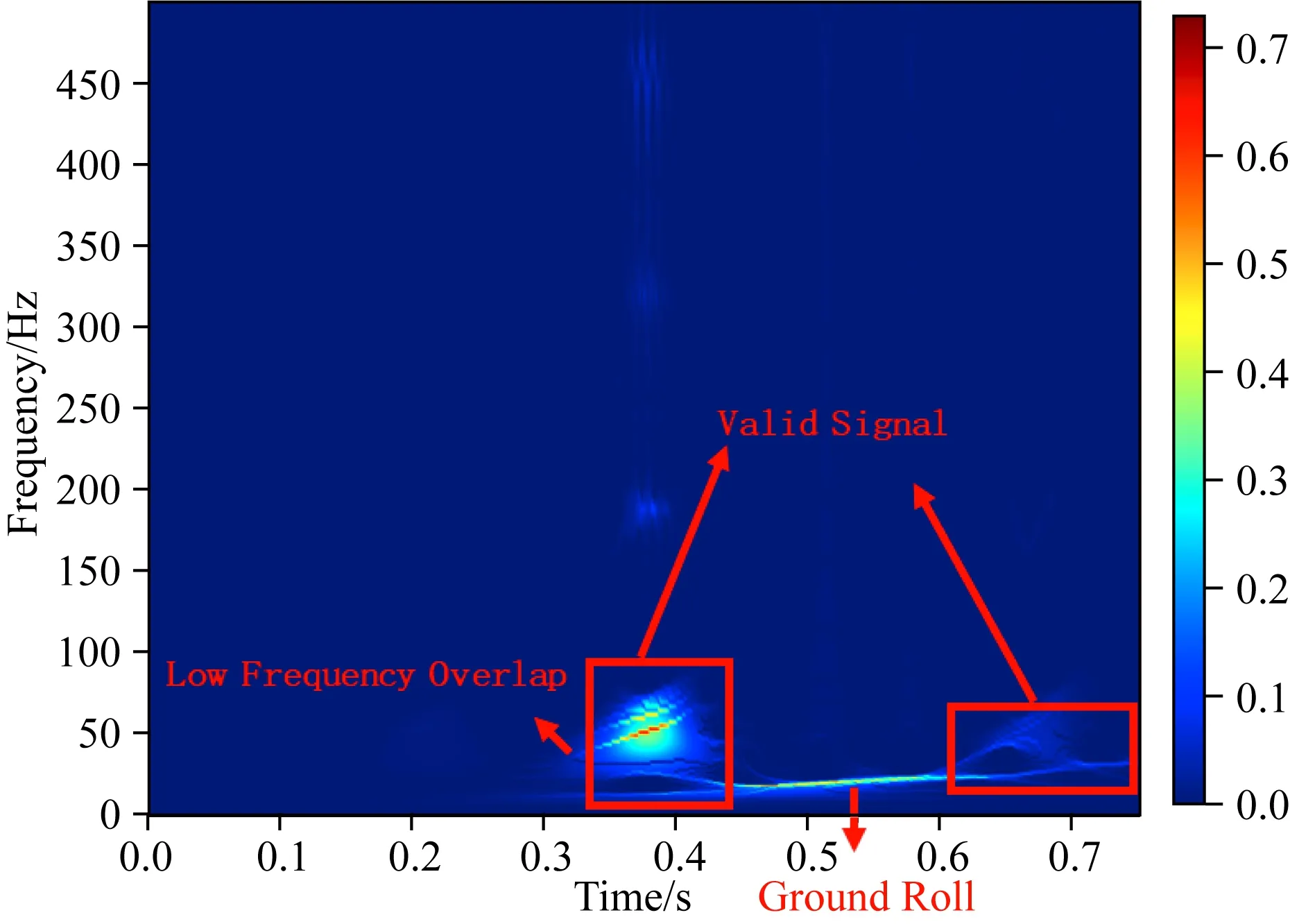
图4 理论模型合成记录第35道的时频谱Fig.4 The time frequency spectrum of channel 35 of theoretical model synthesis record

对理论模型合成记录进行TSWT，确定面波区域并将其充零，得到不含面波干扰的模型记录，如图5a所示.其与原始理论模型合成记录匹配相减，得到一次滤波后滤出的面波干扰，如图5b所示.图5a与图3对比发现，其反射波的同相轴振幅发生了改变，分析可得是由于充零过程导致低频有效信号收到了损伤，这部分有效信号在图5b中也得到了体现.

图5 (a) 经TSWT压制面波后的理论模型记录； (b) TSWT分离出的面波记录； (c) 经SSWT重构出的有效信号； (d) 经联合方法处理所得到的最终记录Fig.5 (a) Record of theoretical model after suppressing ground roll by TSWT； (b) Ground roll separated by TSWT； (c) Valid signal reconstructed by SSWT； (d) Final record of theoretical model after suppressing ground roll by combination method

为恢复被损伤的低频有效信号，对经TSWT后分离出的面波数据体再次按时序对空间序列进行SSWT，得到空间波数谱.如图6所示为0.32 s时刻的空间波数谱对比.

可见对0.32 s的空变信号序列进行同步挤压小波变换后得到的空间波数谱较连续小波变换后能量沿波数轴有了明显的集中，同步挤压小波变换后的空频分辨率远高于连续小波变换.如图6c所示，偏移距在0～100 m能量较强且基本对应同一波数，结合如图5的输入数据不难得到偏移距为0～100 m时有效信号同相轴接近水平，说明其视速度相差不大，因此对应在空间波数谱上的波数接近一致，而面波视速度较低且在同相轴不水平连续，因此在空间波数谱上位于高波数区域且能量轴倾斜发散.这正是在空间波数谱上区分面波和有效信号的依据.对分离的面波数据体按时序进行SSWT，抽取同样时刻数据得到的空间波数谱如图6f所示.在时频域被损伤的有效信号即模型中的两套水平层位的反射波部分能量对应一波数轴刻度集中呈长条状分布，而面波干扰能量团在空间波数谱中高波数区呈倾斜“坚果”状分布，如图6e、f中红框内所示.图6充分说明了SSWT的进行空频分析的可行性和其较连续小波变换更卓越的空频分辨能力.

将面波区充零，并重构即可提取低频段部分被损伤的有效信号.据图6所示，面波干扰得到有效压制同时有效信号的同相轴连续性和形态得到极大改善，与理论模型合成记录接近.同时，本文还使用TSWT对各方法的滤波结果进行了单频地震数据提取，提取出的四组数据从低频至高频涵盖了面波与有效信号的优势频带，并计算了各目标频段以及整个炮集记录的的信噪比(具体算法请见附录).如图7所示，对比原始记录、TSWT滤波后记录和使用联合方法所得各有效频段信噪比结果可得，经联合方法处理后得到的地震记录的分频记录和整体记录的信噪比均高于前者，尤其是在低频段.以上结果证明了SSWT有效恢复在TSWT滤波过程中被损伤的部分反射波，TSWT和SSWT的联合方法提升了地震记录的信噪比.

图6 0.32 s时刻信号空间波数谱对比(a) 面波分离后合成记录的波数-归一化振幅谱； (b) 面波分离后合成记录经空间连续小波变换后得到的空间波数谱； (c) 面波分离后合成记录经SSWT后得到的空间波数谱； (d) 分离出的面波记录的波数-归一化振幅谱； (e) 分离出的面波记录经空间连续小波变换后得到的空间波数谱； (f) 分离出的面波记录经SSWT后得到的空间波数谱.Fig.6 Comparison of spatial wavenumber spectrum of signal at 0.32 s(a) The wavenumber-normalized amplitude spectrum of the synthetic record after ground roll separation； (b) The spatial wavenumber spectrum of the synthetic record after ground roll separation by Spatial Domain Continuous Wavelet Transform (SCWT)； (c) The spatial wavenumber spectrum of the synthetic record after ground roll separation by SSWT； (d) The wavenumber-normalized amplitude spectrum of the ground roll； (e) The spatial wavenumber spectrum of the ground roll by SCWT； (f) The spatial wavenumber spectrum of the ground roll by SSWT.

图8 联合方法面波压制效果对比图(a) Alaska地区第20炮原始记录； (b) 时域同步挤压小波变换压制面波干扰后的记录； (c) 使用联合方法压制面波干扰后的记录.Fig.8 Comparison of ground roll suppression effects of combined method(a) The original record of the 20th source in Alaska；(b) The record after ground roll suppression by TSWT；(c) The record after ground roll suppression by combined method.

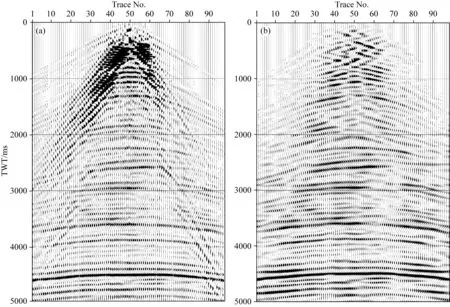
图9 SSWT的输入与输出(a) TSWT后滤除的低频记录； (b) SSWT重构结果.Fig.9 Input and output of SSWT(a) Low frequency record filtered byTSWT；(b) Reconstruction result of SSWT.

图10 时空域同步挤压小波变换切片(a) TSWT滤波前15 Hz频率切片； (b) TSWT滤波后15 Hz频率切片； (c) SSWT滤波前0.001 rad·m-1波数切片； (d) SSWT滤波后0.001 rad·m-1波数切片.Fig.10 Slices of SSWT and TSWT(a) 15 Hz frequency slice before TSWT； (b) 15 Hz frequency slice after TSWT； (c) 0.001 rad·m-1 wavenumber slice before SSWT； (d) 0.001 rad·m-1 wavenumber slice after SSWT.

图11 原始单炮记录第30道TSWT时频谱和分离出的低频数据体第320 ms SSWT空间波数谱(a)和(c) 面波区充零前； (b)和(d) 面波区充零后.Fig.11 The time frequency spectrum of channel 30 of TSWT and spatial wavenumber spectrum at 320 ms of SSWT of the separated low-frequency data(a) and (c) Before zero filling in the ground roll area； (b) and (d) After zero filling in the ground roll area.

图12 3组数据的频谱对比Fig.12 Spectrum comparison of three datasets

3 实际资料处理

本文选取美国Alaska地区某一测线实际数据进行处理，震源采用炸药震源，总道数5568道(曾祥堃，2015).抽取第20炮作为输入单炮记录，每炮共96道，道间距33.53 m，最小偏移距55 m，最大偏移距5525 m，3000个采样点，采样间隔2 ms，记录长度5 s，如图8a所示，面波呈“圆锥状”存在，近偏移距的浅层反射波和远偏移距中、深层反射波与面波干扰重叠，有效信号难以识别，信噪比严重降低.按道依次进行TSWT，得到各道的时频谱，结合数据分析结果，确定面波分布区和时频滤波窗口将其充零.整个记录的面波分离完成后，将得到的不含面波干扰的地震记录(图8b)，与原始记录匹配相减，即可得到经TSWT后滤除的低频数据体，如图9a所示.低频数据体中含有若干条反射波同相轴，结合图10a、b的TSWT滤波前后的15Hz频率切片来看，分析该现象是由于低频段有效信号与面波存在重叠，且为彻底压制面波干扰而扩大使用时频滤波窗口等综合原因导致.

为减少对有效信号的损害，将时域同步挤压小波变换分离出的低频数据体按时序进行SSWT，得到空间波数谱，此时空域的地震数据将转换至空间、波数域中.在空间波数谱中确定面波区将其充零，如图11所示.图10c、d为SSWT滤波前后空频滤波窗口内0.001 rad·m-1波数切片，滤波前对应的重构结果未混有有效信号，滤波后该波数对应的面波干扰基本被完全压制，证实了有效信号与面波干扰视速度差异的SSWT方法的优越性.

有效信号提取结果如图9b所示，可见明显同相轴.将重构结果叠加到TSWT压制面波干扰后的记录中，得到联合面波压制方法的最终结果，如图8c所示.图8c中反射波能量尤其是面波覆盖区和中深层段，显著增强.通过图12中3组数据频谱对比，可以更直观地看出使用联合方法后，低频段能量被有效恢复.根据图13信噪比对比结果来看，经联合方法处理后的低频段数据以及整体地震数据的信噪比均高于原始数据和单一使用TSWT处理后的结果.从实际资料的处理结果可以看出本文所述面波压制联合方法在有效压制面波的同时能极大程度地保留低频段有效信号.

4 讨论

在这一部分中，主要讨论时域和空域同步挤压小波变换联合方法的优势和通过实际结果呈现出的该方法尚未解决的缺点以及未来的研究方向.

4.1 联合方法实际应用优势

时域和空域同步挤压小波变换联合面波压制方法是高精度时频分析方法在地震资料处理面波压制领域的综合应用.如前文分析，理论上使用TSWT一次滤波后可以将面波彻底分离，再对提取出的面波进行SSWT，重提取部分低频有效信号.对于实际数据时频分析来说，精确定位面波区，彻底分离面波干扰，避免过多损伤非目标频段的有效信号才是主要目的.

时域同步挤压算法可以有效解决传统时频分析方法能量沿频率轴发散的问题.虽然未使用同步挤压算法的时频分析方法得到的时频谱看起来能量成团分布，但是相邻能量出现多处重叠，这导致以往的时频域滤波方法为了彻底分离面波，存在扩大滤波窗口(系数充零区)的现象，会损伤非目标频段的有效信号，而TSWT会有效改善这一问题，但仍未彻底解决.因此时频窗口选择范围越精确，信号的保幅性越好，虽然这会牺牲一定的计算效率.

本文所提出的SSWT重提取在一次滤波中被滤除的有效信号，充分利用了反射波和面波的视速度差异.结合图5c和图9b的重构结果，是联合方法中SSWT可以恢复部分被损伤的低频有效信号的直接证据，这一优势是单一方法和其他联合面波压制方法不具备的.图14的四种方法处理结果对比再次证实了上述观点.图14a中可见基于视速度差异的FK滤波对面波压制效果较为彻底但是会损伤浅层有效信号如直达波，同时会产生大量空间假频；图14b和图14c对比证明了TSWT的面波压制能力和保幅能力优于CWT但还是丢失了部分中深层有效信号；图14d使用联合方法得到的处理结果面波压制力和保幅性兼优，压制效果最为理想.

4.2 联合方法的缺点及未来研究方向

如上述分析在使用同步挤压小波变换后对时频、空频滤波窗口内系数充零时没有寻找到最优处理方式.本研究下一步可以改进滤波方式，在阈值迭代去噪、自适应时窗、深度学习等领域进行探索.

在SSWT重构有效信号环节，主要依据的是面波和有效信号视速度的差异即在地震剖面中同相轴倾斜程度不同.然而由于面波的频散效应部分相邻道往往会形成低倾角同相轴，这些假层位同相轴振幅往往较小，但会不可避免的出现在重构结果中，如图5c所示.如何去除这些假层位低倾角同相轴是未来研究的重点问题.

在图13中45 Hz的信噪比对比中联合方法处理后的地震数据信噪比略低于仅使用TSWT处理.我们抽取了三组45 Hz地震数据及其时频能量切片，发现不存在明显的面波干扰，如图15b、e所示，因此判断是由于重构误差或是信噪比算法误差所致.联合方法处理得到的整炮地震记录信噪比是最高的未与理论相背.

5 结论

本文将同步挤压小波变换推广至空间域，并对其实现过程进行了公式推导与实际验证.并通过时域与空域同步挤压小波变换联合方法压制面波干扰，并对理论和实际资料进行处理，调整最优参数，取得了较好的处理效果.该联合方法的优点在于：

(1)使用高精度时频分析方法时域同步挤压小波变换，结合时频域滤波与空频域滤波，对面波压制彻底.

(2)对一次滤波后分离的面波干扰再次进行空域同步挤压小波变换，从空间、波数域中判别有效信息与面波干扰的地震属性差异，能有效提取部分低频反射波，切实保护了低频段有效信息，提高了地震数据的信噪比.

(3)本文方法的实现，证明了在面波压制中进行时空域滤波，从而恢复低频段有效信号的方法的优越性.

图13 野外单炮记录各有效频段信噪比对比Fig.13 Comparison of signal-to-noise ratio of each valid frequency band recorded by actualdata

图14 四种面波压制方法实际资料处理结果对比(a) FK滤波； (b) CWT； (c) TSWT； (d) TSWT & SSWT.Fig.14 Comparison of actual data processing results of four ground roll suppression methods(a) FK filtering； (b) CWT； (c) TSWT； (d) TSWT & SSWT.

图15 实际记录45 Hz切片(a) TSWT 45 Hz 切片； (b) SSWT重构结果45 Hz切片； (c) 联合方法最终记录45 Hz切片； (d) TSWT 45 Hz时频谱； (e) SSWT重构结果 45 Hz时频谱； (f) 联合方法最终记录45 Hz时频谱.Fig.15 45 Hz slices of actual record(a) TSWT； (b) Reconstruction result of SSWT； (c) Final record with combination method； (d) The time frequency spectrum of TSWT at 45 Hz； (e) The time frequency spectrum of reconstruction result of SSWT at 45 Hz； (f) The time frequency spectrum of final record with combination method at 45 Hz.

附录

本文计算信噪比的方法为相关时间移法及其改进算法(牛聪等,2006;王红玲,2007).

Qi,i+1(ti,i+1)=max{Qi,i+1(τ)}，(A1)

其中相邻道间最大的互相关值Qi,i+1(ti,i+1)作为信号的功率谱：

(A2)

(A3)

N为地震道数，使用各道的自相关值作为地震记录的总能量，则噪声的能量为：

(A4)

信噪比为：

(A5)

当对含有面波干扰的原始地震记录进行信噪比估算时，需要将使用联合方法滤波后的最终记录作为有效信号能量Es的输入记录.总能量E则用原始地震记录通过相关时移法计算.