机器人TIG焊接的焊缝形貌遗传神经网络预测

吴月玉，张 弓，林群煦，侯至丞，杨文林

（1.广州中国科学院先进技术研究所，广州 511458；2.五邑大学 轨道交通学院，江门 529020）

0 引言

机器人焊接是一个典型的多输入多输出非线性时变系统。焊接工艺是工业制造中不可缺少的重要组成部分[1]。钨极惰性气体保护焊（TIG）是最常用的弧焊工艺之一，是在惰性气体的保护下，通过非消耗性钨电极和工件之间产生电弧熔化母材和填充焊丝实现焊接的一种方法[2]。随着焊接产品制造技术自动化、柔性化和智能化的提高，焊接工艺参数的选择必须经过进一步优化，才能在给定的生产率下获得理想的焊缝[3]。各焊接工艺参数之间的高度复杂耦合性使求解最佳焊接工艺成为一个难题[4]。

传统的焊接工艺需要通过大量试验制定，成本高且实验结果不确定性很大[5]。因此，国内外很多学者建立焊接工艺参数和焊缝几何形状之间的数学模型来控制和优化焊接过程。Yang[6]等建立了多元线性回归模型对埋弧焊的焊缝宽度、余高和熔深进行预测；Kim[7]等利用BP神经网络方法预测多道次焊接的焊缝余高和焊缝宽度；Marina[8]等利用人工神经网络预测奥氏体不锈钢焊缝的铁素体含量、熔宽、余高和熔深；Yin[9]等建立深度网络模型对5083铝合金双丝CMT焊接焊缝的熔深、熔宽和余高进行预测；陈子琴[10]等用焊接特征信息图像所提取的9组特征信息作为输入建立含两个隐藏层的贝叶斯神经网络对焊件背面的宽度进行预测；Yang[11]等利用决策树和贝叶斯神经网络研究了搅拌摩擦焊气孔形成条件；Parikshit[12]等利用遗传算法替代BP神经网络的梯度下降法搜索神经网络的最优权值后建立神经网络预测TIG焊接焊缝的正面高度、背面宽度、背面高度和背面宽度。虽然这些模型对焊缝形貌预测具有一定的作用，但由于影响焊缝形成的因素众多且复杂，各个焊接工艺参数之间高度耦合，导致预测的精度不是很高且泛化能力不是很强。此外，传统BP神经网络存在收敛速度慢、训练时间长、容易陷入局部最小值的问题[13]；而利用遗传算法替代BP神经网络的梯度下降法虽克服了BP神经网络易陷入局部最小点的问题但仍存在遗传迭代次数多、训练时间过长的问题。

为了解决上述问题并进一步提高焊缝形貌预测模型的预测精度和泛化能力，本文通过试错实验确定BP神经网络的拓扑结构，其次利用遗传算法确定BP神经网络初始的权值和阈值后建立TIG焊接的焊缝形貌预测模型,最后通过一些测试实例对比和验证该模型的性能。

1 TIG焊接过程的特征参数

焊缝几何形状在确定焊缝的质量方面至关重要，而焊接机器人的各个焊接工艺参数都在一定程度上影响焊缝几何形状的形成。图1是TIG焊的原理示意图[14]，图2是TIG焊接的焊缝主要形貌几何参数示意图。

图1 TIG焊原理示意图

图2 焊缝几何参数示意图

TIG焊接过程的输入工艺参数（如焊接速度、送丝速度、阴极清洗率、间隙、焊接电流)与输出焊缝的形貌几何参数（如正面高度FH、正面宽度FW、背面高度BH、背面宽度BW）之间的映射关系如图3所示。

图3 TIG焊接输入输出参数映射示意图

为了提高建模的效率，本文利用全因子实验设计(DOE)的样本数据作为训练模型的数据，每个输入变量考虑两个水平如表1所示，实验组合为32组实验。另外选用33组实验数据验证模型的预测精度和泛化能力；需要指出的是，上述所提及的训练和测试模型的数据均是从文献[15]中收集所得。

表1 输入焊接参数及其范围

2 建立GA优化的BP预测模型

2.1 BP神经网络的建立

BP神经网络具有较强的非线性映射能力和容错能力[16]；已被广泛运用于各种焊接参数的非线性预测中。所建立的5输入4输出的TIG焊接焊缝形貌BP神经网络拓扑结构如图4所示。

图4 TIG焊接过程BP神经网络拓扑结构

BP神经网络主要包含信号前向传播和反向传播两个过程，每一层中特定神经元的示意图如图5所示，分别为输入层的第个神经元、隐藏层的第个神经元和输出层的第个神经元[12]，BP神经网络各层的各个神经元的运算过程如图5所示。

图5 每一层中特定神经元的示意图

信号前向传播具体运算过程如下：

1）位于输入层的第j个神经元的输出可确定为：

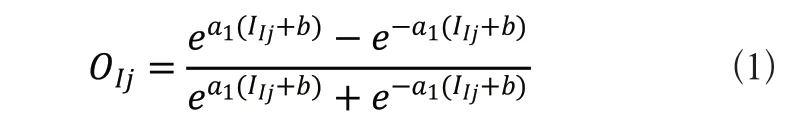
其中a1是传递函数常数，b为偏置值，IIj为位于输入层的第j是个神经元的输入。

2）位于隐含层上的第k个神经元的输入可计算如下：

其中vjk表示输入层第j个神经元与隐含层第k个神经元的连接权值。隐藏层的第k个神经元的输出如下：

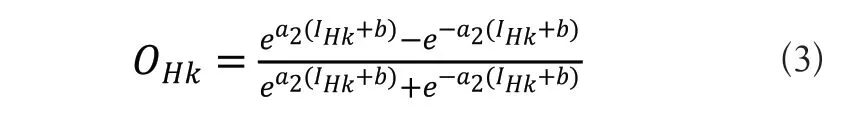
其中a2为传递函数常数，b为偏置值，IHk为隐藏层的第个神经元的输入。

3）位于输出层的第m个神经元的输入如式(4)所示：

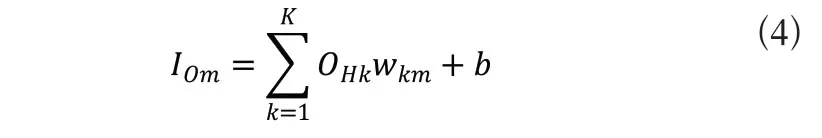
其中wkm表示隐藏层的第k个神经元与输出层第m个神经元的连接权值。输出层的第m个神经元的输出如式(5)所示：

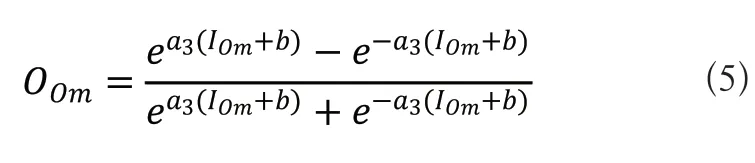
其中a3为传递函数常数，b为偏置值，IOm为位于输出层的第m个神经元的输入。

4）信号反向传播的运算过程如下：

（1）使用随机梯度下降算法如式(6)所示最小化损失函数：

其中J(θ)为损失函数，θ为参数，a为学习率。

（2）损失函数为：

其中p为训练数据的个数，n为输出向量中变量的个数。yij为输入第i个样本时第j个节点的期望输出值；y′ij为输入第i个样本时第j个输出节点的输出值。

为了对神经网络进行适当的训练和测试，训练样本数据和测试样本数据所列的实验焊接数据归一化，归一化范围为[0，1]。设置Sigmoid 函数为隐藏层的传递函数，设置Purelin 函数为输出层的传递函数，设置学习率为0.05，网络训练目标为0.01，最大迭代次数设置为20000。

为了确定BP神经网络的隐藏层的最佳神经元节点数，在4～26之间通过试错实验确定，每个网络重复5次，并记录测试样本MSE最低时所对应的网络性能参数。隐藏层神经元数目不同时所对应的网络性能如表2所示，结果表明隐藏层神经元数目的增加并不能保证均方差的降低。考虑网络的泛化能力与网络的逼近能力，通过对比验证，选取隐藏层神经元数为22即确定BP神经网络结构为5-22-4。

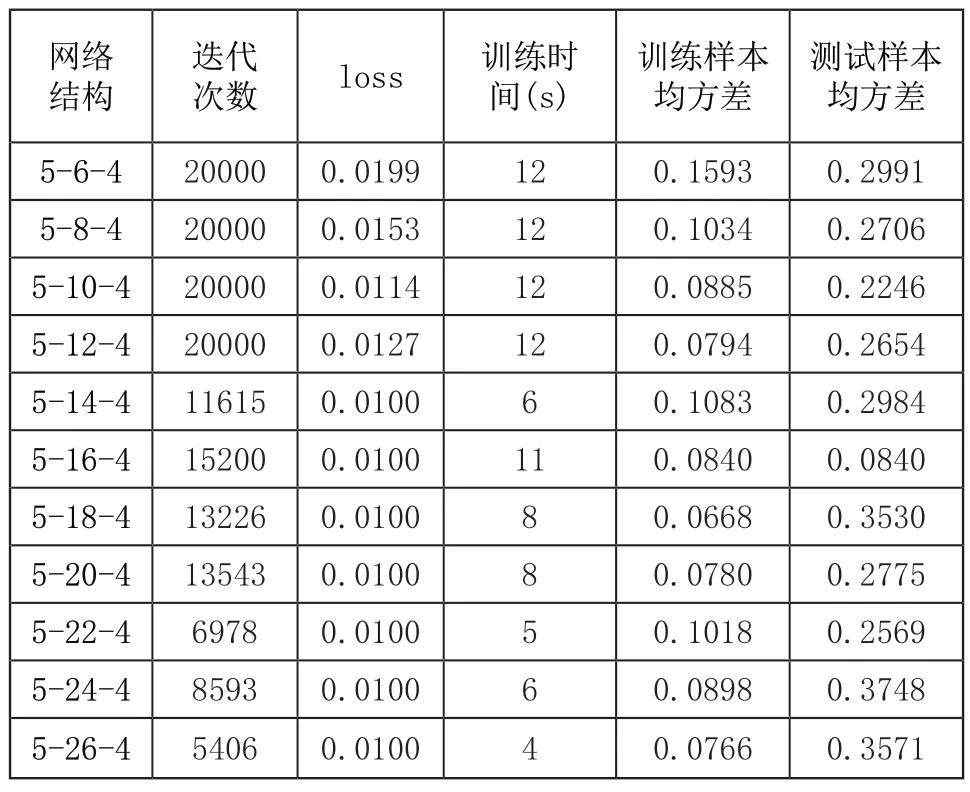
表2 用于TIG焊接过程建模的各种反向传播网络

2.2 GA和BP的结合

遗传算法（genetic algorithm，GA）是基于生物界适者生存、优胜劣汰的进化规律实现全局空间优化搜索的算法[17]，将待优化参数转换成编码串联到群体中，再按照所选择的适应度函数对编码的参数进行若干代的交叉、变异和选择操作最终获得适应度最高的个体[18,19]。

利用遗传算法优化反向传播神经网络（back propagation neural network，BP）的初始权值和阈值的流程如下：

1）设置GA的种群个体数50、遗传迭代代数为20，交叉率为0.5，变异率为0.005。根据2.1节所确定的BP神经网络网络设置各层的初始权值和阈值的个数（如表3所示）后按实数编码的方式将其对应于染色体每个基因位；然后将[-0.5，0.5]之间的数值随机赋予BP神经网络的连接权值和阈值即生成初始种群。

表3 BP神经网络的权值和阈值的个数

2）利用神经网络训练样本的均方差的倒数计算GA当前种群的每个个体的适应度值，即：

其中，fi为个体i的适应度值；k为输出层节点数；ymn为输入第m个样本时第n个节点的期望输出值；y′mn为输入第m个样本时第n个输出节点的输出值。

3）重复进行选择、交叉、变异操作达到20次后将最优个体所对应的值分解后赋给BP神经网络作为它的初始权值和阈值；最后导入训练样本对BP神经网络进行训练并保存最优的BP神经网络模型。

4）利用测试样本对所保存的网络模型的预测精度和泛化能力进行测试和验证。

3 焊缝形貌的预测

3.1 训练网络模型

将训练样本归一化后导入到GA-BP网络模型中进行训练。寻找最优适应度个体过程中种群的平均适应度值的变化如图6所示，平均适应度值随着遗传进化代数的增加而增大，在第11代时平均适应度值最大，进化到20代时停止遗传操作。将最优个体分解后赋给BP神经网络作为初始权值和 值后训练BP神经网络，优化后的BP神经网络训练过程的损失函数变化如图7所示，网络训练到401步时达到要求的训练精度，迭代训练终止。

图6 平均适应度值变化曲线

图7 训练误差变化曲线

3.2 仿真验证与分析

为了检验本研究建立的GA-BP的TIG焊接的焊接工艺参数与焊缝形貌关系回归模型的性能，采用传统BP神经网络（BP）、遗传算法优化BP神经网络（GA-BP）进行对比试验。两种算法中的BP神经网络的训练模型的目标精度均为0.01，学习率均为0.05；将训练样本进行归一化处理后分别导入BP神经网络模型和GA优化后的BP网络模型中进行训练后并保存最优模型；再将测试样本进行归一化处理后导入到所训练好的两种模型中，最后将预测结果进行反归一化处理即可得到对应焊缝的正面高度FH、正面宽度FW、背面高度BH、背面宽度BW的预测值，预测结果如图8所示。表4为BP神经网络模型和GA-BP神经网络模型的决定系数表，表5为BP神经网络模型、GA-NN神经网络模型和GA-BP神经网络模型的平均绝对百分比误差表。

由图8可以看出BP神经网络模型和GA优化的BP网络模型都能较好地预测TIG焊接的焊缝主要形貌参数；通过表4和表5的数据分析可知，遗传算法优化BP神经网络模型测试得到的平均绝对百分比误差比较小，且决定系数比较大，说明遗传神经网络预测效果优于传统BP神经网络，预测精度更高，泛化能力更强，选用遗传算法优化BP神经网络模型可以建立更有效的TIG焊接的焊接工艺参数与焊缝形貌关系回归模型。

图8 预测效果对比图

表4 两种模型决定系数（R2）表

由表5可知本方法训练时只需经过20次遗传迭代获取初始权值和阈值后结合BP神经网络的401次梯度下降迭代训练达到均方差目标为0.01时，同一测试集的部分响应可比文献[8]中的GA-NN预测方法所预测的FH、FW、BW的平均绝对百分比误差分别减少12.057%、5.442%、6.703%，适应性更强，预测精度更高。GA-BP焊缝形貌预测结果的优劣在很大程度上取决于BP网络的好坏。由于多输出BP神经网路的损失函数的局限性，所预测的背面高度BH的预测精度有待提高。后期可通过改进损失函数和优化网络训练集等方式对模型的训练过程进行优化提高BH的预测精度。

表5 三种模型平均绝对百分比误差（MAPE）

4 结语

1）利用全因子实验设计可以大量减少试验次数和训练的样本容量，保持其代表性的同时减少训练模型所需的时间。

2）仿真验证结果表明，与传统的BP神经网络相比，通过遗传算法优化BP神经网络的初始权值和阈值后的BP神经网络模型的预测精度更高，适应性更强，能有效预测TIG焊接的形貌特征参数。

3）根据本研究建立的TIG焊接的焊接工艺参数与焊缝形貌关系回归模型可以较好地预测TIG焊接的焊缝正面高度、正面宽度、背面高度和背面宽度，从而为TIG焊接地焊接工艺参数调优提供理论基础。