五自由度机械臂运动分析及轨迹规划

谢 嘉，窦良浩，李永国，梁锦涛

(上海海洋大学 工程学院，上海 201306)

0 引言

21世纪以来，社会发展愈来愈智能化信息化，人工成本的升高，以及社会生产生活对于效率和精度要求越来越高，以机器人操作代替人工操作的方式普遍存在于各行各业。

其中在服务行业，服务机器人凭借着廉价、优秀的交互能力和良好的执行能力在家庭服务，行业咨询，消防救险，物资输送等行业大放异彩。然而带有机械臂的服务类机器人，除了能够主人之间的语言交互，还能够根据要求做出相应的回应，例如，端茶倒水，捏肩等。

本文在以设计家庭服务机器人的基础上，针对性研究机器臂，探讨研究多自由度状态下机械臂运动与轨迹以及工作空间问题。

从人类手臂的结构来说，三自由度手臂已满足正常的工作需求，考虑到家庭服务环境可能较为狭窄三自由度手臂在人体关节正常活动范围内的工作空间无法满足机器人复杂日常工作需求[1]。出于节约机器人工作空间以及适应更加复杂工作要求的目的，本文设计一种五自由度家庭服务机器人的手臂。针对于机器人的手臂，完成了对于五自由度机器臂的运动学分析和轨迹规划，为后续控制手臂完成捏肩倒水等工作提供理论依据。

1 机械手臂的结构与运动学分析

1.1 机械手臂的结构

本研究设计的机械臂具有5个关节自由度，可以很好的完成期待目标动作。机械机构如图1所示，所有零件的设计装配在SolidWorks中完成，参考人类手臂结构，设计五自由度的机械臂机构。肩舵机通过联轴器与肩部直步进电机链接，完成肩部的旋转与摆动的相关动作。同样肘部拥有肘舵机与肘部步进电机，提供肘部的旋转与弯曲，在手臂末端提供一个小型电机方便微调末端手腕的姿势。

图1 机械臂结构示意图

在机械臂的自由度选择上，一般来说机械臂的自由度并不需要太多，但是考虑到在家庭环境中机械臂需要对主人的要求做出回应。针对于较为狭窄的家庭环境来说，五个自由度的机械臂的灵活性更好，工作空间更大，适用于家庭环境内。

依据本文机械臂的基本结构，采用常用且经典的D-H坐标变换法，完成对机械臂的三维模型的建立。根据方法基本要求建立连杆坐标系如图2所示，5自由度机器臂的D-H参数及各关节运动范围如表1所示。

表1 机器人D-H连杆参数表

图2 机器人连杆坐标系

其中D-H建模方法有两种，一种是标准的D-H建模法，另一种是改进的D-H建模法，两种方法最大的区别就是在于坐标系{i}的位置不同。标准的D-H法的坐标系{i}建立在i+1的关节之上而改进后的D-H法的坐标系{i}建立在i+1上。对比两种D-H法由于坐标系建立的不同随之带来的则是D-H表参数的不同。两种方法本质上没有太大区别，在运动学分析时采用标准的D-H法，在MATLAB中采用修改的D-H法做两种方法的熟悉与运用。

从首先确定的第一个关节到下一个关节的变换，实际上是两个关节坐标系之间的变换。因此通过这样的坐标系变换方式，可以推导机器人的总变换矩阵。例如确定基座作为起始，由基座变换至第一个关节，在此基础上在变换至第二个关节，结合所有变换得到的变换矩阵为总变换矩阵。

而相邻连杆坐标系i相对于i-1的变换i+1iT的齐次坐标变换矩阵通式为：

其中：sθi=sinθi，cθ1=cosθi。

由此i与i-1连杆坐标系之间的齐次坐标变换矩阵通式，可以得到01T12T23T34T45T的齐次变换矩阵。

1.2 运动学分析

作为家庭服务机器人的机械手臂，在工作时需要对主人的指令做出回应，因此对于机械臂的运动学分析极其重要。机械臂运动学分析包含了机械臂正向运动学分析和逆向运动学分析[2]。

1.2.1 正运动学分析

采用D-H法根据表一中提供的相关数据，利用齐次变换矩阵通式可得到机器人基座坐标系O0与末端执行器坐标系O5的正运动学方程[3]为：

经过齐次变换矩阵得到的正运动学方程，其中未知数为各关节角度。则通过式(1)可推导末端关节位姿（n，o，a，p）与关节变量(θ1，θ2，θ3，θ4，θ5，)之间的关系。其中，n，o，a三个向量表示末端执行器相对于基座参考坐标系的姿态，p向量则表示末端执行器在基座参考系中的位置[4]。

其中：

由位姿矩阵的定义，机器人末端的姿态和坐标分别为：

因此当给定确定的θ，机器臂位姿总是确定的。

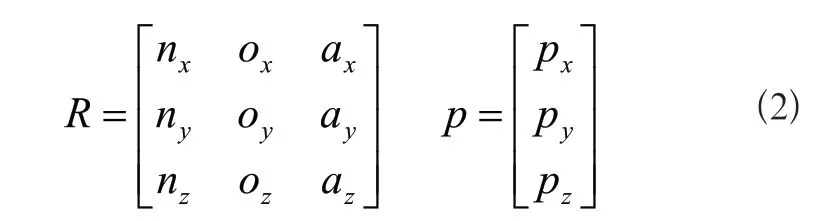
1.2.2 逆运动学分析

现已知机器人的期望位姿，求解每个关节值，这就是逆运动学所要研究的，也是运动学中最重要的。

已知：

本文采用反变换法求解。

1）求解θ1同时将式(3)中左边同乘以消去其中一个变量得：

另其中该式两端(3，3)（3，4）元素相等可解的：

另其中(1，4)和(2，4)两端元素相等解得：

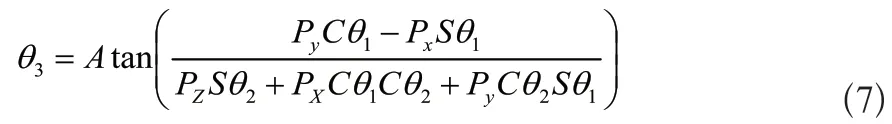
4）求解θ4。对式(6)中(1，3)和(3，3)元素分别对应相等得：

5）求解θ5。

2 基于MATLAB机械臂的运动学仿真

2.1 机械臂建模

对于机械臂的运动学仿真方法，本文在MATLAB软件环境下，通过调用机器人工具箱Robotics Tool中的函数算法，可以得到符合研究目标的运动学模型。

由表一中的机器臂的各个参数，编写相应程序，采用修改后的D-H法编写的程序如下，并命名该手臂为mdl_p5dof。

依次建立五个杆件数学模型L1，L2，L3，L4，L5

连接各关节获得的机械臂的模型如图3所示。

图3 五自由度机械臂运动学模型

2.2 机械臂的正逆运动学仿真分析

对于机器臂的正运动学的验证，我们通过基于Robotics Tool机器人工具箱关于机械臂正运动学的算法，在每个目标关节变量允许的变化范围内随机选取任意角度，例如：

选取(θ1，θ2，θ3，θ4，θ5)=(π/6，π/3，-π/6，π/3，π/3)，将这些数据代入式(2)中得到机器人末端位姿矩阵为：

本文通过对比MATLAB中基于fkine函数编程求解得到的机器人末端位姿矩阵与前文由标准D-H法得到的末端位姿矩阵验证正运动学的正确性。由于在计算过程中舍入位的差异，导致最后二者求解末端位姿矩阵由些许差异，但并不影响结论的正确性。

在逆运动学求解过程中Robotics Toolbox机器人工具箱提供两种求逆向运动学的函数。其中ikine6s()函数一般求解于6轴机械臂而ikine()可默认6轴机器臂也可用于非6轴机械臂的求解。本文设计为五轴机械臂，将采用ikine()函数，已知量设置为正运动求解得到的位姿矩阵，在MATLAB通过ikine()函数求解逆运动。求解得到的关节变量为：

在MATLAB中求解的结果与关节已知量之间不完全相同，这是因为机器人逆运动计算过程中存在多重的计算结果，而ikine()只会自动选取其中一组逆解[5]。由MATLAB得到的逆解不一定是最适合于该设计情况下的最优解，现实设计时需要结合工作任务及各关节变量范围取最适合逆解。

3 轨迹规划

轨迹规划指选取机器人手臂末端执行端在工作轨迹上的若干点，通过运动学逆解得出各个关节的运动规律，在关节空间内选取相应点进行插值并建立运动方程，得到光滑的连续拟合曲线[6]。对机械臂进行轨迹规划的时通常分为两种方法：关节空间轨迹规划和笛卡尔空间轨迹规划[7]。关节空间轨迹规划针对于各个关节，通过多各个关节进行插值拟合，保证各个关节的连续性与稳定性，但并不直接对末端执行器的轨迹直接进行规划。互补的，笛卡尔空间轨迹规划并没有对机器臂关节规划分析，直接给出末端执行器的轨迹，目的在于确保机械臂末端执行器在规定的轨迹上运动，但是容易出现特殊关节。本文通过模型分析各关节运动规律，求解关节角度给出关节空间的轨迹规划，并分析笛卡尔空间轨迹规划获得该机器臂的位移轨迹。

3.1 关节空间轨迹规划

关节空间轨迹规划通过设置起始点与终点，在其之间插入相当关节数的轨迹点，由于约束条件限制选择最优的插值函数，求解各个关节的变量并获得光滑的拟合曲线。在Robotics Toolbox机器人工具箱中利用jtraj()函数，设置关节起始点为（[40 50 -30 -30 -10]*du），终点处设置为（[40 10 -60 -30 30]*du），这样机械臂的末端执行器起点与终点设置完毕。将关节空间轨迹规划时间设置为8秒，步长为0.05，得到轨迹规划图如图4所示。

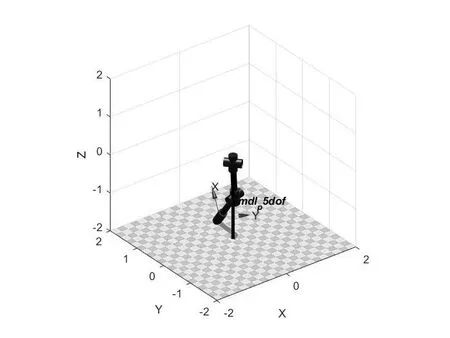
图4 关节空间运动轨迹图

各个关节随时间变化的角位移，角速度和角加速度的曲线如图5所示。

图5 各个关节角度，角速度，角加速度曲线

图五中各个关节角度，角速度和角加速度随时间变化曲线图光滑连续无凸起，关节角度在变量允许范围内连续变化，角速度起始点为0且在四秒时角速度达到最大。而角加速度在2秒时达到最大并在4秒时为0，此时速度达到最大在之后4秒做减速运动。在轨迹规划过程中角速度与加速度曲线没有突然变化，表示该机械臂在运行过程中相当平稳没有出现剧烈震颤，同时说明该机械臂设计较为合理。

特殊的，关节4个变量随时间没有明显变化。但是并不意味着该关节在实际工作中丧失功能性，在其余逆解超出关节变量范围时可通过关节4的变化实现功能。

3.2 笛卡尔空间轨迹规划

依据关节空间轨迹规划的起始点与终点得到的机械臂的末端执行器的位姿分别为T1=transl(0.2，0.2，0.2)，T2=transl(0.2，-0.1，0.1)以T1与T2为始末状态调用ctraj函数对其进行位移轨迹空间规划，得到图6和图7。

图6 x-y平面的笛卡尔位移轨迹图

图7 笛卡尔空间轨迹图

4 工作空间

工作空间是衡量机器臂性能的重要指标，工作空间的大小决定了机械臂逆解的可行性，是末端执行器所有能够达到的目标点的合集。

目前求解工作空间的方法较多，但蒙特卡洛作为优秀的一种数值方法广泛求解于随机事件的问题。本文采用此方法求解五自由度机器人的工作空间。

通过导入上文建立的机械臂模型，设置各个关节的关节限制角度与计算点数n=5000，结合正运动学仿真函数，绘制机械臂在XYZ坐标空间的工作空间点云图。如图8～图11所示，为在基坐标下工作空间以及在各直角平面的投影。

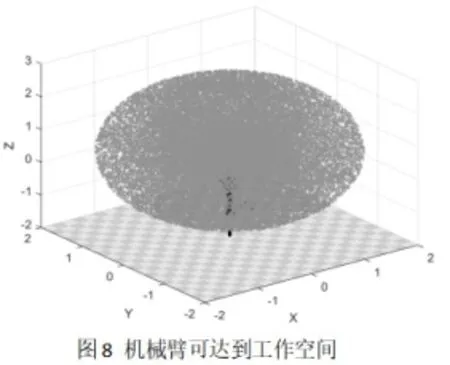
图8 机械臂可达到工作空间

图9 工作空间XOY平面的投影

图10 工作空间在XOZ平面的投影

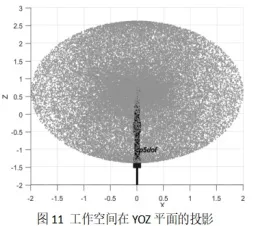
图11 工作空间YOZ平面的投影

在仿真实验中我们可以通过改变计算点数n的大小获得更加接近真实工作空间的仿真数据。实验发现，当计算点数n分别取1000，5000和9000时获得的工作空间有所不同，但是当n值取越大越符合机械臂的真实工作空间。

5 结语

本文基于设计的一种家庭服务类机器人，舍弃传统类人三自由度手臂的设计，采用五自由度机械臂的设计。通过在SolidWorks中建模设计构建了5自由度机械臂的模型。运用D-H法建立了机械臂的数学模型，得到相关几何参数后分析计算了其正逆运动的算法。通过MATLAB软件仿真分析了其正逆运动的正确性，在可允许的工作空间内，对五自由度手臂的关节空间进行分析，确保关节在运动过程中的平滑稳定并给出了末端执行器的位移轨迹，验证建立的机器人手臂模型设计的合理性。相比于三自由度机械臂，五自由度手臂在任务执行过程中，关节角变化更小，所需活动空间更小，同时能达到的工作空间更优于三自由度，为之后机器人手臂的控制提供现实基础。