小区域单镜头无人机倾斜摄影航线布设及建模精度研究

蓝贵文, 李壁宏, 凌聪聪, 何广焕

(1.桂林理工大学 测绘地理信息学院,广西 桂林 541004; 2.广西空间信息与测绘重点实验室,广西 桂林 541004)

0 引 言

近年来,无人机倾斜摄影测量是城市三维重建的重要手段之一[1-4]。目前,为了建设智慧城市、智慧校园的需要,对于小区域的街区、校园实景三维建模需求日益提高。利用单镜头无人机对小区域范围进行多角度拍摄,对实景三维建模,具有实用性、灵活性、经济性等优点,在该领域有着巨大的应用潜力[5]。航线布设方式作为倾斜摄影的重要环节,直接影响外业影像采集的高效性及后期建模精度。因此,需要对文章提出的井字型航线、折线型航线以及对角交叉型航线的布设方式分别进行探讨。

文献[6]利用多旋翼单镜头无人机,对同一建筑物进行不同航线的规划,构建该建筑物的三维模型,并从模型的完整性和地面点位精度2个方面对不同航线建模方法进行评述;文献[7]利用消费级无人机对小区域进行倾斜影像获取及三维模型构建,根据消费级无人机的特点设计其航线,并对三维模型进行精度分析;文献[8]采用四旋翼无人机航拍复杂地形,构建地面三维模型,获取地物点坐标并进行精度评定,探讨三维模型在复杂地形辅助测量的适用性;文献[9]针对传统的无人机航线规划大都只考虑垂直拍摄角度而不考虑倾斜拍摄角度的不足,结合滑坡地区,对比同一测区垂直摄影与倾斜摄影的结果进行分析。

在诸多的研究中,针对校园小区域的研究相对较少,本文根据前人的研究,结合校园具体情况,提出利用四旋翼消费级单镜头无人机,采用井字型航线、折线型航线、对角交叉型航线,分别采集实验区域的影像数据。利用Context Capture三维建模软件建立校园研究区三维模型,并对三维模型成果精度进行分析比较。

1 单镜头无人机三维建模关键技术

1.1 不同航线下影像采集方法

1.1.1 井字型航线影像获取方法

井字型航线如图1所示。

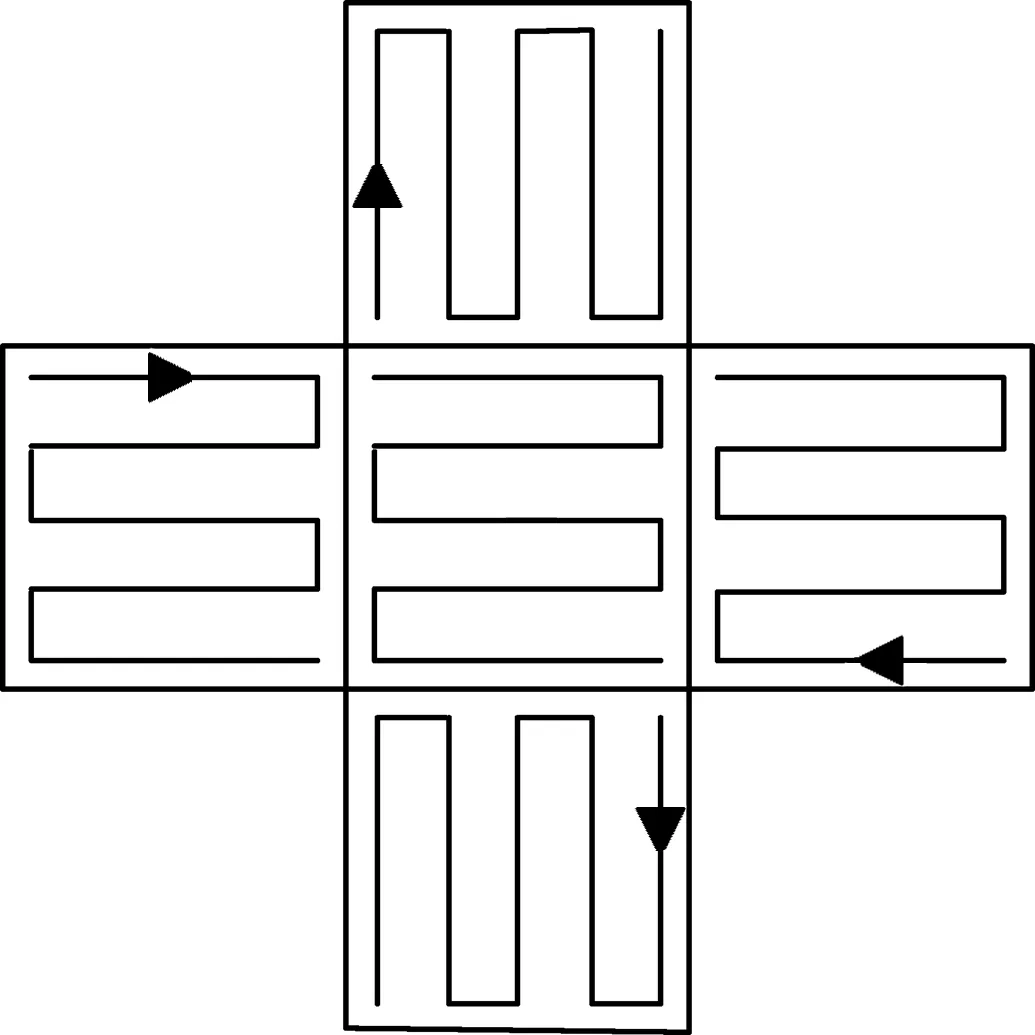
图1 井字型航线

井字型航线的核心思想是无人机飞行路径为井字型,即无人机从后视、前视、左视、右视4个角度获取地面完整的地面信息,由4个方向的航线连接而成的飞行轨迹是井字型[10]。为实现单镜头与专业五镜头获取倾斜影像的相似效果,需要地面站控制和设置镜头角度,从前、后、左、右、垂直5个角度对研究区域实现倾斜影像的采集[11]。图1中小三角形方向为无人机拍摄视角。

1.1.2 折线型航线影像获取方法

折线型航线如图2所示。其核心思想是通过分别从后视、前视、左视、右视4个视角获取倾斜影像。图2b所示为折线型航线局部放大图,其中箭头方向为无人机飞行方向,小三角形为无人机拍摄视角,航带3云台镜头角度为-90°。

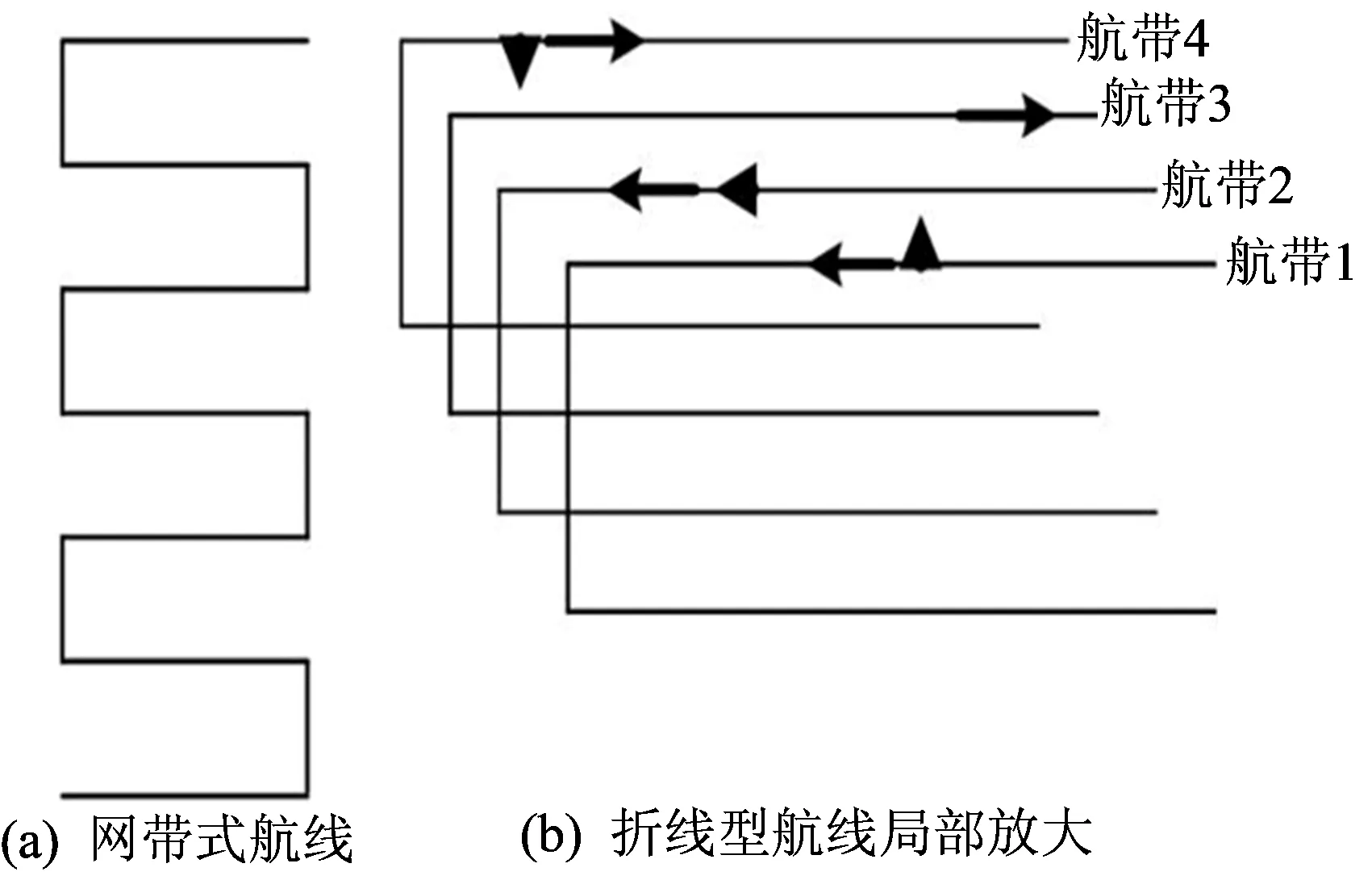
图2 折线型航线

1.1.3 对角交叉型航线影像获取方法

对角交叉型航线如图3所示,其核心思想是使2个网带式航线垂直叠加,分别从垂直、对角2个视角获取地物信息影像数据。采用对角交叉型航线,可获取研究区地物4个侧面方向的倾斜影像[12]。图3b中小三角形方向为无人机拍摄视角。

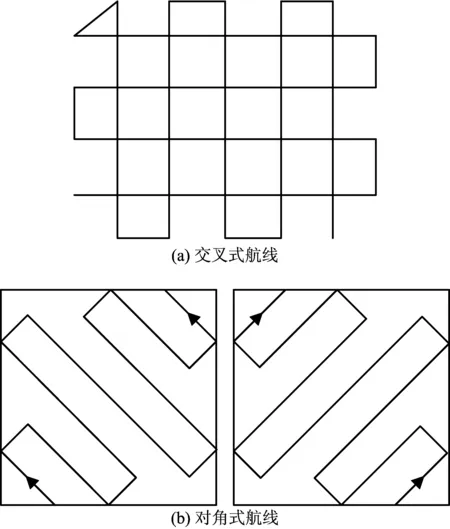
图3 对角交叉型航线

1.2 精度验证方法

为了评定3种航线布设方式所构建三维模型的精度,本文将从模型完整性、点位平面误差、高程残差和平面中误差进行验证。

利用检核点三维坐标(Xi,Yi,Zi)与模型三维坐标(Xj,Yj,Zj),进行计算得到三维坐标值残差(ΔX,ΔY,ΔZ),其数学表达式为:

(1)

根据X、Y、Z3个方向的坐标值残差,由点位平面误差公式分别计算得到3种三维模型检核点的点位平面误差,其数学表达式为:

(2)

其中,n为检核点的数量。

根据X、Y、Z3个方向的坐标值残差,通过中误差公式分别计算得到3种三维模型X、Y、Z3个坐标轴方向的中误差,其数学表达式为:

(3)

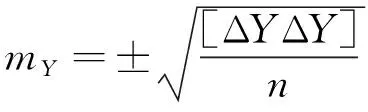
(4)

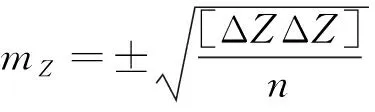
(5)

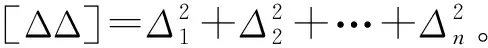
(6)

2 不同航线下三维重建实例

2.1 测区概况及像控点的布设与测量

本文选取桂林理工大学(雁山校区)的典型区域进行研究,研究区域面积约为0.19 km2。像控点的布设方式与测量精度对三维模型成果精度具有较大影响。因此,本文采用红白相间的标志作

为像控点,布设方案采用边缘均匀布设,内部少量布设的原则,故在研究区共布设8个像控点,利用网络RTK量测像控点,坐标系统为国家CGCS2000坐标系。

2.2 影像数据获取

本文实验采用大疆Phantom 4 Pro消费级单镜头无人机,搭载2.54 cm 2 000×104像素CMOS传感器捕捉高清影像。井字型航线、折线型航线及对角交叉型航线通过DJI GS Pro地面站实现对研究区域的影像采集。为了便于不同航线建模精度的比较,对每一种航线设置相同的航向重叠度、旁向重叠度和航高,具体信息见表1所列。

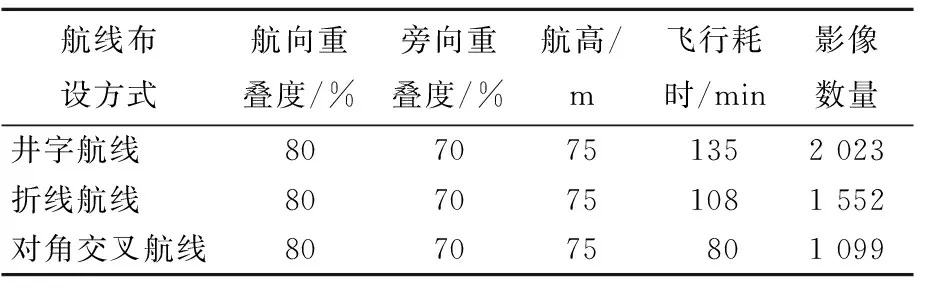
表1 不同航线下的飞行参数

3 不同航线下的三维模型对比分析

3.1 模型完整性

选取模型中具有代表性的局部区域,从模型的变形程度和模型纹理细节对比分析3种不同航线下模型的优越性。

3种航线下建筑物模型屋顶区域对比如图4所示。由图4可知,3种不同航线下模型均没有明显的变形,但纹理均有缺失。对角交叉型航线三维模型纹理缺失比较严重,建筑物顶部墙体存在较多的空洞;折线型航线三维模型也有上述情况,但空洞数量略少于对角交叉型航线;井字型航线三维模型具有较少的空洞,模型完整性最好。

图4 不同航线下建筑物模型屋顶部分对比

不同航线下建筑物模型墙面部分对比如图5所示。

由图5可知，对于建筑物墙面部分,对角交叉型航线三维模型存在比较明显的变形和纹理缺失;而折线型航线和井字型航线三维模型完整性表现较好且变形程度较小。

图5 不同航线下建筑物模型墙面部分对比

3.2 检核点精度

在三维模型中选取10个检核点,以RTK实测值作为坐标真值,求出3组模型检核点的各项误差。高程残差结果如图6所示，点位平面误差结果见表2所列。

3种三维模型的X坐标轴方向、Y坐标轴方向中误差、平面中误差、高程中误差结果见表3所列。

图6 不同航线下三维模型检核点高程残差曲线对比

表2 不同航线下三维模型点位平面误差统计 单位:m

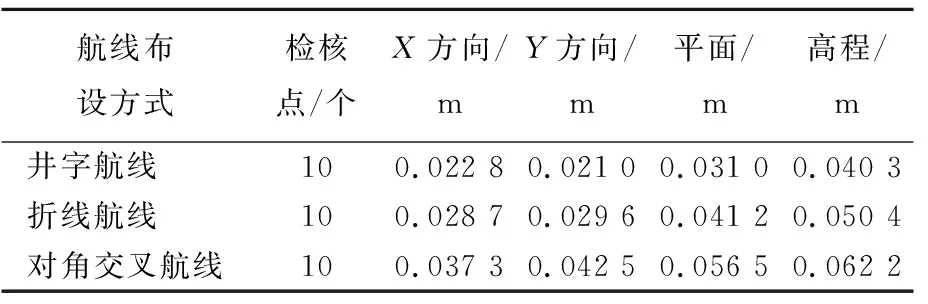
表3 不同航线下三维模型中误差比较

由表2、表3、图6可知,在3种航线布设方式所构建的三维模型精度中,井字型航线三维模型点位平面误差最大为0.039 3 m,高程中误差最大为0.046 1 m;折线型航线三维模型点位平面误差最大为0.046 2 m,高程中误差最大为0.069 4 m; 对角交叉型航线三维模型点位平面误差最大为0.071 0 m,高程中误差最大为0.075 1 m。对角交叉型航线模型的点位平面误差平均值、平面中误差、高程残差平均值、高程中误差均比井字型航线模型及折线型航线模型略低,但精度完全满足规范中规定的Ⅰ级产品要求。井字型航线和折线型航线布设方式有利于提高三维模型成果的平面与高程精度,但存在外业航拍效率低、飞行成本较高、数据量大、数据处理时间久等问题。

4 结 论

本文面向校园、街区等小区域范围,利用消费级单镜头无人机,研究了不同航线布设方式对三维模型精度的影响,分别采用井字型航线、折线型航线、对角交叉型航线对校园典型区域进行影像采集与数据处理,并对不同的航线布设方式所构建的三维模型的平面及高程精度进行了比较分析。3种航线布设方式所构建的三维模型精度均满足《三维地理信息模型数据产品规范》(CH/T 9015—2012)中Ⅰ级产品的要求。