基于分数阶模型的直流降压变换器自抗扰控制
张 杰,李 娟,王书旺,崔荣华,李生权(扬州大学电气与能源动力工程学院,江苏 扬州 225127)
1 引言
作为DC-DC变换器的基本拓扑结构,Buck变换器广泛应用于工程实际,如电动汽车和航空航天工程。由于电力电子转换器的开关操作以及混沌和分叉等现象的存在,Buck变换器也是一个时变非线性系统,同时由于存在的建模误差和输出端负载突变等干扰也会对Buck变换器的高效和精确控制性能提出严峻挑战[1,2]。因此,Buck变换器的建模和分析是设计变换器以满足实际需求的重要步骤,即模型的精度对最终设计的性能有至关重要的影响。到目前为止,许多学者针对Buck变换器,提出了一些较好的建模方法,并对其动态行为进行准确分析[3]。20世纪70年代,Middlebrook和Cuk提出了状态空间平均法,对开关变换器的建模具有重大意义[4]。随着开关变换器向高频化和高效率发展,离散时间法、等效小参量法等高精度的建模方法也被提出[5],提高了开关变换器的扩展性。
分数阶微积分起源于非整数阶导数和积分的推广,近几年在建模和控制领域受到越来越多的关注。文献[6]对永磁同步电机分数阶建模,较整数阶模型更精确描述了对象的本质。文献[7]基于伯德思想的分数阶控制策略可以保证对慢变干扰和高频噪声有足够的抑制能力,而不降低动态响应速度。其次,学者们在对实际电感和实际电容数学模型的研究中发现,利用分数阶微积分建模,能更逼近实际系统的数学模型[8]。
此外,相比传统整数阶控制器,分数阶控制器增加了更多的调参自由,因此针对系统对象可以提供更多的控制选择和更大的灵活性[9-12]。到目前为止,分数阶控制器有很多种。文献[9]中在传统PID控制器的基础上,提出了最优分数阶PID控制器的设计方法,能够同时满足频域和时域两方面的要求,达到最优跟踪性能。文献[10]提出了一种将整数阶自抗扰控制(Integer Order Active Disturbance Rejection Control,IOADRC)用于分数阶系统的整数阶控制方案,将分数阶动力学视为干扰并主动抑制它,利用自抗扰控制实现期望响应。文献[11]提出利用降阶扩张状态观测器抵消负载和输入端电压变化对控制系统的影响,有效改善控制对象的动态性能。文献[12]针对Boost变换器分数阶模型,搭建分数阶PID控制器构成全分数阶化的系统,在快速性以及稳定性方面具有较好的性能。
本文选取状态空间平均法,对Buck变换器进行分数阶建模,并与整数阶模型作比较;在此基础上,针对所提的Buck变换器分数阶模型,基于串联分数阶积分器等效的思想,提出一种分数阶自抗扰(Fractional Order Active Disturbance Rejection Control,FOADRC)设计方案,并且从理论上证明了所提控制方案的稳定性。最后,给出仿真和实验验证结果。
2 Buck变换器的分数阶数学建模与分析
2.1 Buck变换器的分数阶数学建模
实际实验中,针对元器件电感和电容的分数阶特性,在建立Buck变换器的数学模型时,采用分数阶方法,可以更好地描述系统的动态行为。分数阶微积分算子的定义如下:
(1)
式中,γ为分数阶导数和积分的阶次;δ和a为运算的上、下限,则可知分数阶器件电压电流关系式如下式所示[13]:
(2)
式中,L为电感;iL、VL分别为电感电流和电感电压;C为电容;iC为电容电流;vs为输出端两端的电压;α、β分别为电感阶次和电容阶次,并且满足条件0<α,β<1。一个典型的基于脉宽调制的Buck变换器的工作方式如图1所示,其中T为功率开关管,VD为续流二极管,Vin为输入电压,R为负载电阻。由于电感的电流和电容的电压不会突然变化,因此Buck变换器的动态数学模型可以推导如下:
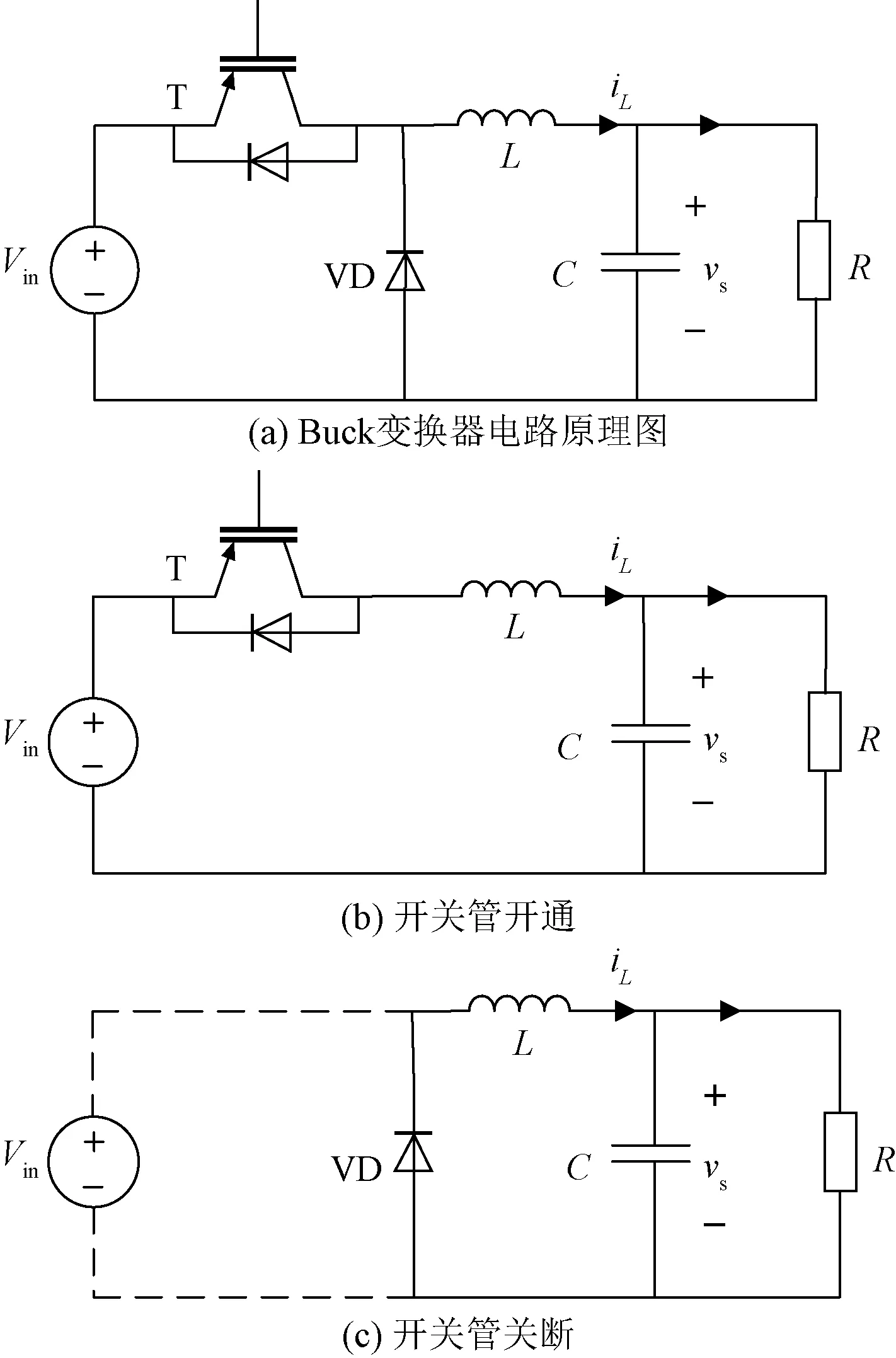
图1 Buck变换器的平均模型电路Fig.1 Average model circuit of Buck converter
当开关管开通时,电路图如图1(b)所示,数学模型如下:
(3)
当开关管关断时,电路图如图1(c)所示,数学模型如下:
(4)
由式(3)和式(4)可得系统的平均模型为:
(5)
式中,μ为占空比,μ∈[0,1]。
2.2 模型对比分析
为了验证所提方法的可行性,基于文献[14]所提的改进型Oustaloup滤波器,分别搭建Buck变换器的分数阶和整数阶数学模型,在Matlab/Simulink软件中进行仿真分析。在分数阶微积分算法中,拟合频率段为(1×10-6,1×106),滤波器阶数为5阶;电路中元器件的参数设置:电容C为4.7×10-6F,电感L为0.01 H,电阻R为250 Ω,输入电压Vin为10 V,占空比μ为0.5。其中,根据文献[8]的链式近似法,对不同阶次进行比较,最终选取分数阶数学模型电感电容的阶次为α=β=0.8,整数阶数学模型电感电容的阶次为α=β=1。
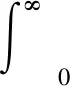

图2 两种数学模型和实际空载电路的响应曲线Fig.2 Response curves of two mathematical models and actual no-load circuits
其中,实际空载电路与分数阶数学模型输出电压的绝对误差积分为IAEf=2.7×10-4,与整数阶数学模型输出电压的绝对误差积分为IAEi=4.3×10-4,IAEf 根据文献[15]选取传统的整数阶自抗扰控制器,令x1=vs,x2=Dαx1代入式(5),将模型扩张为: (6) 式中,R0、Vin0分别为R和Vin的标称值;d为新的状态x3,即为总干扰。假设d为有界干扰,则状态方程可被表示为: (7) (8) (9) u0i=kip(vr-y)-kidξ2 (10) 式中,vr为系统输出参考值;kip和kid为增益系数。 针对上述分数阶模型,提出带有分数阶扩张状态观测器(Fractional Order Extended State Observer,FOESO)的FOADRC[17],其结构如图3所示。 图3 分数阶自抗扰控制结构框图Fig.3 Block diagram of fractional order active disturbance rejection control system 在分数阶思想上,由式(7)得D2αy=D2αx1=buf+d,其中总体控制量uf=u。针对上述变换器模型,设计对应的FOESO为: (11) 式中,z1、z2、z3分别为x1、x2、x3的估计值,结构如图3所示,整体结构的控制器设计为: (12) 将uf代入FOESO中,产生串联分数阶积分器形式D2αy≈u0f,u0f为等效控制率,由此可见系统的相位大于-180°,是稳定的系统,因此采用对噪声不敏感的比例控制器Cf(s)=kfp可以稳定,kfp为增益系数,即控制率为: u0f=kfp(vr-y) (13) 利用分数阶扩张状态观测器将对象进行校正后,本节对闭环系统进行稳定性分析。 引理[18]:根据系统阶次为α的分数阶传递函数G(s),令λ=sα,则可以转换为关于λ的整数阶传递函数G(λ),那么G(s)稳定的条件是当且仅当λ的所有极点pi均满足: (14) 式中,arg(z)为复变量z的幅角。 经过推导,分数阶自抗扰控制系统可以转化为如图4所示的二自由度控制结构,其中,w为外部干扰,Gp(s)为被控对象。由图4可知,Gp(s)、等效内环控制器Gc(s)、等效前置滤波器H(s)的表达式分别为: 图4 控制结构框图Fig.4 Control structure block diagram (15) (16) (17) 式中,a1、a2为系统模型参数,于是系统的闭环传递函数为: (18) 令λ=sα,得到: (19) 于是式(19)的特征方程为: (20) 根据引理,选择合适的控制器参数使得式(20)满足|arg(pi)|>απ/2,那么闭环系统就是有界输入有界输出稳定的,稳定区域如图5所示。 图5 稳定区域示意图Fig.5 Stable region diagram 在本节中,通过数值仿真和实验,将FOADRC与IOADRC的闭环控制性能进行比较,来验证所提控制方法的优越性。由于不同的应用场景对Buck变换器输出电压有不同的性能指标要求,为提高可参考性,综合考虑开关频率、输出电压纹波等因素,本次将选取两类参数不同的DC-DC Buck变换器,系统参数设置见表1。 表1 Buck变换器的电路参数Tab.1 Buck converter circuit parameters 首先,根据式(6),得出Buck变换器分数阶模型,在Matlab/Simulink环境中进行仿真,将分数阶自抗扰控制与整数阶自抗扰控制进行对比。在使系统具有相似动态响应速度的参数设定前提下,来比较两种控制方法的抗干扰性。FOADRC控制器中的参数选择为kfp=105,ω0=600,α=0.8,IOADRC控制器中的参数选择为kip=450,kid=20,ω0=1 000。 在仿真中,首先以第一类变换器为对象,得到负载实验下的输出响应曲线如图6所示。在3.5 s时,负载电阻从250 Ω变为200 Ω,IOADRC的输出电压变为4.65 V,变化幅度为7%,而FOADRC的输出电压变为4.75 V,变化幅度为5%;在6 s负载电阻变为250 Ω,IOADRC的输出电压变为5.4 V,变化幅度8%,而FOADRC的输出电压变为5.26 V,变化幅度为5.2%。可以看出,当发生干扰时,分数阶自抗扰控制与整数阶自抗扰控制都具有好的收敛速度,但是FOADRC能够使系统的输出电压波动更小,抗干扰能力较好。 图6 第一类中FOADRC和IOADRC在负载变化时的响应曲线Fig.6 Response curves of FOADRC and IOADRC in the first category under load changing 考虑到在实际工业中存在传感器引起的测量噪声,因此在仿真中加入随机噪声模拟实际情况,两种控制器对噪声抑制能力的比较结果如图7所示。可以看出,FOADRC与IOADRC相比,由于不含微分项,对噪声干扰不敏感从而拥有更好的鲁棒性。 图7 第一类中FOADRC和IOADRC在噪声影响下的响应曲线Fig.7 Response curves of FOADRC and IOADRC in the first category under noise influence 选取第二类变换器为对象,模拟实际噪声对其的干扰,同时在3.5 s将负载电阻由15 Ω变为10 Ω,在6 s时将负载恢复到15 Ω,FOADRC和IOADRC噪声抑制能力的比较结果如图8所示,可以发现对于不同参数的Buck变换器,FOADRC都能保证输出电压相对稳定,遇到扰动变化不激烈。 图8 第二类中FOADRC和IOADRC在噪声影响下的响应曲线Fig.8 Response curves of FOADRC and IOADRC in the second category under noise influence 为了验证所提出的FOADRC对高频噪声的抑制能力,将其与IOADRC进行比较。实验装置如图9所示。NI PCIe-6343采集实时电压信号输入到Simulink里desktop real-time环境下Analog Input模块里,产生控制量之后由Analog Output模块经NI PCIe-6343采集卡产生实际的电压控制信号,实现Buck变换器的直流降压,其中PWM信号是通过比较控制输入与锯齿波波形产生的。 首先以第一类变换器为对象,在实际噪声干扰下,FOADRC(式(12)、式(13))与IOADRC(式(9)、式(10))的闭环响应曲线如图10所示。显然,在FOADRC作用下,系统的输出电压没有剧烈的波动,控制量也更加平稳,说明对高频噪声有良好的抑制能力;为了进一步验证FOADRC的抗干扰能力,将负载电阻在4.3 s从250 Ω变为200 Ω,在7.8 s又变为250 Ω,可以发现FOADRC相较于IOADRC输出电压的变化幅度分别减小了7.8%和6.4%,具有较好的鲁棒性。 图10 实际第一类电路中FOADRC和IOADRC的响应曲线Fig.10 Response curves of FOADRC and IOADRC in actual first type circuit 将第二类变换器作为对象,在实际噪声下,在4.9 s将负载电阻由15 Ω变为10 Ω,在8.9 s时将负载恢复到15 Ω,FOADRC与IOADRC的闭环响应曲线如图11所示。对比之下,FOADRC相较于IOADRC可以使用波动更小的控制量实现稳态输出。 图11 实际第二类电路中FOADRC和IOADRC的响应曲线Fig.11 Response curves of FOADRC and IOADRC in actual second type circuit 本文基于分数阶微分建模和控制理论,构建了Buck变换器分数阶模型,并设计分数阶自抗扰控制策略。首先Buck电路的分数阶模型相较于整数阶模型更加契合实际电路的工作状态;其次通过仿真与实验结果,发现分数阶自抗扰控制器利用波动较小的控制量获得比整数阶自抗扰控制器更好的电压跟踪性能与噪声抑制能力。3 控制器设计
3.1 整数阶自抗扰控制器的设计


3.2 分数阶自抗扰控制器的设计
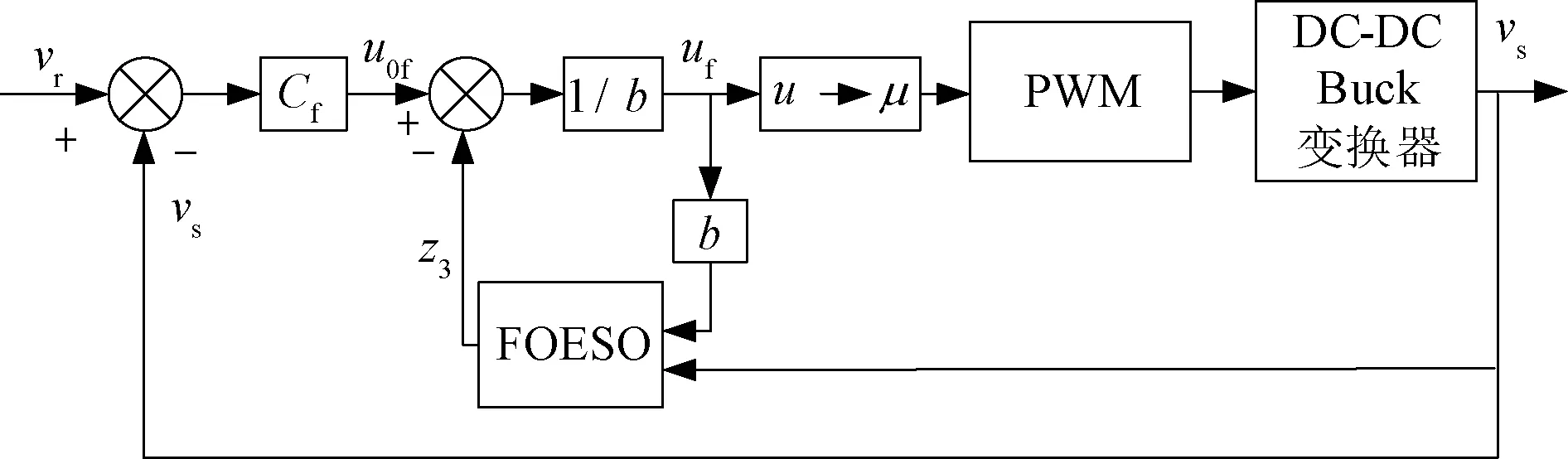
3.3 稳定性分析


4 系统验证

4.1 数值仿真
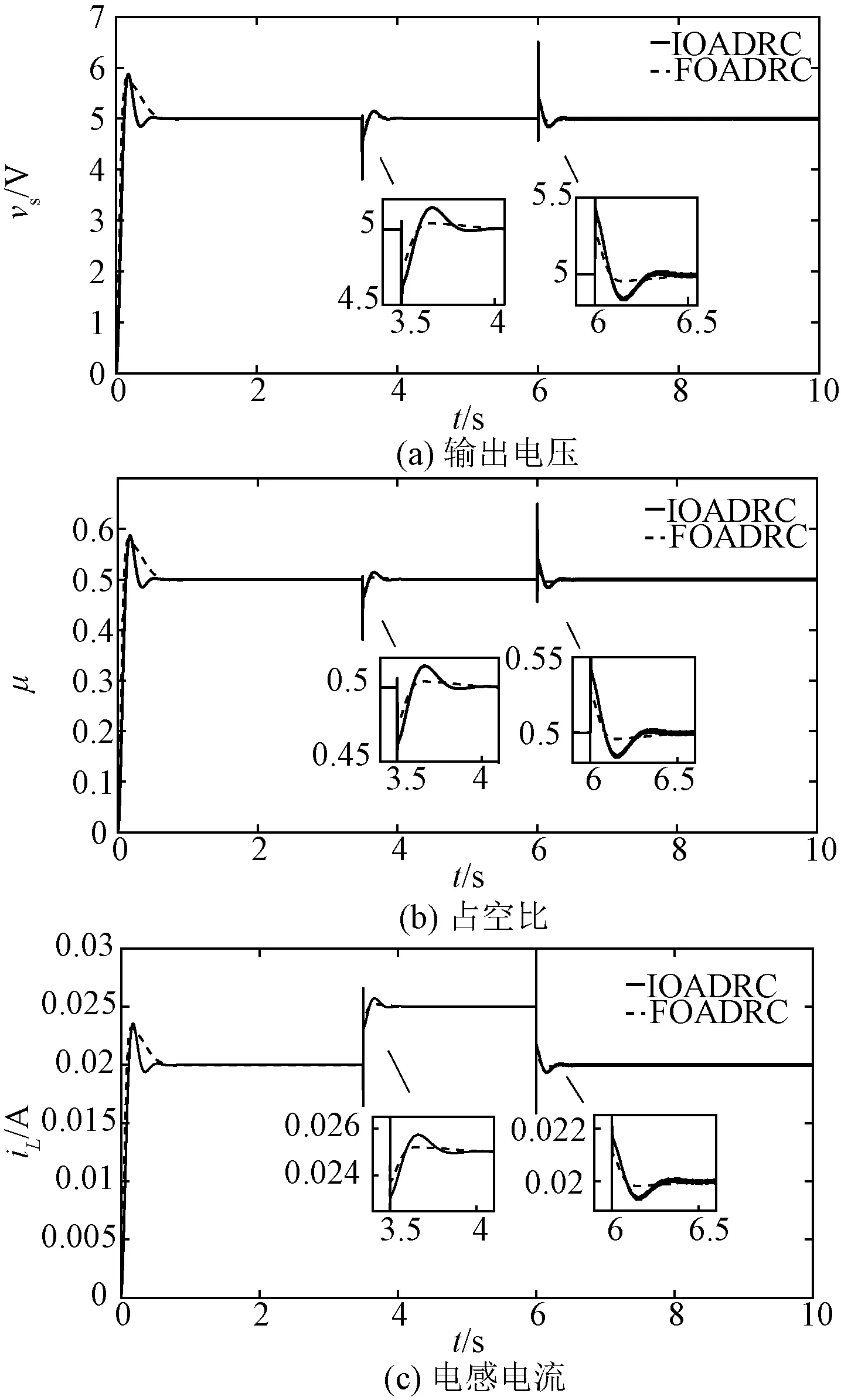
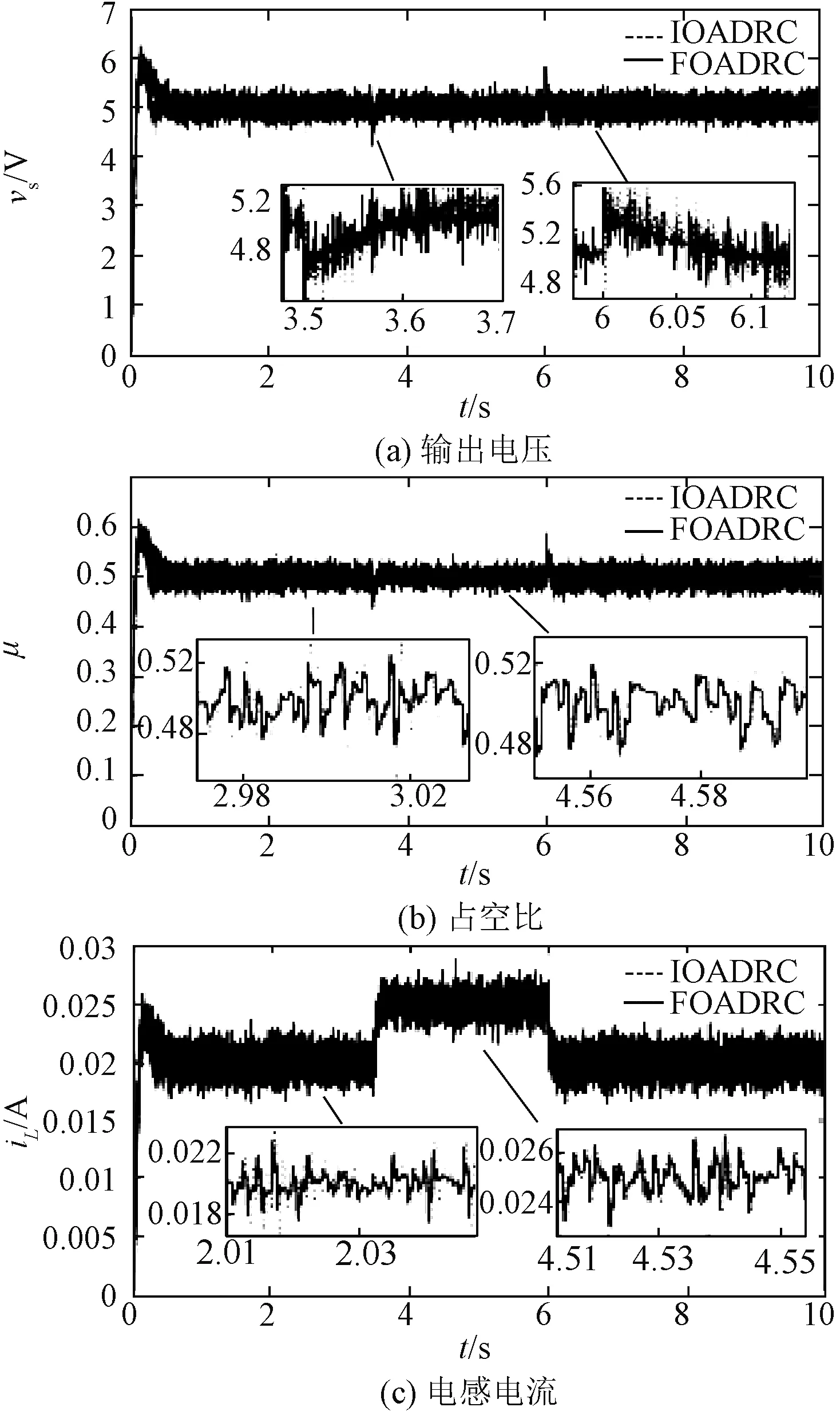

4.2 实验结果

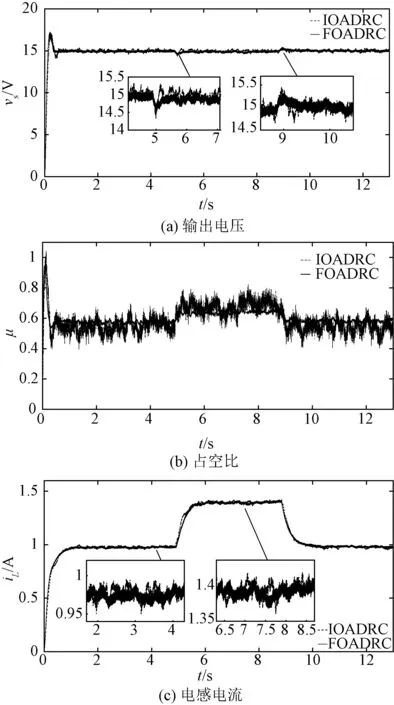
5 结论

