两道高考题的高等数学背景和推广研究
2022-08-30 02:38辽宁省黑山县第一高级中学121400刘大鹏
中学数学研究(广东) 2022年15期
辽宁省黑山县第一高级中学(121400) 刘大鹏
一、高考题再现

经过研究, 发现这两道高考题有共同的高等数学背景,下面揭示这个背景
二、两题共同的背景——彭塞列(poncelet)闭合定理
设C1,C2是两条非退化圆锥曲线, 过C1上的点P0作C2的切线, 交C1于另一点P1, 过P1作C2的切线, 交C1于另一点P2, 如此反复, 得到C1上的系列点Pi(i=0,1,··· ,n). 若有自然数n≥3,使得Pn=P0,(即n边形P1P2···Pn与C1内接且与C2外切)则对C1上的任意一点Q0,按上述方式得到Q1,Q2,··· ,Qn,也有Qn=Q0.(即n边形Q1Q2···Qn与C1内接且与C2外切).
这个定理的证明极为复杂,高中老师很难看明白,感兴趣的读者可以上网查阅相关资料.
三、高考真题1 的推广与证明
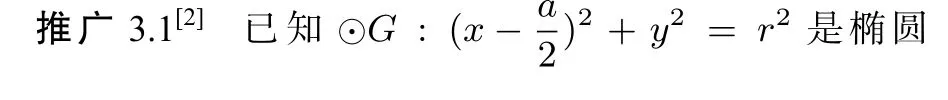



猜你喜欢
新高考·高三数学(2022年3期)2022-04-28
新世纪智能(数学备考)(2021年10期)2021-12-21
中学生数理化(高中版.高二数学)(2021年9期)2021-11-05
初中生学习指导·提升版(2020年5期)2020-09-10
高中生·天天向上(2018年1期)2018-04-14
数学学习与研究(2017年21期)2018-01-15
新高考·高一数学(2017年4期)2017-07-14
中学生数理化·高三版(2017年2期)2017-04-21
中学生数理化·高二版(2016年5期)2016-05-14
中学生数理化·中考版(2008年4期)2008-08-23

