反比例函数与三等分角的命题思路与推广

广东省佛山市三水区西南街道健力宝中学(528100) 卢健勋

命制题目是一个数学教师的基本教学技能和必备的专业能力. 数学教师加强数学命题的研究,有助提升对数学课程的理解能力、教学过程中对习题的把控能力. 以教材的例题、习题为母题进行命题改编,是各类各级考试命题的重要方法. 笔者以教材中的一则阅读材料为蓝本,通过对该阅读材料进行特殊化改造的方式来探究数学命题过程中的思路与拓展推广.

1 命题过程

1.1 试题在教材中的原型

笔者选取了北师大版九年级数学上册(2014 年6 月版)中,P156 阅读材料“反比例函数图象与三等分角”为蓝本,原材料如下:

我们知道,利用尺规可以平分任意一个角,从而可以把一个角四等分、八等分……那么,能否用尺规三等分一个任意角呢? 公元前5 世纪, 古希腊的学者们就提出了这个问题. 为了解决这个问题,数学家们花费了大量的时间和精力.直到1837 年,数学家才证明了”三等分任意角”是不能用尺规完成的. 在研究这个问题的过程中, 希腊数学家帕普斯(Pappus,约300-350)给出了一种方法,这种方法用今天的方式表示如下图所示. 你可以按以下步骤尝试做一做:

(1)建立平面直角坐标系,将已知锐角∠AOB的顶点与原点O重合,角的一边OB与x轴正方向重合.

1.2 命题的灵感和思路

以上阅读材料,只给出了“利用反比例函数三等分角”的操作方法,但并未给出证明过程. 教材的原意应该是希望学生能在课余时间对问题进行探究并加以证明. 因此,证明过程的书写是命题过程中必须要涉及的一个考查点. 在此基础上,如何让数形结合的思想方法渗透到学生利用反比例函数、一次函数的知识、等腰三角形、矩形的性质等相关知识对题目进行证明的过程中,也是笔者在命制试题时需要思考的问题.

1.3 命题的过程

1.3.1第一稿

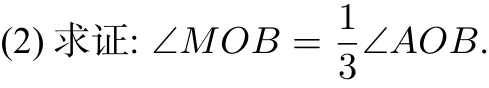
命题剖析: 本题在教材阅读材料的基础上,通过设计两个小问,分两步把利用反比例函数三等分角的证明过程进行引导,有利于降低证明的难度. 虽然学生在解题过程中要运用反比例函数、矩形等性质,但考虑到试题题干设计主要是对作图过程的叙述,因此问题设计梯度不明显,这对基础较差的学生不友好,不能较好地考察不同学生的思维深度,区分度不足,所以有了第二稿.

图1

1.3.2第二稿

如图2, 反比例函数图象的一支经过点A(1,1)、

图2

表1 ∠AOM、点A 的坐标、点C 的坐标三者之间的部分对应关系表

上表选取了部分特殊角或特殊坐标进行展示. 由上表可以看出,∠AOM是特殊角、点A、C的坐标都是特殊值这三个条件想要同时满足是很难的. 一方面是因为想要找出同时满足上述三个条件的对应关系难度比较高,第二方面是由于几何画板这个软件对角的度量和对点的坐标的表示均以保留2 位小数的近似值的形式给出,导致点的坐标中如果出现无理数,则这个点可能因保留2 位小数而被遗漏而不被发现.因此,笔者先从满足其中两个条件的对应关系入手研究.

图3

1.4 解题过程

2 命题的拓展与推广

结合笔者在命制本题过程中的思考,笔者认为本题可以向以下三个方向进行拓展与推广:

(1)∠AOM的度数、点A的坐标、点C的坐标三者之间

3 试题评析

本题属于几何知识和函数知识综合运用题,需运用一次函数、反比例函数的知识、等腰三角形的性质、矩形的性质等相关知识对题目进行求解和证明, 其题目设计也具有梯度,适合考查学生分析问题和解决问题的能力,能有效地考查学生的数学建模、直观想像等核心素养.

4 命题过程的思考

作为一线教师,我们应当注重研究教材. 研究教材,以教材中出现的例题和习题为蓝本进行二次开发,通过对条件进行弱化或强化进行有目的的改造,使之成为一类问题,让学生对这类问题产生一种“既熟悉又不同”的感觉. 这样做既能使学生迁移教材中解决问题的基本思想方法,又能引导学生关注教材、重视教材、使用教材、研究教材. 另一方面,对教师来说,以教材中出现的例题和习题为蓝本命制题目,需要教师在教学过程中加深对课堂内学生以教材为立足点生成知识过程的理解,进一步关注学生的思维深度,深入挖掘教材内涵,加强教材习题变式改编实践,提升此类题目的命题质量,使之成为提升学生核心素养的利器.

最后,在命题完成后,我们可以根据教学内容和考试难度对题目进行适当向不同方向进行拓展或延伸. 这样既能引导学生立足教材,强化基本素材积累、基本知识掌握、基本能力培养的落实,又可以考查学生不同方面的能力. 对教师来说,对命题进行适度拓展或延伸,其过程既体现了教师本人进行研究性学习的过程, 也体现了命题思路从特殊到一般,由封闭到开放的过程,在这一过程之中教师对教材的把控能力和命制题目的能力也得到了提升.