基于“问题串”设计发展学生数学建模核心素养*——以“球赛积分表问题”为例

广东省深圳实验学校(518001) 唐丽艳

《义务教育数学课程标准(2022 年版)》[1]特别强调学生综合实践素养能力的培养,由此推动育人模式的改革,并将“模型观念”列为初中数学核心素养,至此数学建模正式进入初中数学教学,数学建模具有综合性强、与其他数学核心素养联系紧密、相互交融的特点,是培养学生综合实践素养的重要途径.

课程标准指出: 学生初步感知数学建模的基本过程,从现实生活或具体情境中抽象出数学问题,用数学符号建立方程、不等式、函数等表示数学问题中的数量关系和变化规律,求出结果并讨论结果的意义[1]. 因初中学生普遍缺乏数学建模活动经验,面对实际问题往往无从下手,独立开展数学建模活动很可能就变成漫无目的的探索,因此需要教师设计逻辑连贯、循序渐进的问题串引导学生有序开展数学建模活动[2]. 笔者在2019 年代表深圳市参加广东省总工会、广东省教育厅联合主办的第二届广东省中小学青年教师教学能力大赛,在上课环节中讲授了“球赛积分表问题”,最终获得广东省初中数学决赛第一名,整个课堂以逻辑连贯、具有思维挑战性的6 个问题串,引导学生开展系列化的数学学习活动,本文将结合该案例,探讨数学建模教学中的问题串设计.

以下是教学过程设计:

1 教学内容及其地位和作用

1.1 教学内容

本节课内容是人教版数学七年级上册“第三章一元一次方程”第四节实际问题与一元一次方程—探究2 球赛积分表问题[3].

1.2 地位和作用

在学习了解一元一次方程和列简单的方程解应用题后,本节课通过对球赛积分问题的探索,让学生自主学习,合作交流,寻求问题的解决方法.

本节课内容的教学涉及代数式和一元一次方程等数学概念的理解与运用,需要掌握运用问题中的等量关系列方程的基本方法,并对运用一元一次方程解决实际问题的基本步骤有所认识,在此基础上向学生渗透方程的思想,发展学生的数学抽象、数学建模素养.

2 教学目标及解析

2.1 教学目标

(1)通过用字母、代数式和方程表示球赛积分表问题中的数量及数量关系,积累数学活动经验,发展数学抽象素养.

(2)通过用一元一次方程探究球赛积分表问题,明确列方程的基本方法,体会方程思想,发展数学建模素养.

2.2 目标解析

教学目标(1)与(2)的确定,基于数学教学内容中所蕴涵的概念与原理、思想与方法及数学素养,这表明: 探究球赛积分表不仅仅是为了解决一个具体问题,更重要的是引导学生体会用字母表示数与变量,学习用代数式和方程去表示、刻画实际问题中的数量及数量关系,并将实际问题转化为一元一次方程这个数学模型来求解,在此过程中落实“四基”“四能”,发展学生的数学建模素养.

3 教学重点、难点

3.1教学重点用一元一次方程解决球赛积分表问题,体会方程思想.

3.2教学难点利用球赛积分表问题中的等量关系列出一元一次方程,发展数学建模素养.

4 教学过程设计

导入: 观看一段2019 年男篮世界杯比赛视频.

【师生活动】

学生观看视频,教师以此引入课题.

【设计意图】

以学生熟悉的场景引入课题,激发学生的学习兴趣.

问题1 观察下列表1,你能得出比赛的积分规则吗? 即胜一场积几分? 负一场积几分?

表1 2019 年男篮世界杯小组赛A 组积分____榜

追问: 观察下列表2,你能得出比赛的积分规则吗? 即胜一场积几分? 负一场积几分?

_表2____________________某次篮球联赛积分榜

【师生活动】

教师给出问题后,让学生思考如何得出本次比赛的积分规则.

学生观察表1 波兰队的数据得出胜一场得2 分,科特迪瓦队的数据得出负一场得1 分.

教师给出表2 即教科书中的某次篮球联赛积分榜,追问学生,你能得出比赛的积分规则吗?

学生观察表2 最后一行可以得到,负一场积1 分,再利用其他任意一行的数据可以算出胜一场积2 分.

若学生无法得出积分规则,可让学生回忆表1 获取积分规则的过程,迫使学生迁移前面“先观察特殊的数据”再观察其他数据的经验.

同时,引导学生认识到,用两行不同的数据即可得出积分规则.

【设计意图】

引导学生观察表1 和表2 数据,利用两队数据得出积分规则,并认识到并没有用上表1 和表2 中的全部数据解决问题,为问题2 打下铺垫. 培养学生观察图表、分析图表及获取图表信息的能力.

问题2 只用表2 中蓝天队和雄鹰队的数据,你能得出积分规则吗?_________________________________

队名比赛场数胜场数负场数积分蓝天14 9 5 23雄鹰14 7 7 21

【师生活动】

教师给出问题后,让学生尝试解决问题,教师加以适当引导.

收集学生的解答进行点评,整理归纳学生可能的不同解法,并引导学生体会列方程的方法. 如果学生提供的解答单一,教师可启发学生探究不同的方法. 在得出积分规则后,可进一步追问学生: 若利用表2 其他两队的数据,你可以得出比赛的积分规则吗? 让学生分组探究,教师点评学生的探究结果.

追问: 给出前进队和东方队的数据可以求出积分规则吗?

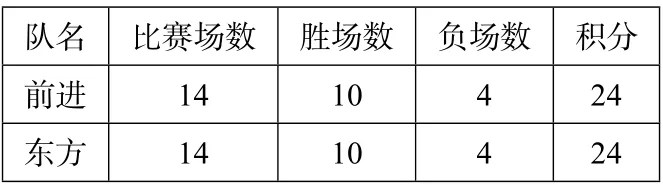
队名比赛场数胜场数负场数积分_前进14 10 4 24__东方14 10 4 24__

学生发现这两行数据一样后,引导学生认识一行数据不能得出积分规则.

【设计意图】

通过表2 信息获取积分规则,体会方程思想,明确用一元一次方程解决实际问题的基本过程,发展学生数学抽象与数学建模素养.

问题3 你能用代数式(或等式)表示某队的总积分与胜场数(或负场数)之间的数量关系吗?

【师生活动】

与学生约定用m,n分别表示胜场数和负场数.

让学生分别用含有胜场数m或负场数n的代数式表示总积分.

追问: 某队的总积分能等于17 吗? 能等于13 吗?

【设计意图】

进一步引导学生分析表格数据,学习用字母或代数式表示实际问题中的数量或数量关系;利用等量关系列出一元一次方程,并通过检验方程的解是否符合实际问题的意义,体会方程思想,明确检验是用数学模型解决实际问题的必要步骤.

问题4 某队的胜场总积分能等于它的负场总积分吗?

【师生活动】

让学生在问题3 所获结论的基础上,建立一元一次方程,并通过求解方程、检验所得解是否符合实际意义进行判断.

追问: 某队胜场总积分能等于它的负场总积分的2 倍吗? 教师在学生回答基础上进行点评.

【设计意图】

加强学生用一元一次方程解决实际问题的数学意识,积累数学活动经验,体会用数学模型解决实际问题的基本步骤,发展学生的数学抽象与数学建模素养.

想一想观察表2,你还能得到这次比赛的哪些信息呢?

引导学生思考,表格中每队的比赛场数都是14,这场比赛的赛制是什么呢? 引出双循环赛,并用具体实例介绍双循环赛的基本规则及计算比赛场数的方法.

【设计意图】

介绍篮球比赛规则,让学生了解双循环赛比赛场数的计算方法,为问题5 打下铺垫.

问题5 你能否在下面的表格中添加最少的数据,使其他小组的同学根据你给出的数据复原表2?

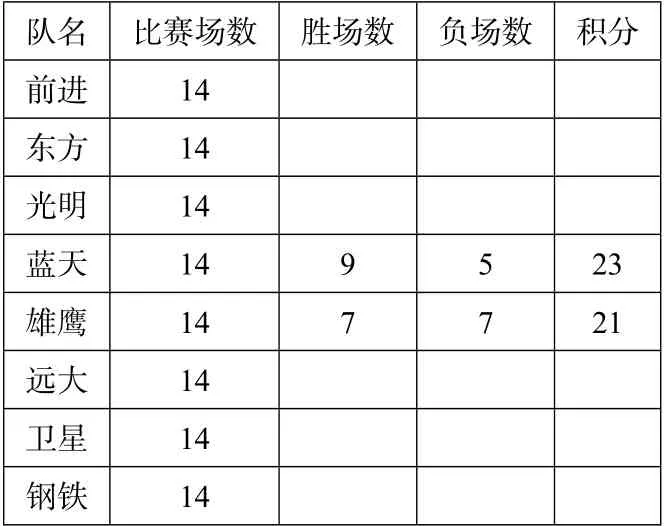
表3 某次篮球联赛积分榜

【师生活动】

让学生分组研讨,再让各组填好教师发下的表格供展示交流.

【设计意图】

帮助学生进一步提升用一元一次方程探究实际问题的能力,体会用数学模型解决实际问题的好处.

问题6 用一元一次方程解决实际问题的步骤是怎样的?

【师生活动】

教师结合已经解决的问题,引导学生归纳概括列方程的基本方法.

教师引导学生得出以下用一元一次方程解决实际问题步骤的图示:

【设计意图】

小结本节课学习内容,帮助学生进一步认识用一元一次方程解决实际问题必须经历的步骤,加深对方程思想、数学建模的认识.

5 教学反思

“用问题引导学习”是教学的一条基本准则,提高设问能力也是教师提升教学过程设计水平的关键. 区别于传统的数学活动,数学建模活动具有学生活动经验浅、入手难度大、综合要求高、思维发散强等特征,问题串的设计应该注意以下几点:

5.1 问题串设计应注重教学的整体性

完整的数学建模活动包括“问题情境——问题分析与简化——建立模型——求解模型——模型分析与检验——模型应用”等环节,问题串的设计应该将数学建模的各个要素和环节不露痕迹地体现在教学过程中,引导学生经历完整的数学建模过程,积累数学建模活动经验,形成数学建模的“一般套路”.“球赛积分表问题”中,通过设计6 个逻辑连贯、具有思维挑战性的问题串, 将数学建模的各个过程无缝连接起来,较好地体现了教学的整体性.

5.2 问题串设计应立足学生的认知水平

数学建模入手难度大、综合性强,学生缺乏相关经验,教师在问题串设计时一定要充分考虑学生的现有知识、能力水平和生活经验. 比如在抛出“球赛积分表问题”之前先观看篮球视频,可以激发学生好奇心. 在问题串设置的基础上,以互动追问的形式给予学生启发,帮助学生逐步解决问题,一步一步引导学生在解决实际问题的过程中形成一个整体框架,体现了数学知识发生、发展过程的合理性与思维过程的合理性.

5.3 问题串设计应注重开放性

数学建模具有高度开放性,已知条件不清晰,需要建模者根据情况自己提出假设,简化或者约束问题条件. 数学建模没有标准方法和标准答案,合理的方法和结论就是好的模型, 因此数学建模教学中的问题串设计要格外注重开放性,给学生自主探究留足空间. 开放性问题能够促进学生讨论交流,充分发挥学生的主体作用,激发学生的创新思维. 比如案例中的问题5 有较强的开放性,学生可以有不同的选择和方案,从实际课堂效果来看,学生的表现亮点频现,正是这些问题的抛出将课堂不断推向高潮,起到“画龙点睛”的作用.