面向配电网灵活性的电动汽车充放电控制策略研究

王梦涵，江全元

（浙江大学 电气工程学院，浙江 杭州310027）

0 引 言

随着“双碳”政策的推进，配电网中电动汽车与新能源的占比日益提升，这对配电网的灵活性提出了新的要求。 与内燃机相比，电动汽车除了具有更高的效率外，还可以将可再生能源产生的电能充电，以进一步减少温室气体的排放［1］。 电动汽车的大规模部署将对未来的电网产生重大影响。 一方面，电动汽车所需的大量能量，加上充电时间和持续时间的不确定性，对配电网电能质量、局部供电能力、安全稳定运行等都带来严重的技术和经济挑战［2-4］。 另一方面，电动汽车在一定程度上具有储能特性，它不仅可以作为负荷消耗电能，同时也可以通过电动汽车入网（Vehicle to Grid，V2G）技术［5］向电网放电，这为配电网灵活性支持提供了一个独特的机会。

目前对于电动汽车充放电控制策略的研究可以归纳为两种角度：电网侧和用户侧。 当从电网侧入手时，优化目标多为电网负荷峰谷差最小［6-7］或电网运行经济性最优［8］。 文献［7］以最小化系统总负荷水平的方差为目标建立了电动汽车参与削峰填谷的双层优化模型。 文献［8］考虑切除负荷带来的效益损失、自上级电网处购电的费用及富余可再生能源返送上网收益，以最小化电网运行成本为目标建立电动汽车充放电调度优化模型。 当从用户侧角度进行充放电控制时，优化目标多为电动汽车车主充电费用最低、充电时间最短等。 文献［9］提出以需求侧为决策主体、供需两侧协同优化的电动汽车充放电自动需求响应，为了确保用户满意度，以车辆接入电网到离开电网间的收益最大化为目标，建立了用户决策模型。 文献［10］在综合考虑用户充电时间、充电费用、等待时间、充电完成率等用户满意度指标基础上，建立了有序充电方法。

综合来看，目前对于电动汽车充放电控制的研究重点多集中在用户侧，综合考虑实时电价、用户满意度、充电成本和电池损耗等等因素，对于电网层面的关注较少，一般只考虑峰谷差或者购电成本，对于配电网灵活性的研究更是少之又少。

针对上述情况，本文从配电网灵活性出发，提出了面向配电网灵活性的电动汽车充放电双层控制策略。 首先建立了配电网灵活性指标体系和配电网灵活性评估方法，在此基础上提出了电动汽车充放电双层控制策略。 上层决策者为配电网调度中心，以最优化配电网灵活性为目标制定调度指令发布给下层；下层决策者为各电动汽车充电站，通过制定其所管辖的电动汽车的充放电计划来响应上层指令，达到和上次指令偏差最小化。最后，算例验证了本文所提电动汽车充放电控制方案能有效地提高配电网灵活性。

1 电动汽车双层调度架构

当大规模的电动汽车接入电网，如果由配电网调度中心直接对每辆电动汽车进行控制，则通信和计算的难度都很大［11］。 因此这里采用了双层控制的调度架构（见图1），上层由配电网调度机构制定调度指令，下层各电动汽车充电站响应上层计划对站内电动汽车进行灵活性控制。 具体调度方案如下：

图1 电动汽车双层调度架构

（1）日前申报机制。 为了方便上层配电网调度中心制定合理的灵活性调度决策，设定车主日前申报机制。 车主在前一天根据次日自己的出行需求申报相关信息，包括预期行驶里程、预计到达充电站时间、预期离开充电站时间和预期离开充电站的荷电状态（SOC）。 各充电站对站内的电动汽车申报信息进行统计，计算出下个时刻所能提供的最大向上、向下功率信息，并告知配电网调度中心。

（2）配电网灵活性计算。 电力系统调度中心根据各充电站上报的下个时刻所能提供的最大向上、向下功率信息，计算配电网灵活调度需求，并向下层充电站发布灵活性调度指令。

（3）电动汽车灵活性控制。 各充电站对站内电动汽车进行灵活性控制，在满足车主日常行驶需求的前提下做到尽量贴合上层调度中心的调度计划。

2 配电网灵活性评估方法

目前，已有研究提出电力系统灵活性是指电力系统在满足相应的约束条件下，面对系统中负荷的随机性和波动性能够快速响应的能力。 然而，多数研究集中于输电网，对配电网灵活性定量评估的研究较少。

本文定义配电网灵活性是指配电网在受到电动汽车负荷大规模接入条件下，能够适应负荷的较强增长和随机性，保证配电网的良好的供电质量及运行经济性的能力。

2.1 配电网灵活性指标体系

根据配电网灵活性的定义，选取如下指标建立配电网灵活性指标体系。

（1）网络损耗指标

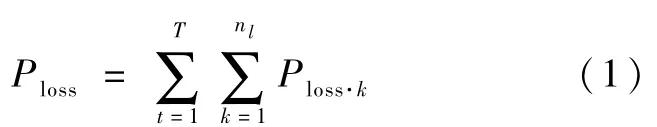
式中：Ploss·k为线路k的网损；Ploss为配网总网损；T为调度时段数。

（2） 线路裕度指标

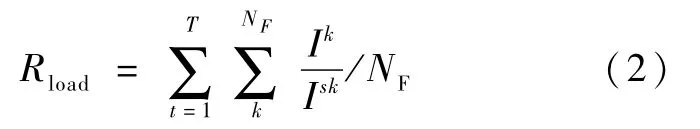
式中：Ik为线路k上的电流值；Isk线路k上允许的最大电流值；共有NF条线路。

（3） 电压偏差指标

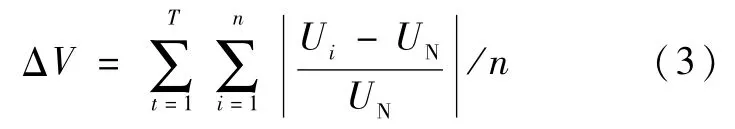
式中：ΔV表示节点电压与额定电压的电压差；UN为额定电压；Ui为节点i的电压；共有n 个节点。

（4） 馈线均衡指标

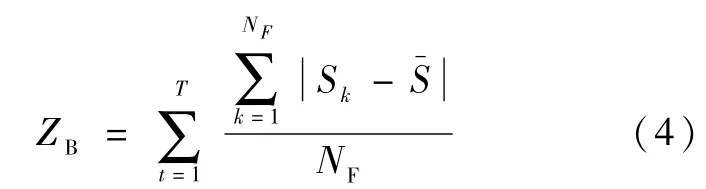
式中：Si为线路i的负载率；表示取所有线路负载率的平均值。

（5） 负荷峰谷差指标

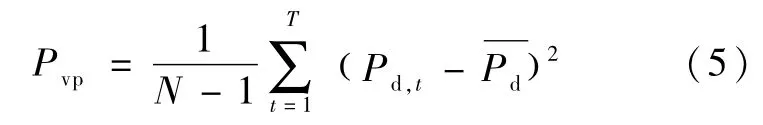
式中：Pd，t表示t时刻的负荷值；为整个时段的负荷均值。

2.2 指标权重计算

通过指标评分并赋予权重系数将所建立的配电网灵活性指标体系综合成配电网灵活性综合评分。

（1） 指标的评分

指标评分函数的归一化方式不止一种，但一般对结论不产生影响。这里参考文献［12］ 的方法进行指标评分，计算公式如下。

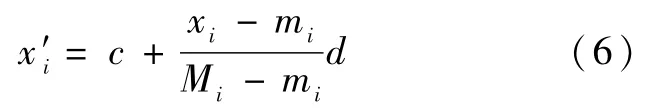
式中：x＇i为指标得分；xi为指标值；Mi、mi分别为指标的理想值和不允许值；c、d 均为常数，通常取c=60，d =40。

（2） 指标的权重

AHP层次分析法是一种定性和定量的计算权重的研究方法［13］，这里采用AHP层次分析法对于建立的指标体系进行综合。对指标层的每对指标进行比对，形成如下比较矩阵。

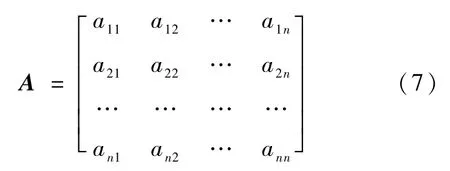
式中：aij是因素i相对因素j的重要程度。

然后根据采用AHP层次分析法计算出每个指标的权重，具体见算方法见文献［13］。

（3） 指标综合评分

基于上述方法，汇总各指标评价得分得到综合评分，计算公式为

式中：Y为综合评分值；wi为权重系数；x＇i为评价指标值。

3 电动汽车充放电控制双层优化模型

3.1 上层优化模型

本文提出的电动汽车充放电控制策略共有两层优化模型组成。上层优化的决策主体是配电网调度中心，上层配电网调度中心通过制定各个电动汽车充电站各时段的充放电策略，使得配电网灵活性值以及各电动汽车充电站实际的充放电控制结果和上层制定策略的偏差最小化，从而使配电网获得更充裕的灵活性。因此，上层优化的目标函数由两部分组成，第一部分为配电网灵活性值；第二部分为下层各电动汽车充电站实际调度结果和上层下达指令的偏差。上层优化的目标函数具体如下：

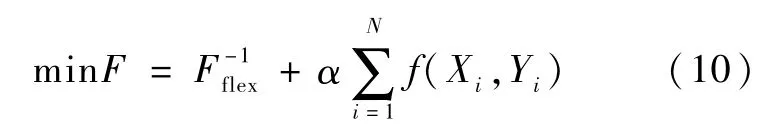
式中：T为调度周期时段数；Fflex配电网综合灵活性评分，由于经过评分计算后的配电网综合灵活性评分越高代表配电网灵活性越好，故此处取倒数；α为惩罚系数；N为配电网中电动汽车充电站数量；Xi上层配电网调度中心对第i个充电站的调度指令；Yi为第i个充电站的实际调度结果；f（Xi，Yi） 为下层第i个充电站的实际调度结果和上层配电网调度中心的指令的偏差，当上层配电网调度中心的指令和下层各充电站的调度情况产生偏差时，设置惩罚项

上层优化模型需满足的约束条件如下：

（1） 多时段潮流约束

式中：Pij、Qij为线路l（i，j） 的有功功率和无功功率；Iij表示线路l（i，j） 的电流；为节点j发电机组的有功功率和无功功率；为节点j处负荷的有功功率和无功需量；PEV，j为节点j电动汽车的充电负荷；N为此城市电网中汽车总数；rj表示节点j的电动汽车负荷占总电动汽车负荷的比例；L 为单台电动汽车的充电期望值；rij、xij为线路l（i，j） 的电阻和电抗；zij为线路l（i，j） 的阻抗；Ui为节点i电压幅值的平方。

（2） 节点电压约束

式中，Uu和Ul为节点电压的上下限。

（3） 线路电流约束

（4） 线路传输功率约束

式中：Pl、Ql为线路l（i，j） 有功功率、无功功率下限；Pu、Qu为线路l（i，j） 的有功功率、无功功率上限。

（5） 各变电站在各时段可调度容量约束

式中：Pch、Pdis分别为电动汽车平均充电和平均放电功率；nev为第i个充电站所管辖的电动汽车数量；Ii，k，t为第i个充电站内的第k辆车在t时段和电网的连接状态，Ii，k，t=1 表示该车在t时段接入电网，Ii，k，t=0 表示该车在t时段未接入电网，该值由车主在日前申报阶段的申报结果得出。

3.2 下层优化模型

下层优化的决策主体为各电动汽车充电站，各电动汽车充电站通过对站内的电动汽车充放电状态的控制，使得电动汽车实际的功率与上层配电网调度中心发布的指令的偏差达到最小。

下层优化的目标函数如下：

式中：Pev，i，k，t为第i个充电站内的第k辆车在t时段的充放电功率。

下层优化需满足如下约束：

（1） 电动汽车电池充放电约束

式中：SOCi，k，t为第i个充电站内的第k辆车在t时段结束时的电池荷电状态；Ei，k为第i个充电站内的第k辆车的电池容量；ηch和ηdis分别为电动汽车充电和放电的效率；Δt为一个时段长度；Uch，i，k，t和Udis，i，k，t为第i个充电站内的第k辆车在t时段的充放电状态标记变量，是0 -1 变量。Uch，i，k，t=1 表示该辆车在t时段处于充电状态，Uch，i，k，t=0 表示该辆车在t时段不处于充电状态；Udis，i，k，t=1 表示该辆车在t时段处于放电状态，Udis，i，k，t=0 表示该辆车在t时段不处于放电状态；式（23） 表示同一辆车同时只可能处于充电/放电一种状态，充电和放电无法同时进行。

（2） 电池安全约束

式中：SOCmin和SOCmax分别为电动汽车电池荷电状态的上下限。

（3） 日前申报约束

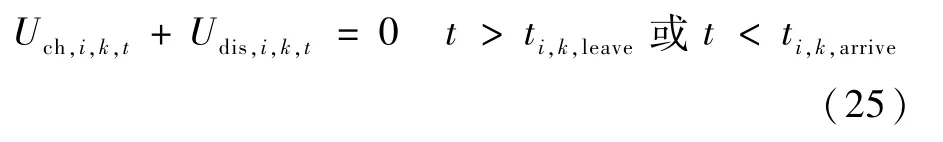
式中：ti，k，leave和t＜ti，k，arrive分别表示第i个充电站内的第k辆车离开和接入该充电站的时间，该信息由各车车主在日前向各充电站申报。在车主申报的不可调度时段，不可对该车下达调度指令。

（4） 车主行驶需求约束

式中：SOCi，k，ti，k，leave和SOCi，k，leave分 别 为 属 于 充 电站i的第k辆电动汽车在离开该充电站时的实际SOC和需要达到的SOC。

4 模型求解方法

本文所建立的双层优化模型在MATLAB中进行编写，调用Mosek 商业求解器进行求解，具体求解流程如图2 所示。

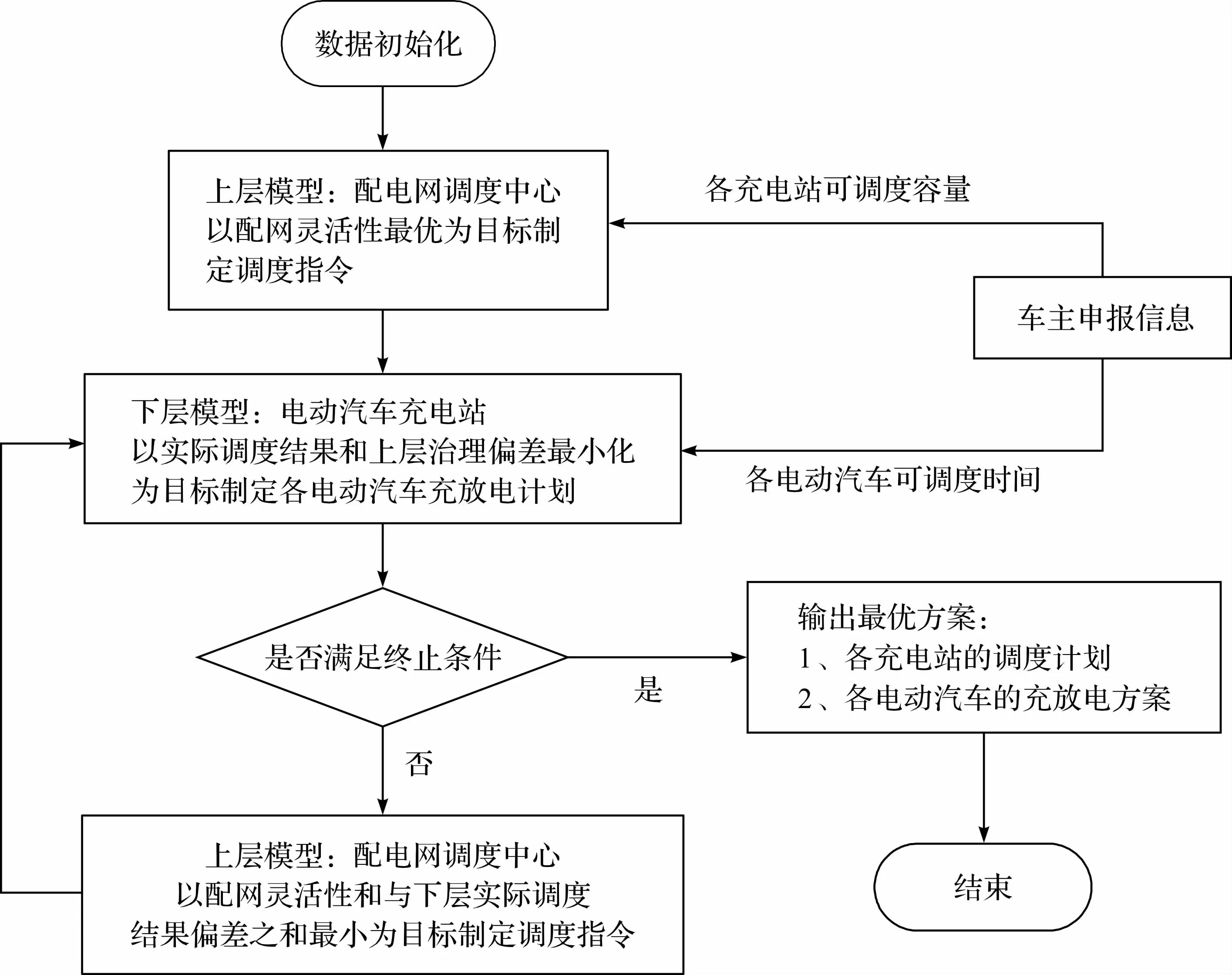
图2 电动汽车充放电控制双层优化模型求解流程

在第一次迭代时，由于不知道下层充电站调度结果，上层配电网调度中心以配电网灵活性最优为目标制定下层的各电动汽车充电站的调度指令。 下层接收到上层调度指令后，根据车主日前申报的各电动汽车可调度时间信息，以各电动汽车充电站实际调度结果和上层指令的偏差最小化为目标制定各个电动汽车的充放电计划。 当各电动汽车充电站实际调度结果和上层指令的偏差小于设定值或者迭代次数到达上限时，则视为满足终止条件，输出最优方案。 若不满足终止条件，则重新回到上层优化，以配电网灵活性值和上下层调度结果的偏差之和最小为目标制定调度指令，重新下达给下层，如此进行迭代，直至满足终止条件，输出结果。

5 算例分析

算例采用改进IEEE33 配电网节点系统，该配电网拓扑如图3 所示，额定电压为12.66 kV。节点2 安装有1 MW 的风机，节点7、19、26 安装有0.5 MW 的风机。 在节点17、31 处分别设置了一个电动汽车充电站，设定每个充电站所管辖的接受调度的电动汽车共有400 辆，电动汽车电池和充电相关参数如表1 所示。

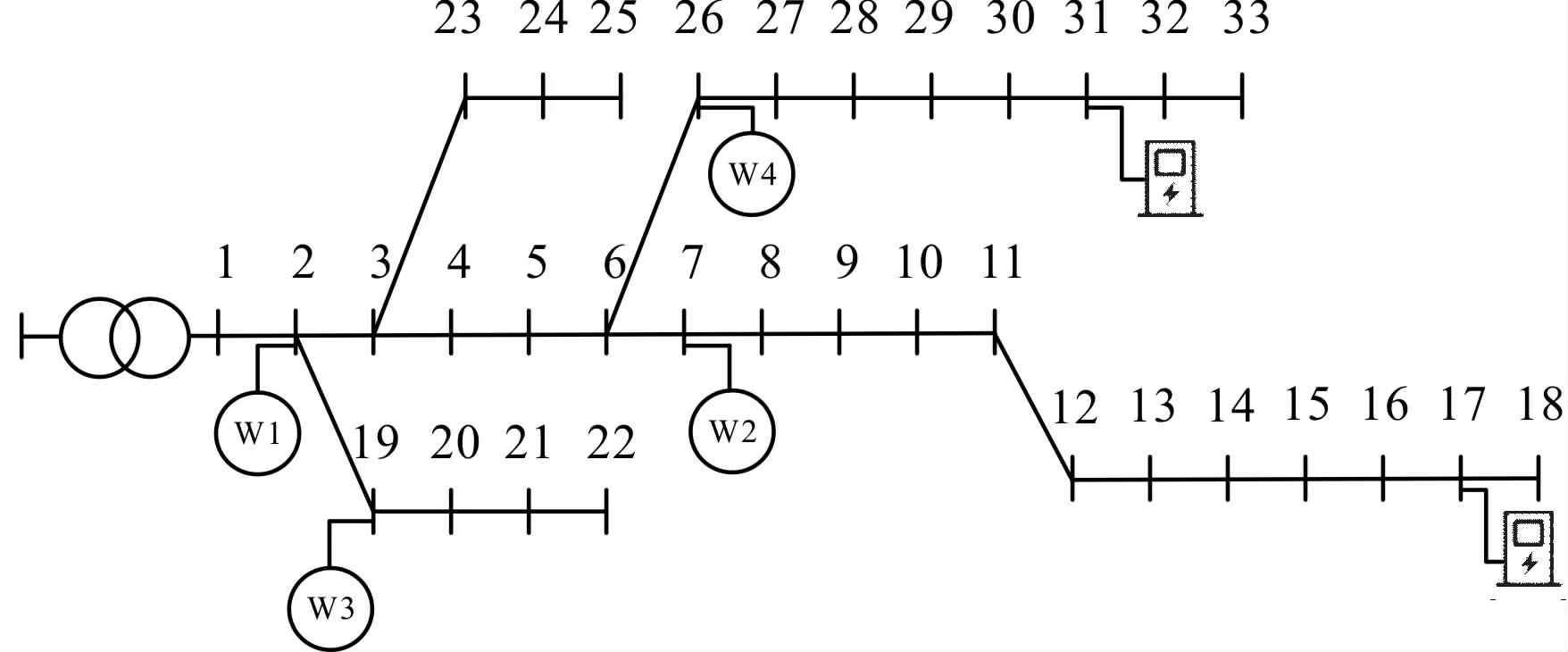
图3 改进的IEEE33 配电网

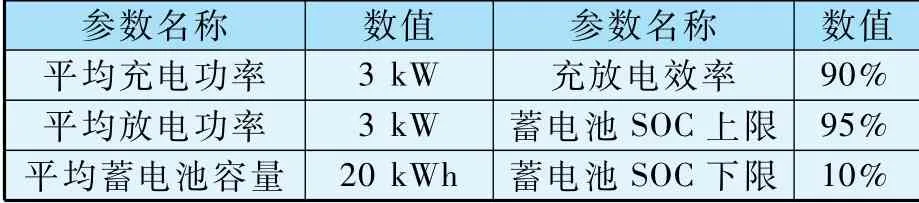
表1 电动汽车相关参数

本章的研究对象是家庭电动汽车，这类电动汽车往往由于日常出行需求，集中在夜间充电。文献［14］根据美国家庭出行调查（national household travel survey，NHTS）的结果，通过拟合得出第一次出行时刻和最后一次出行结束时刻的概率分布可近似为正态分布，而日行驶里程接近为对数正态分布函数［15］，具体的概率分布函数通过拟合后如式（27） -式（29）所示。

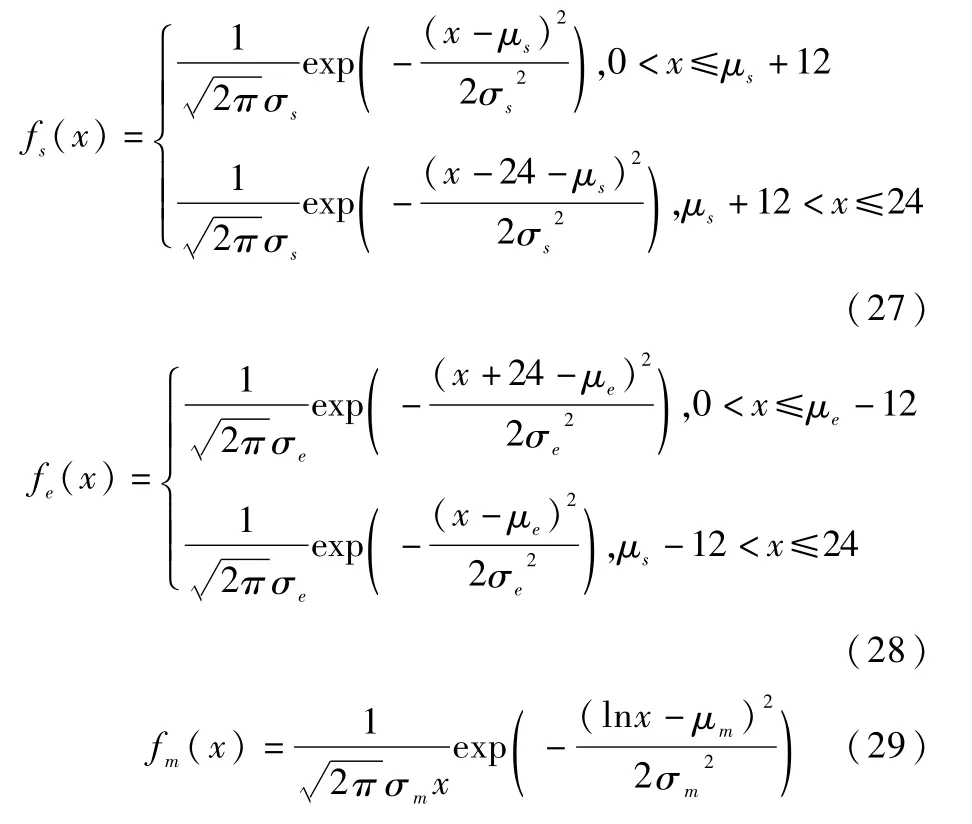
式中：fs（x）、fe（x）、fm（x）分别为第一次出行时刻、最后一次出行结束时刻和日行驶里程的概率密度函数。 μs=8.92，σs=3.24，μe=17.47，σe=341，μm=2.98，σm=1.14。

在车主的日前申报中，车主需提前一天向自己所要去的充电站上报预期行驶里程、预计到达充电站时间、预期离开充电站时间。 为了贴合实际，这里车主上报的信息将从上述概率密度函数中进行抽样，从而模拟电动汽车接入充电时刻、次日离开充电站时刻以及接入充电时的电池荷电状态。 假定车主离开时电动汽车电池荷电状态需要达到90%。

5.1 计算结果

上层调度指令和下层实际调度结果如图4 所示。 可以看到经过14 次迭代后，上下层调度曲线基本重合，结果基本一致。 其中0 -8 时中部分时段下层实际调度结果略高于上层调度指令，这是由于电动汽车出行需求造成的。 家庭电动汽车一般需要在早晨出门行驶，因此为了满足电动汽车出门行驶的荷电状态需求，需要给电动汽车在此时段进行充电，造成下层调度结果偏高。 图5 为上层调度指令和下层实际调度结果的偏差随迭代次数的变化曲线。 可以看出刚开始迭代时，由于配电网灵活性的要求（上层目标）和各电动汽车车主的行驶需求存在一定的冲突，在迭代初上下层调度结果的偏差较大。 随着迭代次数增加，上下层调度结果逐渐趋于一致，偏差渐趋于零，13 次和14 次迭代时，调度偏差变化小于10-5，迭代结束，输出计算结果，此时下层对于电动汽车充放电的控制既能满足车主需求，又能保证配电网灵活性需求。

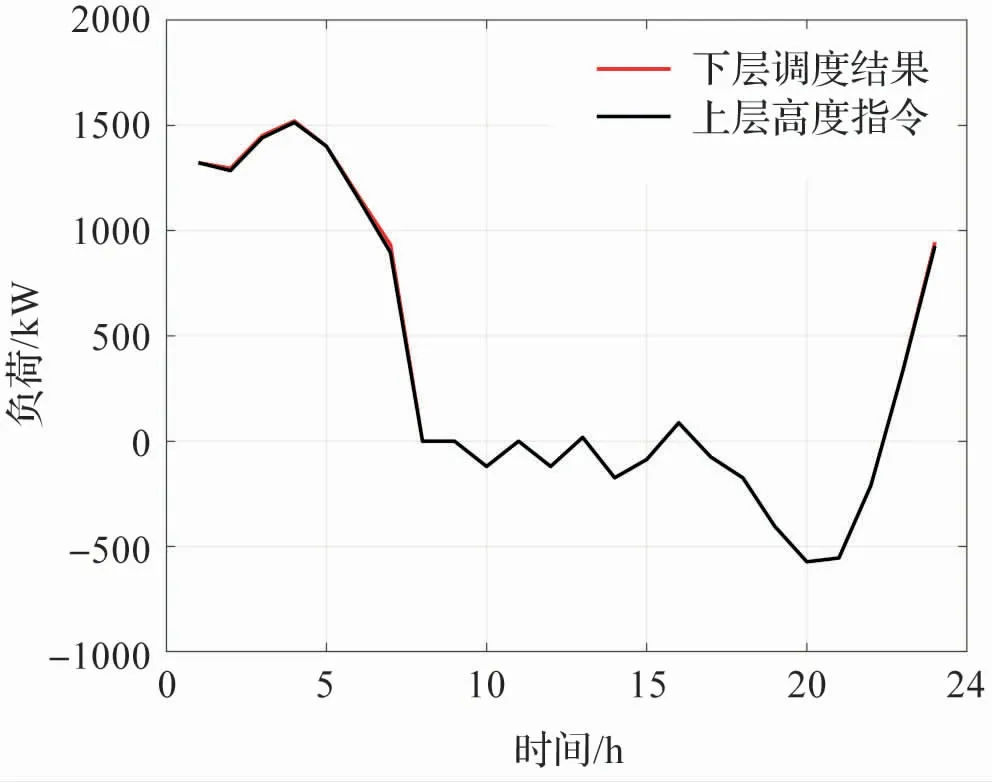
图4 上下层调度优化结果

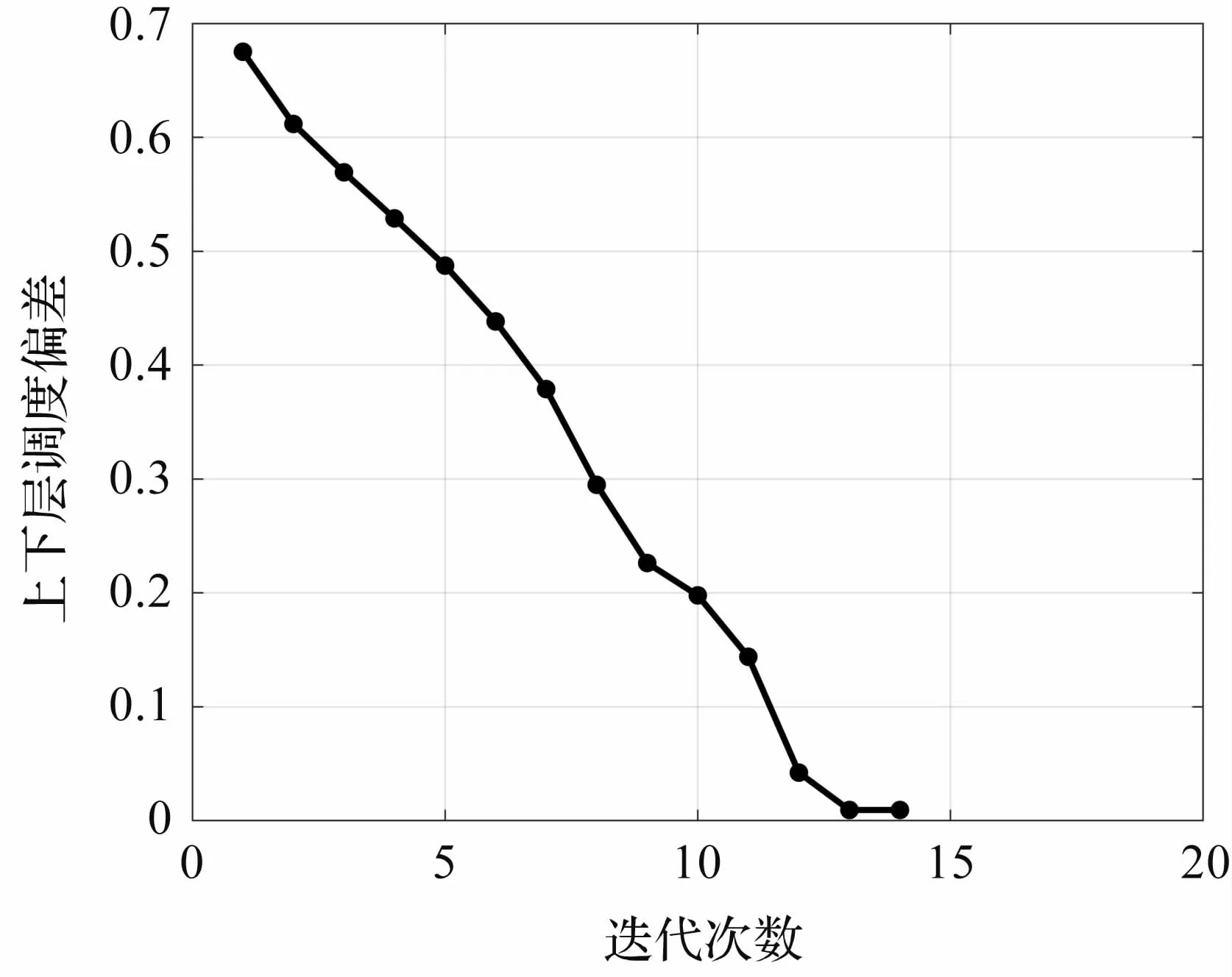
图5 上下层调度偏差

两个电动汽车充电站的实际调度结果如图6所示。 图中负荷为正值表示此充电站作为负荷向电网吸收电能，负值表示电动汽车充电站向电网输入电能。 由图可知，接入充电站的电动汽车大多在23 时到次日7 时处于充电状态，8 到22 时多为放电状态或者保持不充电也不放电，这和电网负荷峰谷时密切相关。 在本章提出的控制策略下，电动汽车在峰时放电谷时充电，降低电网负荷高峰，缓解设备压力。 其中8 到17 时电动汽车充电站充放电负荷都处于一个比较低的水平，这在一定程度上也反映了电动汽车的行驶规律，在白天电动汽车大部分都处于外出行驶状态，不接入充电站，在结束一天的行程后大部分电动汽车选择在晚上接入充电站接受充电站调度指令。

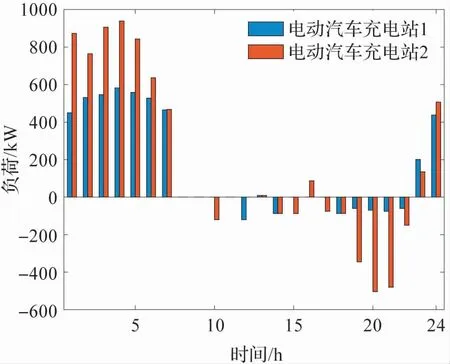
图6 各电动汽车充电站调度结果

5.2 多场景分析

为了验证本文提出的电动汽车充放电双层控制策略的有效性，计算三种场景下的配电网综合灵活性评分：

场景1：无电动汽车。 此时电网中仅考虑常规负荷，不考虑电动汽车充电负荷的接入。

场景2：电动汽车无序充电。 此时电动汽车完全按照车主自由意愿进行充电，配电网不采取任何干预手段。

场景3：电动汽车有序充放电。 此场景下采取本文所提出的电动汽车双层充放电控制策略。

三种场景下的配电网综合灵活性评分如表2所示。 在场景1 中，配电网原始状态下综合灵活性评分为70.1 分。 在800 辆电动汽车接入两所电动汽车充电站的情况下，如电动汽车完全随车主意愿自由充电，此时配电网灵活性降为60.7。可见在大规模电动汽车接入电网的情况下，如果不采取有效的控制策略，会对配电网运行的灵活性造成比较大的影响。 在本文提出的电动汽车双层优化控制策略之后，配电网综合灵活性评分上升至95.6，可以看出，在采取本文所提出的控制策略之后配电网的灵活性得到了有效的提升。

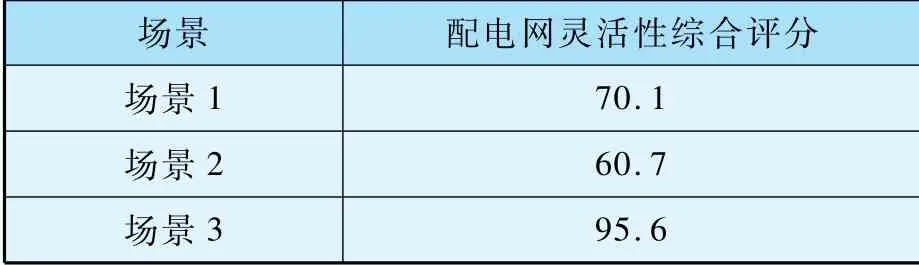
表2 配电网灵活性综合评分

图7 为三种场景下配电网的负荷曲线。 图中场景1 中负荷即配电网原始负荷值。 场景2 中电动汽车随车主意愿自由充电，可以看出电动汽车充电时段在一定程度上和配电网负荷峰值相重叠，造成了配电网负荷“峰上加峰”的情况，形成了新的峰值，这对配电网运行灵活性、可靠性、配电网设备容量都造成了一定的挑战。 在场景3中，采取了本文所提出的控制策略，可以看出配电网峰值负荷明显下降，缓解了配电设备容量压力，改善了负荷曲线。 由场景2 和场景3 对比可以看出，场景3 中把场景2 中部分峰值负荷调整到了夜间谷时，有效改善了负荷曲线，这对配电设备的运行效率也有一定的改善作用。

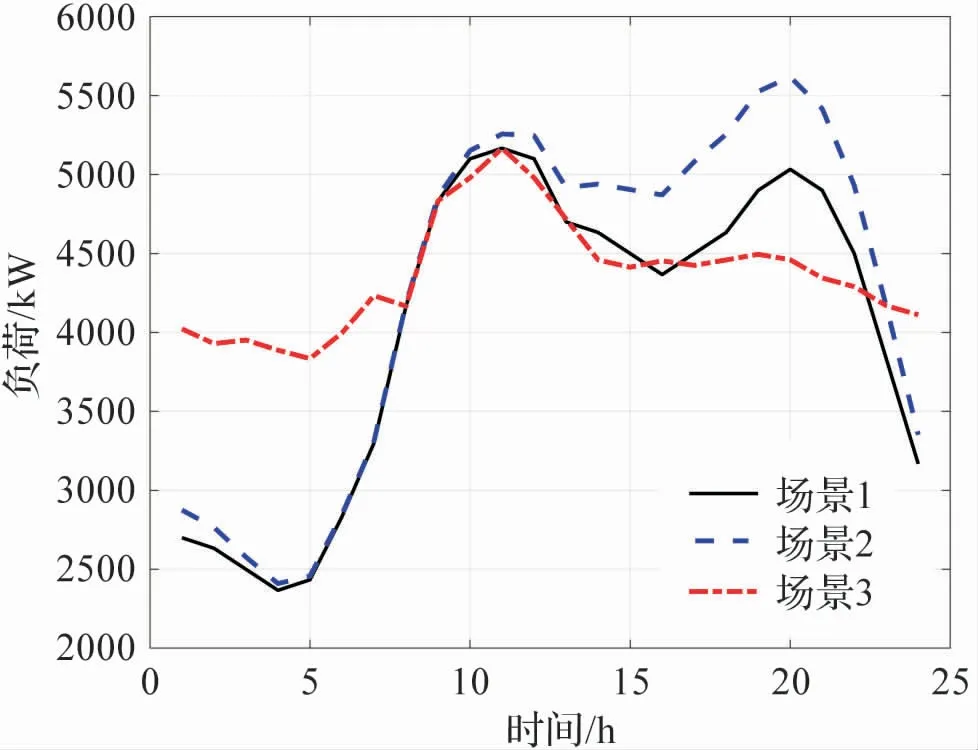
图7 三种场景下配电网负荷曲线

5.3 多场景分析

为了更直观的观察单辆电动汽车充放电情况，这里取800 辆车中两辆典的电动汽车一天的荷电状态进行观察，如图8（a）（b）所示。 表3 中给出了这两辆车主在日前申报的信息。

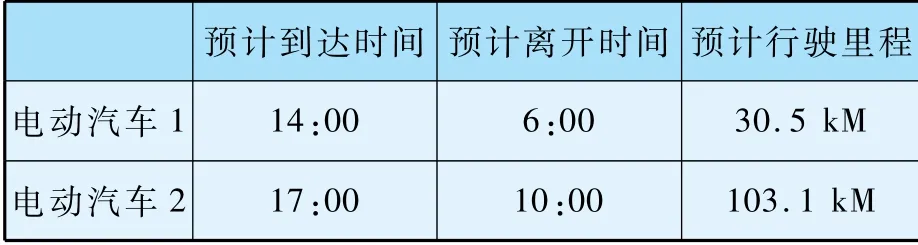
表3 车主日前申报信息

由表3 可知，电动汽车1 当日行驶里程较少，接入充电站时电池剩余电量较为充足，因此在该车刚接入充电站时根据配电网灵活性的要求安排此车对电网进行放电，在次日凌晨在根据其行驶需求进行充电。 而电动汽车2 由于其当日行驶里程较长，接入充电站时电池电量较低，无法支撑其对电网进行长时间的放电。 不过相比较于自由充电下汽车在接入充电站即时开始充电的模式，从图8（b）中可知该辆车充电时段根据电网需求整体向后延缓，这也验证了本章所提出的电动汽车双层优化控制模型的有效性。

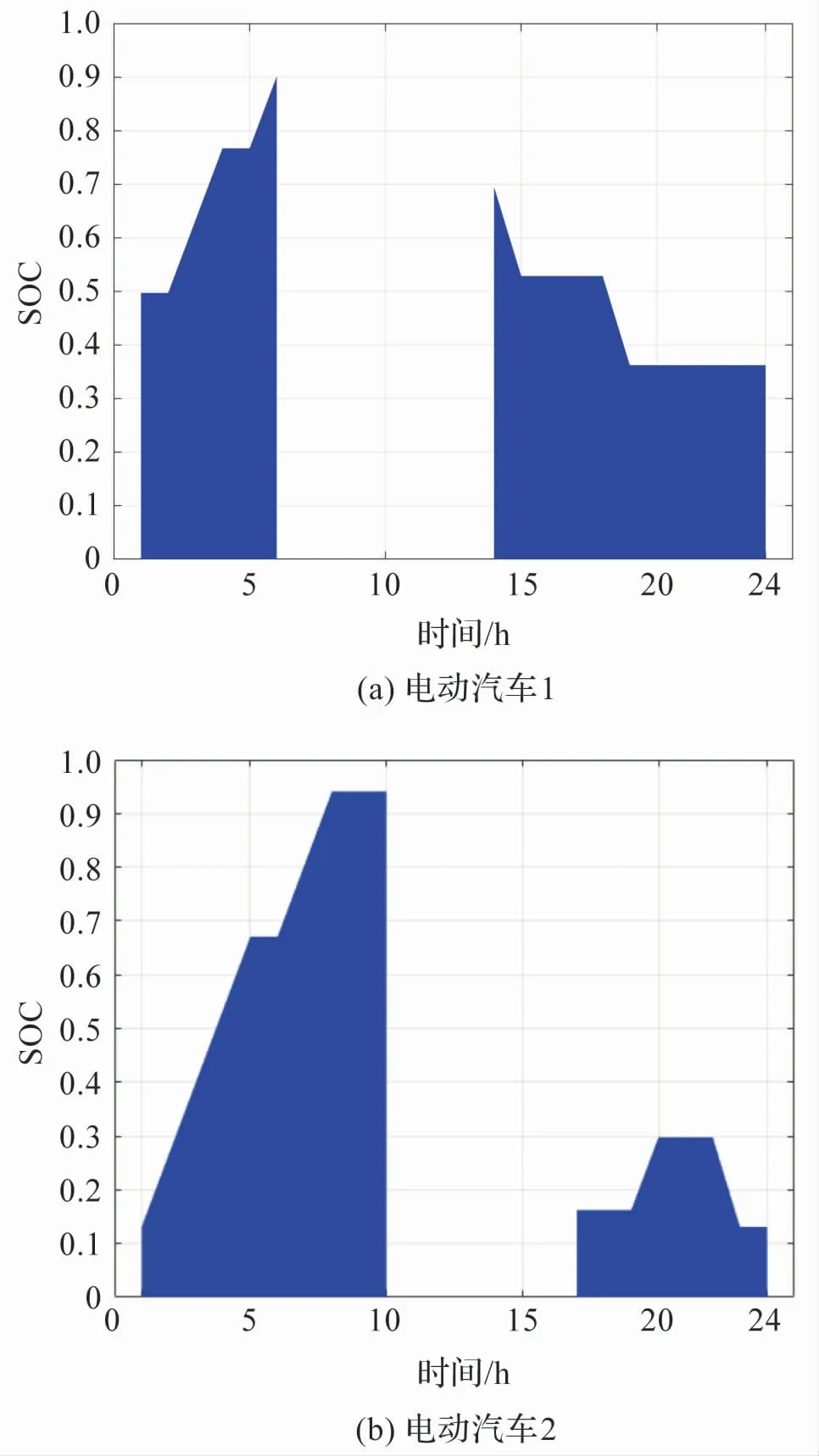
图8 电动汽车荷电状态

5 结 语

本文提出了面向配电网灵活性的电动汽车充放电双层控制策略。 首先建立了配电网灵活性指标体系和配电网灵活性评估方法，在此基础上提出了电动汽车充放电双层控制策略。 上层决策者为配电网调度中心，以最优化配电网灵活性为目标制定调度指令发布给下层；下层决策者为各电动汽车充电站，通过制定其所管辖的电动汽车的充放电计划来响应上层指令，达到和上层指令偏差最小化。 算例验证了本章所提出的电动汽车充放电双层控制策略能够有效地改善配电网的灵活性，缓解电动汽车大规模接入电网给电网造成的冲击。