砂卵石土强度变形特性综合试验及力学模型参数研究

王亚平，卢一为，张二帅，彭元诚，左永振，李浩民

(1.湖北白洋长江公路大桥有限公司，武汉 430035； 2.长江科学院 水利部岩土力学与工程重点实验室，武汉 430010； 3.中交第二公路勘察设计研究院有限公司，武汉 430052)

1 研究背景

在我国许多地区都分布有砂卵石土，随着城市建设的高速发展，越来越多的桥梁、隧道等市政交通工程建设在砂卵石土地层[1]。相比于一般的软黏土，砂卵石土具有颗粒粒径大、压缩性低、黏聚力小、自稳能力差、渗透系数大、摩擦系数大等特点[2]，在该地层上进行基坑开挖、隧道施工、结构基础变形控制时面临着巨大困难，极易引发安全事故，是岩土工程界广泛关注的问题之一。

目前针对粗粒土的单元体剪切特性[3-5]、界面剪切特性[6-8]、长期流变特性[9-11]等力学特性已经开展了大量研究，但以往研究主要针对筑坝堆石料，作为一种特殊粗粒土，砂卵石土与筑坝堆石料的物理力学性质差异较大，筑坝堆石料的研究成果无法直接应用于砂卵石土。目前针对砂卵石土的强度变形特性缺乏系统的试验研究，而基于数值仿真计算的砂卵石土地基沉降变形分析依赖于选取合适的力学模型及准确的模型参数，以上因素严重制约了砂卵石土地基上的工程建设发展，因此有必要对砂卵石土的力学特性开展系统深入的研究。

针对某典型砂卵石土地基，系统开展三轴剪切试验、界面剪切试验及三轴流变试验等，对砂卵石土的单元体剪切特性、界面剪切特性、长期流变特性等力学特性开展综合试验研究，分析试验成果选取合适的力学模型描述砂卵石土的应力-应变关系，并整理出相应的模型参数，研究成果可为砂卵石土强度变形特性研究及基础沉降变形预测提供有益借鉴。

2 试验设备及材料

2.1 试验设备

长江科学院YLSZ30-3型高压三轴仪，主要用于开展粗粒料的三轴剪切试验、流变试验等。如图1所示，该仪器主要由竖向压力和周围压力的加载、稳压、控制系统，三轴压力室，反力系统，位移、体变量测系统及数据采集系统等组成。试样尺寸为Φ300×H600 mm，最大围压为3.0 MPa，最大轴向应力为21 MPa，最大轴向行程为300 mm。

图1 YLSZ30-3型高压三轴仪Fig.1 YLSZ30-3 high-pressure triaxial instrument

长江科学院大型叠环式剪切仪，主要用于研究土料、粗粒料、结构与土的接触面、岩土与土工格栅的界面相互作用等力学特性，获得抗剪强度参数。如图2所示，试样尺寸为600 mm×600 mm×600 mm，下部剪切盒高240 mm，上部为7层叠环，每层叠环高30 mm，最大竖向荷载500 kN，水平最大荷载1 000 kN。该仪器克服了常规直剪仪中剪切面单一的缺点，使试样有可能沿最弱的剪切面发生破坏。

2.2 试验材料

试验材料取自某大型悬索桥锚锭基础下覆砂卵石土地层，地勘资料显示地层厚度约50 m，场区卵石母岩成分主要为石英砂岩，卵石粒径一般为2～15 cm不等，磨圆度一般，分选性较差，局部夹漂石，漂石粒径一般为20～40 cm，主要为中粗砾砂及黏性土充填，厚度大，富水性极强，透水性极强，为场区内主要含水层。

目前室内试验设备允许的最大粒径为60 mm，因此无法直接对原始级配砂卵石土进行试验。依据规范[12]粗粒土主要有4种缩尺方法：剔除法、等量替代法、相似级配法和混合法，其中等量替代法的优点是缩尺前后级配的粗粒含量保持不变，细粒的含量和性质保持一致，但存在大粒径缩小、粒级范围变小、均匀性增大等缺点，因此该方法适宜在超径颗粒含量≤50%的情况使用。由于骨料颗粒的含量和大小对土体的力学性质影响较大，因此本次试验采用等量替代法对超径部分颗粒进行缩尺，即用5～60 mm之间颗粒按比例等量替换粒径>60 mm颗粒，粒径<5 mm的细颗粒含量保持不变，以反映砂卵石土的真实工程力学特性。缩尺前后的级配曲线如图3所示。

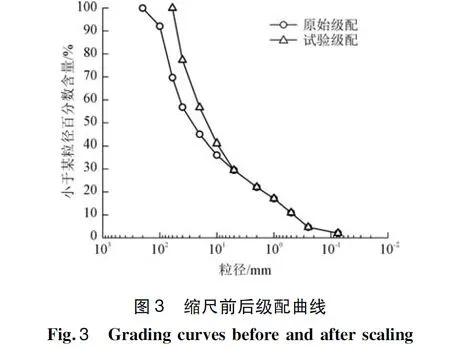
试验土样的相对密度为2.69，最大干密度为1.973 g/cm3，将95%压实度对应的干密度1.87 g/cm3作为本次试验控制密度，分别制备砂卵石土饱和样和非饱和样，试样土性指标见表1。

表1 试样土性指标

3 单元体剪切特性研究

分别对砂卵石土饱和样和非饱和样开展三轴剪切试验，根据场区砂卵石土地层厚度估算最大竖向应力约为1.0 MPa，本次三轴剪切试验的围压σ3分别取0.1、0.2、0.3、0.4 MPa，剪切速率为0.4 mm/min。试验过程中记录轴向荷载、轴向位移、排水量等，试样剪切至轴向应变εa的15%停止试验，所有试验过程均严格依照规范执行。

图4为偏应力σ1-σ3和轴向应变εa的关系曲线，图5为体应变εv和轴向应变εa的关系曲线。由图4可以看出，饱和砂卵石土和非饱和砂卵石土试样的偏应力-轴向应变关系曲线最终都趋于恒定值，说明达到一定的应力水平后，试样已经破坏，偏应力将不再随轴向应变的变化而变化。偏应力与轴向应变的关系受围压的影响较大，当轴向应变一定时，围压越大，偏应力越大。对于粗颗粒土，含水率越高，颗粒间咬合作用越弱，相应的强度也越低。在相同围压条件下，当轴向应变达到15%时，饱和样的偏应力相比非饱和样小20.4%～24.8%。

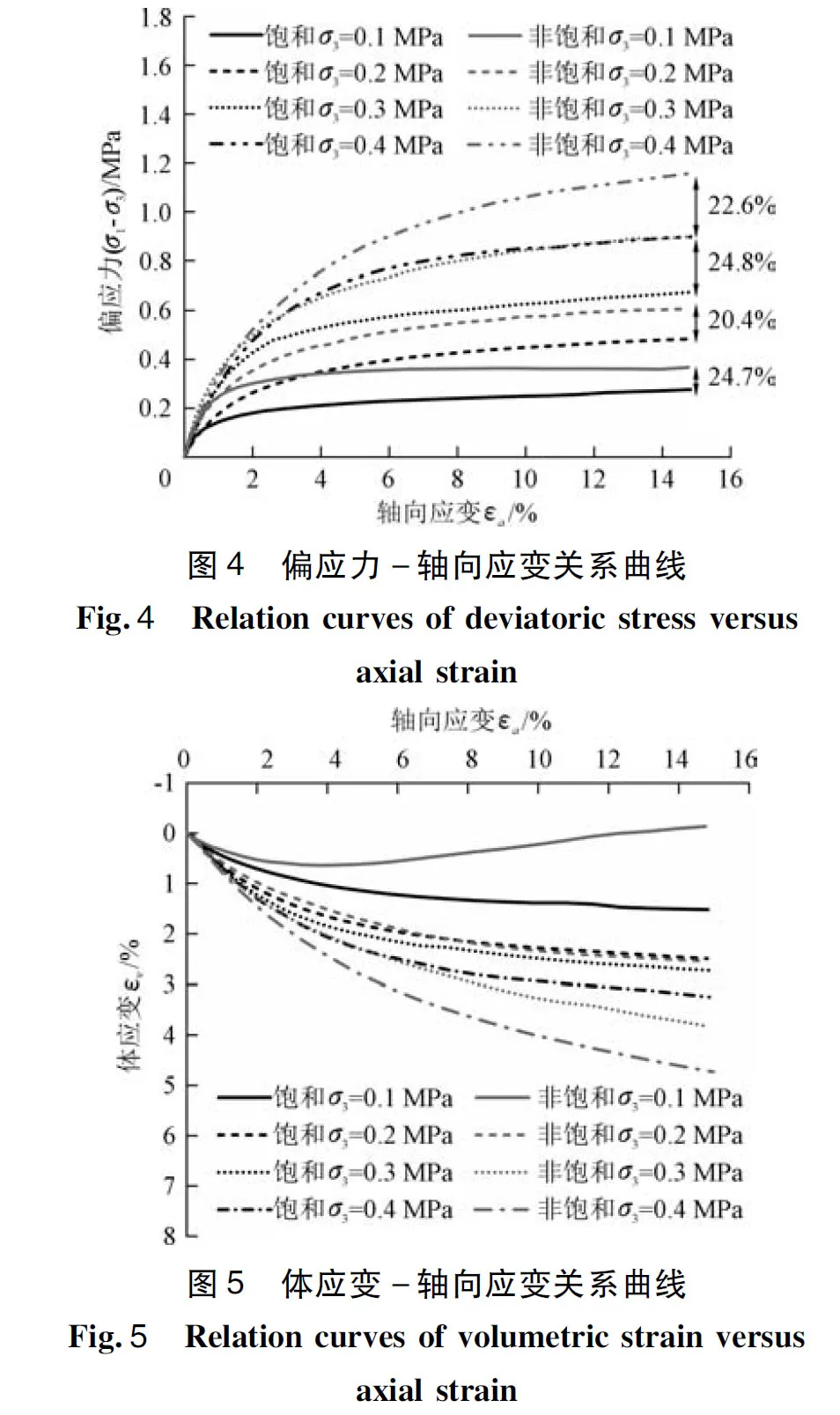
饱和砂卵石土和非饱和砂卵石土试样的体应变随围压的增大而增大，在高围压下均表现出明显的剪缩特性，不同的是饱和样在低围压下仍表现剪缩特性，而非饱和样在低围压下则表现出明显的剪胀特性。

根据三轴试验结果整理得出了饱和砂卵石土和非饱和砂卵石土试样的邓肯模型参数，如表2所示。可以看出，饱和试样黏聚力Cd值为20 kPa，摩擦角Φd值为30.5°，抗剪强度指标一般。非饱和试样的黏聚力Cd值为22kPa，摩擦角Φd值为35.0°。对于相同干密度的砂卵石土，饱和样的抗剪强度指标明显小于非饱和样，说明在富水砂卵土地区的地基强度值得关注。

表2 邓肯模型参数

4 界面剪切特性研究

对砂卵石土与混凝土面板进行接触面剪切特性试验研究，在大型叠环剪切仪的下剪切盒中填装混凝土面板，并养护至规定要求，在上剪切盒中填装砂卵石土，上覆压力σn分别为100、200、300、400 kPa。图6为大型接触面剪切特性试验的剪切应力与剪切底盒之间位移的关系曲线，可以看出接触面剪切应力随着剪切位移的增加逐渐变大，接触面剪切应力τ与剪切位移ωs基本可以用双曲线关系表示。图7为接触面抗剪强度与竖向应力的关系曲线，可以看出接触面抗剪强度随着法向应力的增大呈线性增大趋势，经拟合分析砂卵石土与混凝土面板接触面黏聚力为77.3 kPa，摩擦角为29.2°。

Clough-Duncan非线性弹性本构模型是一种典型的土与接触面本构模型[8]，可以较好地反映粗粒土与接触面间的应力-应变关系。模型假设剪切应力τ与剪切位移ωs之间存在双曲线关系，即

(1)

式中：a为初始剪切劲度系数κsi的倒数，即a=1/κsi；b=Rf/τf，接触面的抗剪强度τf=σntanφ+c，Rf为破坏比，表示接触面抗剪强度与极限剪切剪应力的比值，c为接触面的黏聚力。

初始剪切劲度系数κsi为接触面上法向应力σn的幂函数，即

(2)

接触面的剪切劲度系数κst为

(3)

式中：κi为无因次的劲度系数；n为劲度指数；φ为接触面的摩擦角；Pa为大气压力；γω为水的重度。

Clough-Duncan模型中5个基本参数(κi、n、c、φ、Rf)代表了与应力有关的接触面特性，根据本次接触面剪切特性试验结果拟合分析得到模型参数如表3所示。

表3 Clough-Duncan接触面模型参数

5 流变特性研究

流变是指土体受力变形中存在的与时间有关的变形特性，在大型高压三轴仪上对砂卵石土开展三轴流变试验研究其长期流变特性。三轴流变试验采用应力式加载，围压与三轴剪切试验保持一致，对应应力水平SL分别为0.2、0.4、0.6、0.8。流变试验过程中保持实验室温度恒定(20±1) ℃以消除温度变化对试验结果的影响。流变试验中需要监测轴向变形和体积变形，根据规范[12]要求，粗粒土三轴流变试验稳定标准取为每24 h内轴向应变的变化量<0.05%。

图8(a)和8(b)分别为砂卵石土流变试验中轴向应变和体积应变随加载时间的变化曲线。从图8可以看出，砂卵石土的流变在加载前期较为显著，此后流变速率逐渐减小，流变与加载时间的关系曲线趋于平缓。对比不同压力条件下的流变试验结果可以发现，应力水平越大，流变曲线趋于平缓的时间越早。

按照滞后变形理论，粗粒料流变过程中的总应变由瞬时产生的弹塑性应变和滞后产生的黏滞应变(即流变)两部分组成[13]。弹塑性应变和黏滞应变的分割点根据试验初期应变速率确定。为区分两部分应变，对流变过程中的轴向应变与时间关系曲线直线段的起始时间进行统计，直线段起始时间的平均值约为1 h。因此本次在整理流变试验成果时，统一认为两部分应变时间以1 h为界，1 h以前的应变为初始弹塑性应变。1 h之后的应变为黏滞应变。

将砂卵石土流变试验成果整理在双对数坐标系下，以围压σ3=0.1 MPa的试验为例，图9(a)和9(b)分别为不同应力水平下轴向变形和体积变形的流变量与时间关系曲线。从图中可以看出，在双对数坐标系下流变试验中轴向应变和体积应变随加载时间线性增长，说明采用幂函数来描述砂卵石土的流变特性是较为合理的。

已有研究发现筑坝堆石料的流变量和剩余流变量与时间在双对数坐标系下均成线性关系，其流变量与时间的关系可采用幂函数描述，基于此长江科学院提出了针对筑坝堆石料的9参数流变模型[9-10]。经分析砂卵石土的三轴流变试验结果中流变量与时间的关系也遵循上述关系，但砂卵石土的初始变形量较大，直接采用筑坝堆石料9参数流变模型会导致轴向应变与围压的关系表达式不通过0点，因此增加了2个参数(a、b)对原表达式进行修正。

根据滞后变形理论，总应变包括瞬时产生的弹塑性应变Δεep和滞后产生的黏滞应变ΔεL(t)两部分，即

Δε=Δεep+ΔεL(t) 。

(4)

采用幂函数来表达流变量与时间的关系为

εL=εf(1-t-λ) 。

(5)

由式(4)和式(5)可得剩余流变量为

(εf+εep)-ε=εft-λ。

(6)

剩余流变量与时间关系曲线在双对数坐标下呈现良好的线性关系，根据不同时间t的应变拟合εf、λ，且εf、λ为应力状态的函数，即：

(7)

(8)

式中a、b、c、d、η、m完整地给出轴向流变特征。

体积流变量与时间关系可以采用幂函数表示为

εLV=εfV(1-t-λV) 。

(9)

通过拟合不同时间t的应变εLV可得εfV、λV，且εfV是应力状态的函数，其表达式为

εfV=cαsLdα+cβsLdβσ3。

(10)

式中ca、da、cβ、dβ为体变流变指标。

以上11参数流变模型可较好地反映砂卵石土的流变特性。表4为整理本次砂卵石土流变试验成果得到的11个流变参数，参数对应的时间单位为h，应力单位为MPa。

表4 砂卵石土11参数流变模型参数

6 结 论

针对某大型悬索桥锚锭基础下覆砂卵石土系统开展三轴剪切试验、界面剪切试验及三轴流变试验，分析试验成果选取合适的力学模型描述砂卵石土的应力应变关系，并整理出相应的模型参数，主要结论如下：

(1)砂卵石土三轴剪切试验中轴向应变一定时，围压越大，偏应力越大，体积应变越大。在相同围压下，当时轴向应变相等时，饱和样的偏应力要小于非饱和样。在低围压下砂卵石土饱和样和非饱和样分别表现出剪缩特性和剪胀特性，而在高围压下则均表现出明显的剪缩特性。根据试验结果整理得到砂卵石土邓肯模型参数，非饱和砂卵石土试样的各项抗剪强度指标较饱和试样有较大提高，说明在富水砂卵土地区的地基强度值得关注。

(2)砂卵石土与混凝土接触面上剪应力与剪切位移基本可以用双曲线关系表示，抗剪强度随法向应力的增大而线性增大。

(3)砂卵石土的流变变形中轴向应变和体积应变双对数坐标系下均随时间线性增长，采用幂函数可较好地描述砂卵石土的流变发展规律。基于三轴流变试验结果提出了砂卵石土11参数流变模型，该模型可以较好地反映砂卵石土的流变特性。