基于长期与中长期嵌套的水库优化调度

孙桂凯，石 锐，刘思怡，王国帅，赵荣娜，莫崇勋

(1.广西大学 土木建筑工程学院，南宁 530004； 2.广西大学 工程防灾与结构安全教育部重点实验室，南宁 530004；3.广西大学 广西防灾减灾与工程安全重点实验室，南宁 530004)

1 研究背景

我国西南部喀斯特地区，降水丰沛，蕴含大量喀斯特水资源[1]，但由于强烈的喀斯特作用，地表水快速地转变为地下水，加上已有的技术仍然无法将喀斯特区的地下水进行合理开发，造成该区域存在工程性缺水问题，甚至部分区域已经成为中国缺水最严重的地区之一。该地区水库有多年平均弃水量大、汛末蓄满率低的特点。因此，西南地区水库优化调度研究对于提高水资源利用率、改善西南地区水资源紧缺现状具有重大意义。近些年来，随着计算机的计算能力大幅提升，传统算法及智能算法不断被改进及应用，水库优化调度方面的研究取得了丰硕的成果[2]。Tinoco等[3](2016年)利用长系列模拟对比优化方法，探讨了多种水库调度方案模式在以农业用水为主要兴利目标的厄瓜多尔马库尔流域的应用效果，结果能为该流域控制水库的水资源调度管理决策提供参考，同时还对水库灌溉泄水渠道提出了优化建议；周华艳等[4](2018年)使用烟花粒子群算法对水库联合优化调度方案决策进行研究，验证了烟花粒子群算法求解的高效性；Zhang等[5](2018年)提出利用前沿的长短期智能储存算法来协调水库月尺度、日尺度和时尺度优化调度运行方案间存在的矛盾，并与经典神经网络、支持向量机等初级智能算法在求解水库优化调度问题上的效率与结果进行了对比，对水库调度决策智能调整研究进行了初探；李家叶等[6](2018年)采用SOA(Serrice-Oriented Architecture)架构对不同尺度不同模型的水库调度方案决策进行研究，建立的系统能够快速集成分析相关水情数据，开展梯级水库优化调度演算，及时为决策者提供清晰有效的决策辅助信息；李文武等[7](2018年)针对长期随机调度的维度灾害问题，在描述来水随机过程的基础上，提出了基于强化学习理论的水库长期优化调度模型，采用机器学习中基于模型(model-based)的SARSA(State Action Reward State Action)算法，且考虑入库随机变量的马尔可夫特性，通过贪婪决策与近似值迭代，调整学习参数，求解出近似最优序列。

多数研究都是基于月尺度对模型的求解算法进行优化的，这无法使水库的工程效益最大。而传统的动态规划算法，以日尺度进行优化求解时，随着决策变量的增加，计算会出现“维数灾”等问题。鉴于此，本文提出水库长期优化调度与中长期优化调度嵌套模型，在动态规划中耦合遗传算法，形成月-日尺度嵌套水库调度模型，并将其应用于水库防洪与发电优化调度中，验证了该模型的可行性。

2 水库优化调度嵌套模型

优化调度最主要的内容是建立调度模型，水库优化调度模型就是面对不同阶段水库蓄水量，逐步决策水库泄水[8]。在调度模型方面，水库优化调度模型可以分为隐随机优化模型、显随机优化模型和参数模拟优化模型[9-10]，各模型在调度信息的模拟方式、求解效率和适用性上有着各自的优缺点。其中，参数模拟优化模型因能描述水文序列和预报的不确定性，能耦合多种预报模型进行滚动实时调度，能挖掘水库调度潜力，成为目前多数研究中构建调度模型的首选形式[11]，故本文构建参数模拟优化模型以实现水库优化调度的研究。

考虑水库长期效益与短期效益的协调关系，建立将长期优化调度与中长期优化调度进行嵌套的优化调度模型。宏观上，长期优化调度从全周期视角出发，以长期径流预报数据作为输入，结合水库长期调度计划和基本约束条件，确定全周期中各个时间节点的调度边界，如时段末水位、时段泄水量和时段来水量等关键信息。微观上，长期优化调度时段决策集转移至中长期优化调度模型中，将该范围作为中长期优化调度模型嵌入的软边界条件，以日均径流量作为调度基础数据，求解出中长期优化调度决策范围，完成不同时间尺度优化调度的嵌入。

2.1 目标函数

为保障水库防洪与兴利的目标，采用约束法[12]将防洪目标转换为硬性约束，坝前水位均不超过汛限水位，在满足防洪的前提下，将多目标问题转化为以发电量最大化的单目标问题。长期优化调度和中长期优化调度的目标函数表达式分别为：

(1)

(2)

式中：ECQ、EZQ分别为长期优化调度下和中长期优化调度下总发电量(kW·h)；T1、T2分别为以年为调度周期和以月为调度周期的时段总数；K为水库的出力系数；qet1、qet2分别为在时段t1和时段t2内的发电流量(m3/s)；Ht1、Ht2分别为Δt1和Δt2时段内的水头(m)。

2.2 约束条件

水库调度过程需满足以下约束条件：

①水量平衡方程为

Vi=Vi-1+(qi-Qi-qsi)Ti；

(3)

②库容约束条件为

Vmin≤Vi≤Vmax；

(4)

③水位约束条件为

Zmin≤Zi≤Zmax；

(5)

④下泄流量约束条件为

Qi≤Qmax=Qf；

(6)

⑤出力约束条件为

Nmin≤Ni≤Nmax。

(7)

式中：Vi-1、Vi分别为第i时段初、末的水库蓄水量(万m3)；qi、Qi、qsi分别为第i时段的水库入库流量、发电流量和下泄流量(m3/s)；Ti为第i时段时长(s)；Vmin、Vmax分别为t时段末水库的蓄水量(万 m3)下限和上限(在长期发电调度中，Vmin一般为死库容，Vmax在汛期表示汛限水位对应的库容、枯水期表示正常蓄水位对应的库容)；Zi、Zmax、Zmin分别为水库所允许的第i时段的小位(m)和最高、最低水位(m)(在长期调度中，Zmax一般在汛期取汛限水位、枯水期取正常蓄水位，Zmin一般取死水位)；Qf为澄碧河下游安全泄量(m3/s)；Qmax为水库下泄流量(m3/s)上限；Nmax、Nmin分别为电站的最大出力和最小出力(kW)，一般取水电站的装机容量和保证出力。

将式(3)—式(7)作为目标函数的约束条件，与目标函数一同构成水库优化调度嵌套模型。在中长期调度中，以长期调度确定的后汛期库容以及水位作为边界，注意在计算时要区分长期优化调度和中长期优化调度对应参数。

3 模型求解

水库优化调度模型求解技术分为两大类：一是包含线性规划、混合整数规划、动态规划等[13-14]确定性优化算法，二是如遗传算法、退火算法、粒子群算法等[15-16]智能优化算法。两类方法在求解不同时空尺度和约束条件下的调度模型时有着各自的适用性，长期优化调度决策方案求解宜采用确定性优化算法，而中长期及短期优化调度决策方案求解宜采用智能优化算法[17]。本研究中长期优化调度采用动态规划算法，中长期优化调度采用遗传算法。

3.1 动态规划算法

动态规划算法(Dynamic Programming)是一种多阶段决策过程(或称分析系列系统)最优化的数学规划方法。动态规划算法的应用十分广泛，可用于工程建设、生产、科研和管理等许多与阶段性相关的问题中，例如线路最优选择、资源的分配、水库调度、结构设计优化等问题，都可以采用动态规划算法进行相关计算并解决。动态规划算法的基本原理是最优化决策序列只与当前的状态及目标有关，而与过去的历史无关。关于多阶段的决策问题，多数是与时间历时有关的问题，其中最典型的为水库优化调度问题，笔者将它当作“动态的系统”，用动态规划算法来求解，求解流程如图1所示。

图1 动态规划算法求解流程示意图Fig.1 Schematic diagram of dynamic programming

3.2 遗传算法

遗传算法(Genetic Algorithm)是人工智能方法的一种，该算法通过模拟自然界中选择与遗传过程时存在的繁殖、交叉和基因突变现象，经过不断地迭代更新，直到满足某种收敛指标为止，即优化问题的最优解。通过对比传统启发式优化搜索算法，可以看出遗传算法的本质特征是群体搜索策略和遗传算子。群体搜索能够实现遗传算法突破领域搜索的需求，能够帮助信息在整个解空间上进行收集和探索，同时遗传算子通过适应值的度量来对运算指标随机操作，这种做法能够有效地削弱启发式算法搜索过程中对于人机交互的依赖。这种多个方向进行全局优化的特点，能够为目前诸多复杂的问题提供良好的理论价值。遗传算法计算流程见图2(a)。根据上述动态规划算法及遗传算法计算流程综合可得优化调度嵌套模型的计算流程，如图2(b)所示。

图2 计算流程Fig.2 Flowchart of calculation

4 实例应用

4.1 工程概况

澄碧河水库的坝址位于广西壮族自治区百色市，地理坐标为106°38′E、23°57′N，是一座具有发电、防洪、养鱼、供水等综合利用功能的大(1)型水利枢纽工程。水库坝址以上的集雨面积为2 000 km2，占流域总面积的 95.8%，其中喀斯特区面积高达400 km2，约占水库集雨面积的20%，是一座具有多年调节性能的水库。大坝设计洪水标准为：1 000 a一遇洪水设计，10 000 a一遇洪水校核，相应的设计洪水位187.96 m(珠江基面高程)，校核洪水位189.29 m，正常蓄水位185.00 m，总库容11.21亿m3。本文计算基于澄碧河水库1963—2014年水文序列资料。

4.2 结果分析

本文采用水文频率分析法[18]进行典型年的确定，该方法对澄碧河坝首站1963—2014年年径流量数据进行P-Ⅲ型适线，最终选取保证率为75%(1985年)、50%(1987年)、25%(2012年)的水文年作为枯、平、丰典型年。确定典型年后，将典型年实际入库流量输入优化调度嵌套模型计算，得到1985年、1987年和2012年坝前水位和出库流量控制计算结果，见图3(a)、图3(b)。同一典型年不同调度方式坝前水位与出库流量见图4。

图3 不同典型年 坝前水位和出库流量Fig.3 Water level in front of dam and reservoir’s outflow rate in different typical years

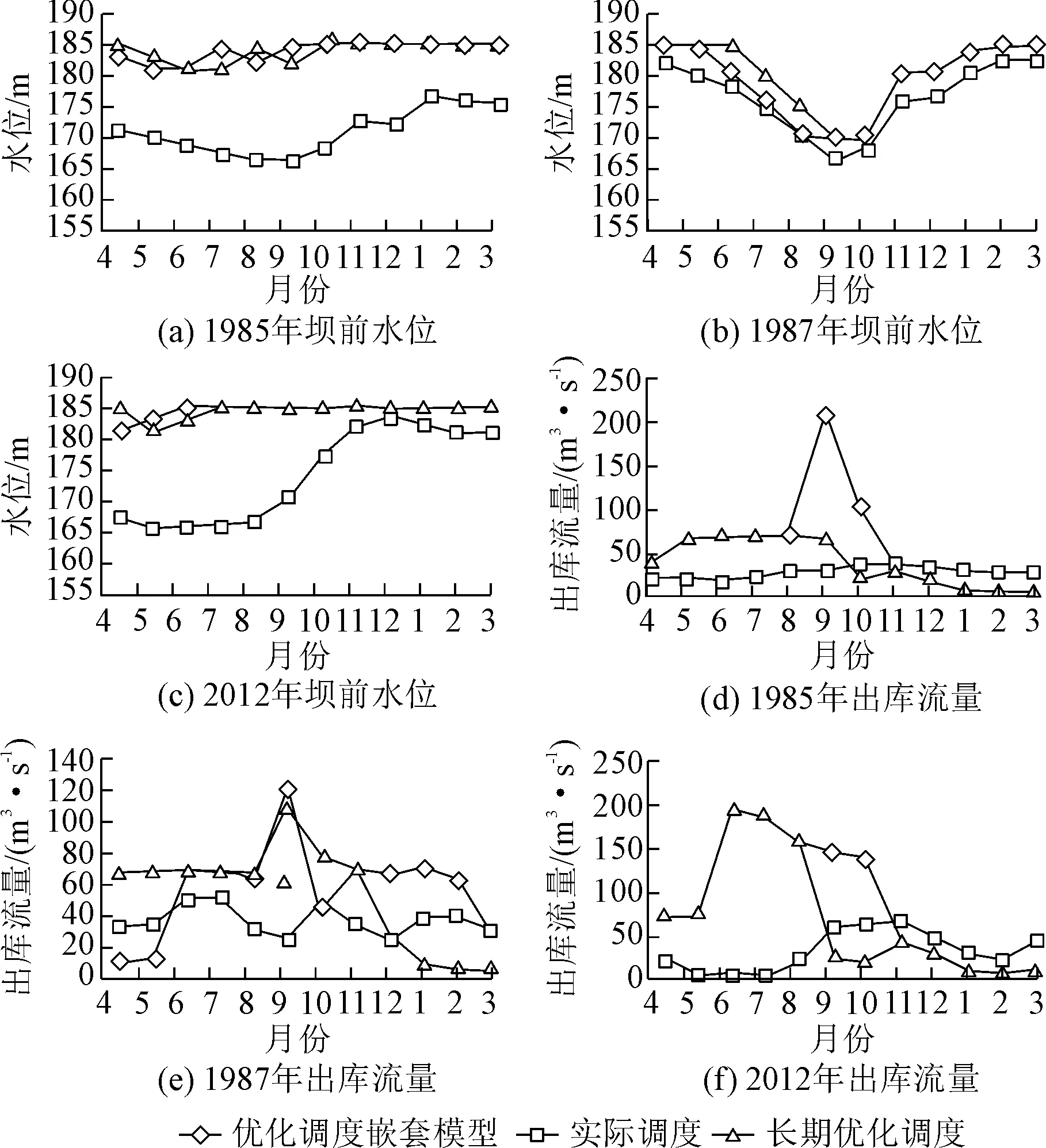
图4 3个典型年不同调度方式坝前水位与出库流量控制Fig.4 Control water level in front of dam and reservoirs outflow rate under different scheduling modes in three typical years

根据优化调度嵌套模型和长期优化调度模型的计算结果，对澄碧河水库进行模拟调度，计算1985年、1987年和2012年的发电量。统计典型年依据不同调度方案进行仿真调度后发电量，见表1。

表1 不同调度模式下典型年发电量对比

由表1可知，基于优化调度嵌套模型和长期优化调度的决策方案进行澄碧河水库的模拟调度时，在枯水年(1985年)产生的年发电量分别15 841.22万、15 206.50万 kW·h；在平水年(1987年)产生的年发电量分别20 655.83万、19 463.81万 kW·h；在丰水年(2012年)产生的年发电量分别17 911.25万、15 748.39万 kW·h。由此可见，各典型年产生的发电量均远高于现行方案下的水库发电量。其中，优化调度嵌套模型的决策方案和长期优化调度模型的决策方案产生的发电量与现行方案相比，枯水年的同比增长率分别为43.36%、37.61%，平水年的同比增长率分别为69.50%、59.72%，丰水年的同比增长率分别为73.16%、52.25%。而按优化调度嵌套模型的决策方案进行调度时，产生的年发电量较长期优化调度方案下的发电量而言，提高了5.74%～20.91%。

进一步分析各调度模型下年内发电量可知，优化调度嵌套模型求解的调度方案在9、10月份与长期优化调度的方案相比，产生了更多的发电量，究其原因在于9、10月份的调度方案发生了变化。根据课题组研究[19]，9、10月份为澄碧河水库的后汛期，是中长期优化调度嵌入的时期，该时期的方案以长期优化调度确定的月初、月末水位作为软边界，根据每月的预测入库流量以日为步长进行调度决策确定。由于长期优化调度以长期效益为目标进行全局统筹制定调度方案，而中长期优化调度则侧重于短期效益。因此，相比于长期优化调度，嵌套模型求解的优化调度方案先以全年发电量最大为目标，再对9、10月份进行中长期优化调度，能够将水库的长、短期效益进行有效协调，避免顾此失彼，明显地提高了水库发电量。

5 结 论

(1)通过优化调度嵌套模型调度方案、长期优化调度方案和现行调度方案对比，可知嵌套模型调度方案下水库发电量最大，且在后汛期发电量提升最为明显。

(2)水库长期与中长期优化调度嵌套模型优化调度方案解决了单一尺度调度方案无法有效协调防洪目标与发电目标的问题，可以平衡水库调度长期和短期之间的效益矛盾，有效提高水电站运行的综合效益。