饱和软黏土应变累积特性及经验模型

孙 磊

(宿州学院 资源与土木工程学院，安徽 宿州 234000)

1 研究背景

饱和软黏土在交通荷载下的变形特性一直是土动力学研究的重要课题之一，是进行高速公路、高速铁路、城市地铁以及机场跑道等交通基础设施结构设计、建造、服役安全评估以及运营维护的重要依据。因此，构建一个能够反映交通循环荷载作用特点的饱和软黏土应变累积模型对从变形的视角预测现有交通基础设施的服役寿命，进而改进风险评估和工程设计方法至关重要。

过去几十年国内外专家学者针对不同区域的饱和软黏土在交通循环荷载作用下的变形特性开展了大量的试验及理论研究工作，并取得了较为丰硕的研究成果，尤其体现在饱和软黏土应变累积预测模型的构建方面。自基于路基土在反复交通荷载作用下的累积变形随循环加载次数的发展特点提出指数模型以来，众多专家学者在其基础上陆续进行了改进，一方面使得指数型模型可以考虑静、动偏应力水平等因素的影响[1-5]，另一方面尽可能提高预测模型的适用性[6-8]。然而上述模型都未能反映交通循环荷载下地基土体处于部分排水的实际工况[9-11]以及交通循环荷载引起的水平向循环正应力的影响[12-13]。部分排水条件下，模拟水平向循环正应力影响的变围压三轴循环加载试验结果表明饱和软黏土在变围压应力路径下的轴向累积应变速率明显高于围压保持恒定竖向偏应力单独循环加载的情况[14-15]。部分学者在指数模型的基础上进一步构建了考虑循环偏应力和循环围压联合效应的正常固结以及超固结饱和软黏土的轴向应变累积经验模型[16-17]。然而上述模型仅针对特定周数或是某一周数之后的应变，无法反映部分排水条件下整个循环加载过程的应变累积。此外，上述经验模型本质上是对试验结果的拟合，由于模型参数都是通过拟合实测结果确定的，因而预测结果必然会与实测值吻合较好，其适用性还有待进一步验证。

基于此，本文借助GDS(Global Digital Systems)变围压动三轴仪，以温州软黏土为研究对象，开展了一系列部分排水条件下的恒定围压(Constant Confining Pressure，CCP)以及变围压(Variable Confining Pressure，VCP)应力路径下的循环加载试验，重点探究了变围压应力路径对正常固结饱和软黏土永久轴向应变的影响规律，并建立了相应的应变累积经验模型。

2 试验条件及方法

2.1 土样制备及试验过程

试验所用软黏土试样取自温州某在建工地开挖至一定深度(5～6 m)的基坑内，采用薄壁取样法获取高质量的原状土。按照《土工试验规程》(GB/T 50123—1999)测得试验所用土体的基本物理力学指标如下[16]：密度ρ=1.61 g/cm3，相对密度Gs= 2.72，天然含水量wn= 58%，液限wL= 67%，塑性指数Ip= 33，初始孔隙比e0=1.58，渗透系数k=2.6×10-6cm/s。

所有试验均采用直径5 cm和高度10 cm的圆柱体试样，并在试样的四周贴上相同规格尺寸的滤纸作为排水路径，待试样装入三轴压力室并完成所有仪器检测之后对试样进行如下操作：

(1)在10 kPa的有效围压(设定围压310 kPa，反压为300 kPa)下对试样进行反压饱和，待孔压系数B值>0.98，则表明试样完全饱和。

(2)在100 kPa的有效围压(保持300 kPa反压恒定，增大围压至400 kPa)下对试样进行等向固结直至排水体积变化基本稳定。

(3)通过CCP和VCP试验模拟交通荷载并研究变围压应力路径对饱和软黏土在部分排水条件下永久轴向应变的影响规律。

2.2 试验方案

本试验采用应力控制循环加载方式，选择如图1所示的自定义压缩波模拟交通循环荷载。

图1 加载循环偏应力及循环围压Fig.1 Applied cyclic deviatoric stress and cyclic confining pressure

参照以往的研究设定加载频率为0.1 Hz，循环次数为10 000[9-10]。在循环加载过程中将排水阀门打开以实现排水，用于模拟交通循环荷载作用下地基饱和软黏土的实际工况。由于饱和软黏土渗透性较差，在循环动载的作用下无法实现完全排水，因而称为部分排水。然而，以现有的技术手段，应力加载模式下的动三轴试验并不能预先设定饱和软黏土试样的排水程度。实际上，如同天然土体的结构性特征一样，尽管无法进行定量表征，但是依然可以定量描述各种循环荷载对其动力特性的影响。尽管在本文的循环加载试验过程中无法预先设定部分排水的程度，但是可以通过试验结果反推循环加载过程中的排水程度。参照刘家顺等[15]采用体应变增量与轴向应变增量的比值(dεv/dε1)来量化试样的排水程度，本文所有试验的dεv/dε1约为0.98。

所有试验在循环加载过程中保持循环偏应力与循环围压的相位差为0，在保持循环偏应力恒定的情况下，改变循环围压的幅值则可以在如图2所示的p-q平面形成不同的应力路径。

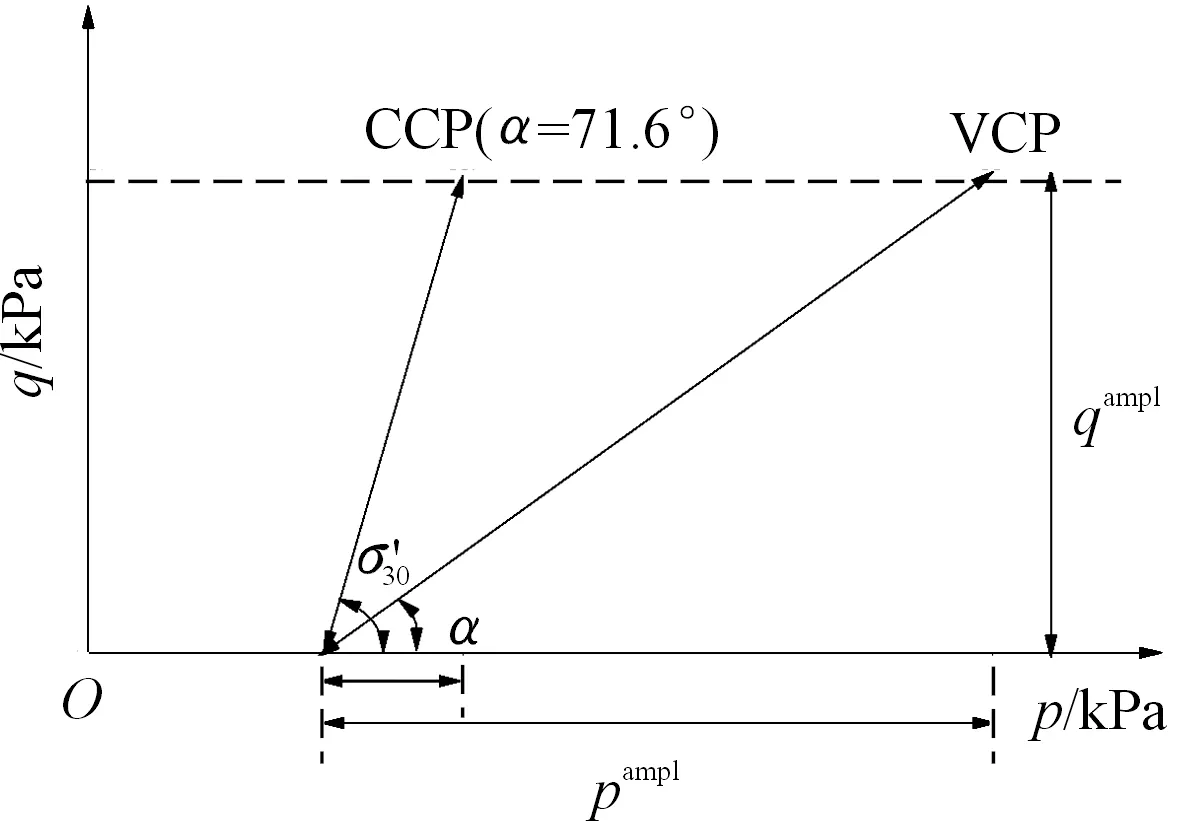
图2 循环三轴应力路径Fig.2 Cyclic triaxial stress paths

为了表征不同应力路径，Rondón等[18]定义应力路径斜率ηampl为

(1)

Cai等[14]则采用1/ηampl来反映应力路径的影响。由于ηampl或1/ηampl均与应力路径的倾角α有关，因此本文采用应力路径倾角α来表征应力路径，如图2所示，对CCP试验而言，倾角α为71.6°。

为了模拟不同的交通荷载状况和衡量循环动应力水平的影响，参照以往的研究选取不同的循环动应力幅值并定义循环应力比(CSR)为[6，15]

CSR=qampl/qf。

(2)

式中qf为三轴固结不排水单调剪切试验获得的偏应力峰值。对于本文试验所用的温州饱和软黏土，经试验测得其100 kPa 固结围压下的qf约为69 kPa。具体的试验方案如表1所示。

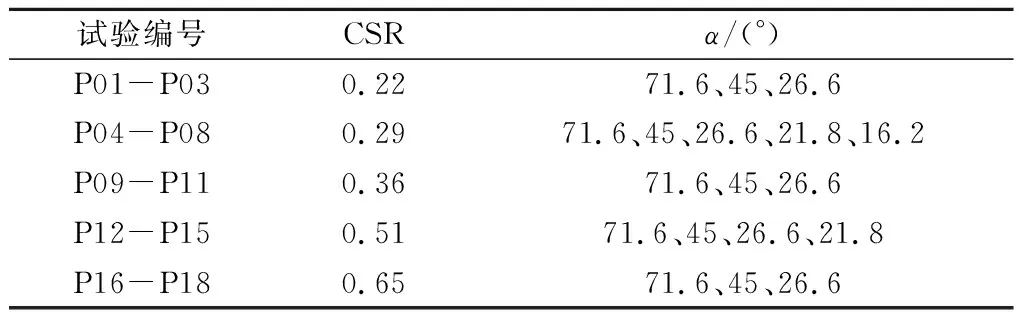
表1 循环三轴试验方案

3 试验结果及分析

3.1 典型CCP及VCP试验结果

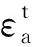
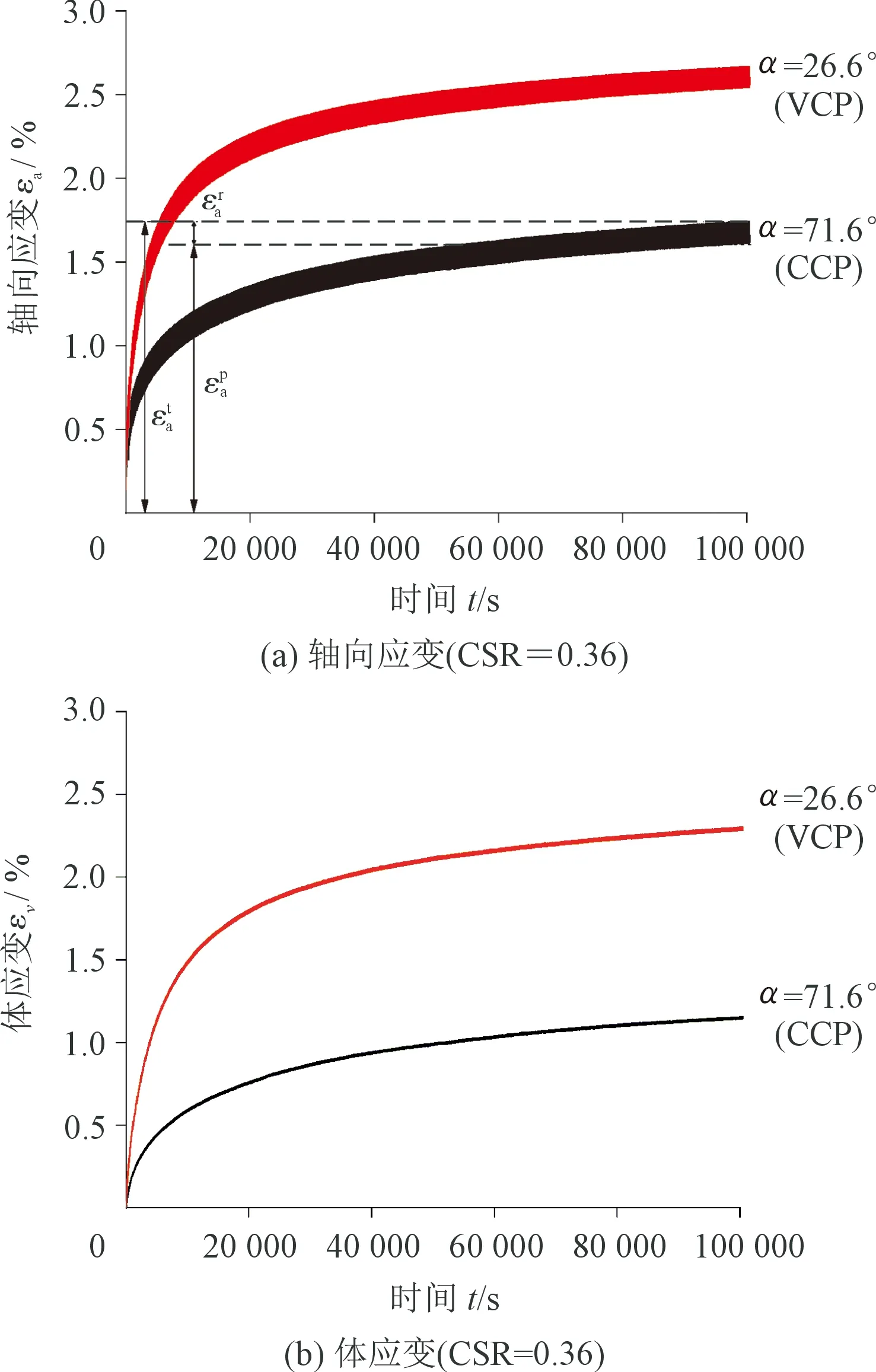
图3 CCP及VCP试验条件下试样典型的轴向应变和体应变时程曲线Fig.3 Typical time-history curves of axial strain and volumetric strain in CCP and VCP tests

图4进一步给出了部分排水条件下，CCP试验和VCP试验获得的正常固结饱和软黏土试样的典型偏应力-轴向应变关系曲线。其中循环次数N分别为1、10、100、500、1 000、5 000和10 000时的滞回曲线通过彩图加以突出显示。从图4中可以看出，VCP试验与其对应的CCP试验产生的滞回曲线形状基本类似。随着循环次数的增加，试样的永久轴向应变逐渐增长，但累积速率逐渐降低。图4进一步反映出循环围压对试样永久轴向应变具有显著的影响，当N=10 000时，VCP试验(α=26.6°)产生的永久轴向应变(2.561%)约为相应CCP试验(α=71.6°)产生的永久轴向应变(1.603%)的1.6倍。

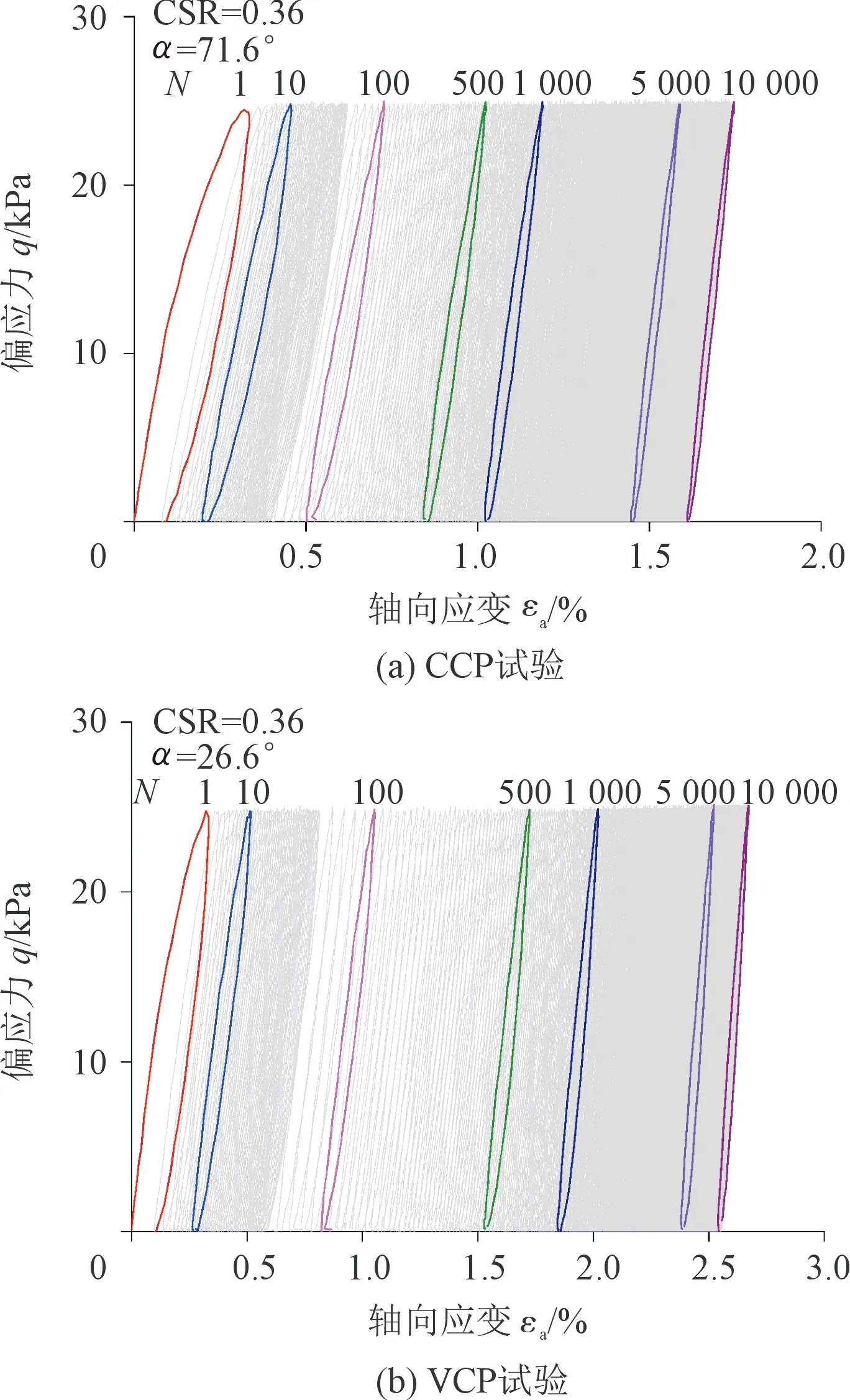
图4 CCP及VCP试验条件下试样典型的偏应力-轴向应变关系曲线Fig.4 Typical curves of cyclic deviatoric stress versus axial strain in CCP and VCP tests

通过图4还可以看出滞回曲线所围成的面积随着循环次数的增加逐渐减小，说明试样在循环荷载作用下发生变形时耗散于土体内部的能量逐渐减小。莫海鸿等[19]将其定义为黏滞能量耗散，包括塑性能和内能两部分，其中塑性能主要导致饱和软黏土微观结构形态以及黏聚力的改变而产生塑性应变，而内能则导致土颗粒的移动以热能的形式存储于土体中，因此滞回曲线为一不闭合的曲线。

3.2 永久轴向应变发展规律

图5(a)和图5(b)分别给出了部分排水条件下，试样在相同应力路径(α=45°)不同循环动应力比下的永久轴向应变随循环加载次数的发展曲线和试样在相同循环动应力比(CSR=0.29)不同应力路径下的永久轴向应变随循环加载次数的发展曲线。

通过图5可以看出，在半对数坐标系下，试样的永久轴向应变的发展随着循环加载次数的增加可以近似分为3个阶段：①初始缓慢增长阶段(N=1～10)，试样的永久轴向应变在前10次循环基本呈线性缓慢累积；②快速增加阶段(N=10～1 000)，试样在该阶段的永久轴向应变随着试样中孔隙水的不断排出迅速累积，试样在这一阶段产生的永久轴向应变占试样在整个循环加载过程中产生的永久轴向应变的50%以上；③压密稳定阶段(N=1 000～10 000)，试样在前1 000次循环加载过程中不断被压密以至于在后续循环加载过程中塑性应变的累积速率逐渐降低并趋于稳定。

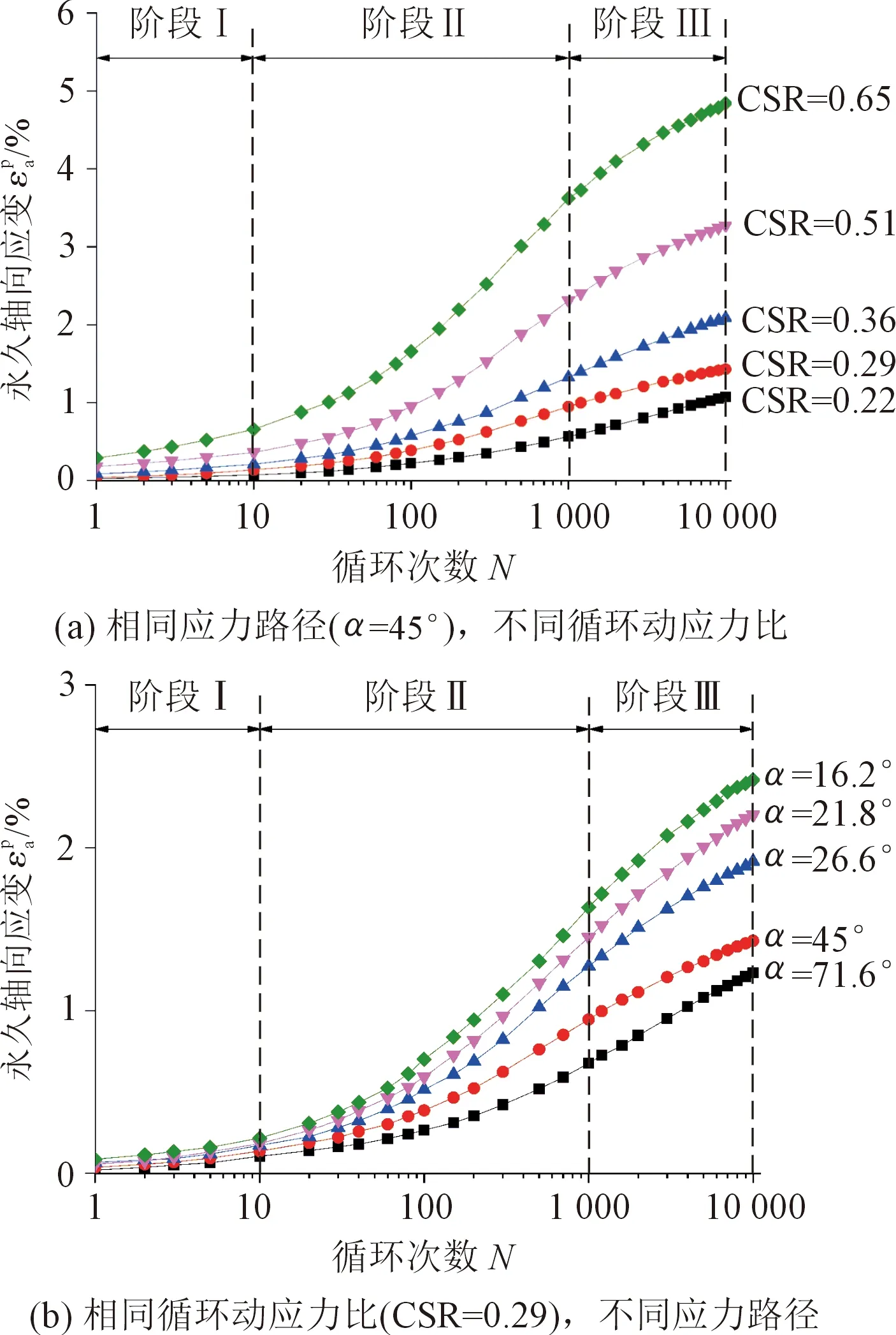
图5 部分排水条件下试样永久轴向应变随循环加载次数的变化曲线Fig.5 Permanent axial strain versus number of load cycles from partially drained cyclic triaxial tests

上述现象与排水条件下，铁路道砟碎石路基材料在单向纯压循环荷载作用下永久轴向应变随循环加载次数的发展规律类似[20]。此外，图5还表明，在其他条件相同的情况下，循环动应力比(CSR)以及应力路径倾角(α)均表现出对试样永久轴向应变一致的影响规律，即CSR值越大或α值越小，试样产生的永久轴向应变就越大。

图6进一步给出了图5中循环次数N取10、50、100、500、1 000、5 000、10 000时试样永久轴向应变分别随CSR和α值的变化曲线。从图6(a)中可以看出试样在相同的应力路径(α=45°)及循环次数下，永久轴向应变随着循环应力比的增大呈指数规律增长，可用式(3)加以描述，即

(3)

式中a1和b1为与循环次数N及应力路径倾角α相关的拟合参数。

从图6(b)中可以看出试样在相同的循环应力比(CSR=0.29)及循环次数下，永久轴向应变随着α值的增大呈对数规律衰减，可用式(4)加以描述，即

(4)

式中a2和b2为与循环次数N及循环应力比CSR相关的拟合参数。

图6 给定循环次数下试样永久轴向应变分别随CSR和α值的变化曲线Fig.6 Permanent axial strain versus CSR and α values under given number of cycles

进一步通过式(3)拟合不同应力路径下试样循环加载10 000次时的永久轴向应变与CSR值之间的关系，如图7(a)所示；通过式(4)拟合不同循环应力比下试样循环加载10 000次时的永久轴向应变与α值之间的关系，如图7(b)所示。

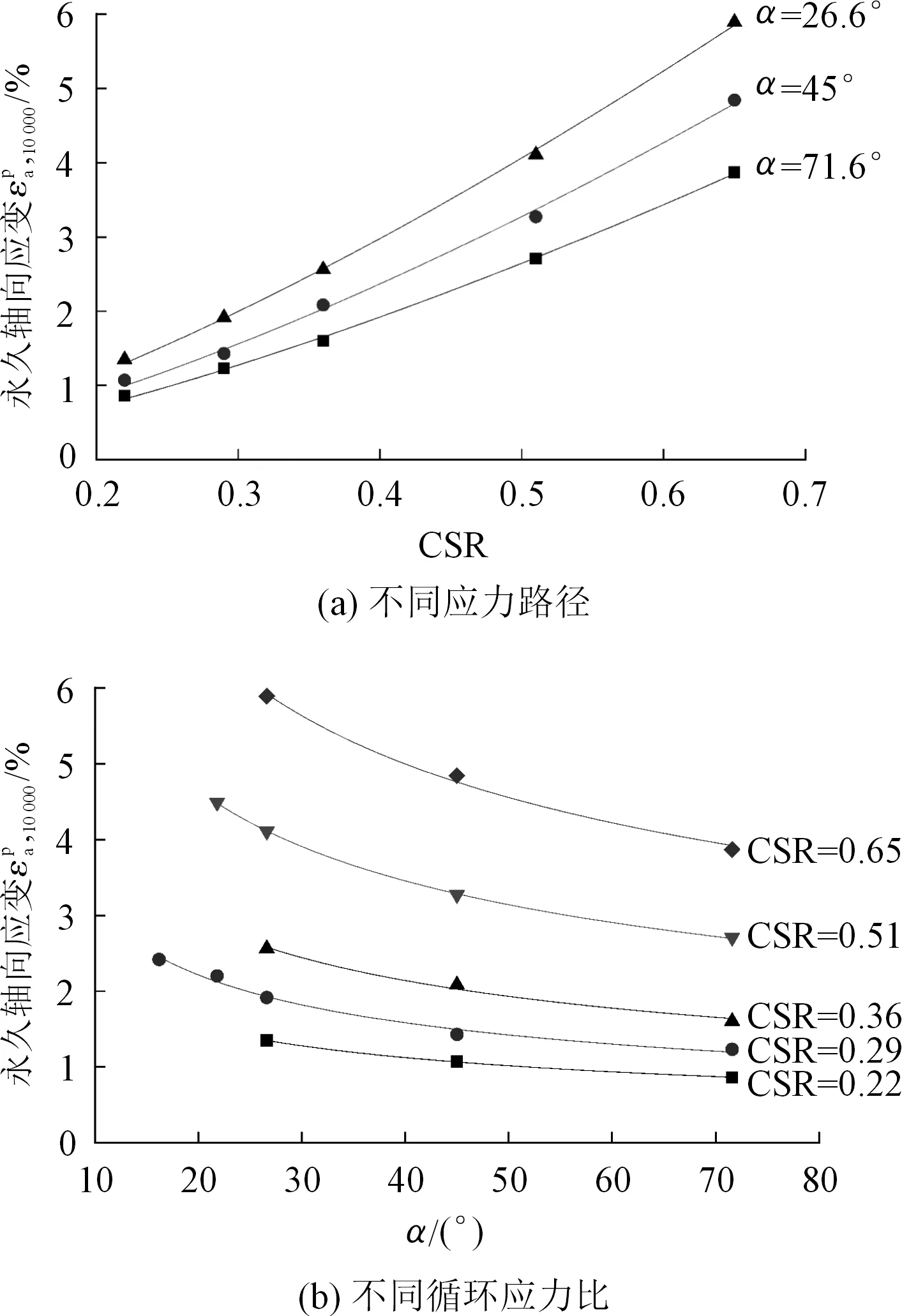
图7 10 000次循环加载下试样永久轴向应变分别随CSR和α值的变化曲线Fig.7 Permanent axial strain undergone 10，000 cycles versus CSR and α values

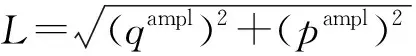
图8 10 000次循环加载下试样永久轴向应变与应力路径长度之间的关系Fig.8 Permanent axial strain undergone 10，000 cycles versus the length of stress path

(5)

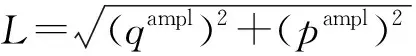
(6)

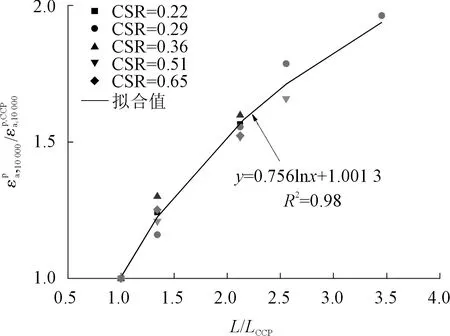
图9 归一化10 000次循环加载下试样永久轴向应变与归一化应力路径长度之间的关系Fig.9 Normalized permanent axial strain undergone 10，000 cycles versus normalized length of stress path

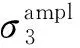
图10 10 000次循环加载下试样永久轴向应变与平均主应力幅值之间的关系Fig.10 Permanent axial strain undergone 10，000 cycles versus the amplitude of mean principal stress

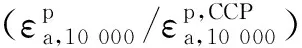
(7)

联合式(2)、式(3)、式(7)以及应力路径α可以进一步得到预测本文试样在给定循环偏应力幅值(qampl)和不同应力路径(α)作用下循环10 000次的永久轴向应变公式，即

(8)

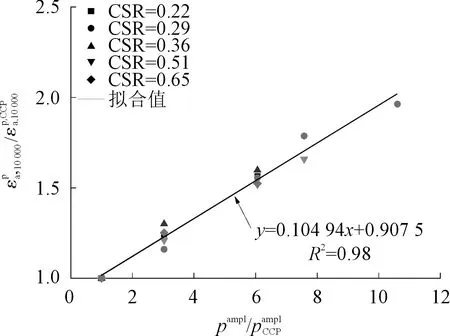
图11 归一化10 000次循环加载下试样永久轴向应变与归一化平均主应力幅值之间的关系Fig.11 Normalized permanent axial strain undergone 10，000 cycles versus normalized amplitude of mean principal stress

3.3 永久轴向应变预测模型

根据之前的分析可知，在部分排水条件下，试样在经过1 000次循环加载后的永久轴向应变逐渐趋于稳定，因此本文基于所有试样在前3 000次循环加载下产生的永久轴向应变建立经验模型用于预测试样在整个10 000次循环加载过程中产生的永久轴向应变，并与实测值进行比较以验证所构建经验模型的可靠性。Wichtmann等[21]通过大量的砂土排水循环加载试验指出对数型模型更加适用于描述压缩型曲线。因此，本文采用如下对数型模型对试样结果进行拟合，即

(9)

式中C1、C2为拟合参数，与施加的动应力水平有关。

采用式(9)对恒定围压下试样在前3 000次循环加载下产生的永久轴向应变进行拟合，拟合结果如图12所示。

图12 α=71.6°时恒定围压下试样永久轴向应变实测值与拟合值Fig.12 Experimental and predicted permanent axial strain in CCP tests when α=71.6°

为了进一步分析循环动应力比CSR对拟合参数C1、C2的影响，将不同循环动应力比下的拟合参数列于表2。

表2 恒定围压下轴向永久应变拟合参数

从表2可以看出，拟合参数C1随着CSR的增加呈下降趋势，而拟合参数C2则正好相反。如图13所示，可分别用以下指数函数定量描述CSR与拟合参数C1、C2之间的关系，即

C1=0.963CSR-1.297，R2=0.99 ；

(10)

C2=0.146CSR2.626，R2=0.99 。

(11)

将式(10)和式(11)代入式(9)可得到恒定围压下试样永久轴向应变经验公式为

(12)

图13 循环动应力比对拟合参数的影响Fig.13 Influence of CSR on fitting parameters

图14 变围压应力路径与恒定围压应力路径下试样永久轴向应变之间的关系Fig.14 Relationship of permanent axial strain in VCP test with that in CCP test

图15进一步刻画了λ与归一化应力路径倾角(α/αCCP)之间的关系。从图15中可以看出在双对数坐标下，两者之间呈线性负相关关系，说明λ与α/αCCP之间呈负指数关系，其衰减指数为-0.56，即

(13)

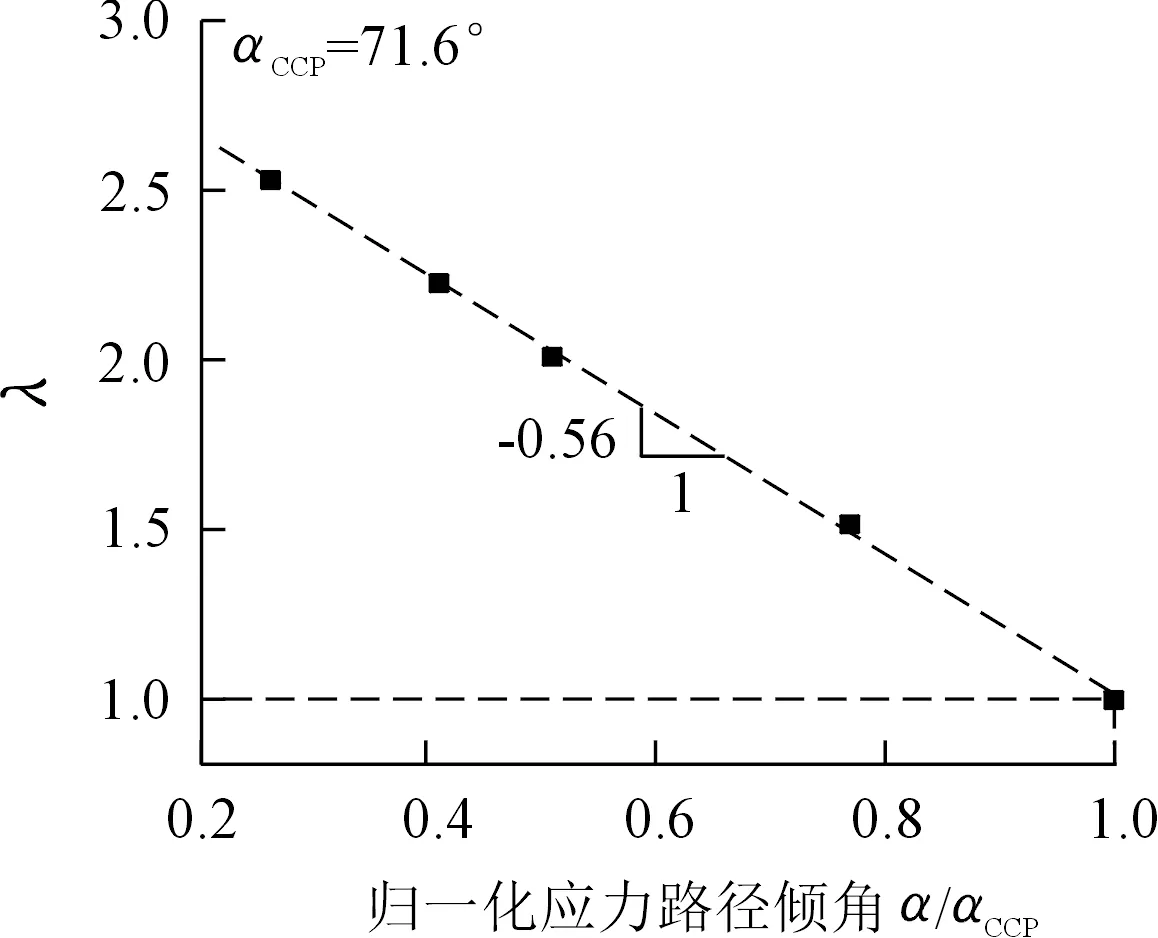
图15 λ与α/αCCP之间的关系Fig.15 Relations between λ and α/αCCP

进一步将式(12)代入式(13)则可以得到部分排水条件下考虑变围压应力路径影响的饱和软黏土永久轴向应变预测经验模型为

(14)

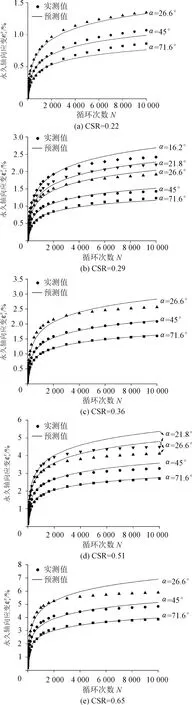
图16 实测及预测永久轴向应变Fig.16 Experimental and predicted axial permanent strains

为了验证所构建的永久轴向应变预测经验模型的适用性，图16进一步给出了利用式(14)计算得到的永久轴向应变与实测结果之间的对比。由于式(14)是基于前3 000次循环加载得到的永久轴向应变结果建立的，因此利用式(14)计算得到的试样在前3 000次循环的永久轴向应变与实测值必然吻合较好。随着循环次数的增大，除了当CSR较大和α值较小时预测的结果与实测值之间差距稍大外，但最大误差仍在20%以内，其他情况下均能够较为精确地预测试样永久轴向应变随循环加载次数的发展。考虑到实际交通循环荷载具有低幅值的特点，因此式(14)可以较好地预测部分排水条件下正常固结饱和软黏土在恒定围压以及变围压应力路径下的永久轴向应变。

4 结 论

通过不同应力路径下的三轴循环加载试验，研究了变围压应力路径对正常固结温州饱和软黏土在部分排水条件下的永久轴向应变发展规律的影响，并构建了新的考虑变围压应力路径影响的轴向应变累积模型，主要得出以下结论：

(1)地基饱和软黏土在交通循环荷载作用下产生永久轴向应变大小取决于交通循环荷载在地基土体中引起的竖向和水平向动应力幅值及其耦合应力路径。变围压三轴应力路径相对于常规恒定围压三轴应力路径能够更加真实地刻画地基土体在移动轮载反复作用下经历的复杂动态应力路径。

(2)变围压试验得到的永久轴向应变明显大于相应的恒定围压试验结果。通过归一化和拟合分析得到的结果可以定量描述应力路径α及其长度L与试样循环加载10 000次时的永久轴向应变之间的关系。

(3)在对数函数的基本框架下，基于前3 000次循环加载试验下永久轴向应变的试验结果，通过对恒定围压应力路径下永久轴向应变的拟合分析，并结合试样在变围压应力路径下的永久轴向应变与相应恒定围压应力路径下永久轴向应变之间的定量关系描述，构建了可以同时考虑循环动应力水平(CSR)、循环次数(N)以及变围压应力路径倾角(α)综合影响的永久轴向应变经验模型，且其具有良好的适用性。

(4)有必要考虑真实交通软土地基的超固结特性、加载频率以及主应力轴旋转等因素，进一步开展相关方面的研究工作，以便构建一个更加广泛且适用于我国滨海地区地基饱和软黏土永久变形预测的经验模型。