RV减速器几何回差的精确建模及试验研究

任重义,毛世民,郭学东

(1. 宁夏大学 机械工程学院,银川 750021;2. 西安交通大学 机械制造系统工程国家重点实验室,西安 710049)

RV减速器具有体积小, 重量轻, 传动比范围大, 寿命长, 精度高,效率高, 传动平稳等一系列优点,在工业机器人、数控机床等领域获得广泛应用。RV传动简图如图1所示。它由渐开线圆柱齿轮减速机构和摆线针轮行星传动机构两部分组成。RV传动有两项严格的技术指标:运动精度;回差。

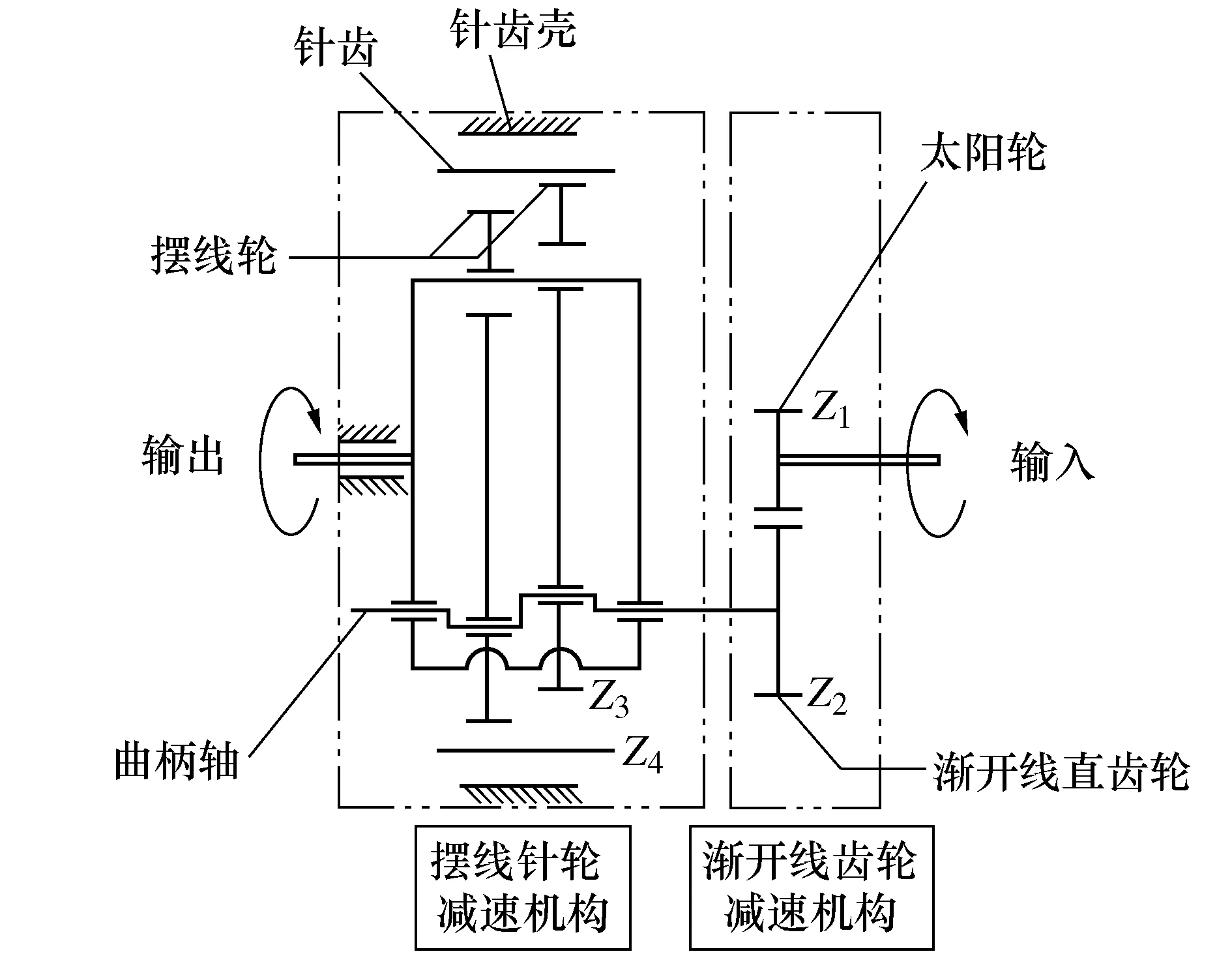
图1 RV传动简图

国内外学者对RV减速的回差进行了大量研究,吴永宽等[1]对机器人用高精度RV减速机几何回差进行了分析;何卫东与李欣[2]对机器人用高精度RV 传动中摆线轮修形对回差的影响进行了研究。李允宁与蔡胜[3]对 2K-V 型摆线针轮减速机回差与刚度进行了试验研究。Sun与Zhao[4]对RV减速器制造安装误差对回差的影响进行了研究,并用Monte Carlo进行了仿真。王君等[5]建立了摆线针轮齿廓修形的回差精度数值分析模型,并讨论了同一摆线轮齿廓修形方式下不同的修形参数与同一修形参数下不同的修形方式对回差的影响。张迎辉等[6]利用有限元法对RV减速器的回转刚度及回差进行了分析。陆龙生等[7]提出了基于形变量补偿的摆线轮齿廓修形方法,在不改变摆线针轮径向间隙的基础上实现RV 减速器回差的优化。赵大兴等[8]提出了一种改进的滞回曲线法,用于检测RV减速器的回差。张跃明等[9]建立了摆线针轮啮合的力学模型,研究了RV 减速器摆线轮和针轮之间各齿啮合力和回差的变化,结构表明摆线轮的修行方式对机构回差影响较大,摆线轮在运动过程中啮合齿数会有周期性变化。高跃等[10]对RV减速器摆线针轮啮合副中参数的公差带进行了优化,可减小减速器回差;谢雄伟等[11]采用遗传算法对RV减速器零件公差进行了优化,优化后减速器的回差与许用回差接近;蒋淑恋与郑伟峰[12]提出了一种RV减速器回程误差测试方法;陆龙生等[7]对RV 减速器摆线轮齿廓修形方法进行了优化,可以减小减速器回差;张杰等[13]以自制的高精度RV减速器为研究对象,对其参数进行了优化,并对减速器回差进行了分析。

但目前对RV减速器回差的研究都进行了近似,即只考虑了误差大小,并没有考虑误差方向的影响。本文首先建立了RV减速器回差的几何模型,并根据几何模型建立回差的数学模型,并对回差进行仿真,最后利用试验对回差进行了验证。

1 几何模型

本文所研究的RV 型减速机主要由太阳轮、3个行星轮、3 个曲柄轴、2 个摆线轮、针齿、行星架及针齿壳等组成。在进行减速机回差研究时,所采用的几何模型如图2所示。

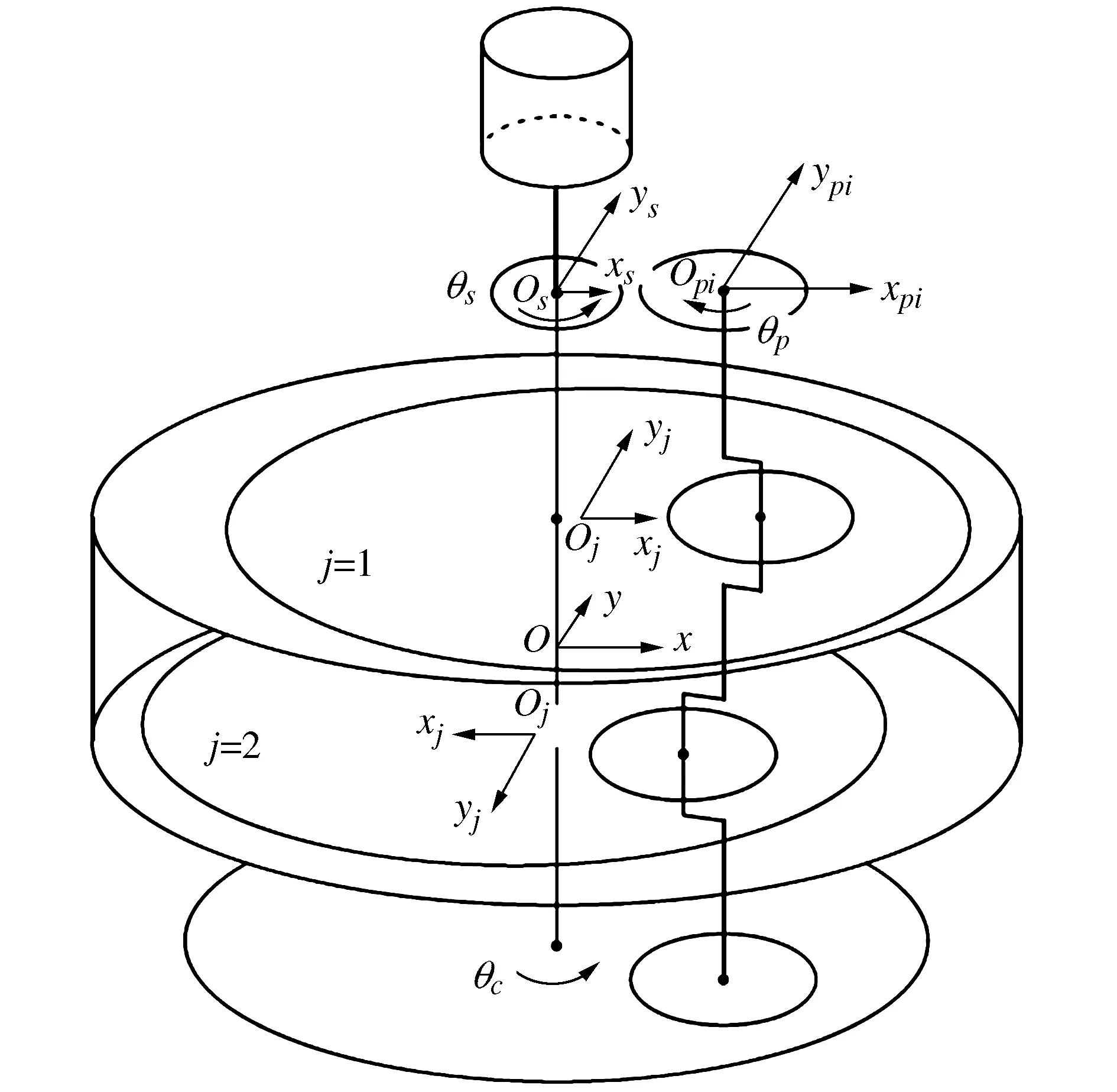
图2 RV传动回差几何模型

图2中各坐标系规定如下:以针轮中心为O原点,垂直其轴线的断面为平面静坐标系(x,y);以太阳轮中心为Os点,建立与太阳轮固连的平面动坐标系(xs,ys);以行星轮中心为Opi点,建立与行星轮固连的平面动坐标系(xpi,ypi);从输入端开始,对两个摆线轮进行编号j=1,2,并以摆线轮的理论质心Oj为原点,以摆线轮的偏心方向为xj轴,沿其逆时针方向转动90°为yj轴,建立摆线轮的动坐标系(xj,yj)。取j=1的摆线轮xj轴及xs,xpi轴在起始位置时与静坐标系x轴方向一致。

2 数学模型

2.1 渐开线齿轮传动部分

渐开线圆柱齿轮传动部分影响回差的主要因素有:1) 中心距误差引起的齿轮侧隙;2)保证补偿制造误差和润滑的啮合间隙及齿形、齿厚偏差引起的齿轮侧隙;3) 齿轮齿圈径向跳动误差引起的齿轮侧隙。

1) 中心距误差引起的回差

(1) 太阳轮中心安装误差

设太阳轮中心安装误差为(Esz,βsz),其中Esz为误差大小,βsz为误差方向,如图3所示。存在误差后，渐开线太阳轮中心由理论的Os点移动到点O′s，太阳轮与行星轮之间的中心距由OsOpi变为O′sOpi。令输入轴(太阳轮)转角为θs，渐开线行星轮的转角为θp。

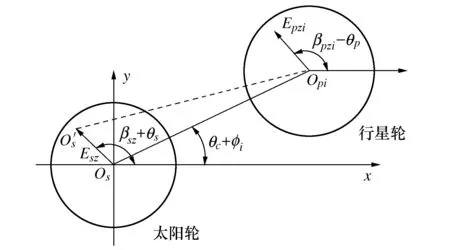
图3 渐开线齿轮传动部分误差模型

当减速器转动时，太阳轮与第i个行星轮的实际中心距为

(1)

式中:i=1,2,3;L为理论中心距;θc为行星轮公转角即行星架转角;φi表示摆线轮(或行星架)上的曲柄轴轴孔的相对位置,φi=2π(i-1)/3,i=1,2,3。

端面齿廓法向侧隙的基本公式[14]为

jbti=eb2-sb1+2(rb1+rb2)invαwti

(2)

式中:rb1,rb2分别为齿轮1,2的基圆半径;αwti为啮合角,满足

(3)

式中:Li为实际工作中心距;eb2为齿轮2的基圆齿槽宽,eb2=e2cosα-2rb2invα;e2为分度圆齿槽宽,e2=πm/2;sb1为齿轮1的基圆齿厚,sb1=s1cosα+2rb1invα;s1为分度圆齿厚,s1=πm/2;α为齿形角,即齿轮分度圆上的压力角。

则端面齿廓圆周方向侧隙为

jwti=jbti/cosαwti

(4)

太阳轮中心安装引起的回差可表示为

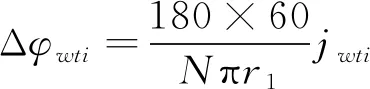
(5)

式中:N为减速器传动比;r1为太阳轮节圆半径。

(2) 行星轮中心安装误差

渐开线齿轮传动部分误差模型如图3所示。

设第i个行星轮中心安装误差为(Epzi,βpzi),其中Epzi为误差大小,βpzi为误差方向, 则太阳轮与行星轮的中心距为

i=1,2,3

(6)

设由行星轮中心距误差引起的圆周侧隙为jwpi。

则行星轮中心安装误差引起的回差为

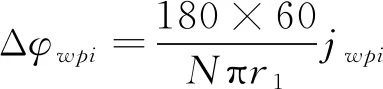
(7)

2) 保证补偿制造误差和润滑的啮合间隙及其他偏差引起的齿轮侧隙。

设太阳轮与行星轮各个轮齿之间的侧隙都近似相等,且圆周方向啮合间隙为jct,引起的回差为

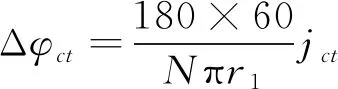
(8)

3) 齿轮齿圈径向跳动误差引起的齿轮侧隙

(1) 设太阳轮齿圈径向跳动误差(Est,βst),存在误差时太阳轮与第i个行星轮的中心距为

i=1,2,3

(9)

设误差引起的侧隙为jsti,则误差引起的回差为

(10)

(2) 行星轮跳动误差(Epti,βpti)

存在误差时太阳轮与第 个行星轮的中心距为

i=1,2,3

(11)

设误差引起的侧隙为jpti,则误差引起的回差为

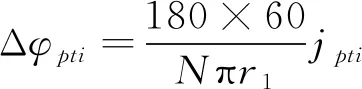
(12)

2.2 摆线齿轮传动部分

1) 针轮齿槽中心圆半径偏差Rk引起的回差

针轮齿槽中心圆半径偏差如图4所示。

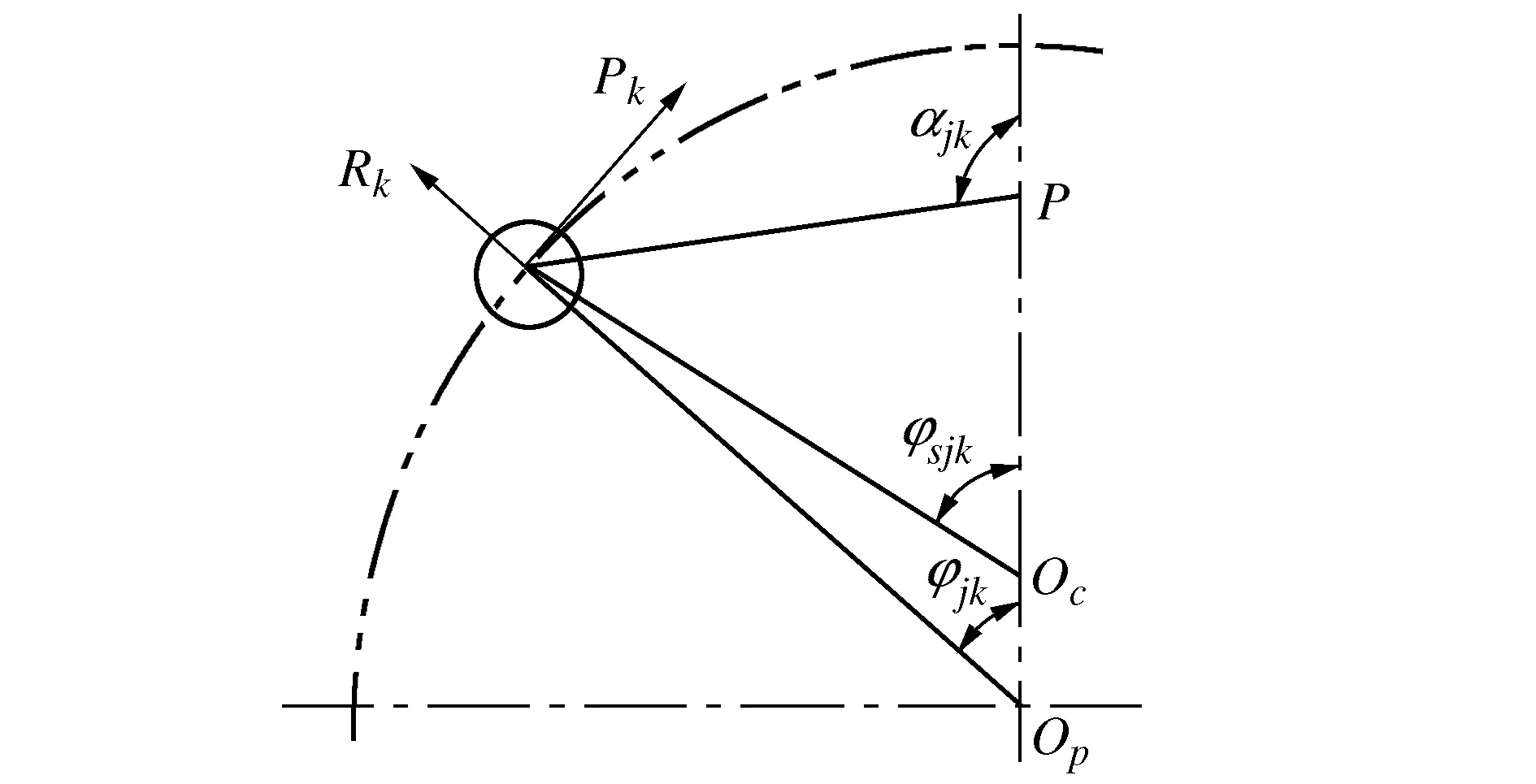
图4 针轮齿槽中误差

图4中:Op为针轮中心，Oc为摆线轮中心，P为节点,φj为两摆线轮的理论质心Oj的相对位置,φj=(j-1)/π,j=1,2。则第k个针齿与摆线轮齿之间的间隙为

eRk=Rkcos(αjk-φjk)

(13)

由第k个针齿引起的减速器回差为

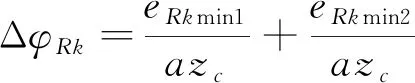
(14)

式中:αjk为第k个针齿中心与第j个摆线轮节点连线与xj轴正方向的夹角;a为曲柄轴偏心距；zc为摆线轮齿数;φjk为第k个针齿半径方向与第j个摆线轮xj轴正方向的夹角;eRkmin1为摆线轮正转时摆线轮与针齿之间的最小间隙;eRkmin2为摆线轮反转时摆线轮与针齿之间的最小间隙。

以下各式中角标为min1和min2均表示摆线轮正转与反转时的最小间隙。

2) 针轮齿槽中心圆周方向位置度偏差Pk引起的回差

由图4可知减速器第k个针齿与摆线轮齿之间的间隙为

ePk=Pksin(αjk-φjk)

(15)

则引起的回差为

(16)

3) 针轮齿槽半径误差Ck引起的摆线轮回差

针齿齿槽半径误差,造成针齿在啮合点法线方向方向的移动距离为Ck,则

引起的回差为

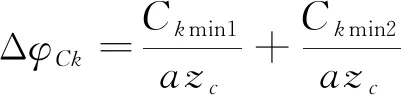
(17)

4) 针齿半径误差Gk引起的摆线轮回差

针齿半径误差为Gk,则引起的回差为

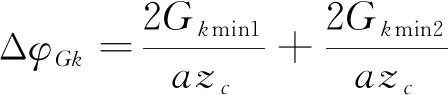
(18)

5) 摆线轮修形引起的回差

设修形滚子半径的变化值为Xk,摆线轮上每个啮合点处的Xk都不相同。

引起的回差为

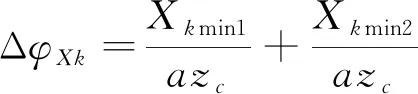
(19)

6) 成形砂轮进刀深误差Sk

采用成形砂轮加工摆线轮时,由于砂轮进刀深误差,使得摆线轮齿形产生误差,造成回差。

进刀深误差引起的间隙为

eSk=Skcos(αjk-φSjk)

(20)

式中:φSjk为第k个针齿中心与第j个摆线轮中心连线与轴正方向的夹角。

引起的回差为

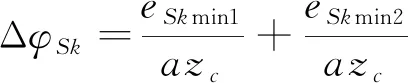
(21)

7) 分度盘分度误差Fk引起的回差

采用成形砂轮加工摆线轮时,每磨削完一个齿,机床分度机构带动摆线轮转过一个齿距角,磨削下一个齿,由于机床分度误差,造成摆线轮齿存在误差。

误差引起的间隙为

eFk=Fksin(αjk-φSjk)

(22)

引起的回差为

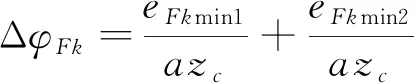
(23)

8) 摆线轮齿圈径向跳动引起的回差

设误差为(Ebtj,βbtj),则在每个齿处引起的间隙为

ebtjk=-Ebtjkcos[φSjk-(βbtj+θc)]cos(αjk-φSjk)

(24)

引起的回差为

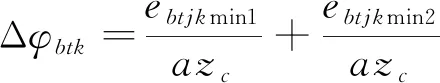
(25)

9) 摆线轮曲柄轴孔的偏心误差

与摆线轮齿圈径向跳动误差类似,设误差为(Ehj,βhj),造成的间隙

ehjk=-Ehjicos[φSjk-(βhj+θc)]cos(αjk-φSjk)

(26)

引起的回差为

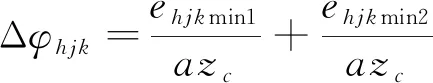
(27)

2.3 曲柄轴偏心凸轮的偏心误差造成的回差

设误差为(Ecj,βcj),与曲柄轴孔的偏心误差类似,造成的间隙为

ecjk=-Ecjcos[φSjk-(βcj+θp)]cos(αjk-φSjk)

(28)

引起的回差为

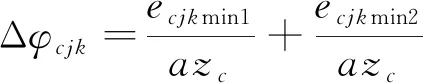
(29)

2.4 行星架上曲柄轴孔的偏心误差及行星架的装配误差引起的回差

行星架上曲柄轴孔的偏心误差(Ea,βa)及行星架的装配误差(Ec,βc)造成的回差与式(28)一致,计算时,只需要将式(28)中的误差角标替换即可。

2.5 摆线轮曲柄轴孔轴承间隙对回差的影响

转臂轴承存在的游隙会对回差产生影响,设间隙为u,偏心距为a,为消除间隙,偏心轴需转动Δθpi角度,则

(30)

由于

(31)

则引起的回差为

Δφqi=2×Δθci

(32)

3 RV减速器回差仿真

本文选择RV减速器参数如表1所示,表2为RV减速器各零件尺寸公差,假设减速器所有零件的制造及安装误差均在公差值范围内。

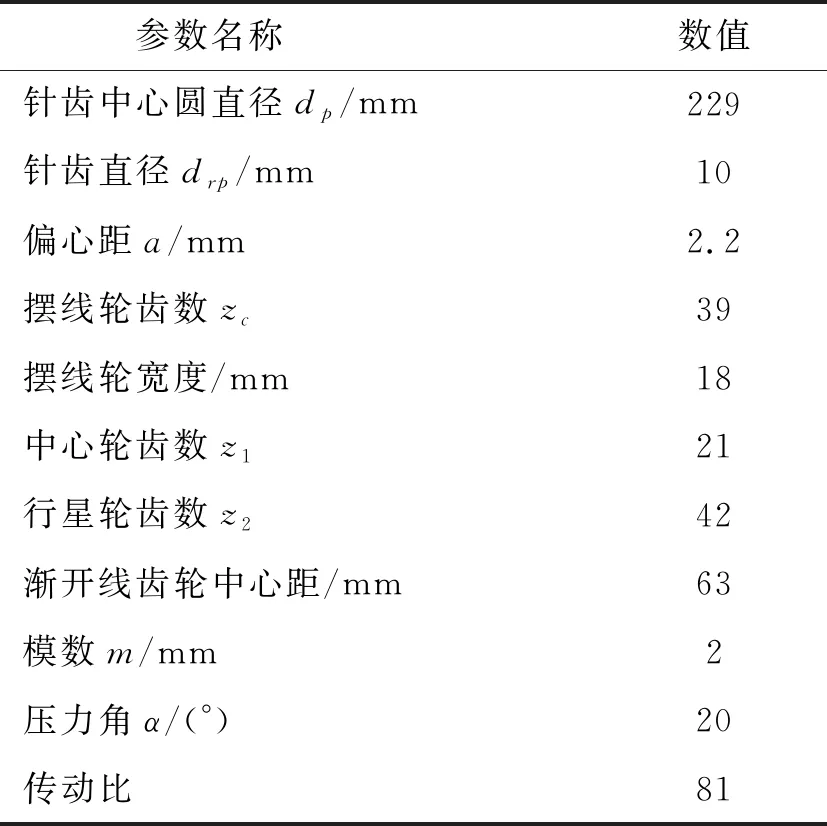
表1 减速器参数

表2 制造及安装误差误差

当取太阳轮中心安装误差值Esz=8 μm,误差方向分别为βsz=0、βsz=70°和βsz=140°,根据式(2)计算出的由太阳轮中心安装误差引起的减速器回差如图5所示。

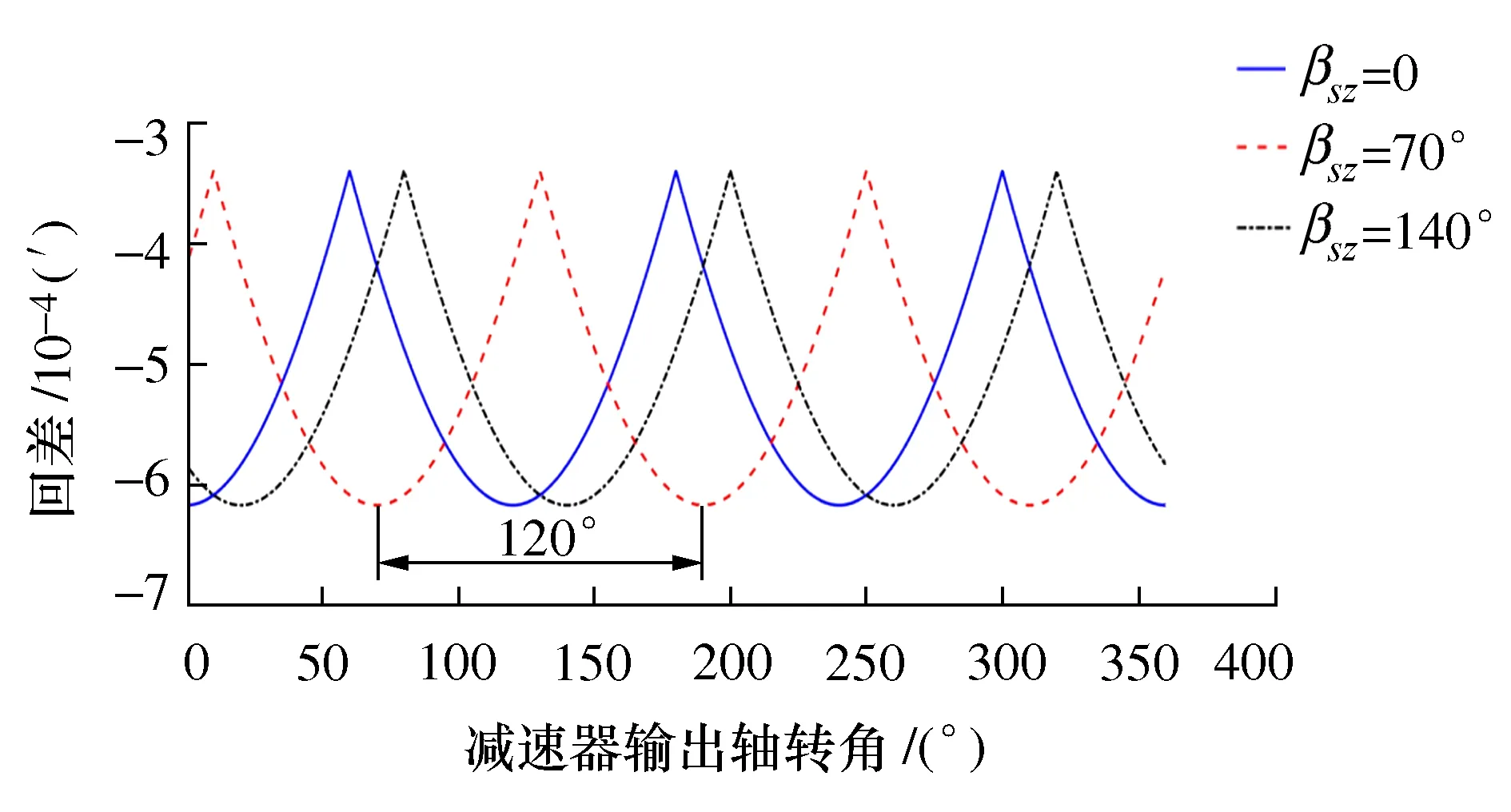
图5 太阳轮中心安装误差引起的回差

图5包含3条回差曲线,分别对应3个不同的误差方向。从图中可以得出:当减速器输出轴处于不同相位时,不同误差方向引起的回差各不相同,但太阳轮中心安装误差方向只改变了回差的初始相位,不影响回差的幅值;由于渐开线齿轮处于第一级减速部分,受传动比影响,太阳轮中心安装误差引起的减速器回差较小;由于RV减速器有3个行星轮,在减速器输出轴回转一周,回差有3个明显的波峰,同一波形两个峰值之间相位角相差120°。

选取太阳轮齿圈径向跳动误差值Est=11 μm,误差方向分别为βst=0、βst=70°和βst=140°。则根据式(5)计算出的减速器回差如图6所示。在图6中:由于太阳轮每转动一圈便与3个行星轮啮合,啮合频率较高,所以太阳轮齿圈径向跳动误差引起的回差周期较小,图6中仅列出了输出轴旋转9°的回差;与太阳轮中心安装误差类似,太阳轮齿圈径向跳动误差方向不同时,回差的初始相位不同,但回差幅值相同;虽然回差波峰与波谷相差较大,但对减速器整体回差影响较小。

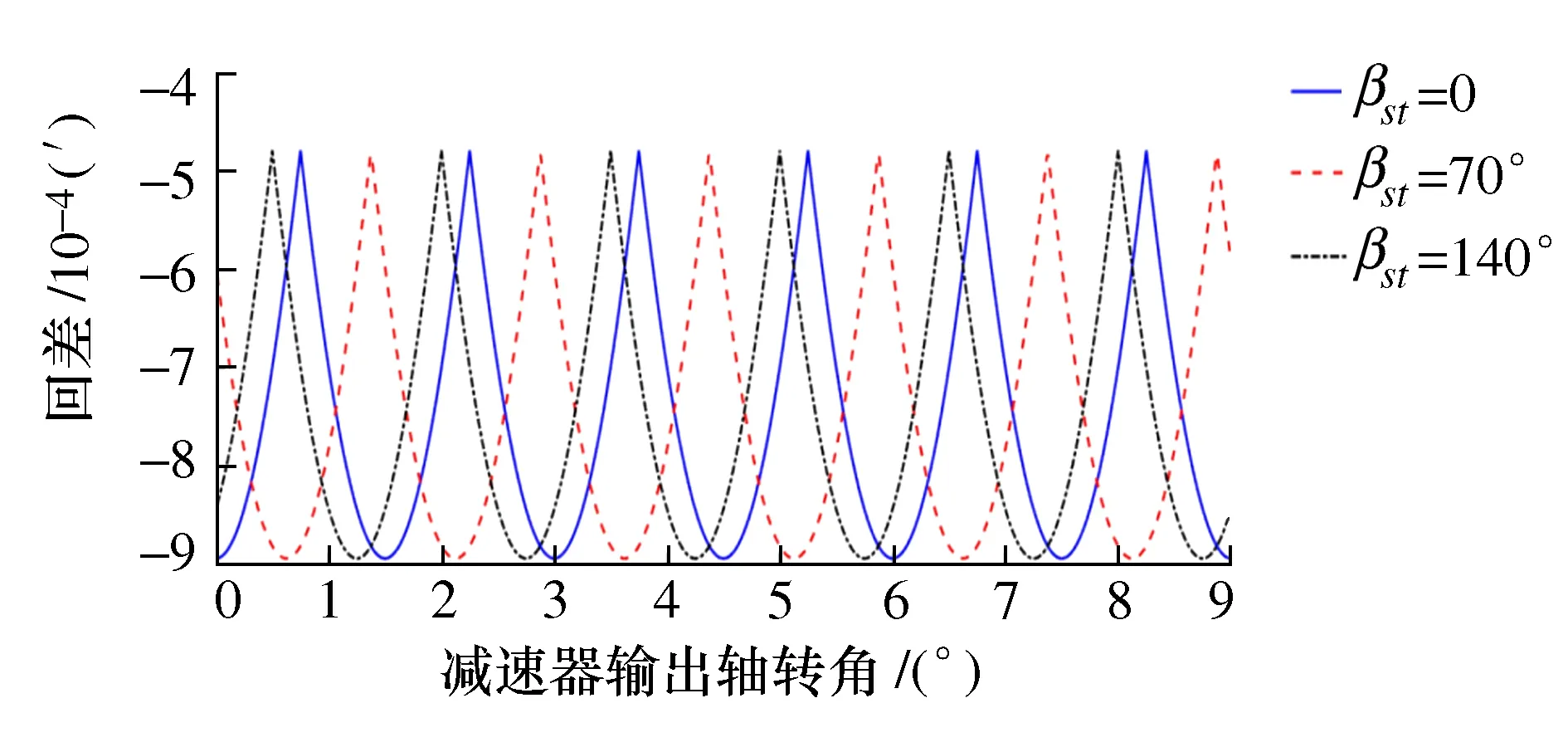
图6 太阳轮齿圈径向跳动误差引起的回差

选取针轮齿槽中心圆半径误差值Rk=3 μm,根据式(7)计算出的减速器回差如图7所示。图中回差峰峰值相差较小,但也呈周期性变化。由于摆线针轮传动机构处于减速器传动链的末端,所以误差引起的回差较大。

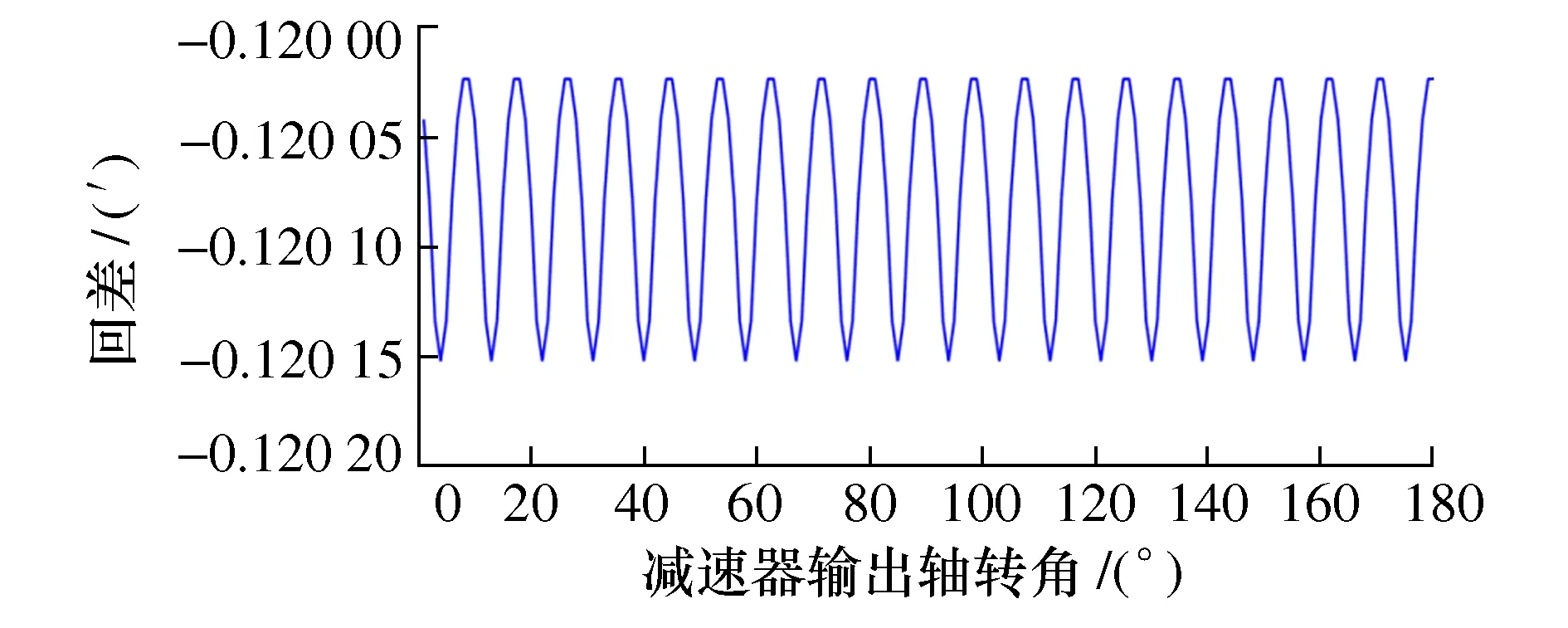
图7 针轮齿槽中心圆半径误差引起的回差

选取摆线轮齿圈径向跳动误差值Ebt=6 μm,误差方向分别为βbt=0、βbt=70°和βbt=140°,则根据式(23)计算出的减速器回差如图8所示。在图8中:误差方向只改变了回差的初始相位,并不改变回差的幅值。

图8 摆线轮齿圈径向跳动引起的回差

选取摆线轮齿廓修形方法为等距加移距修形(其中等距修形量为-0.026 mm,移距修形量为-0.03 mm);选取表2所示各零件公差的均值作为各零件实际误差值,误差方向随机选取,则RV减速器回差如图9所示。当所有误差方向均为零度时,减速器回差如图10所示。

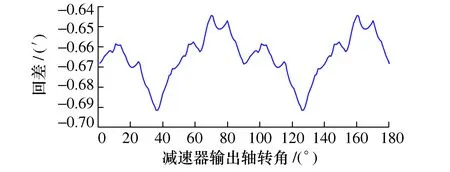
图9 RV减速器回差

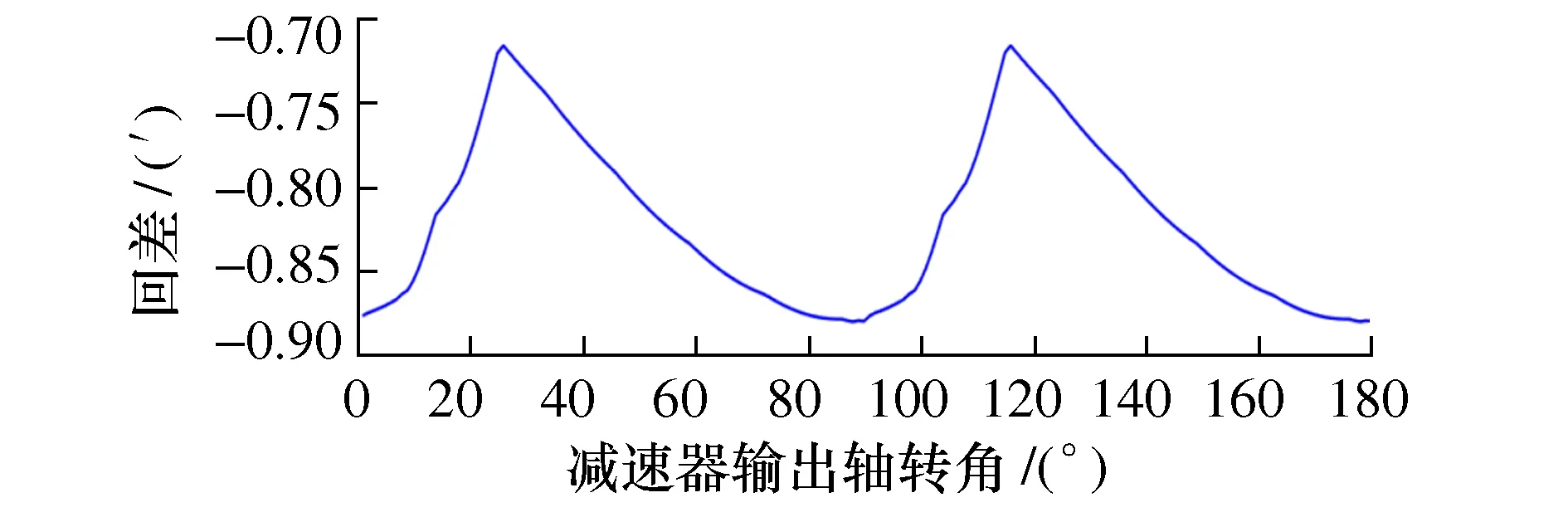
图10 误差方向为零度时的RV减速器回差

图9显示:误差引起的减速器回差具有周期性,回差值在减速器输出轴不同相位各不相同;由于选择最小修形间隙为零,图中回差为负值,最小值为-0.691′;回差最大值与最小值(峰峰值)之差为0.046′。

图10显示:当误差方向相同时,减速器回差最小值为-0.875′,回差最大值与最小值(峰峰值)之差为0.16′。

从图5～图10所示回差的分析中可以得出:单项误差的方向只影响回差的初始相位,不影响回差幅值;所有误差方向相同时,回差绝对值及峰峰值都显著增加。实际中,可通过控制影响回差较大的误差来减小回差;在已知各零件误差方向的情况下,也可以通过选配减速器零件,避免各零件引起的减速器回差的峰峰值叠加,以减小回差。

4 RV减速器回差试验

回差试验选用秦川机床集团有限公司的RV减速器试验台,如图11所示。该试验台由伺服电机、台架、减速器及光栅编码器组成,试验台电动机的旋转角度可精确控制。在减速器输出轴上安装有光栅编码器,可精确的测量减速器输出轴的角位移。试验台可完成RV减速器的传动误差及回差试验。本次测量回差试验用减速器型号为:BX320,该减速器为秦川机床集团RV减速器厂生产,如图12所示,减速器传动比为201,额定扭矩3 150 Nm。

图11 RV减速器回差试验台

图12 试验用RV减速器

RV减速器回差测量有两种方案:1) 固定减速器输入轴,测量输出轴在零转矩时或微小转矩时的最大回转角,该角度即为减速器回差;2) 由电机带动减速器输入轴转动,测量输入轴顺时针与逆时针旋转时输出轴在零转矩时或微小转矩时的旋转角度滞后量,即回差。采用第1种测量方案测量减速器回差时,需要多次调整减速器输入轴的相位角以获得输出轴的相位角,但输入轴的相位角不易精确定位。本文测量回差采用第2种试验方案,即由电机精确控制输入轴相位角,获得输出轴在不同相位时的回差。

由于RV减速器输出轴在不同相位时的回差不同,本文选择若干相位角进行测量,测量相位角数目越多,则测量结果越精确。在图11所示试验台中,根据减速器传动比,控制伺服电机输出转角,使减速器输出轴旋转至待测量相位角,然后使电机反转一定角度,则输出轴理论转角与实际转角之差即为待测量相位角处的回差。重复上述测量步骤,即可完成减速器输出轴在所有待测量相位角处的回差。本文选择同一型号的两个减速器进行测量,并将测量获得的两个减速器的回差计入表3,绘制回差曲线如图13所示。

表3 RV减速器实测回差数据

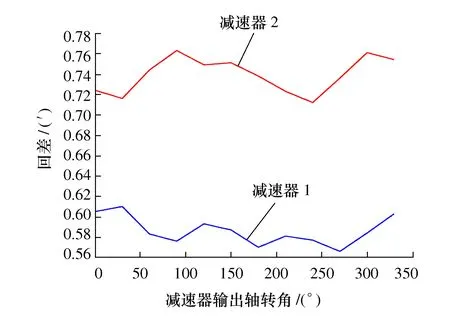
图13 RV减速器实测回差

表3所示回差值中,每两个测量位置减速器输出轴的相位角间隔30°。图13回差曲线结果显示RV减速器输出轴在不同相位时的回差均不同。其中,减速器1的最大回差为0.61′,最小回差为0.566′,回差最大值与最小值之差为0.044′;减速器2的最大回差为0.763′,最小回差为0.712′,回差最大值与最小值之差为0.051′。

图13中实测减速器回差的峰峰值之差与图9仿真结果基本一致,由于回差试验只测量了减速器输出轴在部分相位时的回差,图13中非测量点的回差由插值获得。回差试验证实RV减速器回差具有周期性。对于精密摆线针轮传动,应精确计算回差,减小摆线针轮传动机构传动误差。

5 结论

本文综合考虑了RV减速器各零件制造及安装误差的大小及方向,建立了RV减速器回差的几何模型及数学模型。并对各种误差引起的减速器回差进行仿真,获得了单项误差及多种误差引起的RV减速器回差,从中得出:在减速器的一个回转周期内,摆线轮不同相位时的回差并不相同,单项误差方向只改变了回差的初始相位,不影响回差的幅值;当误差方向随机选取时,峰峰值之差约为回差均值的10%;所有误差方向相同时,回差绝对值及峰峰值都显著增加。最后通过回差试验证实了理论分析的正确性。本文研究结果为RV减速器零件的公差设计提供理论依据,同时研究方法可用于其他结构形式的摆线针轮行星传动回差的研究。