一种非均匀噪声条件下基于子空间的实值DOA估计方法

何 莉，朱扬辉，唐 龙

(长海发展有限责任公司,广西 桂林 541000)

0 引 言

波达方向(DOA)估计是阵列信号处理领域的一个重要研究课题，已广泛应用于各种场景，如无线通信、雷达、声纳、导航、地震探测和医学等。经典的DOA估计算法包括：多重信号分类算法(MUSIC)、信号参数估计旋转不变技术(ESPRIT)和最大似然(ML)估计算法等。这些方法可以获得较高的角度分辨率，实际应用广泛。但其均是在均匀白噪声的条件下提出的，当噪声是非均匀噪声时，由于不正确的噪声模型会导致基于均匀白噪声假设下的传统 DOA 估计算法性能显著下降。

在实际中，由于接收通道硬件不理想及外界影响，各传感器中的噪声可能为不相关的非均匀高斯白噪声。近年来，针对非均匀噪声下的DOA估计问题，研究学者提出诸多新颖的方法。在文献[5]中，一种非均匀噪声条件下的ML 估计算法被提出，通过迭代方法求解角度估计。但由于对初始值的设置较严格，并且计算量巨大，从而限制了该算法的实际工程应用。文献[6]提出了2个基于子空间的DOA 估计方法，通过利用ML 和最小二乘(LS)技术循环迭代的方法来估计信号和噪声子空间，以此获得DOA估计。该算法同样需要预设初始值，并且随着迭代次数的增加，该算法也相当耗时。由于核范数最小作为非凸优化问题秩最小问题的最优凸松弛，而被广泛地应用到解决秩最小问题，并且有学者已将该技术成功应用于非均匀噪声条件下的DOA估计中。文献[7]提出了一种基于子空间无迭代(NB)DOA估计算法，该方法通过对阵列协方差矩阵进行特殊分解后，再经过2次特征值分解后，便可消除非均匀噪声的干扰，无需迭代和凸优化过程。然而，由于其需要对复值协方差矩阵进行特征值分解，仍然具有一定的计算复杂度。

针对复值协方差矩阵特征值分解计算复杂度高的问题，酉变换技术已被应用到诸多DOA估计算法中。在文献[8]中，实值MUSIC算法被提出。该算法利用center-Hermitian矩阵性质，将复值协方差矩阵转换为实值协方差矩阵。对该矩阵进行特征值分解和空间谱搜索时，仅需要考虑实值。相似地，文献[9]提出了实值ESPRIT算法，该算法可以提供更低的计算复杂度。然而，由于酉变换技术使用了前后向平滑技术，可能会导致估计性能下降，因此文献[10]提出实值求根MUSIC算法，该算法没有出现这种性能下降。上述基于酉变换技术的DOA估计方法可以有效降低计算复杂度，同时提供较好的DOA估计性能。

考虑到非均匀噪声下DOA估计算法存在的问题以及酉变换技术的优点，本文在非均匀噪声背景下利用基于子空间无迭代方法和酉变换技术，提出一种基于子空间的实值DOA估计方法，以改善非均匀噪声条件下DOA估计性能。该方法首先利用酉变换技术将阵列协方差矩阵转换为实值协方差矩阵，以提高计算效率；然后对实值协方差矩阵进行特殊分解，并构造特定向量获得实值噪声协方差矩阵，以消除非均匀噪声的干扰；最后，对实值协方差矩阵和实值噪声协方差矩阵进行广义特征分解估计噪声子空间，并利用传统的实值MUSIC算法获得最终的DOA估计。该算法无需迭代和凸优化过程，可以以较低的计算复杂度获得高分辨的DOA估计结果。

1 信号模型

考虑一个包含有个阵元的均匀线阵，相邻阵元之间的间距为=2，其中表示信号波长。假设有个远场窄带信号，从方向,,…,入射到阵列上，接收信号矢量可以表示为：

()=()+()

(1)

通过收集次采样快拍，式(1)可以改写为：

=+

(2)

由此，阵列协方差矩阵可以表示为：

={()()}=+

(3)

(4)

2 算法描述

在基于子空间的DOA估计算法中，需要首先估计噪声协方差矩阵，然后利用噪声子空间和导向矢量的正交特性来估计DOA。提出的方法首先利用酉变换技术将复值协方差矩阵实值化，以有效降低计算复杂度。

众所周知，如果一个矩阵是centro-Hermitian矩阵，那么其满足：

=

(5)

式中：表示×维的交换矩阵，其副对角线元素等于1，其他为0。

那么，矩阵可以转化为一个实值对称矩阵：

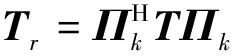
(6)

式中：表示酉矩阵，其奇数阶和偶数阶可以分别表示为：

(7)

(8)

式中：表示×维的单位矩阵；表示×维的全矩阵。

值得一提的是，对实值对称矩阵进行特征值分解时，仅需要考虑实数，即没有复数的乘法运算。然而，由于式()中的噪声协方差矩阵是非均匀的，每一个阵元上的噪声功率互不相等。因此，只是一个Hermitian矩阵，并不是一个对称矩阵。根据文献[]，对执行对称估计，能够近似转变为一个centroHermitian矩阵，具体转换如下：

()

式中：是在欧氏距离意义下的的最优Hermitian对称估计；[·]表示共轭。

因此，实值阵列协方差矩阵可以表示为：

()

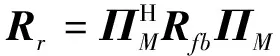
将式()和式()代入式()后，可以得到：

()

()

()

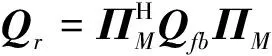
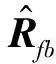
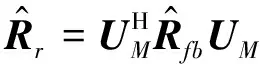
至此便完成酉变换的转换，得到实值阵列协方差矩阵。接下来，将对矩阵进行分解，以消除非均匀噪声的影响。

通过观察，阵列协方差矩阵可以分解成个矩阵之和，如下所示：

rr

()

式中：

()

()

式中：表示第个信号的信号功率；矩阵r的对角线上元素等于，非对角线上元素等于矩阵；矩阵r是一个对角矩阵，其对角线上元素等于矩阵对角线上的元素。

根据子空间算法可知，()是一个×满秩的矩阵，其MP维正交矢量(i,…,MP)应满足如下等式：

()

(17)

又根据文献[8]可知，实值的可以通过下式获得：

(18)

将式(11)两边同乘，并且利用式(17)和式(18)，可得：

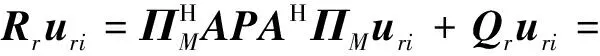
，=1,…,-

(19)

通过式(19)可知，正交矢量(=1,…,-)是由矩阵和矩阵进行广义特征值分解后张成的噪声子空间。然而，由于矩阵是未知的，正交矢量(=1,…,-)在非均匀噪声条件下，不能够直接获得。

将式(14)带入式(19)，可得：

(20)

首先，将实值噪声协方差矩阵分解成2个对角矩阵：

=+

(21)

式中：表示为稍后计算的传感器噪声功率的公共部分；为对角矩阵，其对角元素除一个元素等于0外，其余元素均为非零元素，并且这个零元素的位置就是矩阵的对角元素中最小元素所对应的位置。

此外，构造一个-1维单位矢量，满足：

(22)

式中：的值等于diag()最小值的位置下标，即满足:

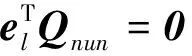
(23)

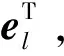
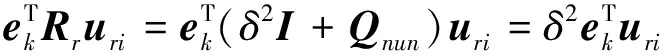
(24)

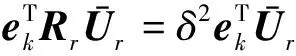
(25)

因此，可以计算为:

(26)

式中:|·|表示绝对值运算符。

那么，矩阵可以通过下式获得:

=diag{[]-,…,[],-}

(27)

式中:表示矩阵中的对角元素中最小对角元素的值。

利用式(21)可以获得矩阵。最后，根据文献[7]对矩阵和矩阵进行广义特征值分解，可以获得更加精确的噪声子空间。

当获得噪声子空间后，便可以利用传统的实值MUSIC算法通过搜索空间谱估计个信号的DOA：

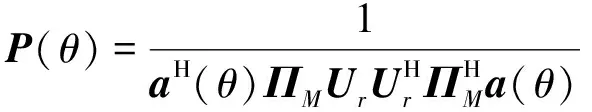
(28)

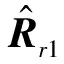
3 仿真分析

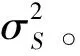
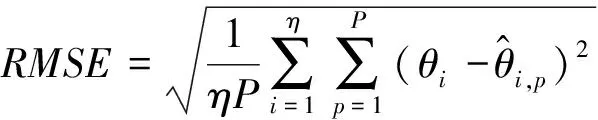
(29)

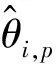
图1展示了MUSIC算法和所提算法的空间谱。在本次试验中，假设信噪比=0 dB，采样快拍数=500。从图中可以看出，MUSIC算法由于受非均匀噪声的干扰，会导致分辨率降低，已经无法分辨出2个角度相邻较近的目标。这也证明了非均匀噪声对于传统的角度估计算法具有影响，会导致估计性能显著下降。然而本文所提出的算法利用2次特征值分解，可以估计出噪声协方差矩阵，能够正确分辨出3个目标角度。

图1 空间谱

图2为展示了4种方法和克拉美罗界(CRB)获得的均方根误差随信噪比变化的关系图，其中，假设采样快拍数=100。由图 2可知，当<0 dB时，NB算法比MUSIC算法具有更好的估计性能，这是因为NB算法消除了非均匀噪声的干扰。而后，由于快拍数较小的原因，MUSIC算法的估计精度优于NB算法。随着信噪比的增加，噪声功率逐渐降低，4种算法DOA估计的RMSE均逐渐降低。此外，所提出的方法在整个信噪比变化范围内总是保持比其他方法优秀的性能。

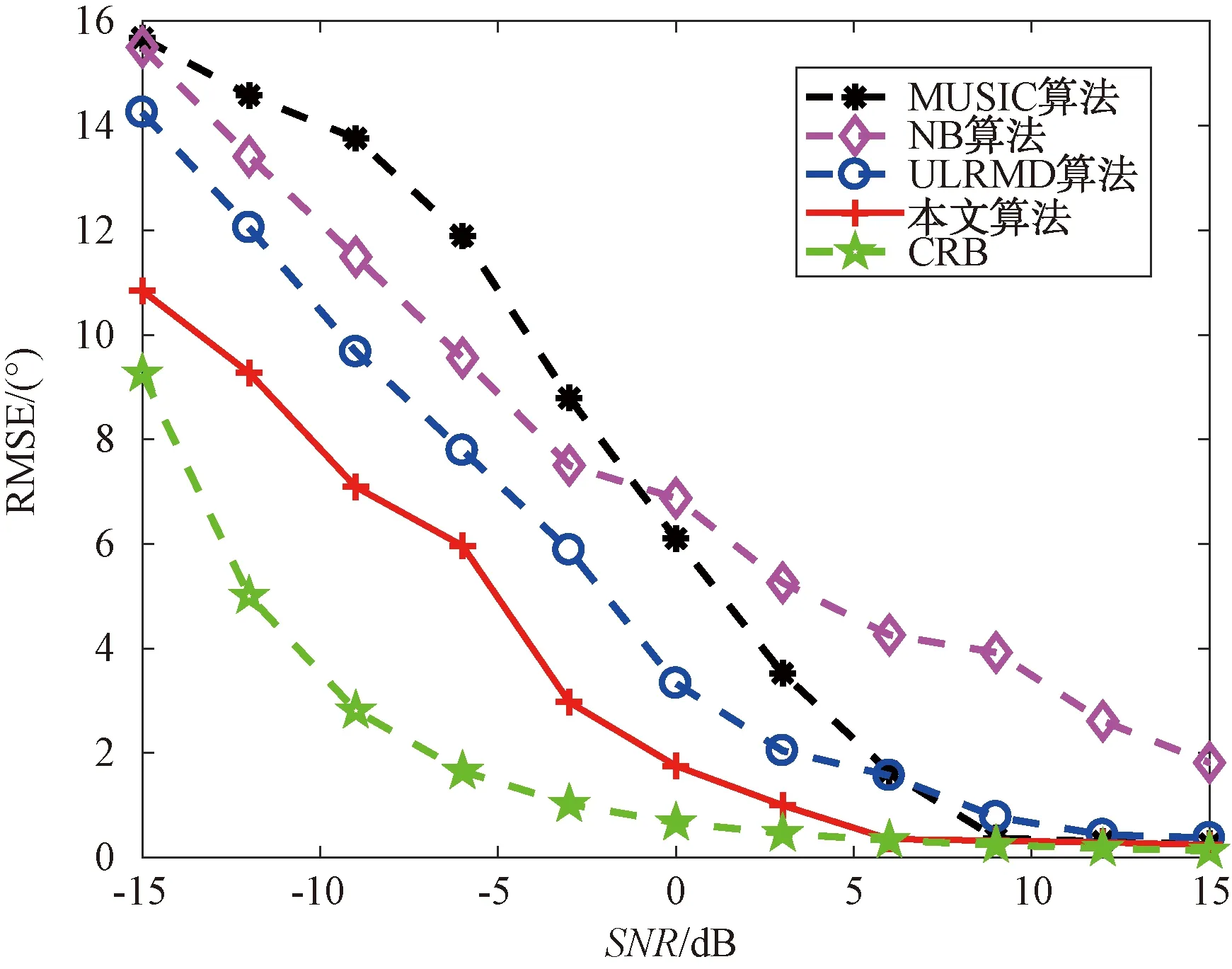
图2 均方根误差随信噪比变化的关系图

图3展示了4种方法和克拉美罗界获得的均方根误差随采样快拍数变换的关系图。其中，假设=10 dB。在大信噪比条件下，非均匀噪声的干扰已经不再是影响DOA估计性能的主要因素，故MUSIC算法优于NB算法和ULRMD算法。从图 3可以看出，NB算法在快拍数较小的条件下，DOA估计精度显著下降。ULRMD算法和所提的算法由于使用的酉变换技术，加倍快拍数，使得DOA估计精度优于NB算法。ULRMD算法由于使用低秩矩阵完备技术，需要较大的快拍数来恢复低秩矩阵，在快拍数较小的情况下，估计精度低，故MUSIC算法的估计精度优于ULRMD算法。然而，所提出的算法在整个快拍数变化范围内，所提算法具有优于其他算法的DOA估计性能。

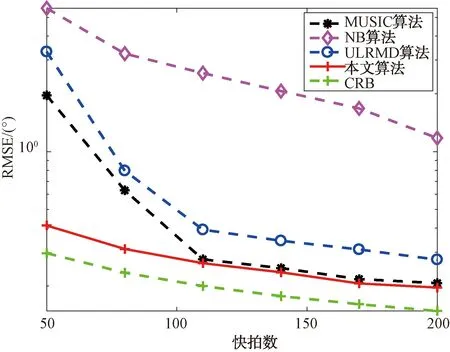
图3 均方根误差随采样快拍数变化的关系图

图4展示了通过不同方法在相关源条件下获得DOA估计的结果。其中，假设信噪比=5 dB，采样快拍数=100。本次实验假设有=2个相干源，分别为=-10°,=0°。从图 4可以看出，MUSIC算法和NB算法无法分辨出相干信号，然而ULRMD算法和所提出的算法可以分辨出相干信号。这是由于ULRMD算法和所提算法在酉变换技术中，利用了前后向平滑技术，故可以解相干，具备一定的解相干能力。

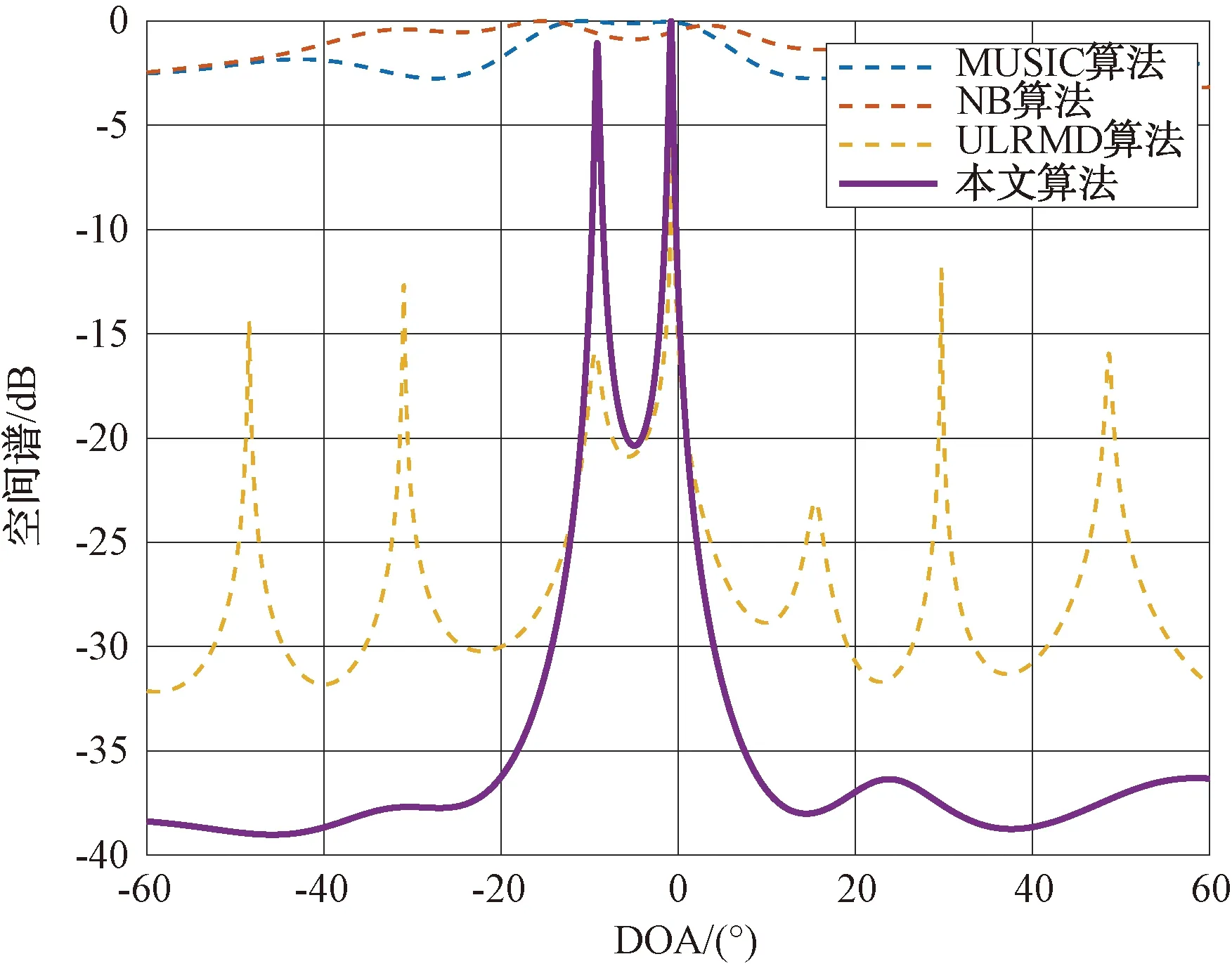
图4 相干源的空间谱

图5展示了所提出的方法和ULRMD方法之间的仿真时间比较。其中，假设=0 dB和=100 。从图 5可以看出，ULRMD算法由于需要凸优化过程，故相比于所提算法需要更多的计算时间。所提算法可以在0.1 s内实现DOA估计，具有一定的实际应用价值。

图5 仿真时间比较

4 结束语

针对非均匀噪声条件下DOA估计问题，本文提出一种基于子空间的实值DOA估计方法，并通过仿真试验进行验证。在不同信噪比和不同快拍数条件下，将所提算法与MUSIC算法、NB算法和ULRMD算法进行比较。试验结果表明，该算法能够有效抑制非均匀噪声的干扰，提供较好的DOA估计性能。

与NB算法和ULRMD算法相比，所提算法结合酉变换技术，无需迭代或凸优化过程便可以消除非均匀噪声的影响，具有更高的分辨率和更低的计算复杂度，并且还具有一定的解相干能力和工程价值。