多无人机对组网雷达的协同欺骗干扰技术

刘宇蕊，束 坤，李 迪

(中国船舶集团有限公司第八研究院，江苏 扬州 225101)

0 引 言

在现代信息化对抗环境中，组网雷达系统因其较好的“四抗”特性在军事上得到了广泛的应用，如何对组网雷达进行有效的欺骗干扰成为了当前雷达对抗领域亟待解决的问题。无人机作为新型作战平台，能携带载荷对雷达进行欺骗干扰，但单架无人机的欺骗效果已无法满足作战需要，因此本文采用多无人机协同的方式产生一条预先设计好的虚假航迹，实现对组网雷达的航迹欺骗干扰。对于给定的虚假航迹，利用无人机、雷达、假目标三者的位置关系求解得到综合考虑无人机数量、航迹坐标以及运动参数的最佳方案，完成航迹欺骗的同时也满足了无人机的动力学约束，具有一定的参考价值。

1 多无人机对组网雷达协同欺骗干扰原理

无人机上携带的干扰载荷使用数字射频存储技术(DRFM)，能够存储、延迟转发以及放大欺骗干扰信号，使雷达能接收到一个或多个位于无人机与雷达连线上的、比真实目标靠后的回波信号。在组网雷达系统中，真实目标与有源虚假目标在空间状态上存在显著差异：在统一坐标系中，各雷达站测量的真实目标空间状态是相同的，认为具有“同源性”；不同雷达测量的虚假目标的空间状态不一致，认为具有“非同源性”。利用组网雷达真假目标空间状态差异来识别虚假目标的方法被称为“同源检验”，组网雷达系统信息融合中心基于一定的“同源检验”融合规则，对接收到的多部雷达在统一坐标系的同一空间位置上检测到的目标信号，判断其是否为一个合理的目标航迹点，多个连续的合理目标航迹点就形成了目标航迹。图1为多无人机协同对组网雷达进行航迹欺骗的示意图。

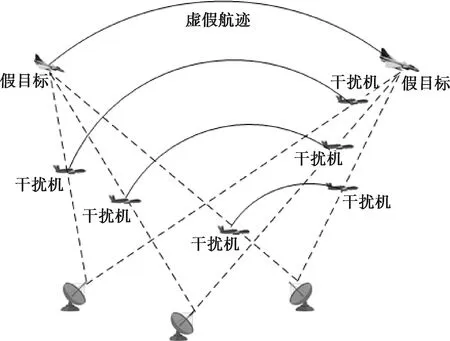
图1 多无人机协同对组网雷达航迹欺骗示意图

2 多无人机协同欺骗干扰模型的建立

2.1 模型假设

假设一：无人机具备较强隐身能力，不易被组网雷达检测到，并且同一时刻1架无人机只能干扰1部雷达。

假设二：无人机的飞行速度、飞行高度、最大加速度、转弯半径以及无人机间距均控制在合理的范围内。

假设三：组网雷达系统由5部雷达组成，雷达最大作用距离均为150 km，并且该组网雷达系统每部雷达的数据更新率为10 s。

假设四：至少需要有3部雷达的航迹点状态信息通过了“同源检验”，组网雷达系统才将其确定为一个合理的航迹点，20个连续的经信息融合中心确认的航迹点形成的合理航迹，将被组网雷达系统视为一条真实的目标航迹。

2.2 单机欺骗干扰单部雷达数学模型

图2为单架无人机对单部雷达进行航迹欺骗干扰的位置关系示意图。其中(，，)、、、分别代表假目标的位置坐标、速度、航迹倾角以及航迹偏角。(，，)、、、分别代表欺骗干扰无人机的位置坐标、速度、航迹倾角以及航迹偏角。(，，)代表雷达的位置坐标，、分别代表雷达与假目标以及无人机的距离，、分别代表雷达与假目标连线的方位角以及俯仰角。

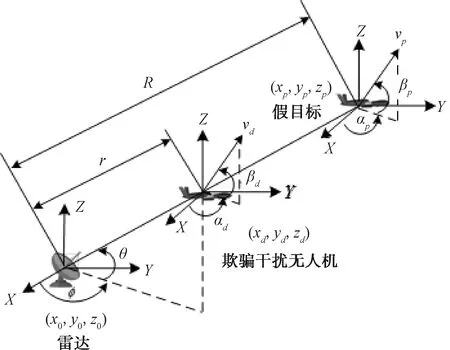
图2 单架无人机欺骗干扰单部雷达位置关系示意图

在直角坐标系中，假目标的运动学方程是：

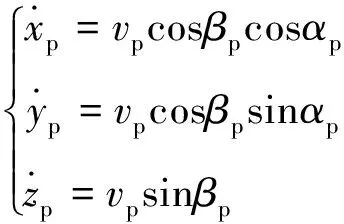
(1)

在球坐标体系中(原点和雷达位置重合)，假目标的位置满足：

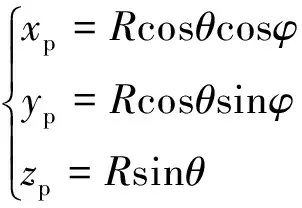
(2)

对式(2)求导并转化为矩阵形式，可以得到：

(3)

联立式(1)和式(3)，经过整理后有：

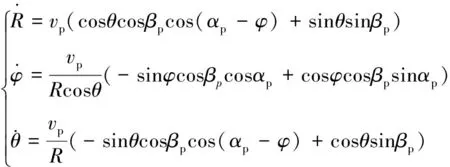
(4)

同理，欺骗干扰无人机的运动状态应满足：

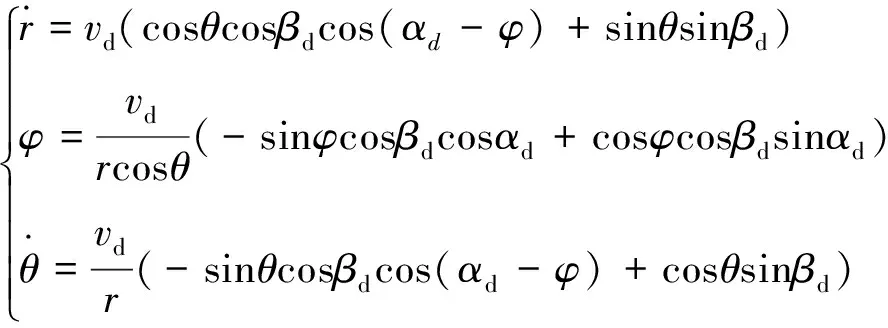
(5)

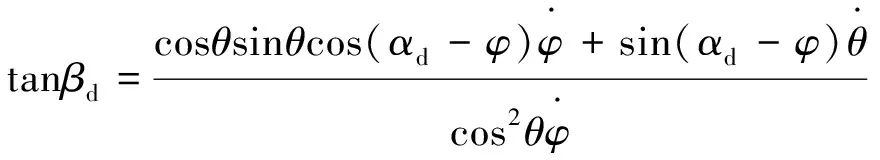
(6)

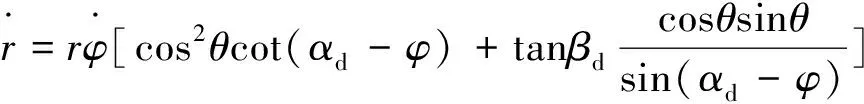
(7)

且欺骗干扰无人机的速度计算公式为：

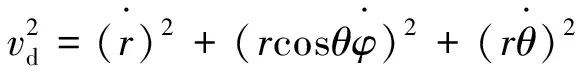
(8)

综上所述，式(1)～式(7)即为单架无人机欺骗干扰单部雷达的数学模型。

2.3 多无人机协同欺骗最优控制模型

设假目标航迹中的任意一个假目标点与任意一部雷达的连线上有一架无人机，则记为=1，反之则记为=0。考虑无人机的飞行速度、高度、转弯半径，无人机间距以及组网雷达系统“同源检测”规则，对多无人机协同欺骗最优控制模型进行约束，约束条件如下：

(1) 无人机飞行速度满足：120≤≤180(速度单位为km/h)；

(2) 无人机飞行高度满足：2 000≤≤2 500(高度单位为m)；

(4) 设无人机的转弯半径≥250；

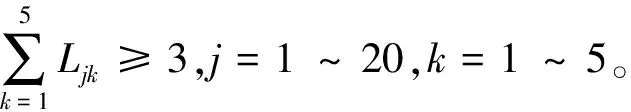
综上所述，为了产生1条预设的假目标航迹，采用多机协同的方式进行欺骗干扰，所需无人机的最小数量满足如下优化模型：

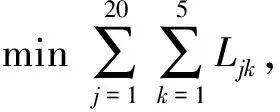
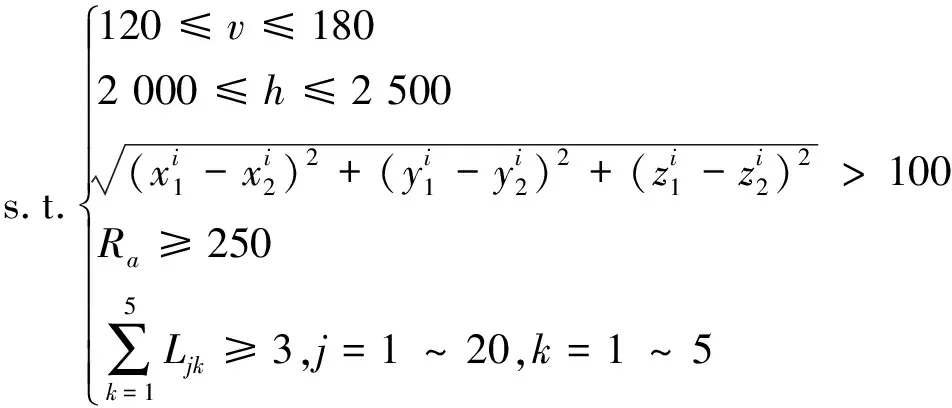
(9)

3 多无人机协同欺骗干扰模型的求解

考虑组网雷达系统的“同源检验”规则，若要产生1条预先设计好的假目标航迹，理论上至少需要3架无人机，则可考虑安排3架无人机分别对3部雷达进行干扰，现假定安排无人机，，分别干扰雷达，，，且每一架无人机在～时刻只对1部雷达进行干扰。

如图3所示，、为假目标航迹上相邻时间的虚假点，设无人机在、时刻的坐标分别为：-(,,)、-(,,)，其中无人机在时刻位于直线上，在时刻位于直线上，当无人机飞行高度固定后，无人机坐标可由雷达、无人机、虚假目标点三者的几何位置关系确定。假定无人机的初速度取最小速度120 km/h，由于与时刻的时间间隔为10 s，则-与-的距离为= 333.3 m。又根据-(,,)位于直线上，则可求出-的坐标-(,,)。同理可计算无人机在其他相邻时刻的飞行路径，从而确定从时刻至时刻整个过程的飞行路径，示意图如图4所示。值得注意的是，若无人机在约束条件下不能形成已知的虚假点航迹，则需要再增加无人机的数量以满足约束条件。上述求解方法也可得到无人机和的飞行路径。

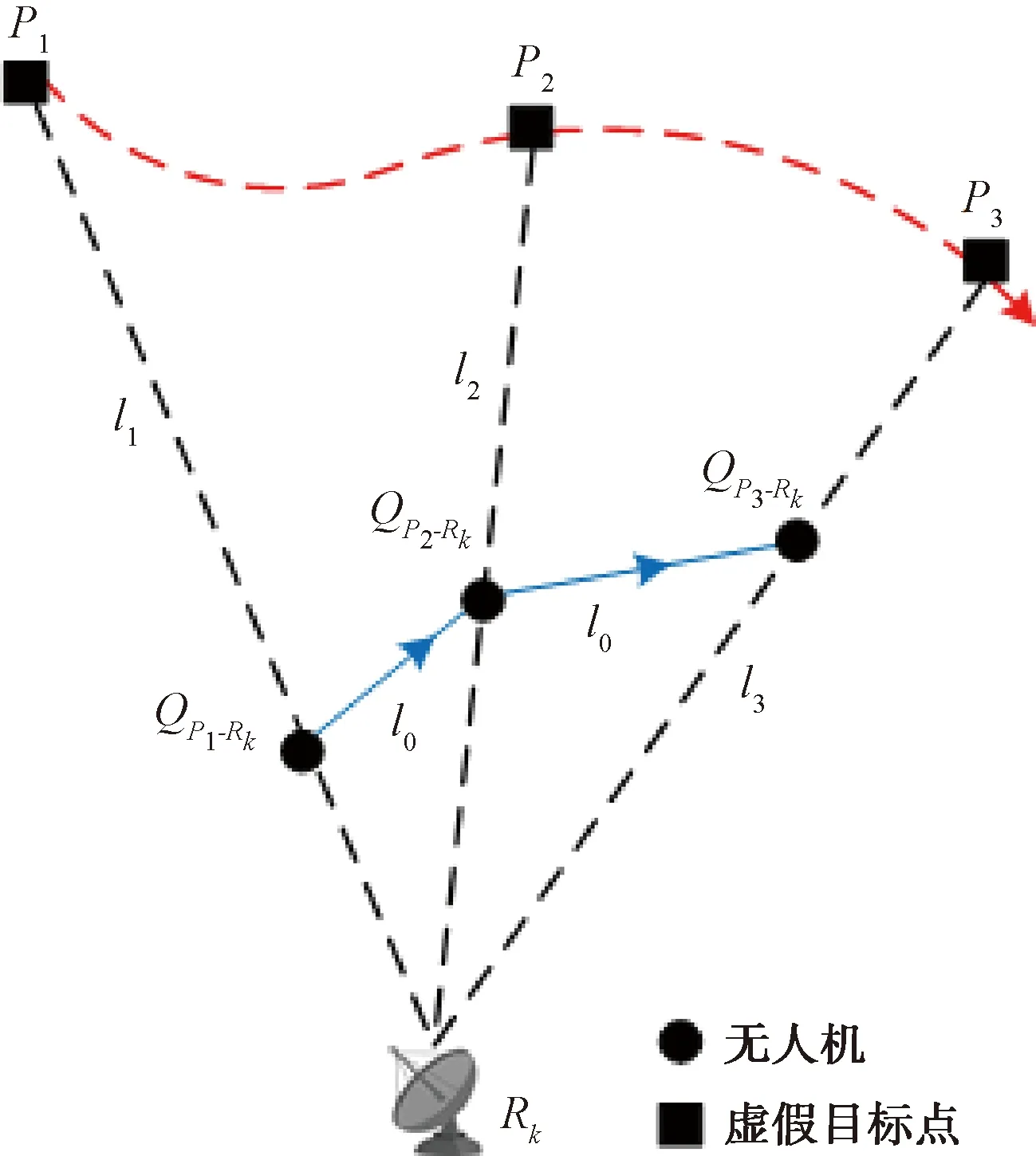
图3 无人机飞行航迹求解示意图

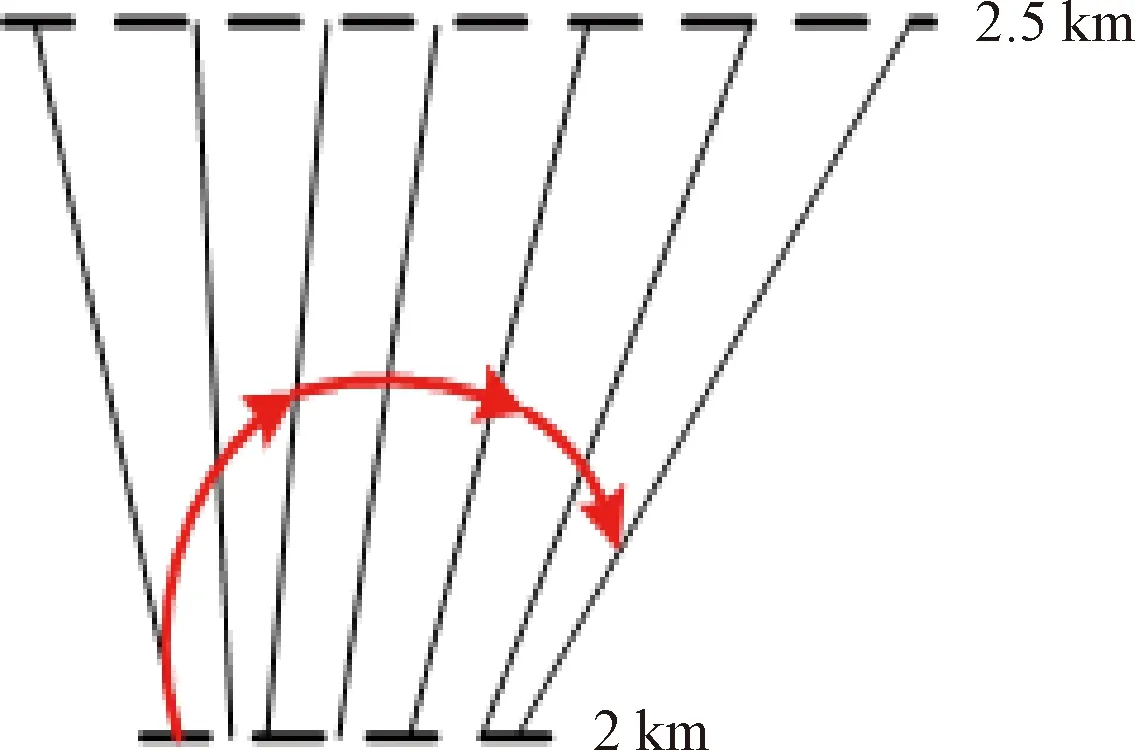
图4 无人机飞行路径示意图

4 仿真分析与评价

4.1 仿真模拟

假设某组网雷达系统5部雷达的空间位置坐标分别为：(80，0，0)，(30，60，0)，(55，110，0)，(105，110，0)，(130，60，0)，单位均为km。组网雷达的有效监测范围如图5所示，利用首点迭代法产生1条虚假航迹如图6所示，其中假目标初始位置坐标为(60 600 m，69 982 m，7 995 m)。

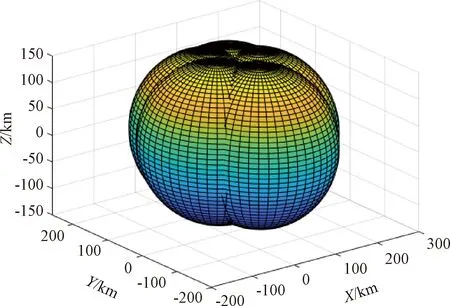
图5 组网雷达有效扫描区域

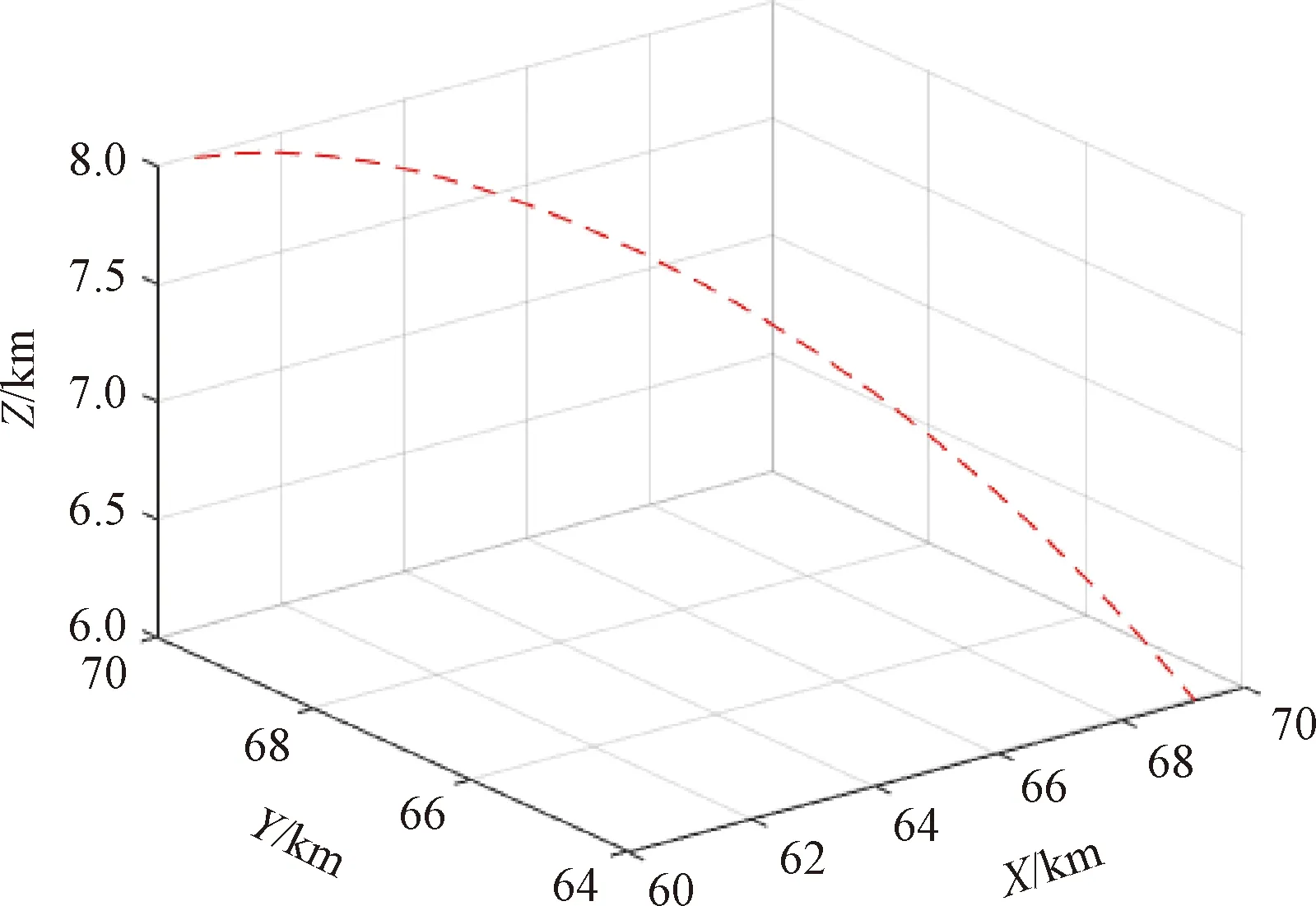
图6 假目标欺骗航迹示意图

利用3架无人机、、分别对、、这3部雷达进行干扰，协同产生了图6中的假目标航迹，3架无人机的飞行路径如图7所示。

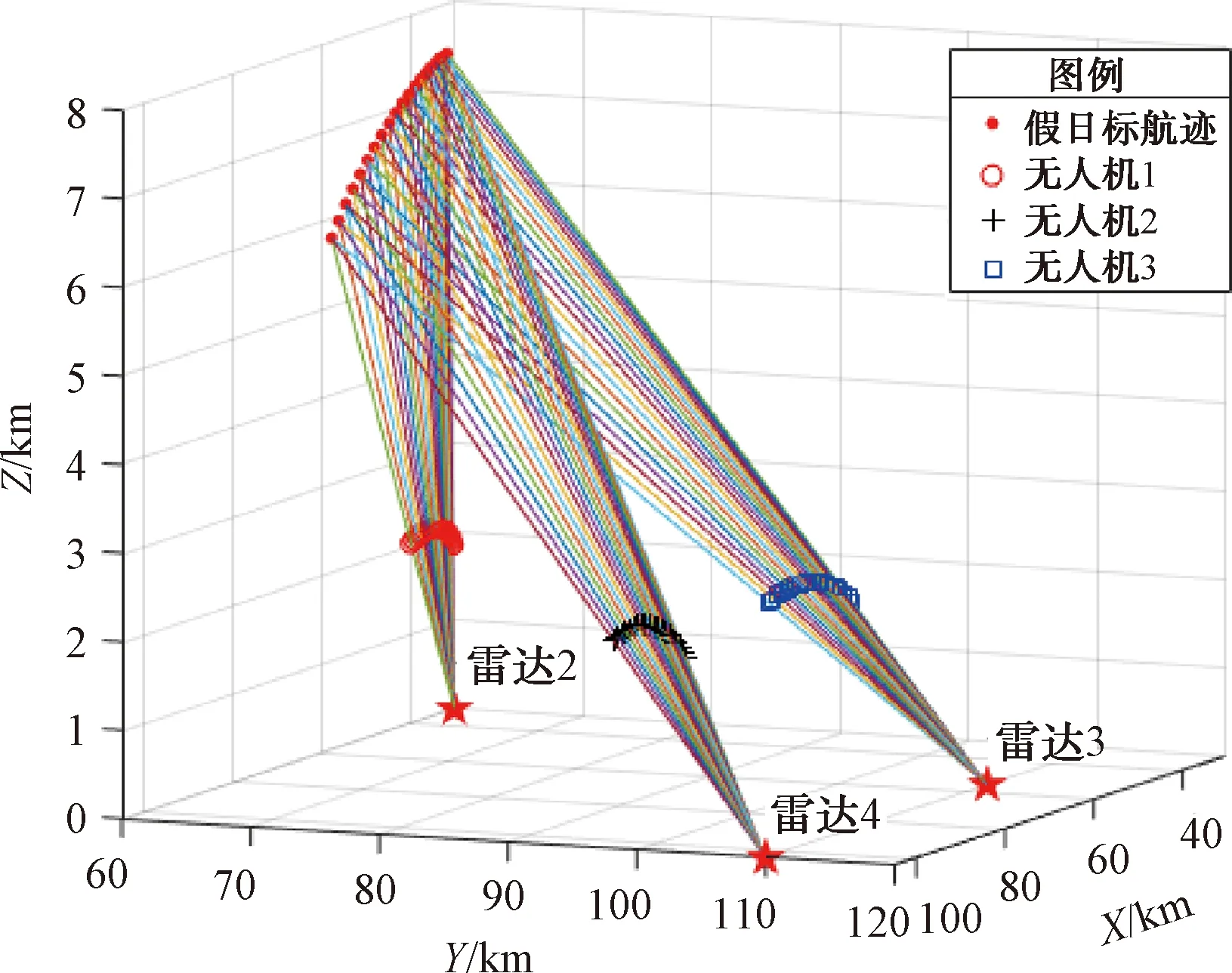
图7 无人机A1、A2、A3协同干扰雷达R2、R3、R4的飞行路径示意图

4.2 模型分析与评价

(1) 模型的鲁棒性分析

本文针对无人机转弯半径约束，给予每个参数95%的置信区间，对第3节建立的干扰模型进行鲁棒性分析，图8给出了无人机转弯半径约束取±5%时的模型求解结果的波动情况，由此可知本文建立的最优控制模型具有较好的鲁棒性。

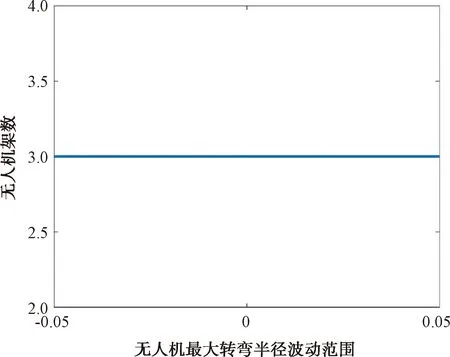
图8 模型求解结果的波动情况

(2) 模型的求解精度评价

无人机协同产生的虚假航迹与预设的虚假航迹是否完全一致能反映模型求解精度的高低。本文通过随机抽样的方法求解无人机和相应雷达连线的交点坐标及其与虚假目标点的距离，从而对模型的计算精度进行评价。在重复抽样500次的情况下，得到其距离误差的情况如图9所示。从抽样结果可以看出：相对于航迹坐标的数量级来说，使用本文方法规划出的各无人机协同干扰方案所产生的虚假目标坐标位置具有较高的精度，模型具有良好的应用价值。

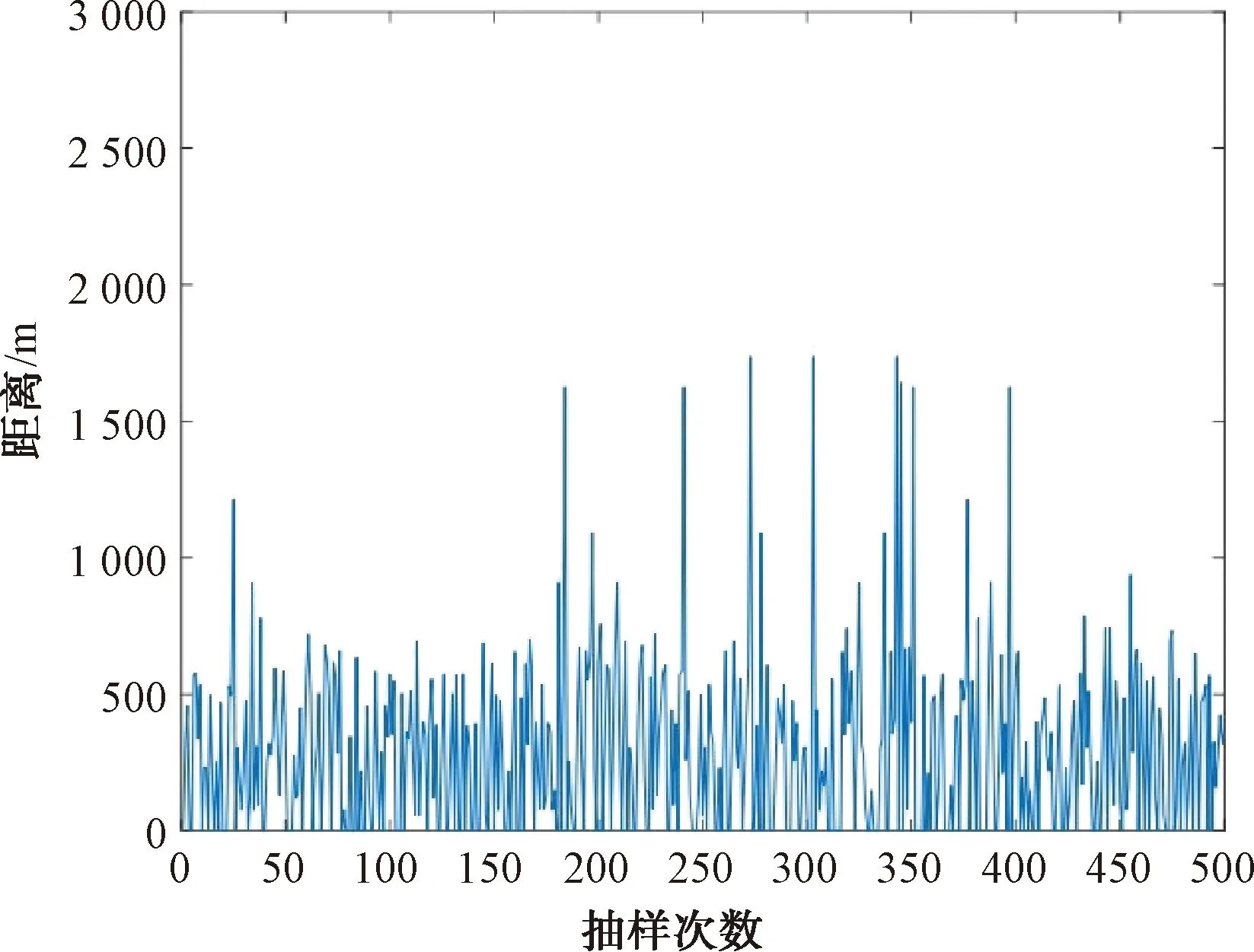
图9 虚假轨迹误差检验随机抽样分析结果

5 结束语

多无人机协同干扰是对组网雷达进行航迹欺骗的一种有效方式，本文建立了多无人机协同干扰组网雷达的最优控制模型，在给定假目标航迹数据条件下，结合相应的约束条件对模型进行了求解。仿真实验表明，本文提出的多无人机协同欺骗最优控制模型具有较好的鲁棒性和较高的求解精度，对于利用无人机对组网雷达进行协同干扰具有一定的参考价值。