持续负温环境下入模温度对水泥水化热的影响及预测模型
龙朝飞,张戎令,郭海贞,段运,肖鹏震,段亚伟
(1. 兰州交通大学土木工程学院,甘肃 兰州,730070;2. 兰州交通大学道桥工程灾害防治技术国家地方联合工程实验室,甘肃 兰州,730070;3. 甘肃畅陇公路养护技术研究院有限公司,甘肃 兰州,730070)
水泥水化是一个放热过程,期间放出的热量会影响混凝土的凝结和硬化[1]。由于我国三北地区以及青藏高原等地区均存在着大量多年冻土,冻土区钻孔灌注桩等深埋混凝土一经浇筑将立即处于负温环境中[2]。水泥的水化速率与环境温度有关[3-6],而低温条件下的水化改变了水泥基材料的流变和凝固特性[7];当环境低于-5 ℃时,由于新拌混凝土中92%的水会结冰,水与水泥基本不发生水化反应,严重影响了水泥的水化进程[8]。因此,研究负温环境下水泥的水化特性与放热规律具有重要意义。
入模温度是影响混凝土绝热温升和温升速率的一个重要因素,而混凝土的绝热温升和温升速率反映早龄期混凝土的水化速率和水化程度[9]。有研究表明,提高混凝土初始入模温度将加速胶凝材料的水化,并缩短水化反应持续时间[10]。因此,钻孔灌注桩浇筑时,若入模温度过高,则水化反应生成的大量热量将对冻土产生较大的热扰动,这可能会破坏冻土的稳定冻结状态,使得其冻结强度降低甚至融化,最终导致桩的承载力大幅下降[11-12]。因此,有必要在试验基础上对多年冻土区钻孔灌注桩水泥水化热进行定量分析,且应考虑入模温度这一重要变量。
目前,国内外学者已经针对水泥水化放热特性进行了一系列研究,并建立了一系列水化放热的预测模型。MEINHARD 等[13]建立了改进的普通硅酸盐水泥的热释放速率模型,并将其推广到混合水泥中,发现模型预测结果与直流试验数据吻合良好。李瑶[14]研究了低温环境中复合胶凝材料的水化规律,建立了基于Krstulovic-Dabic 方程的硅酸盐水泥-硅灰复合胶凝材料的水化动力学模型。该模型分段模拟整个水化历程,进一步揭示了复合胶凝材料在低温下的水化动力学反应机理。王起才等[15]建立了持续低温环境下水泥水化放热计算模型,较好地预测了不同低温环境下水泥水化放热量随龄期变化的规律。DAI等[16]研究了养护温度和水灰比耦合效应对水泥水化热的影响并提出了预测0 ℃以上和负温养护下的水泥浆体的水化热计算公式,发现水泥浆的累计水化热随养护温度的升高而增加;在负温养护条件下,水泥浆的累计水化热随水灰比增大而降低。
上述学者虽然研究了不同低负温环境下水泥的水化放热规律,并建立了一系列水化热预测模型,然而,有关入模温度、负温耦合效应对水泥水化热影响的研究较少。因此,本文作者重点研究持续负温环境下入模温度对水泥水化放热的影响规律,并建立相应的水化热预测模型,以期为我国三北地区以及青藏高原等冻土区水泥水化热的预测提供理论依据。
1 试验
1.1 试验原材料
本试验采用甘肃省永登县祁连山水泥公司生产的P.O42.5 级普通硅酸盐水泥,水泥检测指标如表1所示。试验用水为兰州市自来水,试验用水检测指标如表2所示,试验水灰比为0.38。

表1 P.O42.5硅酸盐水泥技术指标Table 1 Technical indexes of P.O42.5 Portland cement

表2 试验用水检测指标Table 2 Test water detection indexes
1.2 试验方案
冻土区按照年平均地温可分为极稳定型冻土(温度θ<-5 ℃)、稳定型冻土(-5.0 ℃≤θ<-3.0 ℃)、亚稳定型冻土(-3.0 ℃≤θ<-1.5 ℃)、过渡型冻土(-1.5 ℃≤θ<-0.5 ℃)及不稳定型冻土(-0.5 ℃≤θ≤0.5 ℃)等[17]。考虑到大多数多年冻土温度分布属于稳定型冻土,故本试验选取-5 ℃作为持续负温环境温度,并以标准养护下的试件作为对照,模拟冻土环境对水泥水化造成的影响。持续负温环境采用大气模拟箱进行模拟,大气模拟箱温度恒定调控为(-5±1)℃,该环境下的相对湿度为70%。标准养护在温度为(20±2) ℃,相对湿度为95%的标准养护室内进行。
由于GB 50164—2011[18]规定冬季施工应控制混凝土的入模温度不低于5 ℃,因此结合冻土地区持续低负温的施工环境,试验选取5,10,15 和20 ℃这4 种入模温度工况。测定水泥水化热的方法主要是直接法和溶解热法。由于直接法无法消除温升对水化反应速率的影响,且试验耗时较长,试验过程中所受干扰较大,一般只能测得前7 d的水化热。而溶解热法可以测得直接法未能测得的瞬时发热量和长龄期的水化热,便于测定水泥的水化热量尤其是长龄期水泥水化热量。因此,本文依据GB/T 12959—2008[19]中的溶解热法进行不同环境条件下水泥水化热的测定。该测试方法原理如下:依据盖斯定律,反应的热效应只与体系的初态和终态有关,而与反应途径无关,在热量计周围温度一定的条件下,用未水化的水泥与一定龄期的水化水泥分别在一定浓度的标准酸溶液中溶解,测得溶解热之差,作为该水泥在该龄期内所放出的水化热。采用溶解热法分别测试标准养护和负温环境下不同入模温度工况对应的龄期为3,7以及14~63 d(递增幅度为7 d)的水泥净浆的累计水化热,其中3,7,14,21 和28 d 时的试验数据用于建立预测模型,35,49 和63 d 对应的试验数据用于验证预测模型的精度。设计试验分组如表3所示,其中SC为标准养护下的试验组,NE为-5 ℃环境下的试验组。

表3 不同入模温度下试件分组设计Table 3 Experimental grouping design under different molding temperature conditions
1.3 试验步骤
图1所示为整个试验的流程。首先,用孔径为0.9 mm 的方孔筛筛取水泥,并将水泥充分混合均匀。然后,依据试验水灰比称取500 g水泥和190 g水,将水泥和水分别装入塑料袋和塑料水壶中,之后一并放入恒温养护箱内预温养护24 h。依据试验设置的4种入模温度工况,调节养护箱温度使得各工况下温度变化幅度不超过±1 ℃。在进行水化热试验时,将预温完成后的水泥和水从恒温养护箱中取出,快速地倒入水泥净浆搅拌机中进行搅拌。搅拌时,通过温控系统将搅拌温度分别控制在5,10,15 和20 ℃,与入模温度保持一致。搅拌完毕后及时留置试验试样,制备出的水泥净浆试样分别放入标准养护和负温环境中进行养护。待试样到达指定龄期时将试样取出,放入无水乙醇中,以终止其水化作用。在进行水化热测试之前,将样品从酒精中取出,在烤箱中干燥2 h。最后,将样品放入一个密封的玻璃瓶中,并储存在干燥器中,采用溶解热法测定水泥的水化热。

图1 水泥水化热测定试验流程Fig.1 Testing process of cement hydration heat
2 试验结果与分析
2.1 不同环境条件下入模温度对水泥水化进程的影响
图2所示为标准养护和持续负温环境下不同入模温度工况对应的水泥累计水化热和水化放热速率。图3所示为标准养护和持续负温环境下不同入模温度工况对应的水泥水化程度。

图2 不同环境条件下入模温度对水泥水化热的影响Fig.2 Effect of molding temperature on hydration heat of cement under different environmental conditions

图3 不同环境条件下入模温度对水泥水化程度的影响Fig.3 Effect of molding temperature on cement hydration degree under different environmental conditions
水化程度α是指试验中任意时刻累计水化热占理论总水化热的比例,其表达式为

式中:Qt为水泥的累计水化热,J/g;Qmax为根据水泥矿物组成计算得到的理论最大水化热,J/g。
由于普通硅酸盐水泥完全水化时的放热量为425~460 J/g[20],试验中取水泥水化完全时的放热量为454 J/g。
由图2和图3可见:随着入模温度升高,等龄期时,标准养护环境和持续负温环境下水泥的累计水 化 热Qt呈 现 以 下 趋 势:Qt,SC20>Qt,SC15>Qt,SC10>Qt,SC5,Qt,NE20>Qt,NE15>Qt,NE10>Qt,NE5,Qt,SC20>Qt,NE20,Qt,SC15>Qt,NE15,Qt,SC10>Qt,NE10,Qt,SC5>Qt,NE5。水 化放热速率v和水化程度α的变化趋势与Qt的变化趋势一致。由上述现象可以得出以下结论:
1)初始入模温度越高,2种环境下水泥的水化放热速率就越快,累计水化热和水化程度也越高。随着龄期逐渐增大,水泥水化放热速率逐步降低,水化放热变缓。这是因为,当水胶比和养护温度一定时,入模温度成为影响水泥水化反应的主要因素。不同的入模温度为水泥水化反应提供了不同的初始反应温度,初始反应温度升高提高了水分子与水泥颗粒有效碰撞的概率,加快了水泥水化反应的速率。在水化初期,水分供给充足,水化产物较少,结晶成核与晶体生长起主导作用,保证了水泥水化反应的有效进行;随着水化时间延长,水泥颗粒周围逐渐形成一层水化产物层,离子迁移变得困难,水化反应转变为相边界反应或扩散控制过程[21]。随着水分不断消耗,水化反应后期供水量不足,因此水化速率迅速减小,累计水化热增长曲线也趋于平缓。
2)当入模温度相同时,标准养护环境下水泥的水化放热速率、累计水化热、水化程度均比负温环境下的大。这是因为,在负温环境下,随着养护时间延长,水泥净浆会由初始入模温度的高能态向养护温度的低能态转变,其温度最终同环境温度保持一致。因此,在水化初期,初始入模温度保证了水泥水化反应的有效进行,但在负温环境下,水泥的水化速率比标准养护环境下的低。因此,负温环境下水泥的累计水化热和水化放热速率均比标准养护环境下的低。伴随着水化反应的持续进行,虽然环境温度为负温,但由于水化反应会生成大量水化热,故水泥浆内部将处于变温状态,使得水化反应持续进行[22]。当水化反应进行至后期,水泥浆温度已基本同环境温度保持一致,水泥水化放热速率急剧降低,放出的水化热量也大大降低。负温使得水泥浆中较大孔隙中的水结冰,不再继续水化,因而最终导致负温环境下水泥的累计水化热和水化程度低于标准养护环境下的累计水化热和水化程度。
由图2(a)和图2(b)对比可见:当入模温度为5 ℃,龄期分别为3,14和28 d时,负温与标准养护环境下的累计水化热比值分别为0.35,0.60 和0.67。当入模温度上升为10 ℃时,负温与标准养护环境下累计水化热的比值变为0.38,0.64 和0.67。当入模温度上升至15 ℃时,负温与标准养护环境下累计水化热的比值分别为0.47,0.65 和0.70。当入模温度上升至20 ℃时,负温与标准养护环境下累计水化热的比值分别为0.48,0.65 和0.75。在负温环境下,20 ℃入模温度工况在28 d内的累计水化热比5 ℃入模温度工况下的高,这表明随着入模温度升高,负温环境下水泥水化放热更加充分。这是因为入模温度升高有效地提高了负温环境中水泥的水化反应速率,在一定程度上抵消了负温环境对水泥水化放热的不利影响。对比各龄期下不同环境中水泥的水化放热速率可知:在水化早期,标准养护环境中水泥水化放热速率明显比负温环境下的大,但当水化进行到后期,2种环境下水泥水化放热速率迅速下降,但此时负温环境下水泥水化放热速率已与标准养护下的水化放热速率十分接近。由此可见当水化进行至后期时,负温抑制水泥水化的不利影响将会减弱。
2.2 不同环境下水化放热预测模型
由于水泥水化热是依赖于龄期的,因此,朱伯芳等[23]提出采用指数函数模型来计算水泥的水化热:

式中:t为龄期,d;k为经验参数。
随后,朱伯芳[24]发现复合指数函数模型用于表征水泥水化热的效果更好:

式中:λ和c为经验参数。
蔡正咏[25]采用双曲线函数模型来预测水泥水化热:

式中:m和n为经验参数。
董继红等[26]基于化学反应动力学原理,发现对数函数模型对水泥恒温水化放热有较好的拟合效果:

式中:a和b为经验参数。
邓晓等[27]发现幂指函数模型对恒定-3 ℃温度下的水泥水化规律有较好的拟合效果;

式中:γ和β为经验参数。
为了找出最适用于持续-5 ℃环境下的水泥水化热的预测模型,通过式(2)~(6)分别对标准养护和负温环境下入模温度为5 ℃和20 ℃的水化热数据进行拟合,各模型的模拟值与实测值结果如图4所示。由图4可见:由于指数函数模型前期的累计水化热增长率过快,因此,2种环境下水泥的水化热相对误差较大,但是其余4类模型均可较好地拟合28 d内标准养护和负温环境下水泥的水化热,其中双曲线函数模型的拟合精度最高。

图4 不同函数模型水化热曲线拟合结果Fig.4 Fitting results of hydration heat from function models
为了进一步评价各模型预测的可靠性,试验测定35~63 d 的水化热,各模型预测结果如图5 所示。其中,35,49 和63 d 龄期下不同模型所得水化热预测值和实测值相对误差见表4。由图5 和表4可见:标准养护环境下,63 d时双曲线函数模型可以较好地拟合水化热,其相对误差在2%以内;其余函数模型拟合结果较差,且相对误差随着龄期延长越来越大。当预测标准养护(入模温度为5 ℃)工况下63 d 龄期水泥的水化热时,式(2),(3)和(6)的预测误差分别为37.12%,15.55% 和29.89%;当预测标准养护(入模温度为20 ℃)工况下63 d 龄期水泥的水化热时,式(5)的预测相对误差为14.15%。这表明,只有双曲线函数模型可以较好地预测标准养护下不同入模温度工况对应3~63 d 龄期内水泥累计水化热。在持续负温环境下,双曲线函数模型和对数函数模型拟合精度均较高,相对误差分别在3%和5%以内,其余3类模型拟合精度较差。结合图4可以得出:无论是标准养护环境还是持续负温环境,双曲线函数模型均可以较好地预测3~63 d龄期内水泥累计水化热,而对数函数模型仅可用来预测负温环境下3~63 d龄期内水泥的累计水化热。

表4 各函数模型35,49和63 d内预测误差Table 4 Prediction error of each function model within 35,49 and 63 days

图5 不同函数模型预测35~63 d内水泥水化热Fig.5 Heat of hydration in 35-63 d predicted by different functional models
为了验证各函数模型在龄期63 d 以后的预测精度,将各拟合曲线中的龄期延长至为1 000 d,观察各模型是否符合水泥水化末期水化热的变化规律,拟合曲线延伸结果如图6 所示。由图6 可见:在龄期趋于无穷大时,幂指数函数模型和对数函数模型所得水化热增长率趋于无穷,明显不符合水泥水化规律。而指数函数模型、复合指数函数模型以及双曲线函数模型所得水化热增长率趋近于零,符合水泥水化的基本规律。由于指数函数模型无法较好地预测龄期3~63 d 内水泥累计水化热,而复合指数函数模型无法较好地预测龄期28~63 d内水泥累计水化热,因此,采用双曲线函数模型预测不同环境条件下各龄期水泥的累计水化热。

图6 不同函数模型预测3~1 000 d内水泥水化热Fig.6 Heat of hydration in 3-1 000 d predicted by different functional models
本文基于双曲线函数模型建立负温环境下入模温度对水泥水化热影响的预测模型。双曲线函数模型拟合经验参数如表5所示。由表5可知:在标准养护环境下,5,10,15 和20 ℃入模温度对应的经验参数mS和nS近似呈线性变化,如图7 所示。因此,可以推断出标准养护环境下水化热模型经验参数mS和nS与入模温度有关,从而建立标准养护环境下入模温度水化热预测模型:

图7 标准养护环境下经验参数拟合结果Fig.7 Fitting results of empirical parameters under standard curing environment

表5 双曲线函数模型经验参数拟合结果Table 5 Fitting results of empirical parameters of hyperbolic function model
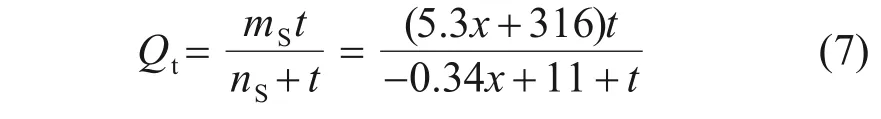
式中:x为入模温度,℃。
由表5 可知:当入模温度为10,15 和20 ℃时,标准养护环境下的经验参数mS和nS与负温环境下的mF和nF近似呈线性关系,因此推测负温环境下水化热模型的经验参数mF和nF也与入模温度呈线性关系。由图8和式(7)可以得到负温环境下入模温度水化热预测模型:

图8 标准养护和负温环境下经验参数拟合结果Fig.8 Fitting results of empirical parameters under standard curing and negative temperature environment

2.3 预测模型验证及误差分析
为了验证式(8)的精度,现将龄期为35,49 和63 d水化热实测值与模型的预测值进行对比,结果见表6。由表6 可知:仅当入模温度为5 ℃,龄期为35 d 时,负温环境下的水化热预测模型的相对误差为3.72%;其余工况下,预测模型的相对误差绝对值均在3%以内,精度较高。这说明,在持续负温环境下,双曲线函数模型中的经验参数m和n也与入模温度呈线性相关。因此,模型可用于预测持续负温环境下不同入模温度工况对应的水化热。由于建立的持续负温环境下入模温度水化热模型参数与标准养护条件相关,因此可通过标准养护条件下测定的水化热较好地预测持续负温环境下不同入模温度工况对应的水化热。由于标准养护工况下的试验条件更容易满足,因此,该模型可为我国冻土区水化热预测提供参考。

表6 水化热预测模型误差分析Table 6 Error analysis of hydration heat forcasting model
3 结论
1)负温环境延缓了水泥水化进程,提高入模温度,可使标准养护和负温环境下水泥水化放热速率增大,负温环境下水泥水化更加充分。但是随着龄期增大,负温环境下水泥水化放热速率逐渐接近于标准养护环境下的水泥水化放热速率,因此当水化过程持续至后期时,负温抑制水泥水化的不利影响将会减弱。
2) 分别采用幂指数、双曲线、对数、指数、复合指数函数模型对测定的水化热进行了拟合。通过对比分析不同龄期下各模型对水泥水化热的拟合结果,发现双曲线函数模型拟合效果最好且模型拟合参数m和n与入模温度呈线性相关。
3)建立了持续负温环境下入模温度-水化热的双曲线函数预测模型,发现该模型可以较好地预测负温环境下不同入模温度工况对应的水泥水化热随龄期变化的规律。此外,本文所提入模温度-水化热预测模型可通过标准养护环境下测定的水化热预测得到持续负温环境下各入模温度工况对应的水化热,可为我国高寒冻土区水泥水化热的预测提一定的参考。

