中低频声波强化对流换热试验研究

杨延锋，姜根山，李颢

(1. 华北电力大学能源动力与机械工程学院，北京，102206；2. 华北电力大学数理学院，北京，102206)

近年来，声波技术在电站锅炉中得到广泛应用，如声波除灰[1-2]、声波强化燃烧[3]等技术。这些技术均涉及声波作用下燃煤颗粒的传热传质特性，其作为理论基础对研究声学应用技术有重要意义。但目前有关声学技术的设备研发较多，基础理论研究较少，人们对于声场与热质传输过程的基本关系尚未形成明确的结论，因而声学技术的应用缺乏足够的理论指导。

声波诱导振荡流周期性地往复冲刷物体，不仅有助于及时清除物体表面积灰，而且有助于强化对流换热。振荡流能显著地增强流体介质间的扰动和互相掺混，从而达到强化传热、传质的目的[4-7]。目前，对振荡流动强化热、质传输过程机理的分析主要集中于旋涡脱落理论和边界层理论。有研究表明[8]，一定程度的振荡流动可以破坏固体边界上形成的边界层和加快旋涡脱落速率，从而降低对流传热和质量传输的阻力。振荡流强化传热传质的能力与振动幅值、振动频率、流体介质物性及物体结构参数等有关。量纲—参数分析表明，振动流动强化热、质传输过程的能力始终与雷诺数Re呈正比。一些学者认为振动流强化传热的能力与斯特劳哈尔数St呈正比[9-10]，另一些学者却得到了相反的结论[11-13]。对比分析发现，这与他们的实验工况有关：在高频区间，振动流强化传热的能力与斯特劳哈尔数St呈正比，其传热机理可利用旋涡脱落理论和边界层理论进行解释；在低频区间，St越小，传热越强，但对该区域传热机理的分析还很少。这也表明低频和高频振动流的传热机理是不同的。杨延锋等[14]通过实验研究了宽频率(500～1 500 Hz)范围内声波作用下直径d=5 mm的热铜球的对流换热问题，发现在500～700 Hz频段，对流换热系数与频率呈反比；在700～1 500 Hz 频段，对流换热系数与频率呈正比。杨延锋等[14]利用声流理论对低频段声波的强化传热机理进行了分析，但该研究缺乏足够的实验数据。

基于以上研究现状，本文作者以不同直径(d=10，15 和20 mm)加热铜球为研究对象，研究在中低频(200～500 Hz)声波作用下加热铜球的对流传热问题，以期为揭示低频声波的强化传热机理提供参考。

1 实验系统简介

图1 所示为声波强化换热的实验系统示意图。实验系统由声波发生系统、测温系统、声信号采集系统和实验圆管4个部分组成。研究对象为直径为10，15 和20 mm 的铜球，其导热系数均为386 W/(m-1·K-1)。声波发生系统工作原理如下：由计算机控制端经声谱仪软件(MC3642)选择特定频率的正弦信号，经功率放大器(FdB-Model TA1100)调节至特定声压级后由扬声器(8 Ω，500 W)发声。测温系统通过将K-Type热电偶感温探针一端插入开有小孔(直径约1.5 mm)的铜球内部，另一端连接到温度记录仪(YA504R)上实时记录铜球的温度变化，并将温度数据存储至U 盘。铜球被放置在距离扬声器喇叭沿面垂直高度20 cm处。温度记录仪的灵敏度为(±0.1) °C，每隔1 s 记录1 次温度，共记录60 s。铜球均加热到(140±2)°C，等温度降到(125±1)°C 时加入给定参数声波，并记录温度—时间数据。铜球初始温度为120°C，对60 s内的温降数据进行处理；待铜球温度降到环境温度时，进行下一组实验，依此重复实验，直至获取各工况的温度数据。声信号采集系统通过与铜球处于同一平面的强声声级计(MPA 471S)实时记录铜球附近的声信号，并经数据采集器传输给计算机进行实时监测和存储。

图1 实验系统示意图Fig.1 Schematic diagram of experimental system

亚克力圆管内径为115 mm，圆管有效高度为740 mm。此外，圆管顶端布置高度为275 mm的吸声棉，极大地减少管内强驻波引起的声场不均匀性。同时，圆管上端开有一直径为40 mm的出口，使热空气流出。实验过程中环境温度保持(18.5±0.5)°C。铜球的物性参数见文献[14]。

2 实验结果与讨论

2.1 实验数据误差分析

准确测量不同频率声波作用下热铜球的温度是进行数据处理和保证实验结果可靠性的重要依据。热铜球温度的误差通常与多个因素相关。实验过程中可能引起温度误差的因素主要包括：1)数据处理误差。数据处理时，均采用四舍五入的方法保留到小数点后2 位，这会产生一定的误差。2)铜球位置测量误差。每次更换铜球时，首先通过直尺标定，然后经肉眼衡量后确定铜球的中心位置，难免会带来测量误差。

实验过程中，为了尽量减小上述误差，对每个实验工况均进行2～3次重复实验。图2所示为不同直径铜球在自然散热条件下的温降曲线对比。

图2 不同直径铜球在自然散热条件下的温降曲线对比Fig.2 Comparison of temperature drop curves of copper spheres with different diameters under natural heat dissipation

由图2可知：在2次重复实验中，不同直径铜球测得的温度数据重复性较好，且2次重复实验所得温度的相对误差小于0.4%，可见实验结果是相对可靠的。

2.2 管内声场分布特性

根据声波导管理论，为使管内形成纯粹的平面声波，实验选取的声频率应远远小于圆管的截止频率。圆管截止频率fc的计算式[15]如下：

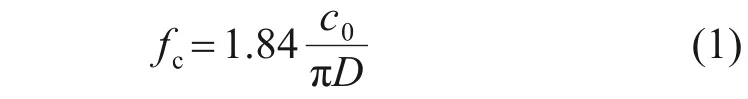
式中：c0为环境温度下的声速，为331 m/s；D为圆管内径；计算可得fc=1 687 Hz。据此，实验过程中选取中低频范围(200～500 Hz)的声频率。

为分析不同频率下圆管内的声场分布，设功率放大器的功率为80 W，不同声频率下沿圆管高度方向上的声压级分布见图3。

图3 圆管高度方向上的声压级分布Fig.3 Sound pressure level distribution in direction of circular pipe height

由图3可知：对于不同声频率，圆管内都存在平面驻波声场，这说明吸声棉并没有完全消除驻波，而是减弱了驻波的不均匀性。这是因为管内驻波效应的不均匀性取决于波长与吸声棉厚度的比，即吸声棉的吸声效果随着厚度增加而增强。由图3还可知：对于声频率为200 Hz的声波，其波长远大于吸声棉厚度，因此管内驻波声场不均匀性较大，其声压级最大差值为8 dB。随着声频率增大，声波波长与吸声棉厚度的差值减小，即驻波声场的不均匀性减弱。由此可见，在圆管有限空间内进行传热实验可以有效避免外界噪声的干扰，保证了实验声场的纯净性。

以扬声器活塞中心为原点，过中心的轴线为z轴，则扬声器沿z轴的辐射声场[15]为

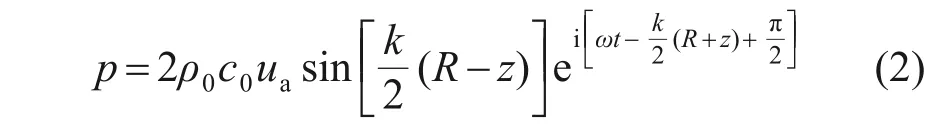
式中：p为声压；ρ为空气密度；ua为空气质点振动速度幅值；z为扬声器声源的传播距离；ω为声波的角频率；t为声波传播时间；i 为虚数单位；k为波数，k=ω/c0；R2=a2+z2，a为扬声器活塞半径，a=57.5 mm。

式(2)描述了扬声器向外辐射的远、近声场特性。正弦因子sin[k(R-z)/2]决定了声压幅值随离活塞中心的距离而变化的规律。当z很小时，即在声源附近，在k(R-z)/2=nπ(n=1，2，…)的位置上声压幅值为0 Pa，在k(R-z)/2=(n+1)π/2 (n=0，1，2，…)的位置上声压幅值为极大值。即使距离z变化幅度很小，其与k/2因子相乘后仍可能使正弦函数的辐角变化幅度较大。因此，在靠近声源附近的声场，其出现声压极大值和极小值的位置距离较近。随着距离z增加，出现声压极大值和极小值的位置相隔越来越远，如图4所示。

由图4可知，为避免声源附近不均匀声场的干扰，铜球的位置应该满足如下条件：

式中：λ为声波波长；zg为划分扬声器活塞声源近场和远场的变量。实验中选取的频率范围为200～500 Hz。对应实验中铜球的位置应满足z＞5 mm。实验中选取的距离z=20 cm，满足要求。

2.3 铜球所处位置声信号特征

为正确测定铜球附近的动态声场信号，选择合适的声级计探头是非常重要的。通过调节功率放大器使声压级逐渐增大到140 dB 左右时停留约20 s，再逐渐降低功率放大器的功率。图5 所示为强声探头和一般探头同时监测到的声压级情况。

图5 强声声级计和一般声级计测得的声压级Fig.5 Sound pressure levels measured by strong sound level meter and normal sound level meter

由图5可知：相比于一般声级计，强声声级计可以监测到更高的声压级。这是因为强声声级计可以捕捉到流体介质对强声波的非线性响应特性，如非线性引起的波形畸变等。因此，本文作者采用强声声级计进行测量。

对于给定声压级Lp=135 dB，不同声频率下强声声级计监测到的铜球附近空气介质动态响应曲线见图6。图6 中，信号幅值反映了给定声波对空气介质做功的能力。

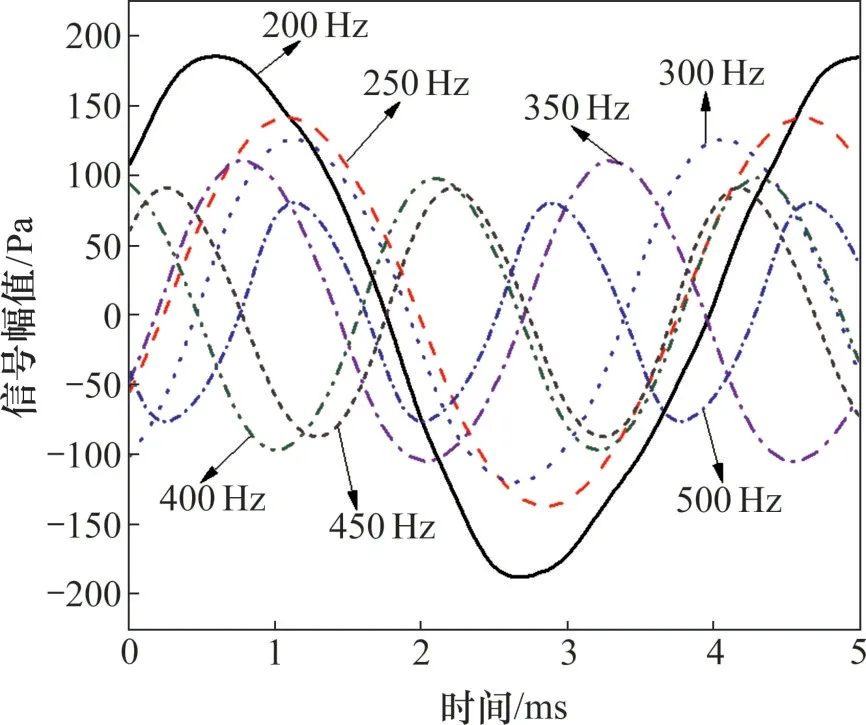
图6 不同声频率下铜球附近空气介质的动态响应曲线Fig.6 Dynamic response curves of air medium near copper sphere at different sound frequencies

由图6可知：对于不同声频率，强声声级计监测到的动态信号的幅值和周期均存在差异。声频率越低，信号幅值越大，且其波形会发生一定畸变(如声频率为200 Hz时对应的信号)。这表明低频强声波会引起空气介质的强烈扰动，非线性现象显著。在实验中，低频强声波在圆管上端出口处可以明显感受到强烈的脉动气流流动。这是因为要达到相同声压级，频率较低的声波经功率放大器调节得到的功率要大于频率高的声波的功率。这说明在相同时间内频率低的声波对空气做的功要大于频率高的声波对空气做的功。实验中感受到的强脉动气流是低频强声波在管内形成的非线性声流，也称为“声风”[16]。

为进一步说明流体介质对强声波的非线性响应行为，分析声频率f=500 Hz 时不同声压级下强声声级计监测到的声信号波形，如图7所示。

图7 不同声压级下监测到的动态声信号波形Fig.7 Dynamic acoustic signal waveform detected under different sound pressure levels

由图7可知，声压级越大，强声声级计监测到的动态声信号波形幅值越大。这表明高强声容易引起流体介质的强烈扰动。此外，高强声容易突发波形畸变等非线性现象，如Lp=140 dB对应的动态信号波形。但声压级Lp=140 dB时出现的波形畸变并不是十分明显，这是因为声级计距离声源位置较近。强声波诱导的非线性效应会随着传播距离而累积[17]。

2.4 低频声波作用下铜球的温降特性

根据文献[14]可知，声波作用下铜球温度变化满足如下控制方程：

式中：ρcop和cp,cop分别为铜球的密度和定压比热容；T(τ)为铜球在τ时刻的温度；τ为温度变化所经历的时间；V为铜球体积；A为铜球表面积；Tf为环境温度；T0为铜球的初始温度；h为对流传热系数。

式(4)可转换为

式中：M为中间变量。

式(5)为线性方程，根据实验测得不同条件下铜球的时间-温度数据，将其代入式(5)中，绘制M-τ曲线，并对其进行线性拟合，可直接得到对应的对流换热系数h。

对于给定声压级Lp=133 dB，不同直径铜球在低频声波作用下的温降曲线及其M-τ曲线数据拟合结果见图8。

由图8可知：在低频区(＜250 Hz)，频率越低，铜球温降越快，其对应的对流换热系数越大。由文献[16]可知，低频高强度声波可形成显著气流现象，气流强度随着频率的降低而增强[18]。图7所示实验结果也佐证了这一点。对比图8(a)～8(c)可知：在相同时间内，铜球直径越大，散热越慢，由吸热公式Q=cp,copmΔT(其中，m为铜球的质量，ΔT为温差)可知，加热到相同温度时，大铜球需要的热量就越多。因此，在相同参数的声波作用下，大铜球温度下降到相同温度则需要更长时间。

图8 不同直径铜球温降曲线及M-τ曲线拟合结果Fig.8 Temperature drop curves of copper spheres with different diameters and fitting results of M-τ curve

2.5 不同直径铜球对流换热系数对比分析

对于给定声压级Lp=133 dB，不同直径铜球在声频率范围为200～500 Hz 的声波作用下对流换热系数h的变化见图9。

由图9 可知：在中低频(200～500 Hz)范围内，不同直径铜球的对流换热系数h随声频率增加都呈现出先减小后增大的变化趋势。此外，由图9 可知，存在一特定频率fp，使铜球的对流换热系数h达到最小，直径分别为10，15 和20 mm 的铜球，其对流换热系数最小值对应的特定频率分别为350，300 和250 Hz，可见这一特定频率fp随着铜球直径增大而减小。当声波频率小于特定频率fp时，声频率越小，铜球的对流换热系数h越大。例如，当声频率为200 Hz时，直径分别为10，15 和20 mm 的铜球对应的对流换热系数分别为44.46，26.85 和22.27 W/(m2·K)。当声波频率大于特定频率fp时，铜球的对流换热系数h随着声频率增大而增大。

图9 铜球对流换热系数随声频率的变化Fig.9 Variation of convective heat transfer coefficient of copper sphere with sound frequency

与铜球的自然对流换热系数相比，在本文研究的声频率范围内，直径为10 mm 的铜球的对流换热过程均都得到不同程度的强化。然而，对于直径分别为15 mm和20 mm的铜球，在特定频率fp处出现了传热恶化的现象，其对流换热系数要小于铜球的自然对流换热系数。这表明特定频率fp的声波对直径为15 mm 和20 mm 铜球的对流换热过程起到了阻碍作用。根据文献[14]可知，当声波与物体发生非线性相互作用时，将在物体周围形成2种不同特性的流场，即自由振荡流和稳定声流。这2 种流场的流场特性随着声源频率的变化而变化，从而影响了铜球的对流换热过程。声频率影响自由振荡流在物体壁面上的涡脱落行为以及稳定声流的强度。已有研究[19]表明，声波诱导振荡流掠过物体时，壁面发生边界层分离，形成旋涡脱落，旋涡脱落速率随着声源频率增大而增大。同时，旋涡脱落速度还与物体结构特性有关。稳定声流的流动强度可通过流雷诺数Res描述，Res=U02/(2πfυ)，其中U0为声波引起的流体介质质点速度振幅，υ为流体的运动黏度。由此可见，声流的流动强度与声强呈正比，而与声频率呈反比，与物体的结构参数无关。

综上可知，直径分别为15 mm 和20 mm 的铜球在特定频率fp处出现传热恶化。这是因为在特定频率fp处，声波诱导自由振荡流在铜球壁面上没有发生旋涡脱落行为，在声波作用周期内，始终存在附着在铜球壁面上的涡结构，形成了较厚的热黏性边界层，这极大地增加了传热热阻，阻碍了铜球与周围环境之间的换热过程。与此同时，该特定频率fp处的声流作用也很小。当声频率小于特定频率fp时，随着频率进一步降低，自由振荡流对传热的影响已基本不变，而声流的作用越来越强。在低频强声作用下，铜球周围可以形成强烈的伴随旋涡特性的声流，这类旋涡声流可以破坏铜球壁面上的热黏性边界层。因此，在低频区，声流的作用又再次强化了铜球的对流换热过程。在声波频率大于fp的区域，声流的作用变得很弱，这时自由振荡流在铜球壁面上形成的旋涡随着声频率增大而逐渐分离，加速了铜球的对流换热过程。

图10所示为相对努塞尔数Nur(Nur=h/h0)随量纲一参数ka的变化规律。图10中，ka=πd/λ。

由图10可知，相对努塞尔数Nur随着ka增加都呈先减小后增大的趋势。声波强化传热的能力随着铜球直径增大而减小，传热效果越差(即Nur越小)，对应的ka越大。对d=10 mm 的铜球，当ka=0.019 时，声波强化对流传热的效果相比自然对流时提升约77%。对于d=15 mm(ka=0.028)和d=20 mm(ka=0.038)的铜球，铜球的传热效果分别提升60%和50%。可以预见，ka越小，声波强化对流传热的效果越好。

图10 相对努塞尔数Nur随ka的变化规律Fig.10 Variation of relative Nusselt number Nur with ka

3 结论

1）在低频强声波作用下，实验圆管内形成了声流(声风)的强气流现象。

2）对于给定声压级，加热铜球的对流换热系数h随着声频率f逐渐增加而呈先减小后增大的变化趋势。当f=200 Hz 时，相对于自然对流换热，铜球的传热效果分别提升了77%(d=10 mm)，60%(d=15 mm)和50%(d=20 mm)。

3）在中低频声波作用下，存在某一特定声频率fp使加热铜球的对流换热系数h出现最小值，且在声频率fp的声波作用下，直径为15 mm和20 mm的热铜球出现了传热恶化的现象。这表明声波既能强化对流换热过程，也能阻碍热传递。出现传热恶化的特定频率fp与铜球直径呈反比。