温度分层流体中潜航器激发内波试验

吴 炎，李宇航，陈 科*，蓝林欣

(1.上海交通大学 海洋工程国家重点试验室，上海 200240)(2.上海交通大学 三亚崖州湾深海科技研究院， 三亚 572000)

近年来，关于潜艇探测和隐身问题已经受到越来越多的关注，在潜艇的降噪技术取得巨大突破后，潜艇的噪声级已降至与海洋背景噪声级接近[1]，传统的声学探潜技术已经受到制约，而热红外探潜技术因其独特优势而成为当今热门研究课题，是目前非声隐身的重点研究内容之一[2-4].研究表明，当水下物体在温度、密度垂向层化的海洋中航行时，艇体及其尾迹的扰动会使海水微团偏离其平衡位置进而形成内波[4-5].当流场存在温度梯度时，海水微团携带的热量会随着其偏离的同时到达其上(下)温层，二者存在温差发生热量的传递，使稳定的温度场，出现温度异常的信号.目前对这些温度扰动信号进行非声探测成为一种潜在的军事手段[6].因此，研究海洋热分层的形成过程及水下航行体移动过程对温度分层产生的影响十分必要.

在阳光照射下，海水会在空间上表现出温度的不均匀特性，在海洋内部存在稳定的温度层结[7].海水温度的不均匀性与盐度和压强的不均匀性共同导致了海水密度在垂直方向上出现分层的特征.海水的上下分层之间存在温度差，而且上层与下层之间存在温度连续变化的过渡层，这种过渡层称为温度跃层.由于海洋温度分层会受到不同外力因素的干扰，因此虽然原则上对于温度盐度分层产生的扰动可以通过如拉曼和布里渊散射等手段进行探测，但实际效果并不佳，这也导致以往直接观测潜艇内波尾迹的相关研究相对稀少，目前多采用数值模拟的方法在分层流体中捕获潜航器激发的内波尾迹[8-13].在海洋中进行内波试验和捕捉内波结构极具挑战性，因此在试验室尺度下探究内波的相关性质具有十分重要的实践意义.

目前国内外学者对水下航行体在航行过程中产生的影响进行了理论上的分析和数值计算,但在试验层面上依旧有所欠缺，且研究方向多停留于盐度分层流体环境，对海洋中温度分层现象及航行其中的水下航行体产生水温扰动特性等相关研究相对匮乏.文中针对这一短板而开展研究，一方面验证了大型水槽的温度分层技术；另一方面给出航行体在温度分层环境中的内波特性的初步结果.

在参考文献[6]的温度分层理论后，建立了一套试验室尺度下模拟海洋温度分层现象的温度分层试验系统，同时增加水池长度，优化温度.考虑到与自然界温度分层的相似关系及文中研究对象为内波，在参考盐度分层达到稳定所需参数条件后[4]，决定采用Froude数作为相似准则.关于内界面Froude数Fr，其定义为：

(1)

式中：U为航行体运动速度，cm/s；D为航行体特征尺度，一般取航行体的最大直径，cm；N为浮力频率，一般取主跃层的最大浮力频率，rad/s.

其中浮力频率计算公式为：

(2)

式中：ρ为垂向密度分布，kg/m3；g为重力加速度，m/s2；z轴设定方向向下.

考虑到与自然界分层的相似性及盐度分层常采用浮力频率N来描述分层流体的主要特征[4]，为统一标准方便比较，试验也采用浮力频率来描述温度分层流体.

对于真实海洋的情况，考虑潜航器的直径取为约10 m，航速为10～20 kn，即约5～10 m/s；根据南海实测，主跃层浮力频率大约为0.01 rad/s；盐度分层达到稳定时浮力频率大约为2 rad/s[5];试验温度跃层达到稳定时浮力频率约为0.4 rad/s.则对于直径10 m、航速10 m/s的潜航器在自然界主跃层与直径0.07 m、航速1.5 m/s的模型在盐度、温度分层中航行所对应的浮力频率N与Fr对比关系如表1.

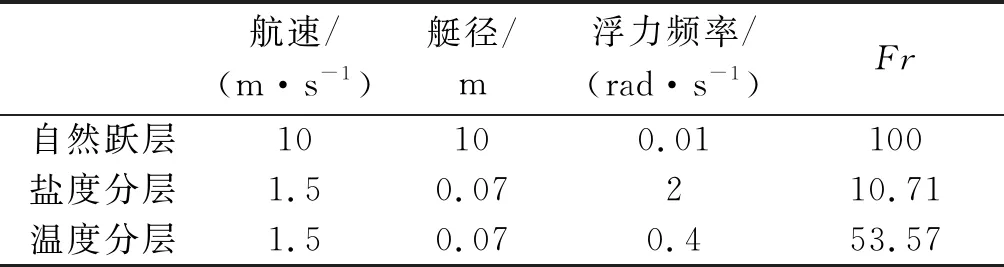
表1 不同分层之间的参数对照

由表1可知，虽然温度分层的模拟方式与自然界主跃层仍旧存在差距，但相较于盐度分层其Fr上限已有巨大提升，同时对于潜航器激发内波产生扰动特征的问题研究，此时的Fr上限已经满足试验需求.试验采用的上述试验系统，探究潜航器在温跃层内激发内波所产生的温度扰动特性，有利于进一步增强对内波特征相关课题的研究.不同于难以监测的密度波动，温度扰动具有更明显的变化特征，也更具备实用价值.

1 试验方法

1.1 试验设备

试验在解放军陆军工程学院的温度分层水池进行，水池尺寸为长12 m、宽1.2 m、高1 m，水池主体为钢架结构且底面与侧面采用高强度透明玻璃，采用循环拖曳法牵引潜航体模型航行，在水池两测中心线对应位置各放置一个拖曳支架，拖曳支架的导轨可通过水平丝杠和垂直丝杠调节，实现调节试验模型的横向位置及潜深的试验设置.在其中一个支架上安装有一个电机，电机受伺服控制器控制，可对伺服控制器设置航行距离和拖曳速度等参数.试验拖曳速度可调范围为10～150 cm/s，实际最大运动距离约为1 000 cm.试验采用国内先进温度采集系统，测量精度可达到0.02 ℃，分辨率优于0.005 ℃，采集频率可达50 Hz，同时该采集仪具有64个采集通道，可实现同时段流场同步温度监测，观察到流场温度动态变化，使采集结果的准确性更高.

1.2 相似准则

对于试验的相似准则主要采用Fr相似与几何相似.

几何相似主要用于控制跃层位置和潜艇潜深等参数：实际海洋的跃层位置h在水下50 m至100 m处，潜艇直径D约为10 m，则潜艇直径与水深之比D/h=0.1～0.2.水池高1 m，因此考虑试验安全问题，加水至0.8 m，则将实际海洋跃层位置换算至试验中的跃层位置为0.35～0.7 m，综合考虑后选取试验跃层位于水下约h=0.35 m处，对应于实际海洋水下h=50 m处，试验模型缩尺λ约为1∶140.

1.3 试验方案

1.3.1 水下航行体布置方案

在温度分层流水槽中布置水下航行体模型.如图1，取在水槽左端的自由液面处为坐标原点o，其中自由表面设为oxy平面，以水槽的中新线纵剖面作为oxz平面，以水槽的横剖面作为oyz平面.潜航体模型的中心线与水槽的中心线重合，潜艇中心轴线距水平面的距离d为潜深.潜航体两端系于循环拖曳线，由伺服电机循环系统驱动，控制潜航体的行进距离与行进速度.潜艇中心线上方有一根平行于拖曳线的牵引钢丝，距离拖曳线高度为10 cm，两端固定于支架， 保证潜艇行进过程中其运动姿态保持稳定.

1.水下航行体；2.循环拖曳系统；3.潜航体牵引线；4.拖曳线；5.稳压电源

1.3.2 温度探头布置方案

由预试验可知，温度跃层出现位置约在距水池底部40 cm处，因此温度探头阵列沿垂向布置方案为：第一组在10、15、20、25 cm处布置4个探头，Δz1=5 cm；第二组在28、30、32、34、36、38、40、42、44、46、48、50、52、54、56 cm处布置15个探头，Δz2=2 cm；第三组在60、65、70、75、80 cm处布置5个探头，Δz3=Δz1=5 cm.分别在距离原点o沿纵向长度y=5 cm，x=500、600、700、800、900 cm处布置温度探头阵列，同时在x=600 cm，y=±40、±30、±20、±10 cm处布置温度探头阵列.某一组温度探头阵列沿垂向布置方式如图1.

1.3.3 试验工况设计

对于真实海洋的情况，考虑航行器的最高航速为20 kn，即约U=10 m/s；试验几何相似比例为1∶140， 因此潜航体拖曳模型的航速范围设定为5～120 cm/s.由于环境温度变化会对试验结果产生影响，因此对于每个工况进行重复性试验并将数据取平均值降低误差.

将拖曳系统伺服控制器与拖曳支架相连接，在拖曳系统操作界面上设置拖曳速度及航行体行进速度.每次拖曳试验完毕后需静止30～40 min，使水池内温度分层流体恢复稳定状态，方可进行下一次拖曳试验，其工况如表2.

表2 拖曳工况表

2 温度跃层模拟试验过程

2.1 海洋温度跃层模拟

试验通过控制智能热能转换装置输出介质温度及循环系统管道数量控制温差，进行加热管与冷水管温差为5 ℃的分层试验.试验开始前需注水至80 cm处并静置30 min保证水池内流场各部分理化性质均匀稳定，设置加热智能转换系统的输出温度的上限与下限，保证热能转换装置输出温度稳定.文中试验采取开启6根循环系统加热管.同时开启温度监测系统，进行温度实时监控采集

2.2 温度跃层形成过程

试验水池加热过程中其垂向的温度T变化规律如图2；其浮频率N变化曲线如图3.

图2 加热过程中水池垂向温度变化情况Fig.2 Vertical temperature change of the pool during heating

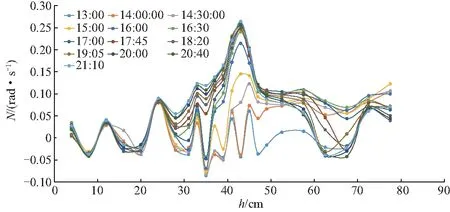
图3 加热过程中浮力频率变化曲线Fig.3 Buoyancy frequency curve during heating

在图2中可观察到距离底部0～25 cm间池水温度T波动范围为0.4～1.7 ℃，在距池底高度h为30～45 cm，温度变为16.7 ℃，温度梯度为1.113 ℃/cm，此区域就是所得到的温度跃层.在距水池底部50～80 cm的区域的流体温度已经与加热管壁相同且温度梯度趋近于零.

由式(2)可计算获得水池加热过程中其垂向浮力频率数值，绘制成图3.图2中在温度跃层稳定后水池内流体温度依旧存在波动，但从图3可知在浮频率最大处(深度z=43 cm)，浮力频率N的最大波动为6.3%<10%，可认为温度跃层依旧保持稳定.

沿水池横向取3个监测点、纵向取5个监测点，计算其浮力频率.经计算可知在浮频率最大处(z=43 cm)，3个横向剖面的浮频率N的最大波动为0.583%，5个横向剖面的浮频率N的最大波动为1.42%，关于水池横向、纵向的浮频率波动均远低于10%，因此说明此时水池内流体的温度场温度分布均匀，得到了一个沿水池横向、纵向温度均匀且稳定的流场.该流场上层厚度约为30 cm，底层厚度近似为30 cm；中间为一个温度连续变化的温度跃层流体，厚度约为15 cm，最大浮力频率在深度z=43 cm附近，Nmax=0.265 79 rad/s.

3 水下航行体在温度分层环境下产生的波动

在已完成的模拟海洋温度分层环境中对水下航行体行进不同航速、潜深的拖曳试验，探究有潜航体经过的稳定温度分层的流场温度扰动变化情况.

3.1 潜航器

拖曳模型的型线为SUBOFF，如图4.模型艇体由流线回转体形头部和尾部，以及圆柱形中间主体部分组成，附体包括位于头部的围壳及位于尾部的十字型尾翼.艇体总长度L=56 cm，中间部分圆柱形的直径D=7 cm，即长径比λ=8.艇身用玻璃钢制作，内部腔体中空，用于配重.

图4 潜航器模型Fig.4 Model of underwater vehicle

3.2 潜航器对存在稳定温度分层流体的扰动影响

3.2.1 潜深30 cm时不同航速拖曳试验

(1) 试验设置

开启6根加热管采用5 ℃温差温度分层，潜深30 cm，初始温度10.93 ℃，至14∶40跃层保持稳定，跃层位置出现在43 cm处.其加热完毕后温度T变化剖面如图5，浮力频率N分布如图6.

图5 30 cm潜深拖曳温度变化剖面图Fig.5 Profile of towed temperature change at 30 cm depth

图6 30 cm潜深拖曳浮力频率变化剖面图Fig.6 Change profile of towed floating frequency at 30 cm depth

由图5、6可知，虽然拖曳过程中流体温度发生变化，但浮力频率最大值始终出现在z=43 cm处，且最大浮力频率波动=3.80%远小于10%，可认为温度跃层始终维持在z=43 cm处，试验所得数据是客观有效的.

根据式(1)计算出试验过程中不同航速U对应的Fr，则潜深30 cm，不同拖曳速度对应Fr如表3.

表3 30 cm潜深，不同航速对应Fr

由长径比可知，临界Fr≈0.238 1λ+1.767 9=3.666 7.则在淡水温度分层流场中，相比于重力作用，其惯性力作用占主导地位，航速变化对流场的温度扰动影响较为明显.

(2) 潜深30 cm时航速U与分层流体温度关系

将距池底高度为43 cm所有温度探头采集到的温度数据减去背景温度后，得到不同航速U工况下，温度变化的时历曲线，分析温度关系曲线获得不同通道的最大相邻波峰与波谷的温度差值，对所有通道的最大相邻温度差取平均值，将该平均值记作内波最大峰-峰值并绘制航速与温度扰动变化峰-峰值(图7).

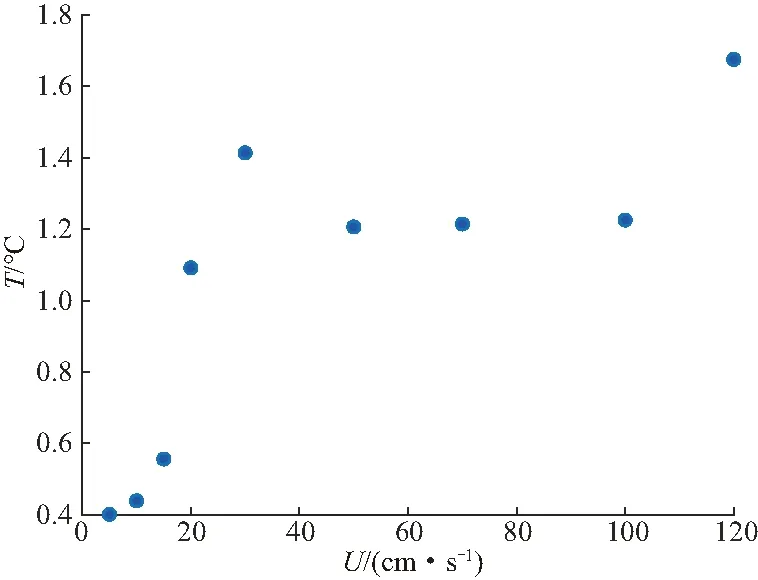
图7 潜深30 cm，不同航速与跃层温度变化峰-峰图Fig.7 Depth of 30 cm, different ship speed and thermocline temperature change crest diagram

由图7可知，对于在温度分层的流体中存在一个临界速度Uc=50 cm/s，在低航速状态下(U≤Uc)，潜航体在有温度分层的流场中对温度场的扰动效果随航速增加而显著增加，且近似于线性关系；在航速达到临界速度后(U>Uc)，温度扰动峰-峰值不再随航速增加而改变；当航速继续增加，突破速度Ud=100 cm/s后，会出现温度扰动继续随航速变化的现象.

出现上述情况是因为在低航速阶段，流场温度扰动主要来源于潜航体行进过程中产生的体积效应内波，航速增加，潜航体对其表面流体产生的扰动效果增强，产生温度波动增大；当航速达到Uc后，此时内波的主要激发源开始从体积效应内波转向尾迹效应内波；当航速突破极限速度Ud后，内波主要激发源为尾迹效应内波，此时航速再次成为温度扰动的主要因素.此现象与文献[5]采用盐度分层所发现转捩情况有共性，将于后面讨论.

(3) 潜深30 cm时温度扰动时空特征

将采集的数据信号转化为温度变化数值，绘制其温度变化灰度图，可直观的反映出当水下航行体对存在温度跃层的分层流体产生的水温扰动效果随时间的变化关系，掌握潜航体运动状态与温度变化之间的关系.其不同拖曳速度产生的温度扰动时空特性通过灰度图如图8.

图8 30 cm潜深时不同航速产生的水温扰动时空特性Fig.8 Spatio-temporal characteristics of water temperature disturbance caused by different ship speeds at 30 cm depth

潜航体在水下行进过程中会对均匀稳定的流场中的流体产生扰动，在存在温度分层的环境下，流畅内不同垂向高度的流体温度不同，潜航体行驶过后会对其产生扰动，使原本处于该位置的流体受到挤压，运动到其他温层，由于受到挤压的液体温度与其他温层的温度不同，可通过温度传感器监测到温度异常信号，进而通过温度的变换反映出潜航体的运动状态.由图8可知，当航速较低时如图(a)～(c)，其扰动多体现为横波系，随着航速的增加如图(d)～(f)，横波系逐渐消失侧波系逐渐加强，在航速达到一定程度后，主要表现为侧波系，如图(g)～(i).从图(a)～(e)可观察到，条纹的亮暗程度随航速增加而明显，而图(f)～(h)中的条纹其亮暗程度不随航速增加而改变，这与图7的航速与温度扰动变化峰-峰值关系相一致.

3.2.2 潜深20 cm时不同航速拖曳试验

(1) 试验设置

开启6根加热管采用5℃温差温度分层方式，将潜深调整为20 cm.初始温度9.8 ℃，至17∶00加热完毕跃层稳定，跃层位置出现在43 cm处，其温度变化剖面图如图9；浮力频率分布如图10.

图9 20 cm潜深拖曳温度变化剖面图Fig.9 Profile of towed temperature change at 20 cm depth

图10 20 cm潜深拖曳浮力频率变化剖面图Fig.10 Variation profile of towed buoyancy frequency at 20 cm depth

根据式(1)计算出试验过程中不同航速下对应的Fr，则潜深20 cm，不同拖曳速度对应Fr，如表4.

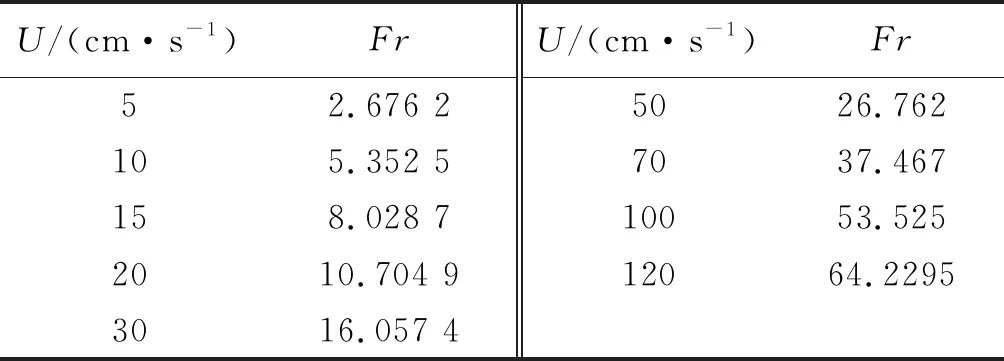
表4 20 cm潜深，不同航速对应Fr

浮力频率波动小于10%，由长径比可知，其临界Fr≈0.238 1λ+1.767 9=3.666 7.则在淡水温度分层流场中，相比于重力作用，其惯性力作用占主导地位，航速变化对流场的温度扰动影响较为明显.

(2) 潜深20 cm时航速U与分层流体温度关系

重复拖曳试验，将采集到的温度数据消除背景温度扰动后，计算其对应通道所采集的温度扰动波峰与波谷差值，对其中所有探头对应的最大值取平均值，该平均值为对应航速下的温度峰-峰值，绘制航速与温度扰动变化峰-峰值图，如图11.

图11 潜深20 cm，不同航速与跃层温度变化峰-峰图Fig.11 Depth of 20 cm, different ship speed and thermocline temperature change crest diagram

由图11可知，在潜深为20 cm时，其航速与跃层温度变化关系和30 cm潜深时的规律近似，区别在于20 cm潜深处温度梯度较小，产生的热扰动温差较小.

3.2.3 潜深10 cm时不同航速拖曳试验

(1) 试验设置

开启6根加热管采用5 ℃温差温度分层，将潜深调整为10 cm，初始温度11.33 ℃，加热至14∶30跃层保持稳定，跃层位置出现在43 cm处.其加热完毕后温度T变化剖面图如图12，浮力频率N分布如图13.

重复拖曳试验，将采集到的温度数据消除背景温度扰动后，计算其对应通道所采集的温度扰动波峰与波谷差值，取其中最大值绘制航速与温度扰动变化峰-峰值图.

图12 10 cm潜深拖曳温度变化剖面图Fig.12 Profile of towed temperature change at 10 cm depth

图13 10 cm潜深拖曳浮力频率变化剖面图Fig.13 Variation profile of towed buoyancy frequency at 10 cm depth

潜深10 cm，不同拖曳速度对应Fr，如表5.

表5 10 cm潜深，不同航速对应Fr

浮力频率波动小于10%，由长径比可知，其临界Fr≈0.238 1λ+1.767 9=3.666 7.则在淡水温度分层流场中，相比于重力作用，其惯性力作用占主导地位，航速变化对流场的温度扰动影响较为明显.

(2) 潜深10 cm时航速U与分层流体温度关系

重复拖曳试验，将采集到的温度数据消除背景温度扰动后，计算对应通道所采集的温度扰动波峰与波谷的最大差值，并对所有通道的最大温度差值取算术平均值，绘制航速与温度扰动变化峰-峰值图(图14).

图14 潜深10 cm，不同航速与跃层温度变化峰-峰图Fig.14 Depth of 10 cm, different ship speed and thermocline temperature change crest diagram

由图14可知，在潜深为10 cm时，其航速与跃层温度变化关系和30、20 cm潜深时规律近似，在U=50 cm/s附近存在临界速度Uc，区别在于10 cm潜深处温度梯度较小，产生的热扰动温差较小.

4 试验结果与理论模型对比

在潜航器激发内波理论模型方面，等效移动质量源理论较为成熟，但其主要研究对象为球体，对于轴对称回转体存在一定的不适用性，因此采用文献[14]提出的等效质量源理论模型和文献[4]提出的不同长径比拖曳体模型的体积效应激发源的参数确定方法以及尾迹效应激发源的正对称和反对称等效源的组合设置方法及其参数确定方法，将所得出的理论结果与前述试验结论进行验证.

4.1 源致内波理论

源致内波理论的基本思想是在内波控制方程组的连续方程中加入激发源.由前述试验结果可知，运动物体产生内波的激发源主要分为两大类：一类为体积效应；一类尾迹效应.若能够建立与试验模型的运动参数、几何参数等相关联的等效源模型，则可从理论角度对水下航行体生成内波特性进行研究.

由于体积效应内波的产生机制可归结为物体本身及其附带回流区产生的排水效应，由于这两类激发源均跟随物体一起运动，因此体积效应内波相对于物体的运动是定常的.试验结果表明：当航速U<临界速度Uc时，体积效应内波为主控内.文献[4]提出对于转捩前的体积效应内波可以采用正对称源作为等效质量源，而对于转捩后的尾迹效应内波的产生机制较为复杂，包括湍流涡激发的随机内波，尾迹塌陷产生的内波，以及晚尾迹扰动产生的内波等.且转捩后，尾迹效应内波波幅随拖曳速度增大而增大，这是一类大尺度湍流相干涡结构激发的尾迹内波.本文试验结果表明：当U>Uc时，体积效应内波会迅速衰减直至消失，此时尾迹效应内波会取代体积效应内波而成为主控内波.而且尾迹效应激发源并不跟随物体一起运动，其运动速度要远小于模型的拖曳速度，其密度扰动具有时空随机性.同时，尾迹效应内波即存在正对称成分也存在反对称成分.

4.2 结果对比

在参考文献[4]所采用的密跃层扰动计算方法后，对于理论解依旧采用体积等效源和尾迹等效源即奇偶组合源的思想进行模拟，其中正对称激发源和反对称激发源采用球体源模型.

同时考虑其将波数转换为空间位移的思想，利用在温跃层中激发内波的空间位移与温度变化可以相互转化换的特性，可将理论数值解中的空间位移转化为温度扰动，同试验结果进行对比.

如图15，采用等效质量源与激发源参数设置法[4,14]后得到温度变化数值解与潜深z为30、20、10 cm时拖曳试验测得温度扰动变化结果对比关系.

由图15可知，在转捩前内波垂向幅值的计算结果与试验结果吻合性较好，虽然该模型是提出者主要针对盐度分层建立的，但是盐度分层与温度分层有一定的相似性，二者都是通过改变流体密度形成分层现象，同时在水下航行体航速不高时，体积效应内波为内波的主要激发源，其产生的内波扰动相对于航行体而言是定常的，因此受扰动的流体微团同时携带盐度与温度出现在其它流层并产生盐度和温度方面的扰动，而其产生的扰动效果就可以反映内波一些特征.因此在未发生转捩时，盐度与温度的相似性使其在反映内波特性上存在一定的相似性，可以真实地反映出内波地实际情况.

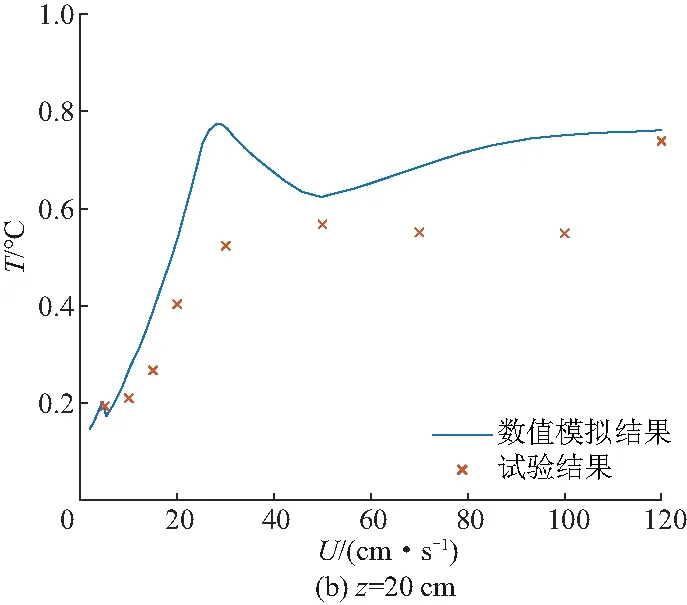
图15 内波垂向温度扰动数值解与试验测得温度波动Fig.15 Numerical solution of internal wave vertical temperature disturbance and temperature fluctuation measured experimenta

在转捩后，内波垂向幅值的计算结果与试验结果误差较大，这说明在内波地激发源转为尾迹效应内波后，温度与盐度地扰动出现了不同步地现象.这是因为所使用的模型处理方法，是利用密度沿垂向变化可以转化为深度z的函数(ρ=ρ(z))，因此可以根据密度变化进而得到流体微团沿垂向产生的扰动位移，最终得到内波高度幅值，所研究对象主要是盐度分层，流体密度较大.而试验结果则是根据直接测得的温度数据转换得到，研究对象是温度分层.温度和盐度有一定的相似性，二者都是通过影响流体的密度进而出现分层现象，但又有所不同.此外由于航速增加，尾流产生的脱落涡、湍流尾迹或混合区引发的重力塌陷会强化扰动区域的换热效率，使温度达到均匀的时间大大缩短，温差信号减弱不容易被监测到.而且温度不同于盐度，在受到扰动后，如果流体微团的温度与新到达的环境温差较大，则在一定程度上会增加换热效率，使温度快速区域一致，使温度信号难以捕捉.同时温度流场对环境的变化较为敏感，当环境温度发生变化时，对温度的测量效果会有一定的影响.

5 结论

(1) 对于在温度分层的流体中存在一个临界速度Uc，在低航速状态下(U≤Uc)，潜航体在有温度分层的流场中对温度场的扰动效果随航速增加而显著增加，且近似于线性关系；在航速达到临界速Uc后，温度扰动效果不会随着航速增加而增大；当航速继续增加，突破速度Ud后，会出现温度扰动继续随航速变化的现象.

(2) 温度所引起的密度变化弱于盐度，因此温度分层内的Fr普遍大于盐度分层，水下航行体用相同的航速行驶时，盐度分层中流体微团所受到的扰动较温度分层中的小，导致试验所得扰动结果低于密跃层计算结果.同时发现临界速度Uc的某些特性与密度分层拖曳试验的转捩点有相似之处，可以用于判断潜航体是否处于转捩，进而判断内波激发源的种类.

(3) 采用温度分层拖曳试验所得结果在体积效应内波阶段与理论结果一致性较好，而在尾迹效应内波阶段则出现了较大的偏差.分析后得出结论:计算结果是基于盐度变化产生密度差异进而得出内波高度关系，盐度分层与温度分层不同，盐度分层的流体微团密度较大，未转捩时，受到扰动后其分层稳定性更高，而转捩后温度分层中的流体则因尾流产生的剧烈扰动而强化换热效率，同时温度传递又受温差影响，进而导致计算结果与试验结果在转捩后偏差较大.同时理论模型有待于优化.