基于机动单元库的TSO-GRU-Ada机动轨迹预测

唐上钦， 魏政磊， 谢磊， 周欢， 张卓然

(1.空军工程大学 航空工程学院， 陕西 西安 710038；2.中国空气动力研究与发展中心, 四川 绵阳 621000；3.93184部队, 北京 100000)

0 引言

机动轨迹预测是自主空战的重要组成部分，对机动决策影响深远。在实际对抗过程中，拥有轨迹预测的一方会迅速占据态势优势，满足攻击指标。轨迹预测实际上是时间序列的预测问题，且具有高度的非线性和时变性。按照现有预测方式的不同，机动轨迹预测可以分为两类：模型驱动类与数据驱动类。

模型驱动的机动轨迹预测方法是基于一定的先验知识，根据目标的运动规律，建立精准的动力学或运动学模型。文献[3]通过在线识别各类机动动作建立轨迹预测模型，实时预测目标位置，但在机动变化较为频繁之际，预测精度有所下降；文献[4]利用气动参数设计机动模式集，通过蒙特卡洛采样和贝叶斯理论实现轨迹预测，相比于传统的外推理论精度更高，但要求建立一个较为完善的机动模式集，在实际情况中很难进行完善；文献[5]针对气动参数控制的飞机运动模型，设计了自适应交互多模型进行轨迹预测，但该方法要求目标在短时间内姿态变化不大；文献[6]提出了一种灰色动态滤波方法进行轨迹预测，相比于传统的卡尔曼滤波和原始灰色方法预测精度大幅度提高，但其利用最小方差估计值代替实际值，引入微分方程，无法对参数准确估值，不准确的参数都会导致误差较大；文献[7]采用交互式模型解决轨迹预测问题。基于卡尔曼滤波的机动轨迹预测方法受到飞机运动模型与算法精度两个方面的制约，同时基于交互多模型算法的预测方法通过加权多种模型来提高预测精度，但是仍然受到运动模型的限制。

基于数据驱动的机动轨迹预测方法是通过提取轨迹规律实现未来时刻的轨迹预测。从数据驱动的角度看，解决机动轨迹预测问题的思路分两种：一种是将轨迹预测问题视为函数拟合问题；另外一种是将其看作为时间序列的预测问题。前者是将机动轨迹看作静态数据进行拟合，不具有动态性；文献[9]研究了目标机动轨迹的特征，提出一种基于最小二乘曲线拟合的目标机动轨迹预测方法；文献[10]利用小波分析法提高轨迹的识别能力，采用小波分解预测方法建立了轨迹外推方案，该方案对数据处理要求较高，实际过程中所采集的数据往往会有一定的偏差。基于时间序列的轨迹预测方法包括自回归模型、隐马尔可夫模型、高斯混合模型、模糊时间序列预测、Elman神经网络、循环神经网络(RNN)。RNN预测方法包括RNN、长短期记忆(LSTM)神经网络、门控循环神经网络。文献[15]提出了一种飞机4D轨迹预测模型，将卷积神经网络(CNN)与LSTM网络结合，预测精度相比于单一模型更高，但其缺点是只能进行短期预测，且飞机轨迹变化不能过于剧烈，适用范围有限；文献[16]提出了一种深度编码和深度解码的LSTM网络用于轨迹预测，提高了预测的准确性和鲁棒性，但其仅应用于飞机航行的终端空域，终端空域的轨迹都较为平滑，在复杂轨迹情况下预测精度会大幅降低；文献[17]改进了飞行动力学模型，设置偏航角速度阈值，利用CNN卷积核共享减少了存储空间和训练时间，从局部信息聚合得到整体信息，对输入进行层次信息的提取；文献[8]利用门控循环单元(GRU)预测飞行轨迹，通过对比不同网络层数和神经元个数，选取最优GRU网络，与反向传播(BP)神经网络对比，预测误差降低。

通过上述研究可知，基于模型驱动的预测方法在线预测实时性较强，但需要对目标建立较为完善的模型，实际飞行过程中很难建立完备模型；基于数据驱动预测方法易于实现，在数据全面且充分的情况下预测精度较高，因此采用基于数据驱动的机动轨迹预测方法。本文的主要贡献为：

1)考虑到机动轨迹在三维空间中复杂性较高，通过4种轨迹特征，将轨迹分为三类，划分为21种基本机动单元，构建更加完备的机动库，使得复杂轨迹简单化，数据需求量大幅度减少；

2)采用三角形搜索优化(TSO)算法代替梯度下降算法更新门控循环神经网络内部权值和偏置，克服了局部最优问题，缩短了预测时耗，一定程度上提升了预测精度；

3)利用自适应增强技术构建强预测器，进一步提升了预测精度，通过仿真选取最优网络参数。

1 无人战斗机模型及机动单元库建立

1.1 无人战斗机3自由度模型

采用以油门、攻角和滚转角为控制量的无人战斗机(UCAV)3自由度模型，其模型示意图如图1所示。图1中，为空气阻力，为升力，为发动机推力，表示UCAV的速度，、分别表示俯仰角、偏航角，(，，)表示UCAV的空间坐标位置，′表示速度在水平面上投影。

图1 UCAV推力模型Fig.1 Thrust model of UCAV

UCAV模型的数学公式定义如下：

(1)

式中：为飞机质量；表示重力加速度。在该模型中，(,,,,,)为状态量，(，,)为控制量。

在飞行过程中，由于油料的消耗，自身质量会减轻，速度由消耗系数决定，其公式如下：

(2)

推力、阻力和升力受飞机外形、飞行状态和环境因素影响，其计算公式分别为

(3)

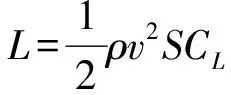
(4)

(5)

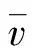
1.2 机动单元库建立

机动轨迹可以分为水平面机动动作、垂直面机动动作和空间组合机动动作。在水平面内，根据航迹偏转角，机动轨迹可以分为平飞、右转弯和左转弯。一般情况下，航迹偏转角变化率Δ为正，表示飞机正在左转；否则表示飞机正在右转。如果航迹偏转角变化率累加角度达到90°或者-90°，则累加开始到当前时刻的机动轨迹被认为是一段被分解的左转弯或者右转弯机动轨迹；如果累加角度从90°达到180°，则表示该段轨迹为左转弯；如果该段轨迹继续左转弯，则累加角度会超过180°，此时累加角度重新归零累加，且角度为负。右转弯机动轨迹的分解与左转弯一样。直飞保持当前的航迹偏转角不变，其变化率为0°。水平面内的机动轨迹单元分为3种，如图2所示的、和。

图2 机动轨迹单元示意图Fig.2 Schematic diagram of maneuver trajectory unit

在垂直面内，根据倾斜角、高度变化率，机动动作可以分为爬升与俯冲。对于高度增加的爬升机动，如半斤斗倒转机动动作可以由两个轨迹片段构成，首先是航迹倾斜角由0°变为90°，其法向加速度偏上方，轨迹形状为凹上爬升形状；其次是航迹倾斜角由90°变为0°，其法向过载偏下方，飞行轨迹为凸上爬升形状。两种形状的差异主要由飞机滚转角相差180°造成，而目标机的姿态与过载是UCAV传感器无法得知的，因此采用航迹倾斜角变化率来区分垂直面内的轨迹形状；同时，利用累积倾斜角来区分爬升与俯冲。垂直面内的机动轨迹单元分为6种模式：凹上爬升、直上飞、凸上爬升、凸下俯冲、直下飞、凹下俯冲，如图2(a)所示的～。

在空间中，可以将一个空间动作分解为水平面内机动与垂直面内机动。按照水平面内的分类，将空间机动轨迹单元分为两大类：空间左转弯机动与空间右转弯机动；再按照垂直面内的分类，将空间左转弯机动分为左转弯凹上飞、左转弯直上飞、左转弯凸上飞、左转弯凸下飞、左转弯直下飞以及左转弯凹下飞，空间右转弯类似于空间左转弯。空间左转机动轨迹单元具体分类如图2(b)所示的～。与左转弯类似，空间右转机动轨迹单元具体分为右转弯凹上飞、右转弯直上飞、右转弯凸上飞、右转弯凸下飞、右转弯直下飞以及右转弯凹下飞(除了水平右转弯)，如图2(c)所示的～。

在空间分布划分的基础上，根据上述分析将航迹倾斜角(航迹切向方向与水平面夹角)、航迹倾斜角变化率Δ、偏航角(航迹切线方向与图1中轴夹角)和偏航角变化率Δ作为机动单元的分类参数，建立机动单元库，如表1所示，相比于传统的7种或11种机动单元库更加全面，能够涵盖各种复杂的机动动作。

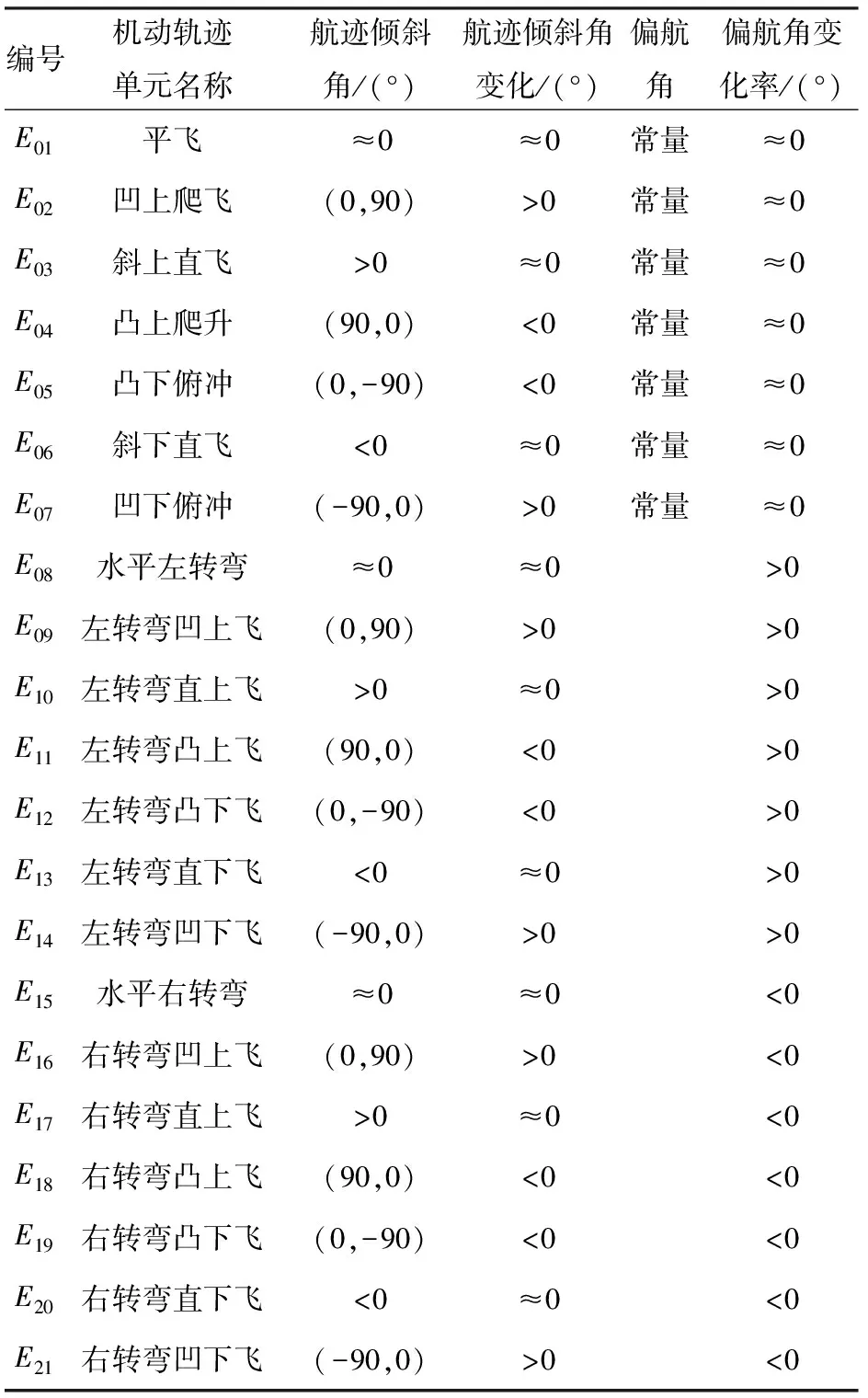
表1 机动轨迹单元特征

2 集成三角搜索优化GRU神经网络

为解决机动轨迹预测精度低、时耗高的问题，本文提出集成三角搜索优化GRU神经网络(TSO-GRU-Ada)模型。为克服GRU的梯度优化陷入局部最优的问题，利用一种三角搜索算法来优化训练GRU的权重与偏置量。同时为了增加预测精度，结合自适应增强算法改进GRU神经网络。

2.1 GRU神经网络

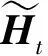
图3 门控循环神经单元结构图Fig.3 Structure diagram of gated recurrent neural unit

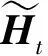
=(,+-1+)

(6)

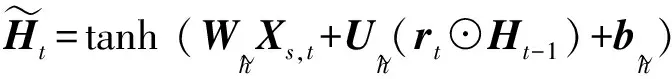
(7)

=(,+-1+)

(8)

(9)

,=(,++)

(10)

2.2 三角搜索优化算法

神经网络权重与偏置量训练学习是一个优化问题。为克服GRU可能陷入局部最优问题，采用一种基于三角形启发的进化优化算法——TSO算法。

TSO算法分为角度搜索(TVS)阶段与边搜索(TES)阶段。具体步骤如下：

1)初始化三角顶点种群。

2)TVS阶段。将顶点种群分为进化算子种群与高斯分布估计算子种群。该阶段具体的流程如下：

第1个子群采用高斯分布估计算子更新个体，计算公式为

=+,～(0,)

(11)

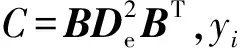
=,～(0,)

(12)

为特征向量矩阵，=diag(,,…,)为特征值对角矩阵，表示第个特征根值，表示问题的维度，表示第个单位长度的搜索方向，服从标准正态分布。

第2个子群根据当前点与其他两个点之间的夹角类型，采用不同的进化策略更新个体。3个点之间的夹角类型主要分为锐角、钝角(包括直角)和无效角，第个顶点个体的夹角计算公式为

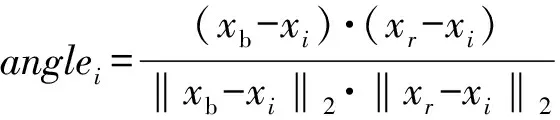
(13)

式中：表示目标向量中的最优个体；表示第(≠)个顶点个体。根据夹角类型，具体进化策略定义如下：

①如果当前的夹角是锐角，则对应的顶点采用两个差分进化算子，具体策略计算如下：

(14)

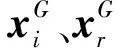
②如果当前夹角为钝角或者直角，则采用两个差分进化算子：

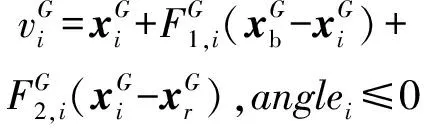
(15)

与(14)式不同的是，(15)式第2个差分进化算子发生变化，主要是加快种群优化收敛速度。

③如果当前的顶点不能构成三角形，则视当前的夹角为无效角度，这种状态采用current-to-best1变异策略。

3)TES阶段。设为贪婪参数，∈(0,05)。将种群分为较优解、中间解和较差解3类，各类所占种群比重分别为、1-2和，更新公式为

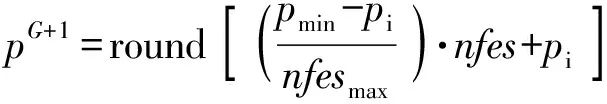
(16)

为提高种群搜索多样性，TES利用较优解和较差解之间的差分向量与中间解之和来更新种群个体，计算如下：

(17)

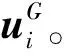
(18)

6)如果当前评价次数达到最大评价次数，则停止优化过程，并且输出最优值吗，如果未达到最大评价次数，则返回步骤2。

2.3 集成TSO-GRU网络

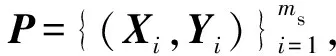
1)初始化时间序列样本的权值分布=(,,…,1,)，每个样本的权值计算如下：

为了达到WHO-FIP药学教育人才培养“八星药师”目标和我国临床药学专业培养目标，基于布鲁姆学习目标分类法，中国药科大学构建了临床药学专业本科生的实践教学体系。

(19)

2)对于迭代轮次=1,2,…,，使用具有当前分布的训练器的训练样本，训练基预测器=(,)。

3)计算基预测器在训练样本集上的预测误差率：

(20)

(21)

=max |-()|

(22)

式中：,为第个样本在第个基预测器上的相对平方误差；为第轮的样本最大误差。

4)计算基预测器的权重系数：

(23)

5)更新训练时间序列集的样本分布+1，直到迭代轮次达到最大值：

(24)

6)线性组合个基预测器，得到最终的强预测器：

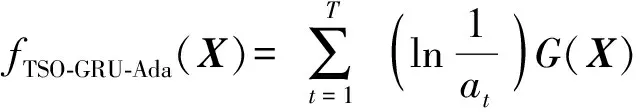
(25)

式中：()为所有()的中位数。

将TSO优化器与传统SGD、Adam优化器进行对比，损失函数收敛曲线如图4所示，可知TSO优化器收敛速度更快，优化效果更佳。

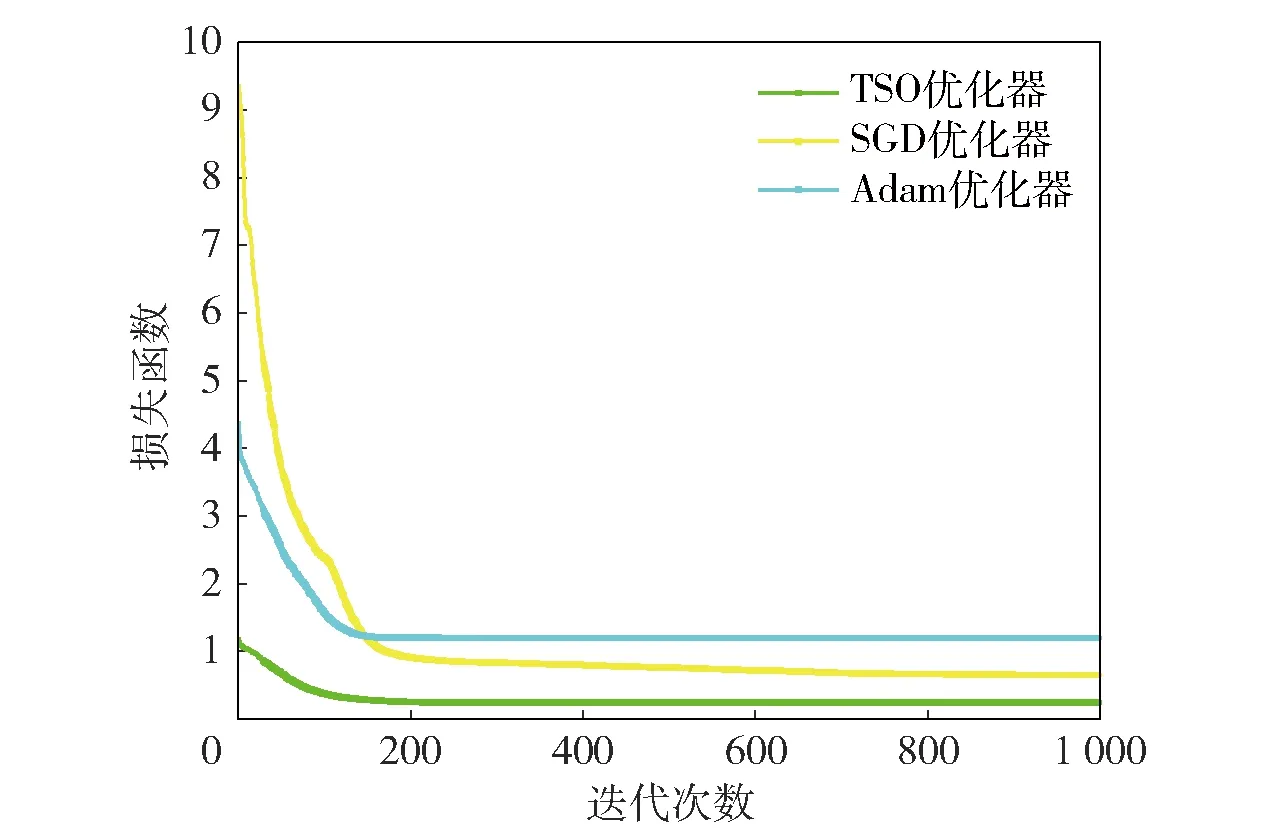
图4 损失函数收敛曲线Fig.4 Convergence curve of loss function

3 基于TSO-GRU-Ada的机动轨迹预测方法

结合自适应增强学习器(AdaBoost)与TSO-GRU，提出一种基于TSO-GRU-Ada的目标机动轨迹预测模型。该预测模型主要是以历史时刻机动轨迹坐标为输入，以未来时刻的机动轨迹坐标为输出，挖掘机动轨迹的运动规律。除此之外，每一种机动单元训练一个预测模型，选取普适结构，这样防止出现过拟合现象。基于TSO-GRU-Ada的机动轨迹预测模型如图5所示。具体步骤如下：

1)获取训练样本。利用3自由度模型机动训练飞行参数数据提取轨迹参数，构建21种机动训练样本集{(,)}(=1,2,…,21)。

2)初始化AdaBoost参数。初始化基预测器算法TSO-GRU，基预测器个数′；初始化训练样本的分布权重′。

图5 基于TSO-GRU-Ada的机动轨迹预测流程Fig.5 Flow chart of maneuver trajectory prediction based on TSO-GRU-Ada

3)训练基预测器TSO-GRU。初始化TSO种群，即初始化GRU网络参数；执行TSO的变异操作(包括TVS与TES阶段)；执行交叉算子；计算预测均方误差；执行精英选择策略。执行上述优化过程直到迭代结束，输出GRU最优网络权值与偏置量，计算训练样本的预测输出。

4)计算权重系数以及更新样本分布+1；训练基预测器直到迭代轮次结束，输出强预测器TSO-GRU-Ada。

5)通过当前时刻机动单元，选取强预测模型，利用实时目标轨迹特征参数测试强预测器。

4 轨迹预测仿真

为验证TSO-GRU-Ada预测模型解决空战机动轨迹预测问题的可行性与有效性，首先利用UCAV 3自由度模型得到大量基本单元飞行轨迹，利用机动轨迹参数获取TSO- GRU-Ada的AdaBoost基预测器个数、GRU隐藏单元个数、TSO种群规模；其次，利用UCAV轨迹构建训练集训练TSO-GRU-Ada网络，利用轨迹建立测试集检验TSO-GRU-Ada的性能；最后在空战训练测量仪(ACMI)系统中抽取一组机动轨迹进行预测。为验证本文提出方法的优越性，将TSO-GRU-Ada与Elman、LSTM、GRU、TSO-LSTM、TSO-GRU作比较，具体参数设置如表2所示。利用UCAV运动学模型获得21种机动单元样本集，其速度马赫数随机分布为0.3～0.9，在每种机动单元训练轨迹数100，测试轨迹数10，其中轨迹采样间隔为0.1 s，单次输入周期为 10 s，预测周期为2 s。实验仿真环境为Windows 10，CPU为 2.80 GHz，8 GB内存，编程软件MATLAB。每个仿真实验运行20次，每次运行轮数如表2中所示，统计20次的预测结果。

表2 机动轨迹预测方法参数设置

4.1 TSO-GRU-Ada参数仿真分析

4.1.1 不同种群规模的影响

首先从TSO的种群规模入手进行分析。不同机动单元的不同种群规模对TSO-GRU-Ada的影响结果如图6所示。从图6中可以看出，随着种群规模的增加，TSO-GRU-Ada模型的机动轨迹坐标预测值均方根误差(RMSE)减小，预测时间变化不大；相同种群规模下，每种机动轨迹单元的RMSE与预测时间变化不大。综上分析，为了考虑到预测模型训练时间，选取种群规模为25。

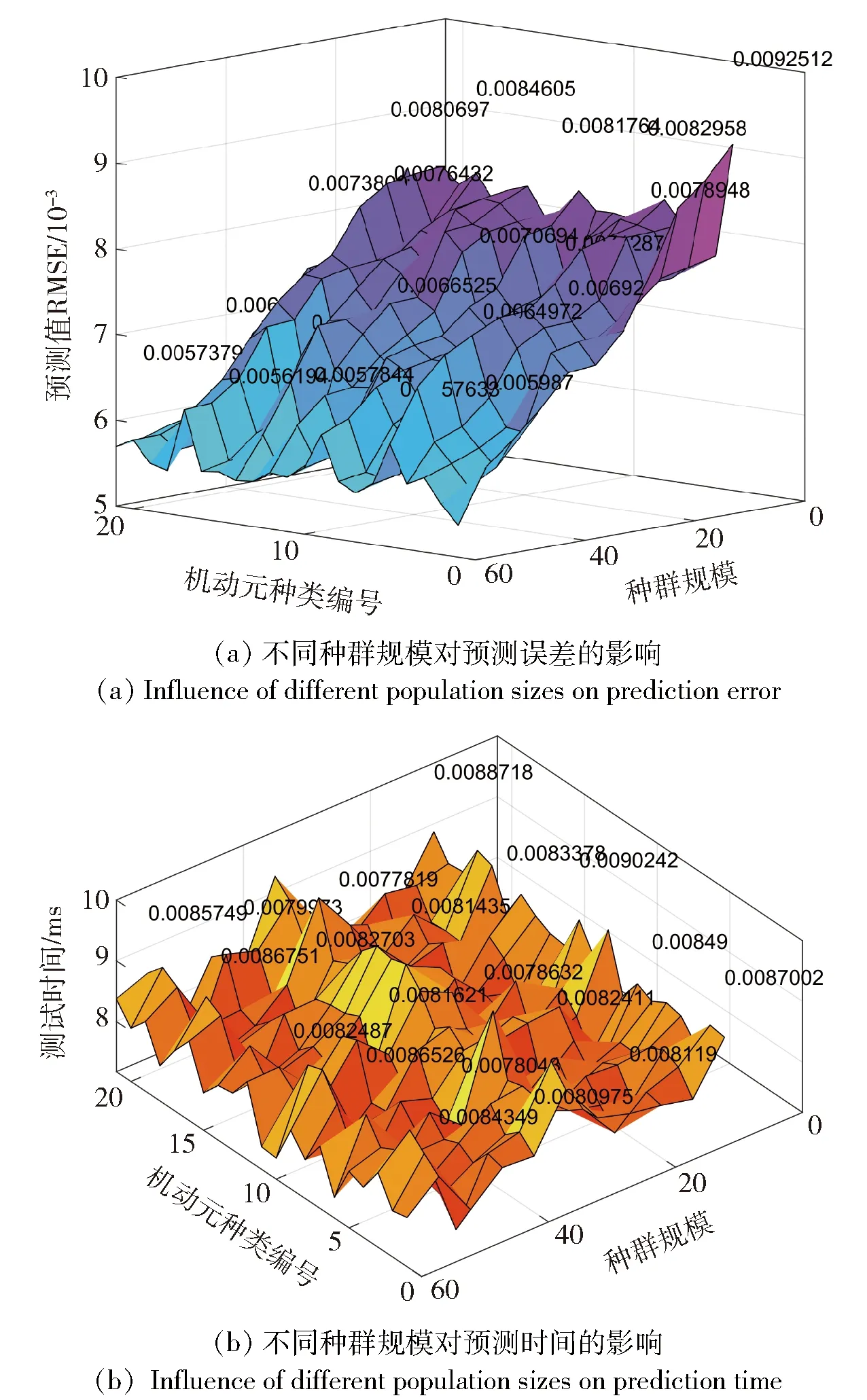
图6 不同种群规模对TSO-GRU-Ada预测性能的影响Fig.6 Effect of different population sizes on the prediction performance of TSO-GRU-Ada

4.1.2 不同基预测器个数的影响

在不同机动轨迹单元情况下，不同基预测器个数对TSO-GRU-Ada预测性能的影响结果如图7所示。从图7中可以看出，随着基预测器数目的增加，TSO-GRU-Ada模型的预测RMSE减小，预测时间增加；在相同基预测器数量下，21种机动轨迹单元的RMSE与预测时间变化不大。综上分析，本文选取基预测器个数′=8。

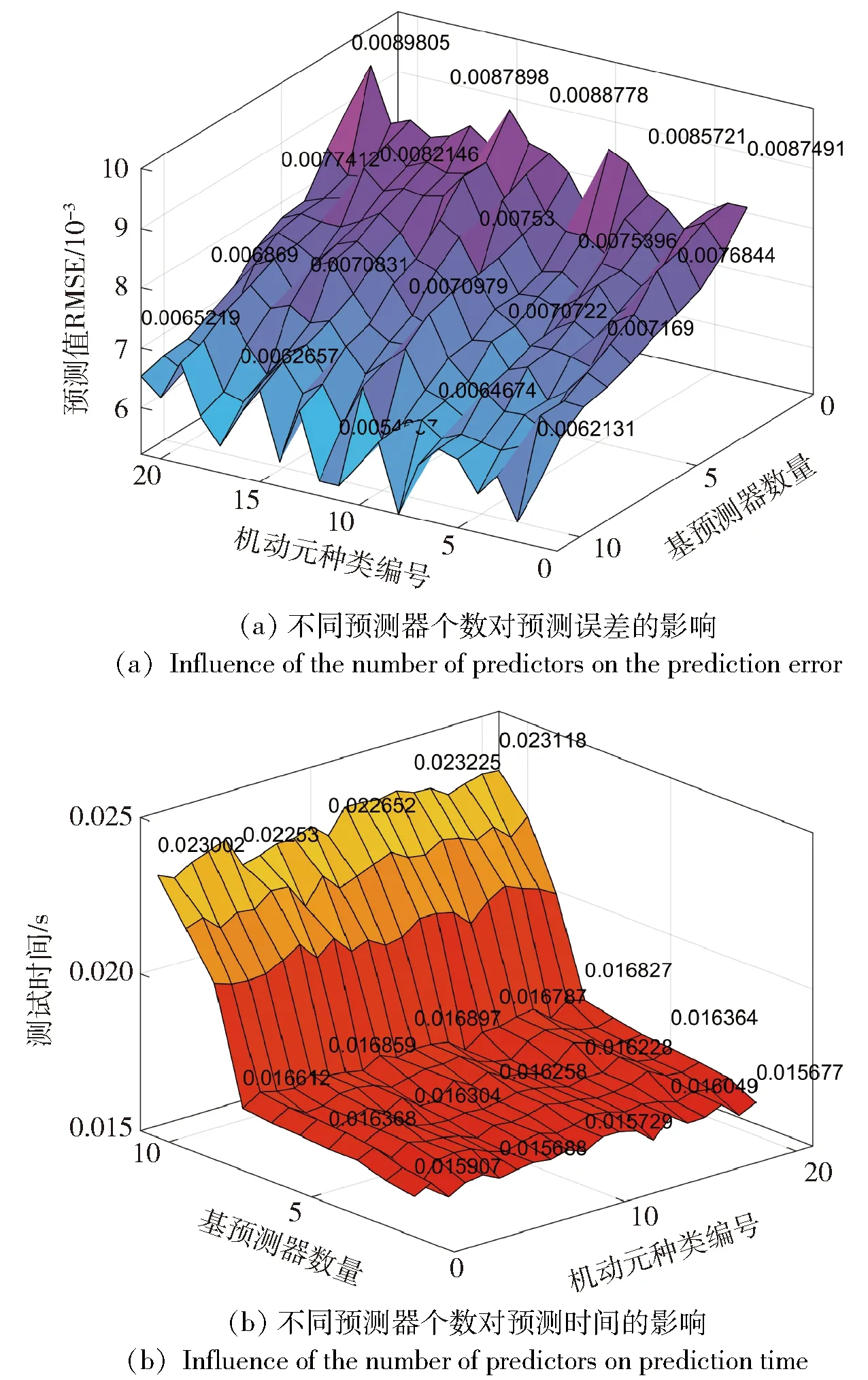
图7 不同基预测器个数对TSO-GRU-Ada预测性能的影响Fig.7 Effect of the number of base predictors on the prediction performance of TSO-GRU-Ada

4.1.3 隐层单元数的影响

在不同机动轨迹单元的情况下不同GRU隐层单元数对TSO-GRU-Ada预测性能的影响结果如图8所示。从图8中可以看出，随着GRU隐层单元数的增加，TSO-GRU-Ada模型的预测RMSE减小，预测时间增加；在相同隐层单元数下，21种机动轨迹单元的预测值RMSE与预测时间变化不大。综上分析，本文选取隐层单元数为20。

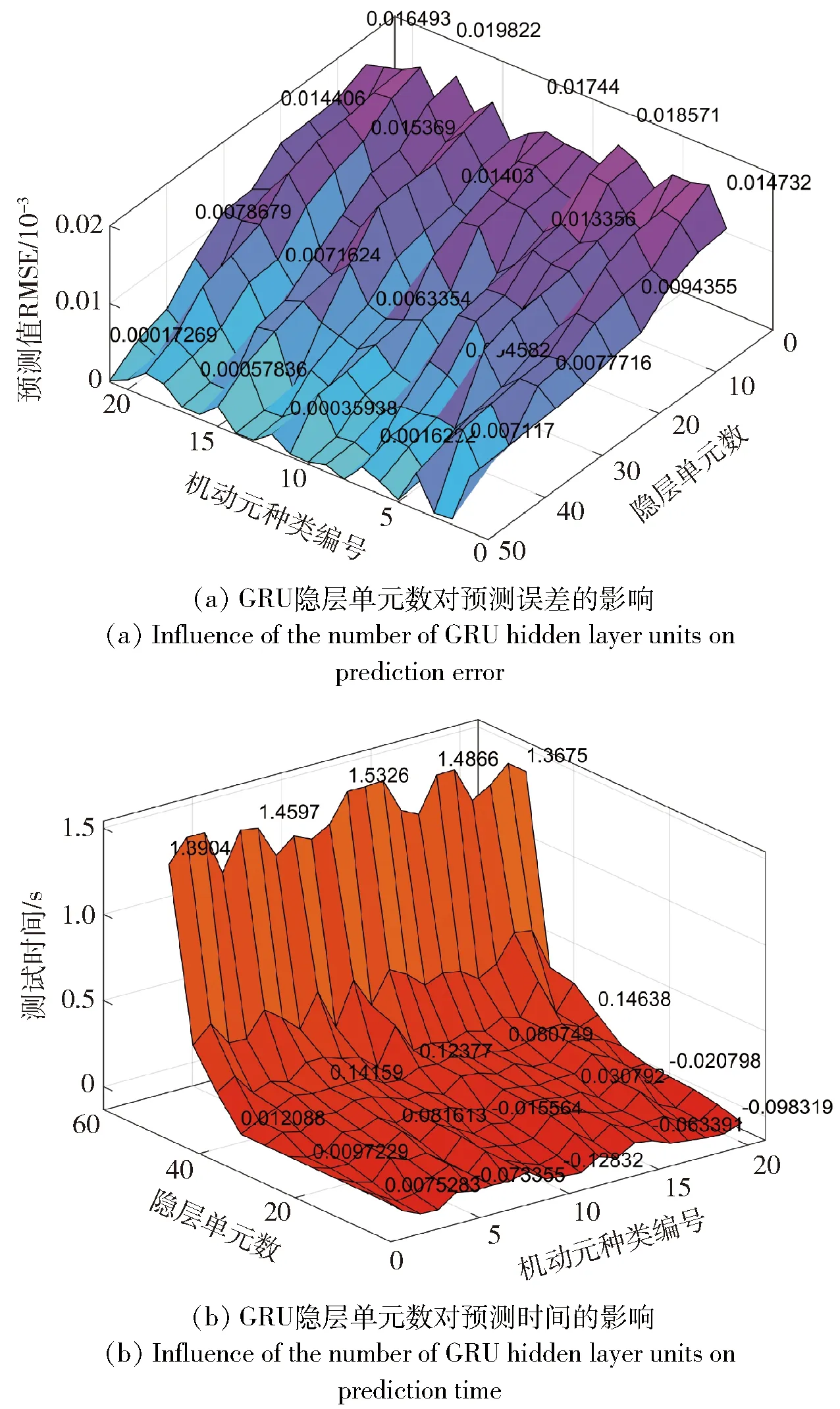
图8 不同隐层单元数对TSO-GRU-Ada预测性能的影响Fig.8 Effect of different hidden layer unit numbers on the prediction performance of TSO-GRU-Ada

4.2 机动单元预测仿真

根据TSO-GRU-Ada模型参数分析仿真实验，机动轨迹预测模型选取输入步长′=10，输出步长′=1，TSO-GRU-Ada选取8个弱预测器，TSO优化种群规模为25，隐层单元数为20。仿真实验的测试集由21种机动轨迹单元样本组成(每种机动轨迹单元有10个轨迹样本)，同时采用的是RMSE和预测时间作为预测性能的评价指标。表3给出了TSO-GRU-Ada与其他预测算法预测统计结果。从RMSE角度看，TSO-GRU-Ada算法在21种机动轨迹单元中表现最好，说明AdaBoost方法对提升预测精度有显著作用；TSO-GRU排名在GRU之前，表明TSO的优化效果显著。从预测时间角度来看，GRU的预测时间最短；由于TSO-GRU-Ada使用了集成器，预测时间是最长的，平均预测时间约为0.027 s，相比于0.1 s的采样时间能够满足实时性要求。

表3 TSO-GRU-Ada与其他预测算法预测统计结果比较

续表3

在水平面机动动作、垂直面机动动作和空间组合机动动作中各选取一种机动单元进行仿真验证。选取、和。为凹上爬升机动，为右转弯机动，为右转弯凸下飞机动。从图9(a)中可以看出：机动轨迹轴误差不超过44 m，轴误差不超过45 m，轴误差不超过45 m。从图10中可以看出，机动轨迹轴误差不超过13 m，轴误差不超过13 m，轴误差不超过11 m。从图11中可以看出，机动轨迹轴误差不超过3 m，轴误差不超过4 m，轴误差不超过37 m。综上分析，在3种不同类别机动单元中基于TSO-GRU-Ada的轨迹预测误差较小，满足精度要求。

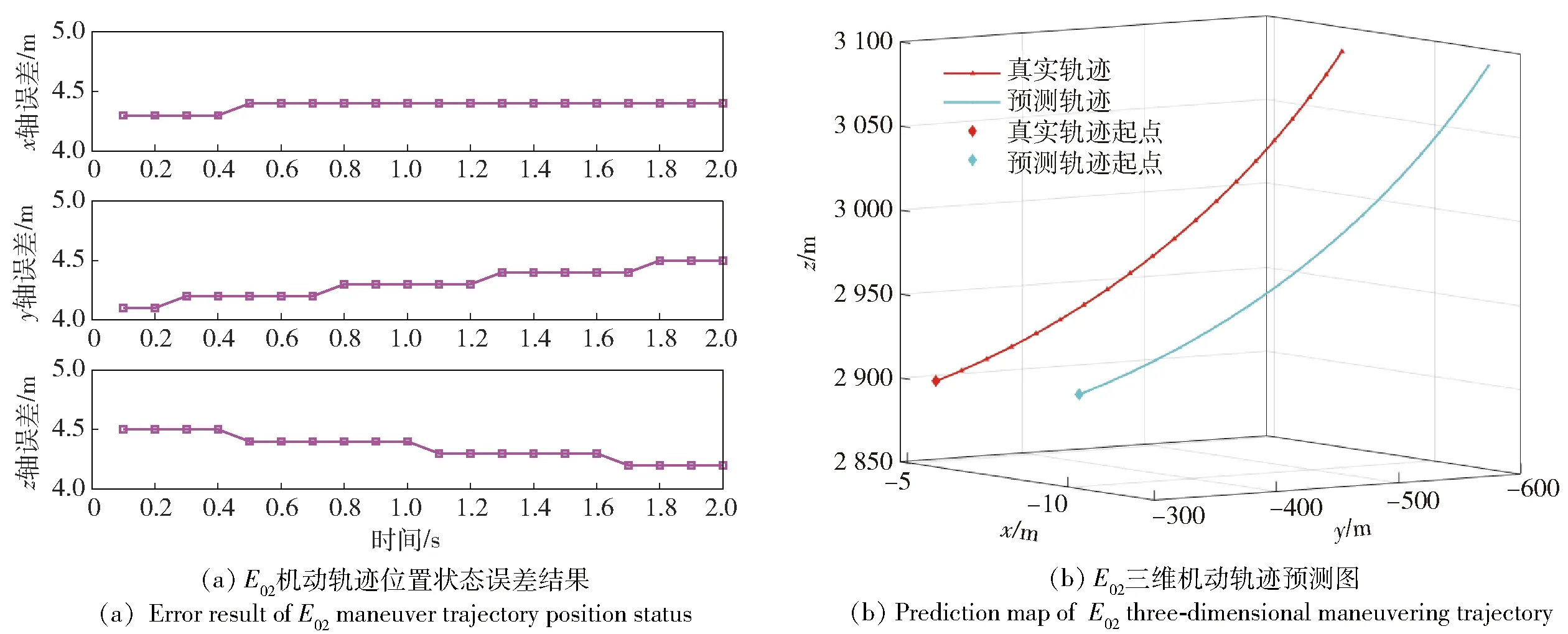
图9 机动轨迹单元E02的TSO-GRU-Ada预测结果Fig.9 TSO-GRU-Ada prediction results of maneuver trajectory unit E02

图10 机动轨迹单元E15的TSO-GRU-Ada预测结果Fig.10 TSO-GRU-Ada prediction results of maneuver trajectory unit E15

图11 机动轨迹单元E19的TSO-GRU-Ada预测结果Fig.11 TSO-GRU-Ada prediction results of maneuver trajectory unit E19

4.3 机动轨迹预测仿真

为验证本文所提方法在连续机动轨迹上的预测性能，从ACMI系统中挑选出一组机动轨迹，平均速度马赫数为0.75，分别与Elman、LSTM、GRU、TSO-LSTM、TSO-GRU算法进行预测对比，具体参数如表2所示。

从图12中可以看出TSO-GRU-Ada所预测的轨迹与真实轨迹基本重合，由图13可以看出本文算法在轴、轴和轴预测绝对误差都相对较小。表4通过平均绝对误差(MAE)和标准差(STD)评价预测的准确性与鲁棒性，在表4中可以直观看出本文算法在轴、轴、轴和总误差方面MAE均为最小，表明与对比模型相比本文模型的预测精度更高。同样本文模型具有较低的STD，相比于其他5种对比模型的鲁棒性能较好，但相对于机动单元预测，连续轨迹预测精度有所下降。

图12 机动轨迹三维预测图Fig.12 3D prediction of maneuver trajectory

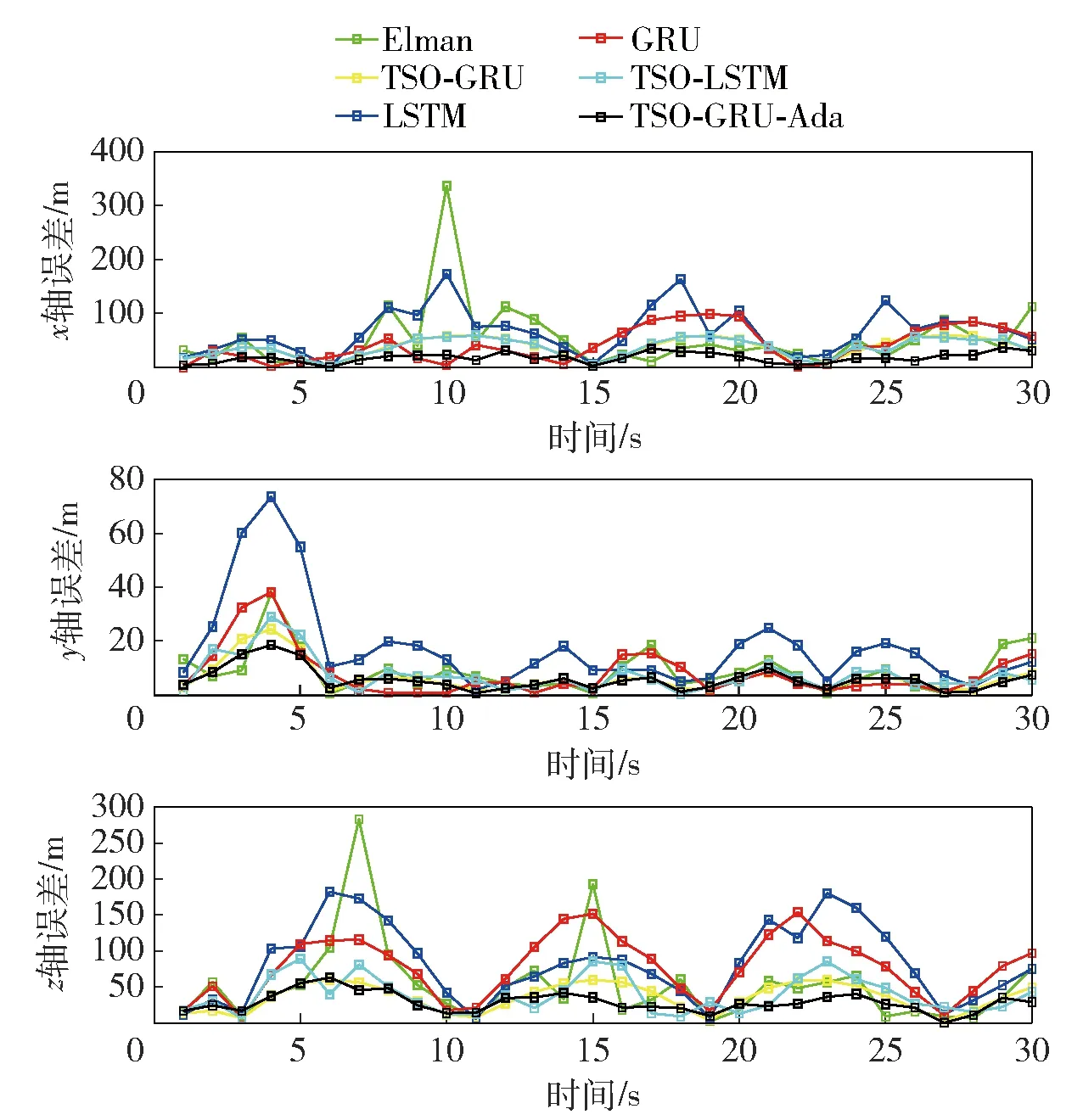
图13 轨迹预测误差Fig.13 Trajectory prediction error

表4 机动轨迹预测MAE统计结果

5 结论

本文在UCAV机动轨迹预测问题上建立UCAV 3自由度模型，解决了数据来源问题；创新性地利用机动轨迹特征参数建立机动单元库，将复杂轨迹划分为简单单元结构；介绍门控循环神经网络，并利用三角搜索优化算法更新网络内部权值和偏置，避免陷入局部最优。得到以下主要结论：

1)在不同机动单元中对TSO-GRU-Ada参数进行仿真实验，挑选出最优结构，选取参数分别为：种群规模25、基预测器个数′=8、隐层单元数20。

2)在21种机动单元情况下，TSO-GRU-Ada与Elman、LSTM、GRU、TSO-LSTM、TSO-GRU进行比较预测，结果表明其预测精度最高，且单步平均预测时间为0.027 s，满足预测时效性能。

3)在平均速度马赫数为0.75的连续机动轨迹情况下再次进行预测对比，预测精度较高且鲁棒性能较好，能够同时满足高预测精度和短预测时耗要求，但相对于机动单元预测，精度有所下降。

未来在连续机动轨迹预测上需要继续发展，进一步提高预测精度。