钨合金长杆弹撞击厚壁柱形目标临界跳飞角计算模型
金文, 门建兵, 蒋建伟, 彭嘉诚, 李梅
(北京理工大学 爆炸技术国家重点实验室, 北京 100081)
0 引言
目前,随着电磁炮等新型发射平台的发展,小口径杆式穿甲弹可用于防空反导领域执行防空拦截任务。由于传统火炮发射的杆式弹初速一般1 400~1 800 m/s,打击目标多为具有平板结构厚靶或多层靶装甲目标,而防空反导领域打击的目标多为具有柱面壳体结构目标,如GBU-31(V)3B/4B空地导弹战斗部采用厚度25 mm的特种合金钢壳体,这都对长杆弹毁伤能力提出了更高要求,而长杆弹与厚壁柱形目标在高速撞击时是否发生跳飞,是长杆弹能否有效毁伤来袭目标的关键问题。
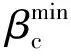
以上国内外学者主要集中于研究钨合金长杆弹撞击平面装甲目标时的跳飞规律,对于高速长杆弹撞击厚壁柱形目标的跳飞规律研究报道较少。而长杆弹作用于厚壁柱形目标易受着靶条件影响,发生跳飞时便无法对厚壁柱形目标形成稳定侵彻,进而无法侵入厚壁柱形目标造成更大毁伤效应。为确定长杆弹撞击厚壁柱形目标时跳飞的边界,需要建立长杆弹撞击厚壁柱形目标时临界跳飞角计算模型。
本文采用LS-DYNA3D显式动力学仿真软件,对不同着靶条件下钨合金长杆弹撞击厚壁柱形目标进行数值模拟,在此数值模拟结果基础上,引入着速、命中偏移角,建立基于Rosenberg模型的临界跳飞角修正计算模型。在已知长杆弹着速与命中偏移角条件下,能够预测其是否发生跳飞,对于评估长杆弹对厚壁柱形目标毁伤效果具有一定的指导意义。
1 几何模型与基本假设
长杆弹在具有一定命中偏移角,即以非理想状态撞击目标时,圆柱形壳体弧形结构无法保证稳定的着靶条件,长杆弹与目标靶板接触时的作用面不足以支撑长杆弹形成侵彻,从而跳飞。
截取厚壁柱形目标圆柱部区段用于小口径长杆弹撞击厚壁柱形目标计算分析。如图1(c)所示,过弹着点做目标圆柱体横截面,为两同心圆围成的平面。图1(a)中,弹芯轴线与横截面所夹锐角为着角;图1(b)中,临界跳飞角为长杆弹撞击靶板刚好发生跳飞时着角的大小(>,长杆弹跳飞;<,长杆弹侵彻);图1(c)为命中偏移角=0°时长杆弹与厚壁柱形目标作用位置示意图;在图1(d)中,为壳体厚度、为目标外径。定义弹芯轴线在横截面上投影与弹着点法线所夹锐角为命中偏移角,过圆心作平行于弹芯投影的直线,弹着点到距离为偏移距离。
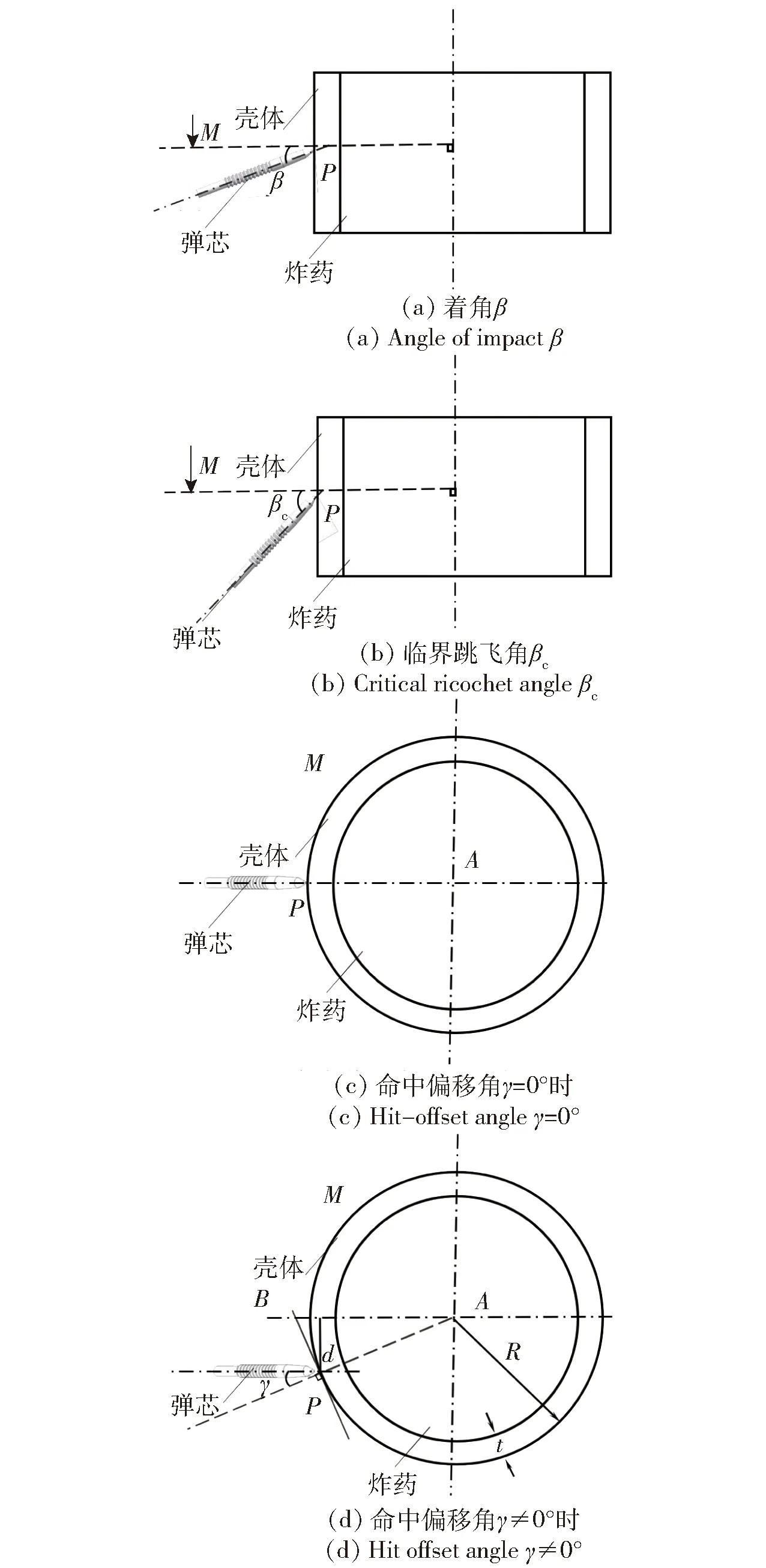
图1 几何模型参数示意图Fig.1 Schematic diagram of parameters for the geometric model
图2为Lee模型与Rosenberg模型对比结果。Lee等基于Rosenberg研究了靶板厚度对临界跳飞角影响。对于薄靶而言,临界跳飞角值增大4左右,因此本文中假设壳体厚度对临界跳飞角影响可以忽略;对于厚壁柱形目标半径,与命中偏移角关系为sin=(=1),则sin的物理含义为:对于具有任意半径的厚壁柱形目标,长杆弹撞击位置的相对偏移程度。

图2 Lee模型[11]与Rosenberg模型[9]对比Fig.2 Lee model[11] versus Rosenberg model[9]
结合Rosenberg等研究结果,当长杆弹以着速作用于厚壁柱形目标时,临界跳飞角可表示为关于着速、长杆弹材料密度、靶板侵彻阻力、弹体头部速度、命中偏移角、壳体厚度、目标半径的函数:
=(,,,,,,)
(1)
式中:、均为与弹靶材料相关常数;弹体头部速度=0 m/s;目标半径可由命中偏移角表征。
在上述基础上提出以下基本假设:
1)Rosenberg模型适用于小型长杆弹撞击厚壁柱形目标时临界跳飞角计算,不考虑长径比等因素对计算模型的影响;
2)忽略壳体厚度对临界跳飞角影响,弹体头部速度=0 m/s,命中偏移角可表征厚壁柱形目标半径对临界跳飞角影响;
3)长杆弹与厚壁柱形目标材料均匀性好,且在二者相互作用下其材料强度不发生变化;
4)厚壁柱形目标内部装药为惰性材料,暂不考虑炸药装药起爆及炸药类型对临界跳飞角影响。
基于上述假设条件建立修正项,将着速、命中偏移角作为对临界跳飞角影响的主要表征量。引入Alekseevskii模型中的弹尾临界速度:
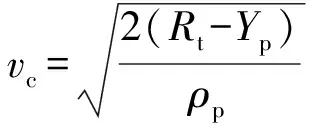
(2)
式中:为长杆弹屈服强度。假设、二者间相互独立,且、对临界跳飞角的影响效应可线性叠加;定义=为长杆弹撞击厚壁柱形目标时相对于修正前的临界跳飞角的修正因子。
综上,选取尾临界速度为基本量,根据量纲分析π定理对自变量进行无量纲化处理,(1)式可表示为

(3)
式中:为着速与弹尾临界速度的比值;
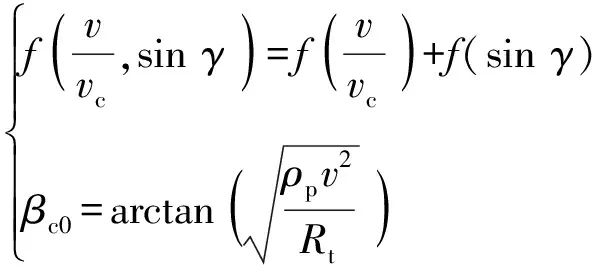
(4)
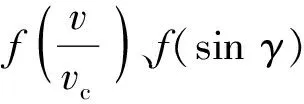

(5)

(6)
、分别为特定命中偏移角和着速。
以上为基于Rosenberg计算模型应用于厚壁柱形目标几何模型的修正模型建立方法。
2 修正计算模型
Tate等建立的临界跳飞角预测计算模型为
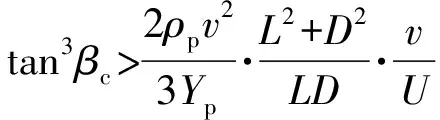
(7)
式中:为长杆弹弹长;为长杆弹直径。
Rosenberg等在Tate研究基础上提出将非对称力仅作用于弹体由于撞击所侵蚀的质量上,避免了计算模型中出现杆长度项:

(8)
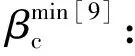
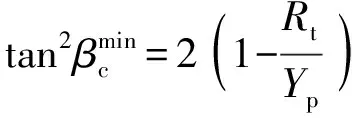
(9)
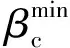

2.1 修正数据获取
采用LS-DYNA3D显式动力学软件进行数值模拟计算,选用Solid164六面体Lagrange单元算法,采用常见长杆式穿甲弹中经常应用啮齿式结构;长杆弹与壳体之间采用侵蚀接触能更好的模拟长杆式穿甲弹穿甲过程中弹体破碎和侵蚀过程;长杆弹、壳体与炸药之间均采用侵蚀接触,并添加材料侵蚀关键字对炸药单元进行约束。如图3所示,具有轴对称性质的工况建立其1/2有限元模型以减少计算时间,非轴对称工况采用全模型建模。
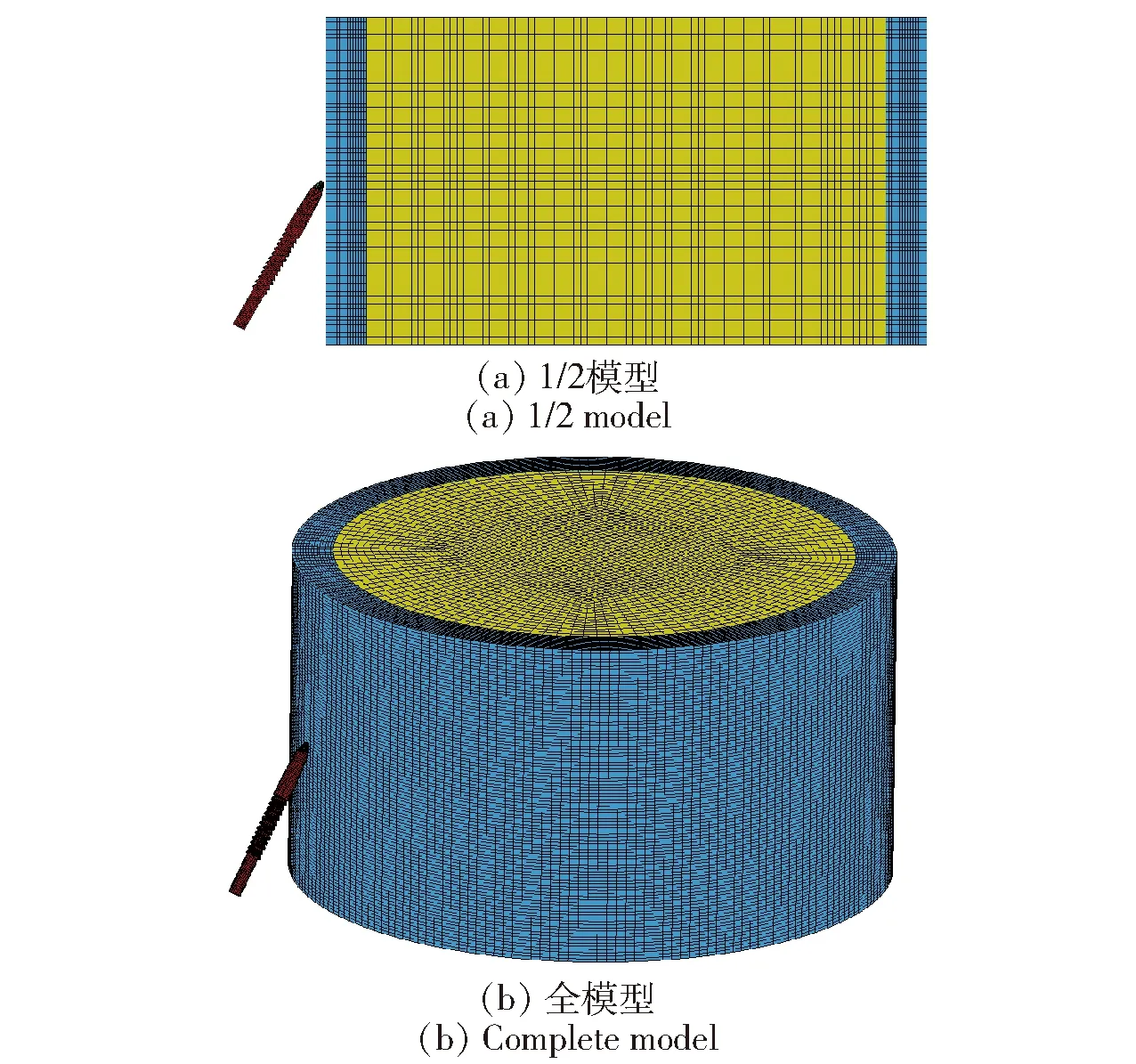
图3 弹靶作用有限元模型Fig.3 Finite element model of the projectile impacting the target
*MAT_ELASTIC_PLASTIC_HYDRO材料模型用于模拟钨合金长杆弹在穿甲过程中发生的弹体侵蚀和破碎现象,采用Gruneisen状态方程,长杆弹材料参数参考文献[18]所用参数;靶板材料为30CrMnSiNi2A,内部装药采用惰性材料模型*MAT_PLASTIC_KINEMATIC表征。钨合金、装药材料参数如表1、表2所示。
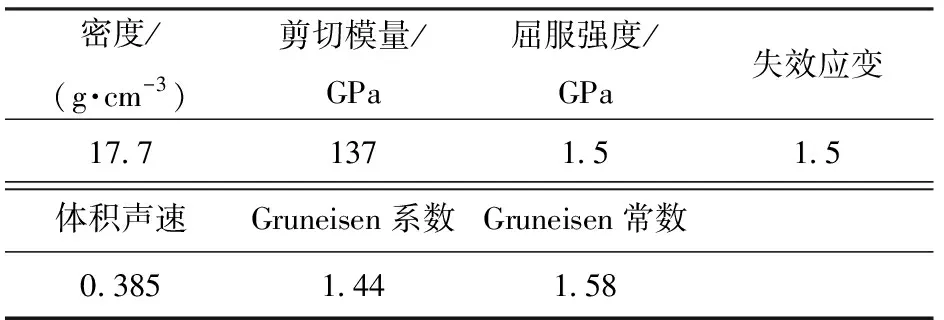
表1 钨合金材料参数

表2 装药材料参数
对数值模拟计算模型的正确性进行验证。Rosenberg等建立的临界跳飞角计算模型中,临界跳飞角只与弹靶材料特性有关,与其他因素无关。如图4、图5所示,设立对照数值模拟工况,着速=1 000 m/s,靶板沿法线方向速度270 m/s,着角53°时数值模拟结果跳飞状态与Rosenberg等的试验结果比对,其结果基本一致。在此基础上,进一步研究长杆弹侵彻厚壁柱形目标时临界跳飞规律。

图4 典型条件下数值模拟结果Fig.4 Numerical simulation result under typical conditions

图5 典型条件下试验结果[10]Fig.5 Experimental result under typical conditions[10]
首先根据(9)式对临界跳飞角进行初步预估,然后通过升降法逐渐逼近,最后确定临界跳飞角区间,当区间足够小时,可取区间极限平均值作为数值模拟计算估计值。考虑到计算能力的有限性,以相邻两不同着速、+1进行数值模拟,得到的临界跳飞角可能处于同一区间,此时利用着速+2对速度区间[+2]近似线性估计,以确定着速时临界跳飞角估计值。表3为着速为1 800 m/s时在临界跳飞角区间为[70° 75°]时的侵彻过程图。由表3对比可知,该速度下以70°着角侵彻厚壁柱形目标时,对比75°着角能够形成明显的侵彻过程——当着角为75°时,靶板法线与长杆弹轴线夹角逐渐增大,最后甚至趋于90°。

表3 着角为70°、75°各时刻侵彻状态
2.2 修正函数建立
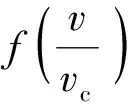
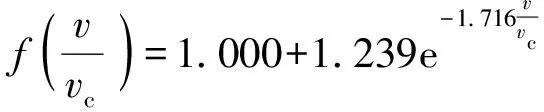
(10)
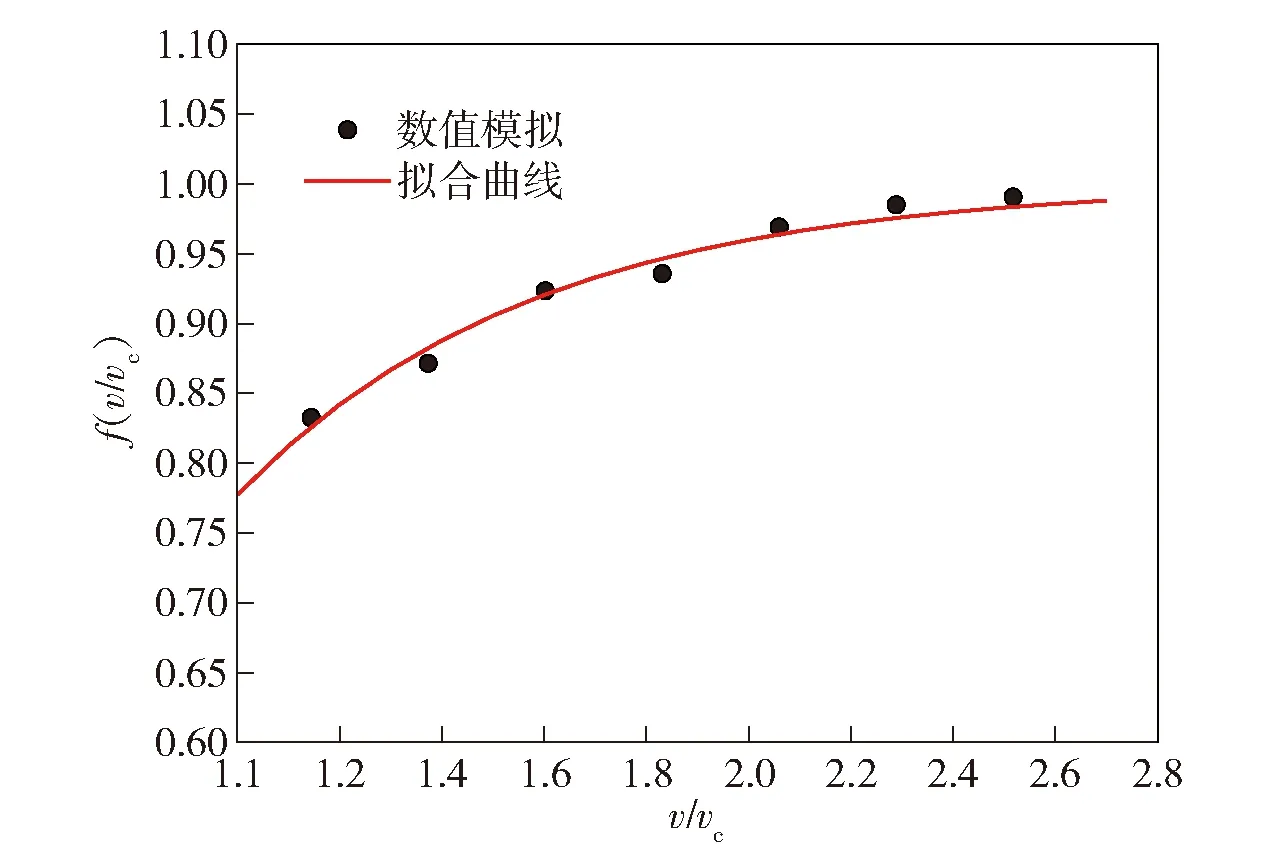
图随着速变化曲线 curve with impact velocity

图7为不同命中偏移角下(sin)值,以及(sin)随sin变化的拟合曲线。
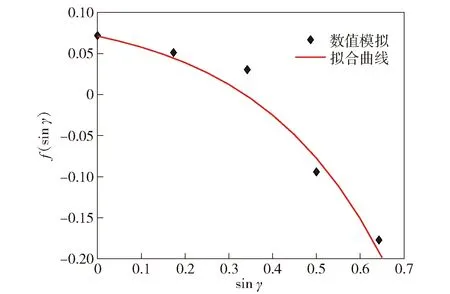
图7 f(sin γ)随命中偏移角γ变化曲线Fig.7 f(sin γ) curve with hit-offset angle
当=0°时,不考虑命中偏移角对临界跳飞角的影响,此时
(sin)=0
(11)
图7中随着命中偏移角的增大,长杆弹形成稳定侵彻厚壁柱形目标的能力急速弱化,图中拟合曲线表达式为
(sin)=0104 3-0033 10e3406sin
(12)
综上,参考Lee等的研究方法,关于命中偏移角的修正因子函数形式为=+e形式。对命中偏移角进行无量纲化后,得到拟合曲线方程中各参数如表4所示。

表4 拟合曲线方程参数
将(10)式、(12)式代入(3)式、(4)式,可得到长杆弹撞击厚壁柱形目标时临界跳飞角的修正计算模型。
当=0°时:

(13)
当0°<≤40°时:

(14)
式中:命中偏移角可由交汇条件与目标结构决定,即用柱形目标半径、命中偏移距离表示:
=arcsin ()
(15)
图8为临界跳飞角随撞击速度以及命中偏移角分布图,可见长杆弹临界跳飞角随撞击速度与命中偏移角的减小呈辐射状减小。若定义长杆弹在典型弹目交汇条件(即=60°)作为过渡区,则可将图8分为3大区域:
1)侵彻区:此区域内临界跳飞角在65°以上。这一区域内影响临界跳飞角变化的主导因素为着速,随着速增大,临界跳飞角受命中偏移角影响逐渐减弱,长杆弹着角支持其形成稳定侵彻;
2)过渡区:此区域内临界跳飞角在60°左右,作为侵彻区与跳飞区的过渡区域;
3)跳飞区:这一区域内影响临界跳飞角变化的主导因素为柱形目标弧形壳体结构,即随着命中偏移角的增大,临界跳飞角受着速影响逐渐减弱,长杆弹着角并不能支持其形成侵彻,发生跳飞现象。
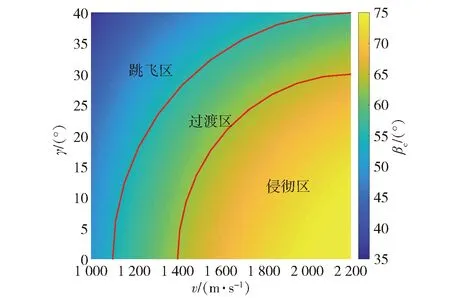
图8 临界跳飞角分布Fig.8 Distribution of the critical ricochet angel
3 模型校核
图9为命中偏移角=30°时各着速下长杆弹的着靶状态与Rosenberg计算模型和修正计算模型对比图。此时临界跳飞角变化趋势与Rosenberg等计算模型基本一致;临界跳飞角随着速增大而逐渐增大,最终趋于平缓;命中偏移角的存在大大减小了临界跳飞角,并且随速度增加,命中偏移角的影响程度逐渐降低。仿真结果中跳飞与侵彻数据点较为一致地分布于修正计算模型两侧。
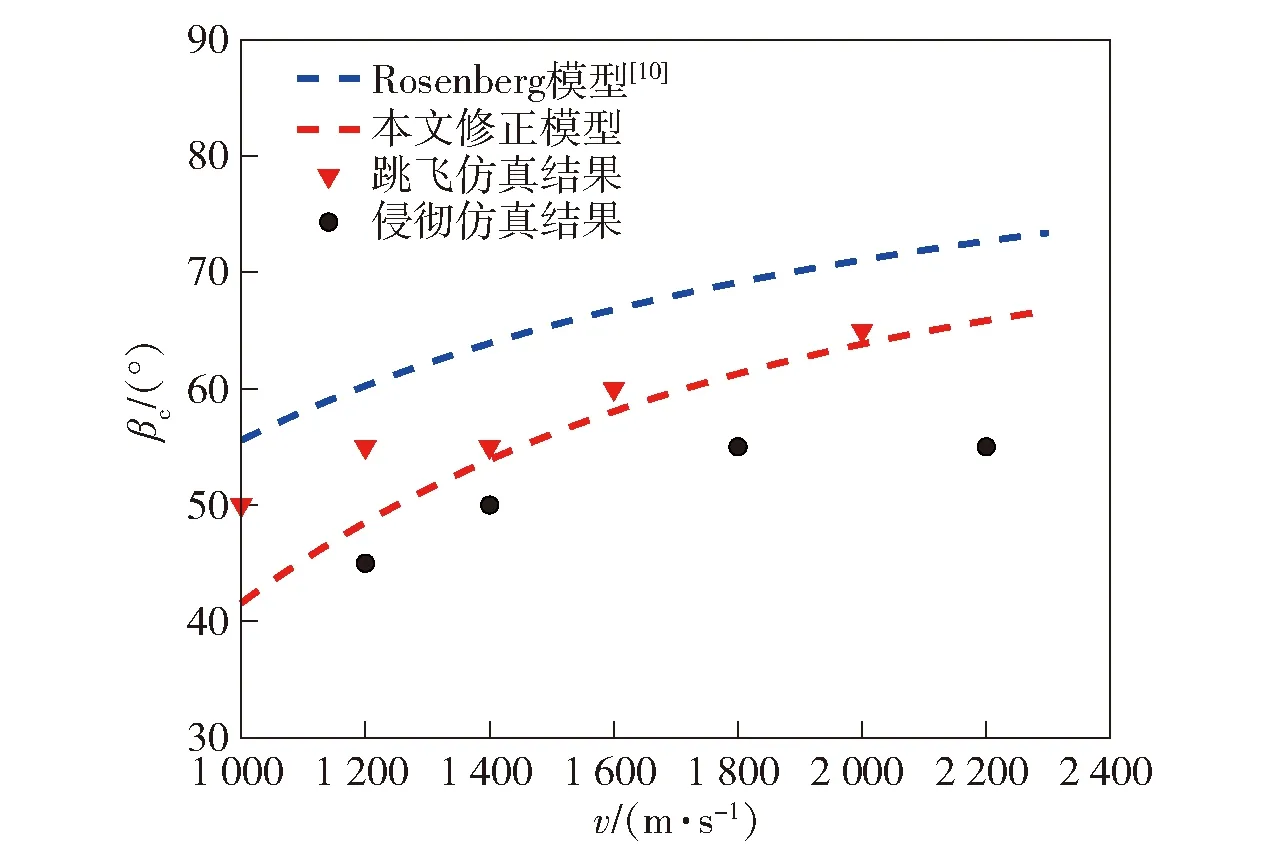
图9 γ=30°时修正前后计算模型与数值模拟结果校核Fig.9 Verified computational model and numerical simulation results before and after correction when γ=30°
选取不同着速、命中偏移角、着角进行数值模拟。图10为任取命中偏移角、着速时,数值模拟数据点分布于该临界跳飞角修正计算模型所形成的分界面上下两侧,较好地区分了侵彻- 跳飞。因此,该计算模型能够准确反映长杆弹撞击厚壁柱形目标时跳飞的边界,具有一定准确性与适用性。

图10 侵彻- 跳飞分布Fig.10 Penetration-ricochet distribution
4 结论
本文针对不同着靶条件下钨合金长杆弹撞击厚壁柱形目标的跳飞问题,基于经试验验证的数值模拟手段,量化分析着速、命中偏移角与临界跳飞角关系,建立确定钨合金长杆弹撞击厚壁柱形目标跳飞边界的工程计算模型,可作为实际工程参考。得出以下主要结论:
1)采用数值模拟方法,通过对长杆弹以不同着靶条件撞击厚壁柱形目标进行仿真计算,获得着速取值为1 000~2 200 m/s的钨合金长杆弹撞击厚壁柱形目标时的临界跳飞角,数值模拟结果与Rosenberg等的仿真、试验结果基本一致。
2)引入包含着速、命中偏移角的修正因子,对Rosenberg临界跳飞角计算模型进行修正,并构造钨合金长杆弹撞击厚壁柱形目标时临界跳飞角计算模型。
3)基于不同着靶条件下的数值模拟结果,对钨合金长杆弹撞击厚壁柱形目标时临界跳飞角计算模型进行校核验证,校验结果表明,此计算模型具有一定普适性与准确性。

