基于MC-XGBoost模型的航空发动机振动特性预测

梅 潇，池华山，岳 聪，范建瑜，刘宗沁

(上海海事大学 物流工程学院，上海 201306)

航空发动机作为高端制造业的顶尖产品，不但制造工艺要求严苛，而且还会受到恶劣的工作环境制约。装配作为航空发动机的制造终端，它的质量很大程度影响着其工作性能表现。高压转子组件由大量精密零部件装配而成，又是航空发动机的核心部件，对装配质量要求极高。如果转子组件装配方案设计不合理、几何/不平衡量过大，必然会给整机带来复杂且难以解决的振动问题，直接影响发动机服役性能[1-2]。

涡扇发动机的高压转子组件主要由高压压气机(high pressure compressor,HPC)与高压涡轮(high pressure turboe,HPT)两部分组成，在组装完这两部分后还会加上篦齿盘密封。为提高转子系统的装配效率，减少现场的调试和试装工作，学者们做了很多工作。Zhang等[3]从装配误差的角度出发，研究了航空发动机多级转子测量装配设备的测量误差传播原理，分析了导轨直线运动和转台旋转运动对最终找准误差的影响。孟亮国等[4-5]针对航空发动机高压转子装配精度的预测与堆叠问题，考虑同轴度的影响因素，提出了一种转子装配定心误差与相对偏斜误差的预测方法。余坚等[6]采用分形方法对连接转子振动试验结果进行分析，发现动态响应信号的盒维数是检测装配振动的一个很好的指标。以上方法只是基于单独的转子装配或振动问题，没有将两者综合分析。

由转子的装配到整机的振动并不是简单的线性关系，而是复杂的非线性关系，为研究两者的关系使用了一种基于分类和回归树算法(classification and regression trees,CART)的集成算法模型极端梯度提升(eXtreme gradient boosting,XGBoost)。CART算法最初是由Brieman等[7]在1984年提出。随着近几年机器学习热潮的掀起以及对CART算法的深入研究，越来越多的改进算法模型被提出，如随机森林(random forest,RF)[8]，梯度提升树(gradient boosting decision tree,GBDT)[9]，以及2016年Chen等[10]提出了基于GBDT改进的XGBoost机器学习算法模型。这些算法模型的核心还是CART，但是它们将CART集成化，从而提高了计算精度与效率。

近年来，XGBoost模型在各个工程领域得到了广泛的应用。李卫星等[11-14]将XGBoost模型用于故障诊断，均取得了不错的预测效果。王伟等[15]将XGBoost模型用于预测热镀锌钢卷力学性能，得出94.6%的数据样本相对误差在6%范围内，具有很高的预测精度。陈振宇等[16]使用XGBoost来对电力系统负荷进行预测研究，他们将XGBoost模型与LSTM (long short term memory network)模型相结合，并对实际电力负荷数据进行了算例分析，结果表明所构建的LSTM和XGBoost组合预测模型的平均百分比误差为0.57%。然而XGBoost模型在实际应用时很容易产生过拟合现象，即模型在训练集上会拟合所有的输入参数，而实际上很多输入参数会导致输出结果与实际结果偏差变大，它需要对模型的输入参数进行限制。

本文从装配过程中的装配数据与整机测试过程中振动数据出发，通过不平衡响应振动方程描述了装配阶段几何偏差和不平衡偏差与振型的机理关系，提出基于Breiman等[17]的最大相关性(maximum correlation,MC)系数与XGBoost模型的改进模型，称其为MC-XGBoost预测模型，建立某型航空发动机高压转子组件装配参数与整机振动参数的数学分析模型。通过实测样本的训练和预测并与RF、GBDT算法模型进行预测结果对比，以验证本文方法的计算精度和预测准确性。

1 转子组件与组合转子不平衡量的转换关系推导

如图1为高压转子的不平衡量转换关系示意图。图1中：O为转子组件(HPT或HPC)的设计回转中心;O′为转子组件的几何形心;O″为由转子组件HPC与HPT装配得到的组合转子的回转中心，转子组件与组合转子的回转中心之间在端面有一个很小的投影角度，在实际装配过程中这个角度很小在这里可以忽略不计；ds为转子组件回转中心O到几何形心O′的几何偏心；σ为角度；p′为转子组件相对于其质心C的偏心距；θ′为角度；dt为转子组件形心O′相对于组合转子O″的几何偏心；λ为角度。可根据矢量关系推导出最后的组合转子回转中心O″相对于转子组件质心C的偏心矢量p″。

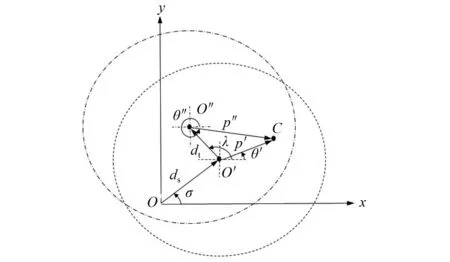
图1 转子不平衡量转换示意Fig.1 Diagram of rotor unbalance conversion

(1)

根据式(1)中转子组件几何偏心矢量与组合转子几何偏心矢量的关系，把转子组件的不平衡量转换到最终组合转子上并将其定义为U，可由式(2)表示。

Tm′(p′-dt)=U

(2)

式中：U=p″m″，m″为组合转子的偏心质量；m′为转子组件的偏心质量；T为转子组件与组合转子之间关系的转换系数。

根据转子动力学理论，转子的任意不平衡量可以按转子的模态振型展开，组合转子的工作转速介于第一阶、第二阶临界转速之间，所以可以只考虑前两阶的模态不平衡，把组合转子在稳态下的不平衡量U按前两阶振型展开。

Ueiθ″=V1eiα1+V2eiα2

(3)

式中：V1,α1分别为第1阶振型的振动幅值与相位角；V2,α2分别为第2阶振型的振动幅值与相位角；U,θ″分别为不平衡矢量U的大小和方位角。

从式(2)、式(3)的等量关系可以看出，转子组件的不平衡量U、几何偏心dt与组合转子的振动幅值V存在一定的关系，所以考虑从高压转子装配过程中的装配数据与测试过程的整机振动响应数据角度分析两者的关系。

2 数据来源说明

如图2为某型涡扇发动机高压转子的结构示意图，高压转子包括HPC与HPT两部分，其装配过程首先需要装配好HPC与HPT组件，再将HPC与HPT组件按连接面装配成高压组合转子。在高压转子的装配过程会记录一些重要的装配参数，包括动平衡参数与几何参数，如表1所示。

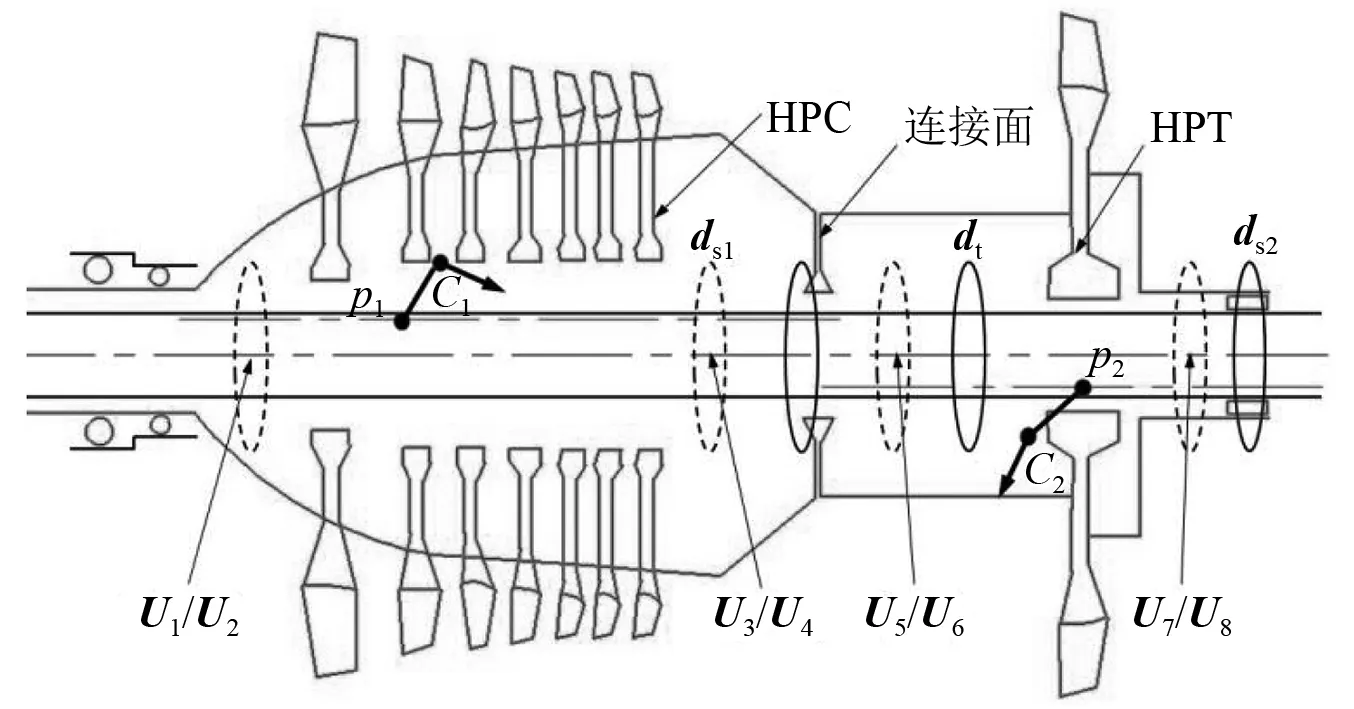
图2 高压转子结构示意Fig.2 High-pressure rotor structure diagram

表1 装配参数说明Tab.1 Description of assembly parameters

动平衡装配参数中不平衡量包括试车前初始不平衡量与校正后的最终不平衡量，而不平衡矢量作为HPC质心C1、HPT质心C2偏移的主要装配性能参数，包括不平衡量大小和方向两个子参数，对其统一用不平衡矢量U表示。几何参数测量过程中需将被测件竖立，分别测量HPC与HPT组件以及组合转子的几何偏心矢量。

高压转子装配完成后，会安装到发动机上进行整机的试车，试车时在发动机的机匣上布置3个加速度传感器记录发动机在稳态转速下的振动响应。对所采集的加速度信号，在信号处理过程会将加速度信号通过积分变换的形式转换为振动速度，再将所获振动速度用3个振动参数表示，其中振动参数V1是中介机匣水平测点的振动速度峰值，振动参数V2是中介机匣垂直测点的振动速度峰值，振动参数V3是低压涡轮机匣垂直测点的振动速度峰值。

将实测的多组某型航空发动机高压转子所有装配参数当成输入变量矩阵X=[U1,U2,…,dt]，所有振动参数当成输出变量矩阵Y=[V1,V2,V3]。

3 数学模型与方法

为研究高压转子装配过程的不平衡量、几何偏心与测试过程整机振动响应的数学表征关系，本章将建立一个MC-XGBoost预测模型并介绍模型预测精度的评估指标。

3.1 MC-XGBoost建模原理

用Y表示输出变量即试车振动参数，X为输入变量即装配参数，首先将所有变量归一化，对于任意给定的一对随机变量(X，Y)，X和Y之间的MC系数记为ρ*，其计算如下

(4)

式中:ρ为皮尔森相关系数;θ和φ为Y和X的波莱尔可测函数;用θ*和φ*表示可获得MC的最优转换。

式(4)的最优转换θ*和φ*可通过式(5)的优化问题获得。

(5)

式中：P为(X,Y)的联合分布；L2(P)为在P下平方可积函数，令e*2为e2的最小值。

最小优化问题式(5)与式(4)是等价的，对式(5)可以采用样条估计求解，最终得到X与Y的MC系数估计λ。

(6)

式中,A00,AXX,AX0和A0X为n维随机变量X与Y转换到标准B样条基上的估计值矩阵。

λ的取值范围为[0,1]，其等于1时认为随机变量X和Y之间存在直接的线性或非线性关系。当其不等于1时，只能从其数值大小的排序关系出发，判断两组随机变量间相关性强弱。

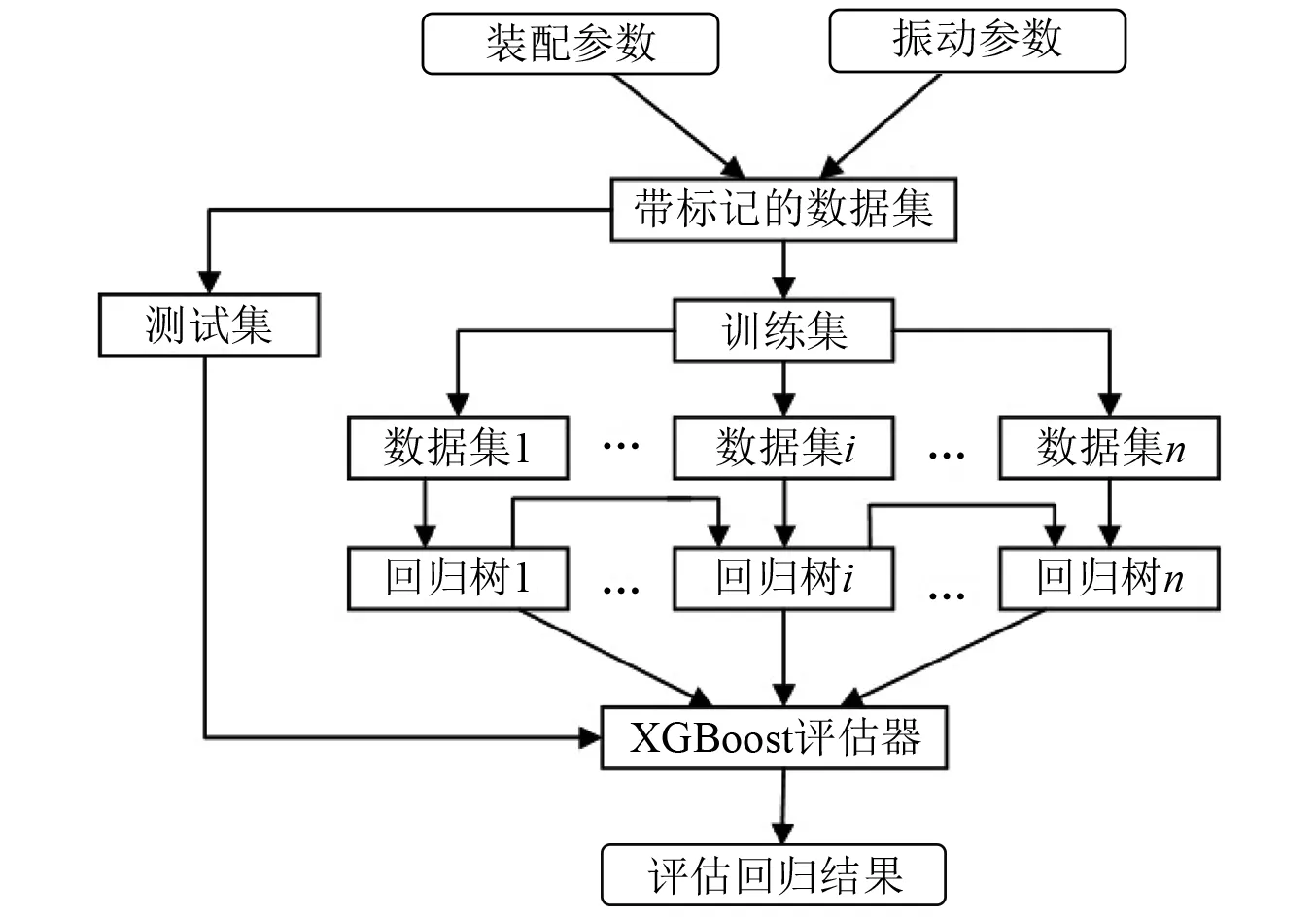
图3 XGBoost模型建模原理Fig.3 XGBoost model modeling principles

(7)

如图4为MC-XGBoost模型的建模原理，对所有的输入变量X与输出变量Y所组成的数据集{X,Y}。首先计算所有输入变量X与输出变量Y之间的MC系数λ，根据MC系数排序筛选合适的输入变量组成数据集X′。再将选择的输入、输出变量组合的数据集{X′,Y}划分为训练集与测试集，把训练数据集代入XGBoost模型中进行输入变量X′与输出变量Y之间潜在规则的学习耦合。最后把测试集代入已经耦合好训练集所表现出一定回归规则的XGBoost模型中评估模型的耦合效果，若模型预测结果的R2<0.4,则表明模型预测精度太低，所用的输入变量X′并不是输出变量Y的敏感源，需要再根据相关性系数λ调整输入变量X′进行预测。

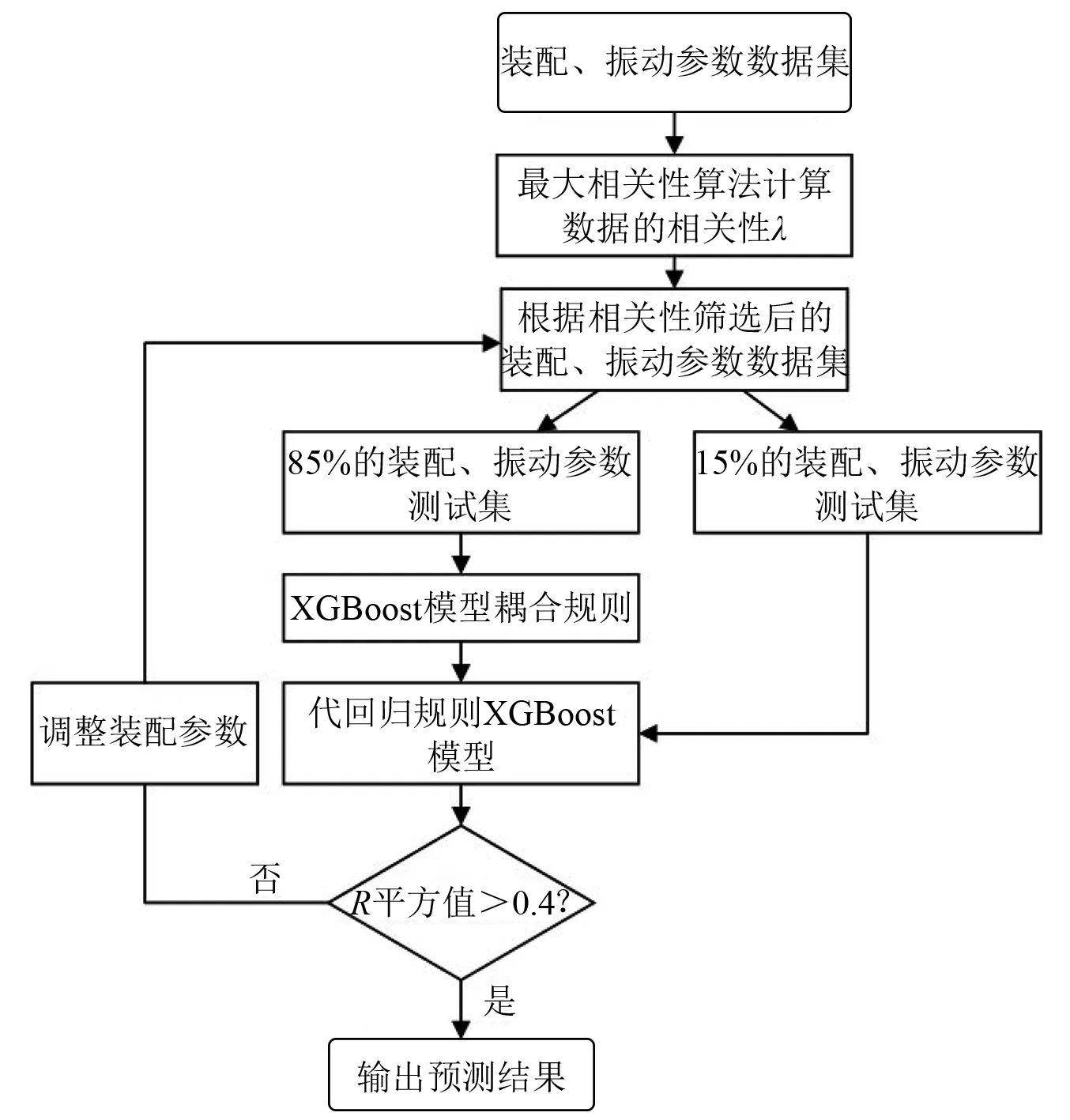
图4 MC-XGBoost模型建模原理Fig.4 MC-XGBoost model modeling principles

(8)

因此，根据XGBoost算法得到输入变量X′与输出变量Y的目标优化函数，如式(9)所示。

(9)

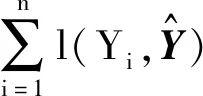
(10)

式中：T为输入变量与输出变量耦合的回归树的叶子结点个数；ω为回归树的叶子节点分数；γ的用途为控制回归树的叶子结点个数；α用于防止回归树的叶子节点分数过大。模型的迭代采用叠加式的训练的方式以进一步最小化目标函数。每次迭代将目标函数更新为

(11)

将式(11)在ft(X′i)=0处泰勒展开到二阶得到

Ω(ft)

(12)

去除式(12)中的常数项，得到

其中，

上述式(13)可以看成是关于叶子结点分数ω的一元二次函数，对其求解得到。

(14)

于是得到最终的输入变量X′与输出变量Y的目标优化函数为

(15)

其中，

3.2 模型评估指标及其取值说明

为更好的评判模型对测试集的预测精度，引入评判指标均方误差(mean squared error，MSE)与R2，R2的定义如下

(16)

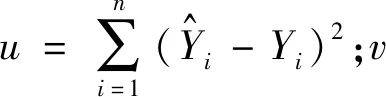
R2的范围为[-∞,1]，如果模型预测效果很好，其R2值就会接近于1，如果模型预测结果偏差大，模型的残差平方和远远大于模型的总平方和，R2就会为负。

实际航空发动机振动响应的影响因素繁杂，本文仅是从其高压转子的装配参数角度进行分析，考虑到由高压转子到整机的装配过程还会产生装配偏差，以及高压转子到整机机匣各个测点会有振动传递的损失，其传递过程也有其他振动激励的加入，综合考虑之后将模型预测精度的衡量标准R2值取为大于0.4。

4 MC-XGBoost模型预测与分析

针对实测的120组某型航空发动机高压转子的装配参数X与测试过程整机振动响应参数Y数据样本，使用本文提出的MC-XGBoost模型研究高压转子装配过程的不平衡量、几何偏心与其试车振动的关系。首先列出了模型最终筛选的各个振动参数的重要装配参数。然后与原始的XGBoost模型的预测效果进行对比。最后，针对振动参数V1将MC算法与RF模型、GBDT模型相集合并与原始的RF、GBDT对比。对所有的模型，均使用85%的数据用做模型的训练集，剩下的数据用作测试集，测试并对比各个模型的预测精度。

4.1 装配参数评价筛选

对实测的装配参数X与试车振动参数Y，首先计算其MC系数λ，再根据λ大小进行排序，以振动参数V1为例，所得的相关性最强的前5位装配参数排序如表2所示；然后使用MC-XGBoost模型对不同的振动参数筛选合适的装配参数数据集X′，对3个振动参数得到的最终装配参数如表3所示。MC-XGBoost模型最终筛选的装配参数都包含组合转子的几何偏心大小|dt|，它是组合转子的最终检验标准，是造成整机振动的一个重要因素。振动参数V1与振动参数V2都是中介机匣位置的振动速度峰值，所以其振动敏感源一致均为HPT的初始不平衡量大小与组合转子的几何偏心大小|dt|。振动参数V3是低压涡轮机匣的振动速度峰值，其振动敏感源相对于中介机匣测点略有不同。

表2 振动参数V1相关性最强的前5位装配参数Tab.2 The top 5 assembly parameters with the strongest correlation with vibration parameter V1

表3 各个振动参数的预测参数Tab.3 Predictive parameters of each vibration parameters

4.2 MC-XGBoost模型其他模型预测结果对比

将所有的装配参数作为模型的输入，振动参数作为模型的输出，即用装配参数代入模型来预测振动参数。使用XGBoost模型与MC-XGBoost模型分别预测振动参数，得到如图5的预测值与实测值对比与如表4的误差对比。

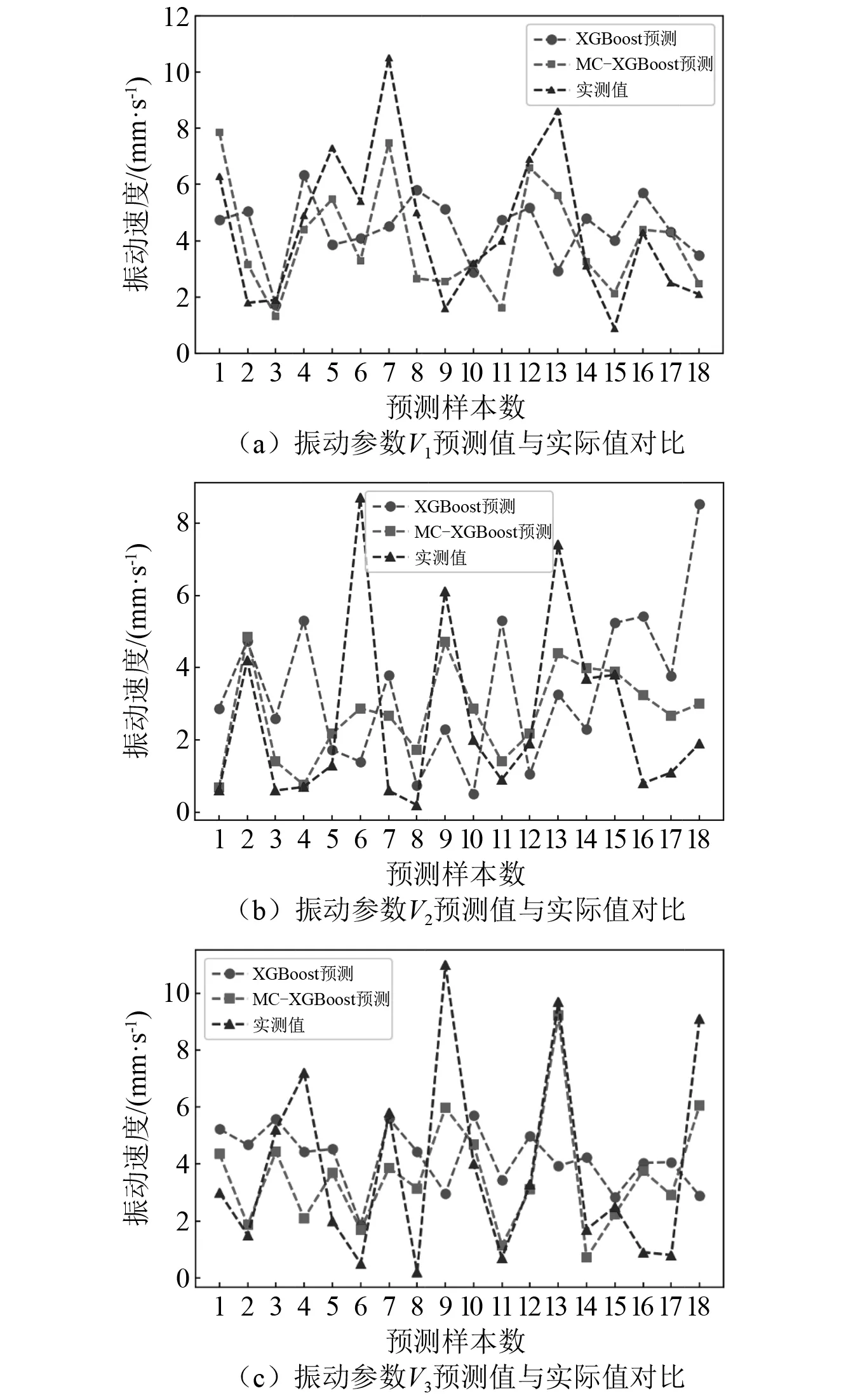
图5 不同振动参数的预测值与实际值对比Fig.5 Comparison between predicted and actual values of different vibration parameters

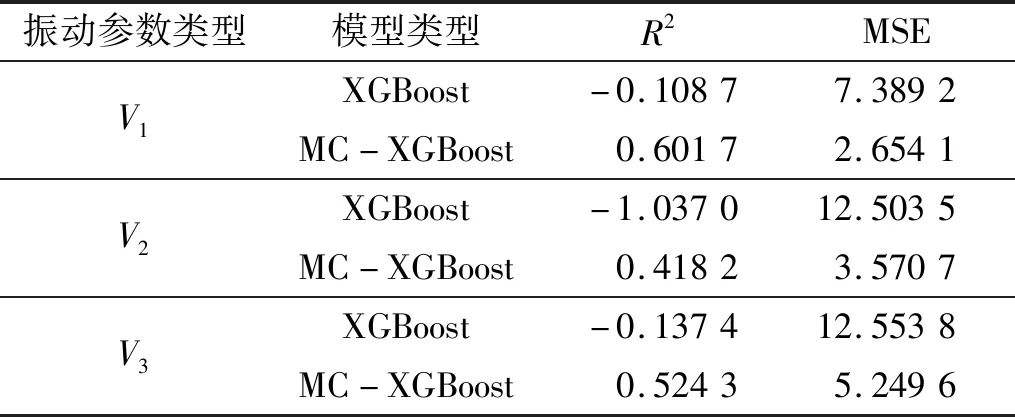
表4 各振动参数误差Tab.4 Error of each vibration parameter

由表4可知，使用XGBoost模型来分别预测3个振动参数，其R2全为负值，这说明模型预测偏差很大。使用MC-XGBoost模型进行预测，其R2全为正值且大于0.4，表明模型预测效果明显提升，特别是对于振动参数V1与振动参数V3，如图5(a)、图5(c)所示，预测的效果发生了质的提升，然而对于振动参数V2的预测偏差还是较大，如图5(b)所示，但是相比于XGBoost模型，其预测精度明显提升。

从表4中两模型的MSE值也可知，MC-XGBoost模型的MSE值普遍比XGBoost模型的小，这说明MC-XGBoost模型的预测结果偏差普遍比XGBoost模型小。

所介绍的MC算法作为计算数据间相关性算法的一种，它也可以与其他机器学习算法模型如RF、GBDT结合起来使用。

按照相同的方式将参数变量代入RF、GBDT、MC-RF、MC-GBDT模型中，以振动参数V1为输出，得到如表5所示的各模型误差对比。由表可知，RF、GBDT模型的R2值都比MC-RF、MC-GBDT的小，说明其预测结果都不如加上MC系数后效果好，这说明了装配参数优化选择的必要性。

对比表5中RF、MC-RF、GBDT、MC-GBDT模型对振动参数V1的预测精度，可以看出MC-XGBoost模型的R2最大且MSE值最小，表明MC-XGBoost模型是所用模型中最优的预测模型。

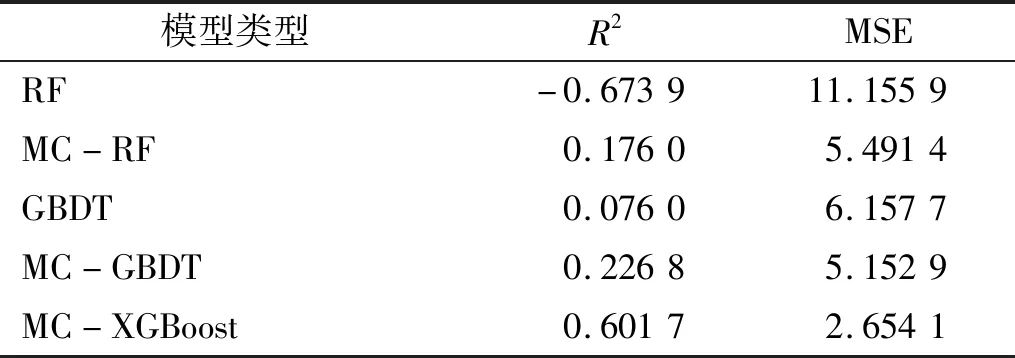
表5 不同模型误差对比Tab.5 Comparison of errors of different models

5 结 论

本文为探索某型航空发动机高压转子系统的装配参数与振动测试参数之间的内在关联特性，建立了一种MC-XGBoost的预测模型，并通过实测数据样本验证，得到如下结论：

(1)所提出的MC-XGBoost模型可用于航空发动机高压转子装配参数与整机试车振动响应参数关系模型的建立。将实测数据代入模型，结果表明，机匣上测点的振动响应对高压转子的几何偏心大小和HPT的不平衡量大小敏感。

(2)本文使用的MC系数可以用于数据样本间相关性的衡量，它与XGBoost模型相结合，可以克服XGBoost模型的过拟合问题，它与RF模型和GBDT模型结合，可以提高模型的预测精度，其中最优模型为本文提出的MC-XGBoost模型。

(3)实际航空发动机振动响应的影响因素繁杂，本文从高压转子的装配角度，给出了整机振动的关联模型，且预测结果显示高压转子装配的不平衡量和几何偏心对整机振动响应有较高的预测水平。