考虑土-结构相互作用的结构残余位移比谱

刘巴黎，胡进军，谢礼立

(1.中国地震局 工程力学研究所,哈尔滨 150080;2.中国地震局 地震工程与工程振动重点实验室,哈尔滨 150080)

1985年墨西哥米却肯州地震和1995年日本神户地震后，大量工程结构因残余位移过大而被拆除[1-2]。近二十年来，残余位移受到国内外学者[3-6]的关注并逐渐被运用于结构地震损失评估。文献[7]将残余位移作为决定结构是否可修复的重要指标。GB/T 38591—2020《建筑抗震韧性评价标准》[8]将结构残余层间变形作为韧性评价的重要指标，并给出了结构层残余位移角限值。

近年来国内外学者对残余位移进行了广泛的研究。Harikrishnan等[9]对单自由度(single degree of freedom，SDOF)体系残余位移比谱进行了系统研究，分析了场地类别、震级、断层距和持时对等延性残余位移比谱的影响，建立了SDOF体系等延性残余位移比谱。Saifullah等[10]针对双线性和捏缩滞回模型SDOF体系，研究了弹塑性特征参数及捏缩滞回模型参数对归一化残余位移谱的影响，构建了等延性残余位移谱的经验公式。张勤等[11]基于实际地震动记录，研究了SDOF体系模型和地震动不确定性对残余位移的影响，提出了残余位移的概率计算模型。黎璟等[12]提出了近断层脉冲型地震作用下结构残余位移设计谱。赵泰儀等[13]对比了RC桥墩静力滞回性能的试验以及模拟结果，分析了模拟不确定参数对RC桥墩残余位移建模方法的影响。王军文等[14]探索了RC桥墩残余位移与最大位移定量关系，分析了不同参数对RC桥墩残余位移的影响，建立了残余位移的回归方程。刘巴黎等[15]针对二维屈服面模型的单质点双自由度体系，提出了双向地震激励下的等强度残余位移谱模型。

由于地震波特性和场地土等因素的影响，地震激励下考虑SSI效应和基于刚性地基假定的结构响应存在差异。Veletsos[16]研究了SSI效应对弹性强度需求的影响，结果表明与基于刚性地基假定的结构相比，考虑SSI效应的结构周期延长，阻尼比增大而弹性强度需求减小。Ghannad等[17-18]分析了SSI效应对结构弹塑性特征参数的影响，研究表明考虑SSI效应与基于刚性地基假定的结构强度折减系数和延性系数存在较大差异。Eser等[19-20]研究了考虑SSI效应的SDOF体系弹塑性位移系数，认为考虑SSI效应与基于刚性地基假定的结构弹塑性位移系数存在明显差异，同时建立了考虑SSI效应的弹塑性位移系数回归方程。

目前针对残余位移的研究主要基于刚性地基假定，不能充分反映场地效应对结构残余位移的影响。一方面，考虑SSI效应后结构的弹性和弹塑性需求(强度和位移)与基于刚性地基假定的结构弹性和弹塑性需求存在明显的差别；另一方面，考虑SSI效应后结构周期延长和阻尼比增大使得基于刚性地基假定的残余位移响应值不够准确。

为了获得考虑SSI效应的结构残余位移谱，本文对考虑SSI效应的SDOF体系残余位移谱进行较为详细的研究，建立了考虑土-单自由度体系相互作用的模型，对比分析了SDOF体系基于刚性地基假定和考虑SSI效应的残余位移谱差异，分析了屈服强度系数η、高宽比h/r以及场地类别对残余位移均值谱和离散性的影响，给出了考虑SSI效应的残余位移谱预测方程，以期为精细化的抗震性能评估和抗震韧性评价提供参考。

1 考虑SSI效应的SDOF体系

1.1 单自由度体系运动方程

考虑SSI效应的SDOF体系模型，如图1所示。SDOF结构质量、质量惯性矩、刚度、阻尼系数和高度分别为m，I，k，c和h；基础假定为刚性圆盘，质量和质量惯性矩分别为mf和If，面积和有效半径分别为Af和r；土体可用弹簧和阻尼器来模拟，水平和转动方向刚度系数分别为kh和kφ、水平和转动方向阻尼系数分别为ch和cφ。刚度和阻尼系数的表达式为

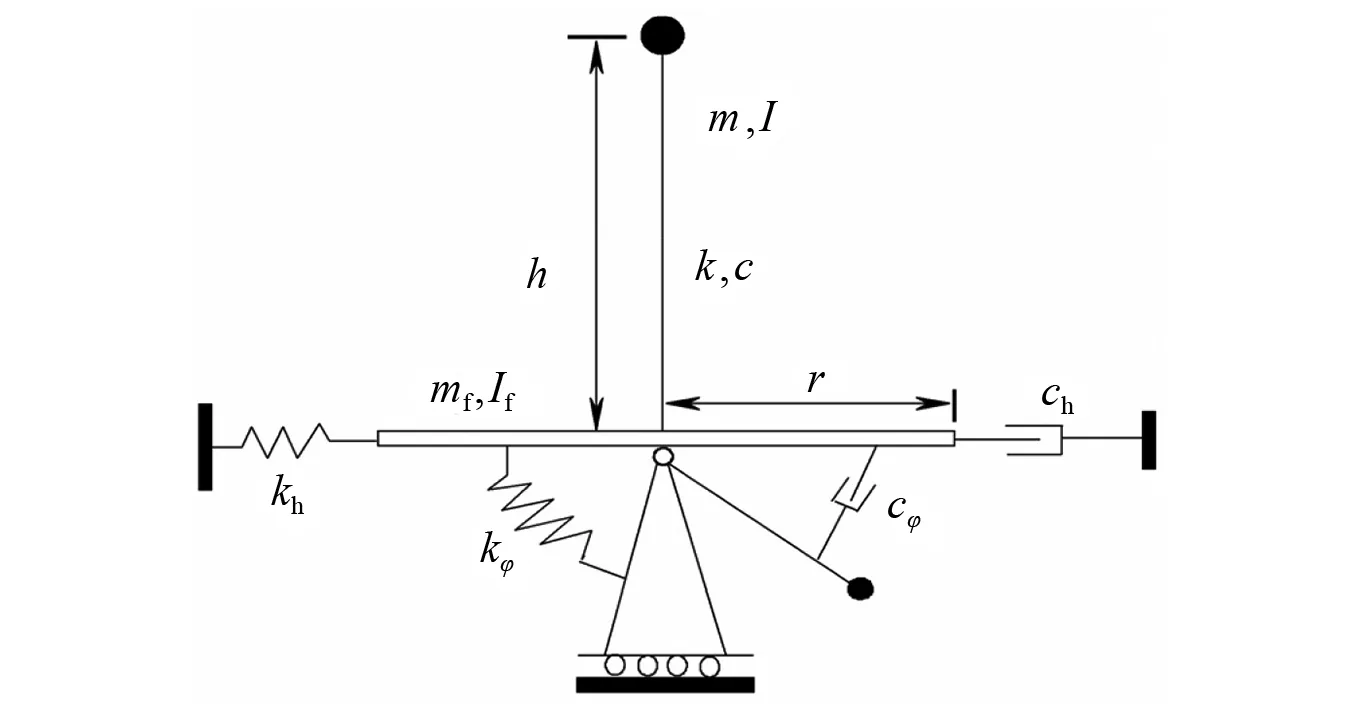
图1 土-单自由度体系相互作用简化模型Fig.1 Simplified model considering soil-SDOF system interaction

(1)

ch=ρVsπr2

(2)

(3)

cφ=ρVpπr4/4

(4)

其中:Vs为剪切波速；Vp为纵波波速；υ为泊松比；ρ为土体的质量密度。

针对图1所示的模型，建立考虑SSI效应的SDOF体系运动方程，如式(5)所示。计算模型由SDOF体系和允许由平动和转动的基础组成。基础-结构质量比mf/m取0.1，结构-土体质量比m/ρr2h取为0.5。

(5)

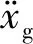
基于刚性地基假定的SDOF体系运动方程为

(6)

1.2 考虑SSI效应的简化计算方法

考虑SSI效应最常用的方法是将土体等效为具有刚度和阻尼的土弹簧。考虑SSI效应的SDOF体系的等效周期Teq和等效阻尼βeq[21]的计算公式为

(7)

(8)

式中：T为刚性地基假定对应的周期；β0为基础阻尼比，可由FEMA 450查图得到，如图2所示。

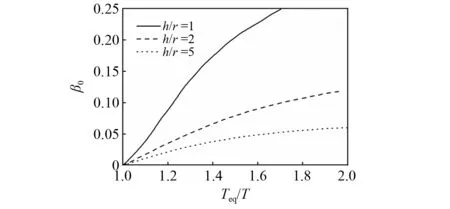
图2 基础阻尼比Fig.2 The foundation damping ratio

考虑SSI效应后结构的刚度变小，而屈服强度相对比较稳定[22]。考虑SSI效应的力-位移关系如图3所示。图3中:Fy和Fyeq分别为刚性地基和SSI效应的屈服强度;uy和uyeq分别为刚性地基和SSI效应的屈服位移。

图3 考虑SSI效应的力-位移关系Fig.3 Force-displacement relationships of the SSI system

1.3 残余位移比定义

研究结构残余位移ur时，通常采用不同的参数对ur进行归一化。常用的归一化参数包括：最大可能残余位移um,r、弹塑性谱位移sdi、弹性谱位移sde以及屈服位移uy。

屈服位移uy是最早被采用的归一化参数，Mahin等[23]针对理想弹塑性(elastic perfectly-plastic,EPP)模型SDOF体系，研究了屈服位移归一化后的等延性弹塑性谱。Farrow等[24]采用屈服位移对残余位移进行归一化。本文采用屈服位移uy对残余位移进行归一化，定义结构残余位移比(残余位移延性系数)Cr，计算公式为

(9)

1.4 模型参数取值

采用EPP的SDOF体系进行时程分析。屈服强度系数η分别取0.2，0.4，0.6，0.8和1.0，屈服强度系数的表达式如式(10)所示。

(10)

式中:PGA为地震动峰值加速度;ry为单位质量的屈服强度；自振周期T为0.1～3 s，周期间隔为0.1 s；结构高宽比h/r取1、2和5，土体参数如表1所示。

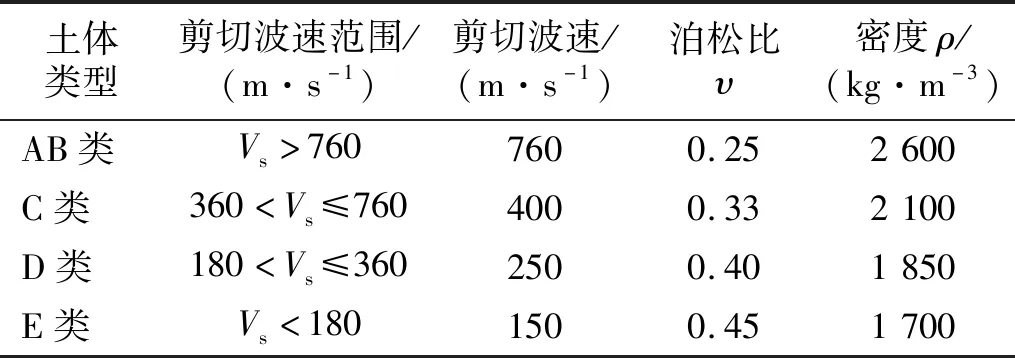
表1 土体参数Tab.1 Soil parameters

1.5 计算流程

本文编写了分析程序，建立基于刚性地基假定和考虑SSI效应的残余位移比谱。计算流程如图4所示。

图4 计算流程图Fig.4 Flow chart for calculating

步骤1地震波输入，积分步长采用文献[25]建议的方法，取地震动记录采样时间间隔，自振周期的1/25以及0.01 s三者的最小值。

步骤2基本参数输入，包括：质量、刚度、结构高度，基础宽度及土体参数；

步骤3计算等效周期和等效阻尼；

步骤4假定屈服强度系数，求取屈服位移；

步骤5时程分析，积分方法采用Newmark-β法，提取结构残余位移。

1.6 模型准确性验证

为了验证本文建立的模型准确性，对比了本文基于刚性地基假定得到的残余位移比谱与文献[26]中基于刚性地基假定的计算结果，如图5(a)所示。对比了本文基于刚性地基假定和考虑SSI效应得到的强度折减系数R谱与Ghannad等研究中对应R谱的计算结果，如图5(b)所示。强度折减系数R为地震作用下结构保持弹性所需的最小强度Fe与屈服强度Fy之比，计算公式如下式所示。图5(a)横坐标为结构周期T，纵坐标为残余位移比Cr；图5(b)横坐标为结构周期T，纵坐标为强度折减系数R和屈服强度系数η的乘积。由图5可知，本文的统计结果和Ghannad等和Ruiz-Garcia等研究中的统计结果在整个周期段内差距较小，确保了本文建立的考虑SSI效应SDOF模型的准确性。

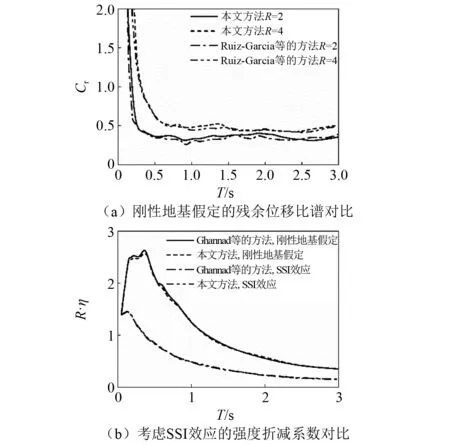
图5 本文结果与已有文献结果的对比Fig.5 Comparison between the results of this study and those of existing literatures

(11)

2 地震动记录选取

本文基于美国太平洋地震工程研究中心(PEER NGA-West2)强震数据库，选取了1952年—2011年全球范围内18次地震事件的280条地震记录，挑选原则[27]如下：①矩震级Mw>5.7，排除对结构造成损伤较小的地震；②地震动峰值加速度(peak ground acceleration,PGA)大于40 cm/s2；③仪器位于自由场地；④不包含脉冲型地震动。将选取的地震记录依照据NEHRP规范的场地划分标准分为四类，AB类(A类和B类合为一类)、C类、D类及E类，每类场地各选取了70条地震记录。地震动的震级-断层距分布如图6所示。

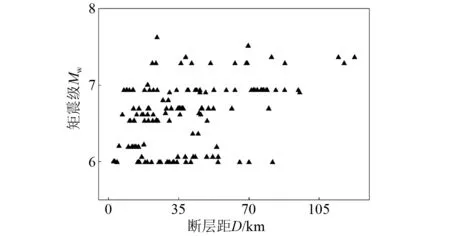
图6 震级-断层距分布图Fig.6 Magnitude-fault distance distribution of strong ground motion data

3 分析结果

3.1 屈服强度系数η的影响

屈服强度系数反映了结构屈服强度相对地震作用大小的程度[28]。分别取屈服强度系数η=0.2,η=0.4,η=0.6,η=0.8以及η=1.0，计算得到的残余位移比均值谱如图7所示。可以看出：基于刚性地基假定和考虑SSI效应的残余位移比谱值随屈服强度系数η增大而减小；屈服强度系数η对残余位移比谱的影响与周期T相关。残余位移比谱随周期增大逐渐减小；不同屈服强度系数η对应残余位移比谱的差距随周期增大而减小。总体而言，T>1.0 s时，基于刚性地基假定和考虑SSI效应下不同屈服强度系数η对应的残余位移比谱差距较小。由于篇幅有限，本文只给出了AB类和E类场地下基于刚性地基假定和考虑SSI效应的残余位移比谱，C类和D类基于刚性地基假定和考虑SSI效应的残余位移比谱与AB类和E类场地的结论类似。

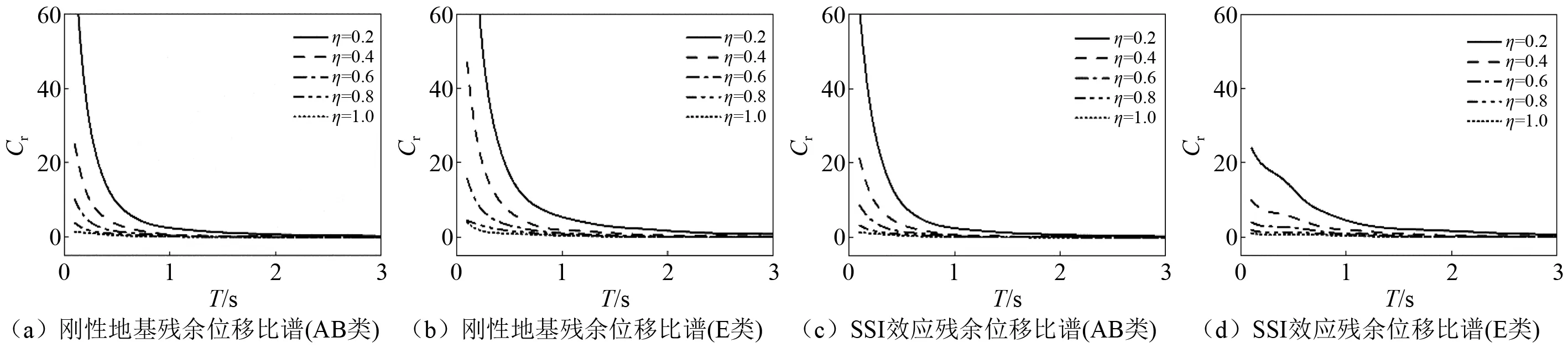
图7 屈服强度系数η对残余位移比谱的影响Fig.7 Influence of yielding strength factor on residual displacement ratio spectra

3.2 高宽比h/r的影响

高宽比h/r为结构高度和基础半径之比，反映了SSI效应的程度。分别取高宽比h/r为1、2和5，计算得到的残余位移比均值谱如图8所示。可以看出：高宽比h/r对残余位移比谱的影响与场地类别及周期T有关。存在临界周期点，当周期小于临界值时基于刚性地基假定的残余位移比谱值大于考虑SSI效应的残余位移比谱谱值；当周期大于此临界值时，基于刚性地基假定和考虑SSI效应的残余位移比谱值差距很小。AB类和C类场地对应的临界周期为0.5 s，D类场地对应的临界周期为0.8 s，而E类场地对应的临界周期则为1.2 s。当周期小于临界值时，残余位移比谱值随高宽比h/r的增大而减小，说明SSI效应程度越大，残余位移比谱越小。

3.3 数据显示 为测试昆虫生境移动监测软件的数据显示功能模块能否正常运行，本节通过自定义的两个String类型的数组title〔〕和text〔〕分别模拟生境因子名称以及对应的参数值，内容如下：

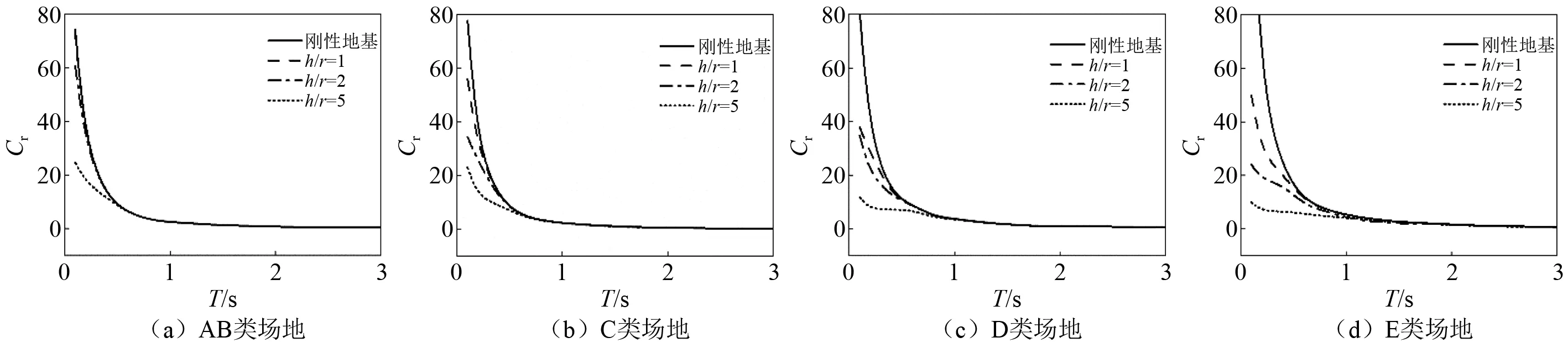
图8 高宽比h/r对残余位移比谱的影响Fig.8 Influence of aspect ratio on residual displacement ratios spectra

3.3 场地条件的影响

基于刚性地基假定和考虑SSI效应的残余位移比均值谱分别为Cr,fix和Cr,SSI，分别采用场地类别AB类、C类、D类及E四类的刚性地基假定的残余位移比对考虑SSI效应的残余位移比进行标准化，得到标准化的残余位移比谱Cr,SSI/Cr,fix，如图9所示。可以看出：场地类别对标准化的残余位移比谱有一定影响，场地类别对标准化的残余位移比谱的影响与周期T有关，场地土越软则标准化的残余位移比谱值越小。不考虑SSI效应的影响会高估结构残余位移比，高估值随场地土变软而增大，说明基于刚性地基假定的残余位移计算结果偏于安全。

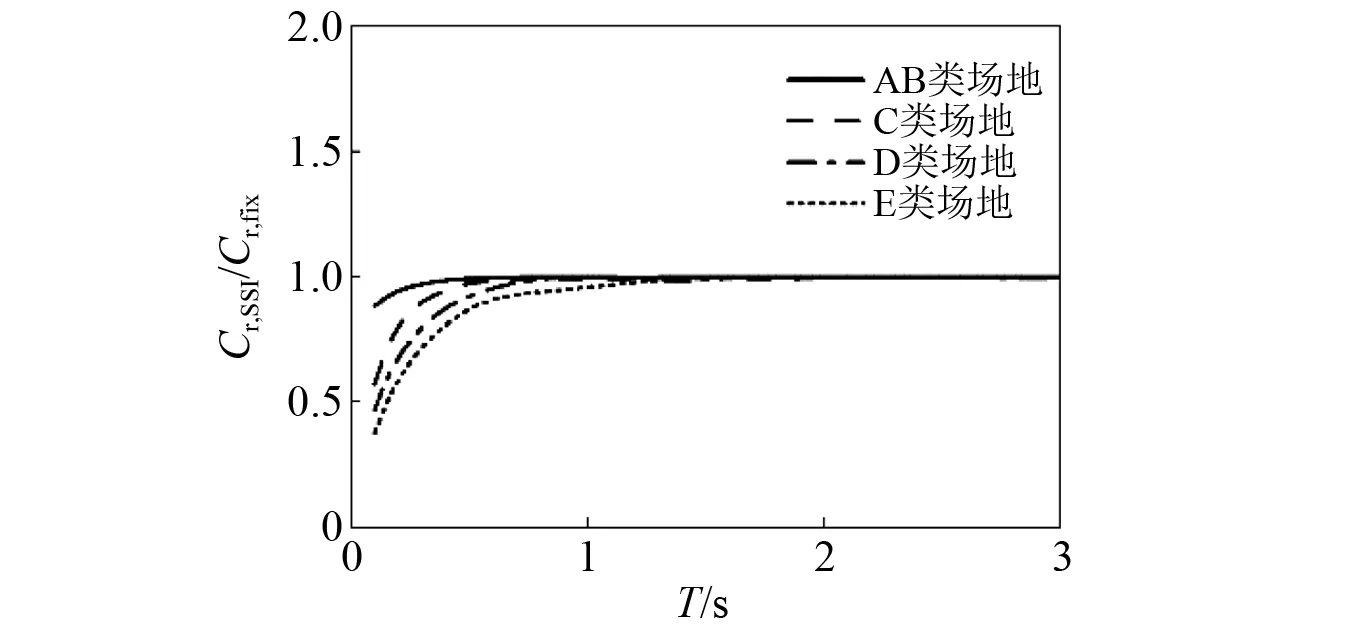
图9 场地类别对残余位移比谱的影响Fig.9 Influence of site condition on residual displacement ratio spectra

4 残余位移比离散性分析

采用变异系数(样本标准差与均值之比)来描述残余位移比的离散性，研究场地类别、屈服强度系数和高宽比对残余位移比离散性的影响，图10给出了不同条件下残余位移比离散性谱。可以看出：场地类别和屈服强度系数对残余位移比变异系数有一定影响，高宽比h/r对残余位移比变异系数的影响较小。周期小于0.8 s时，残余位移比的变异系数随周期增大而减小；周期大于0.8 s时变异系数趋于不变，即周期大于0.8 s时残余位移比变异系数对周期变化不敏感。

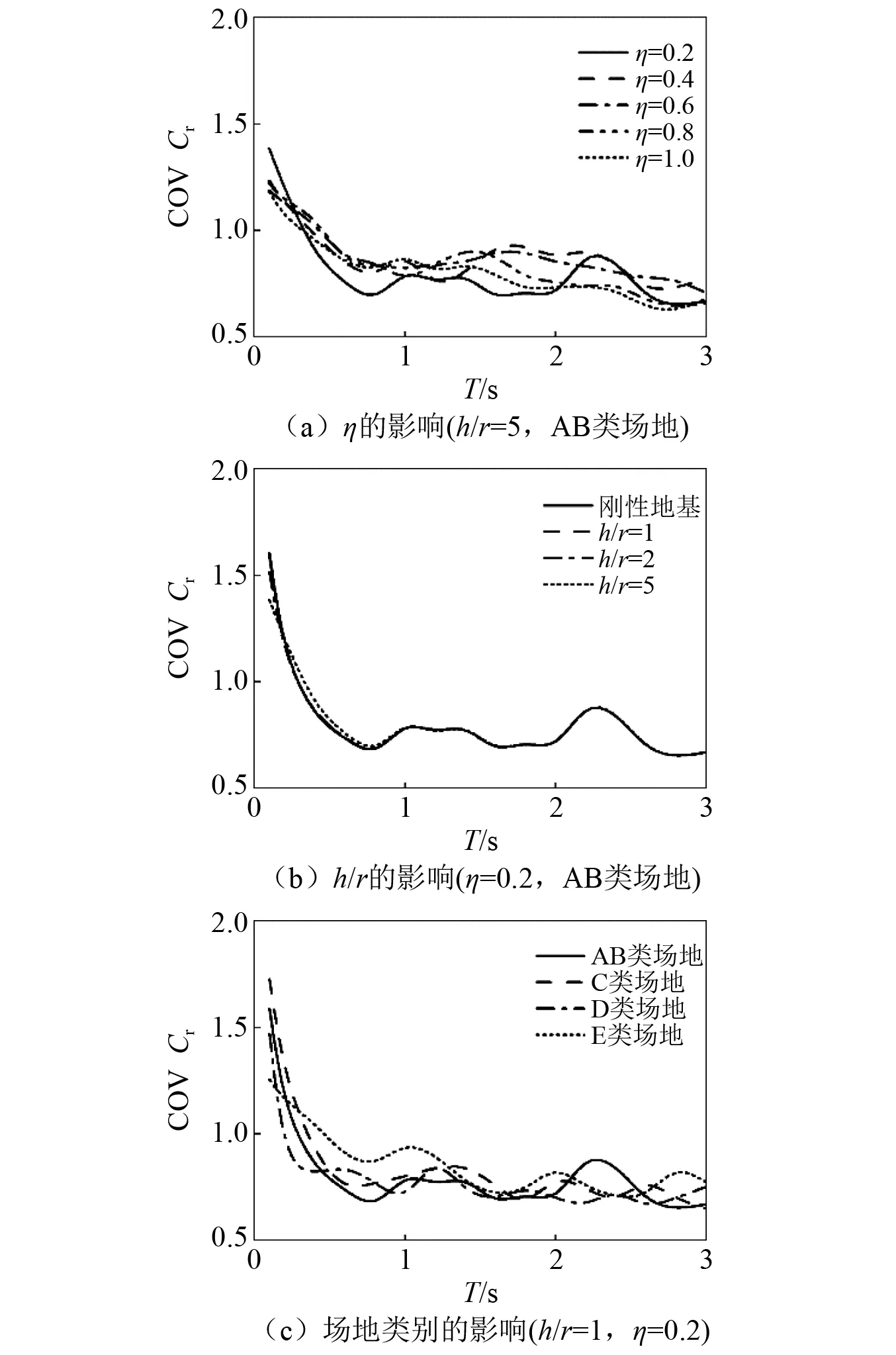
图10 残余位移比变异系数谱Fig.10 COVs of residual displacement ratios

5 回归分析

采用变异系数(样本标准差与均值之比)来描述根据前文所述，屈服强度系数η、高宽比h/r以及场地类别对残余位移比谱影响显著，对残余位移比谱进行回归分析时也必须考虑这些因素的影响。由图7可以看出各曲线具有较为统一的谱形，考虑SSI效应的残余位移比谱预测方程如式(12)所示。

Cr,SSI=a·ηb·T0.8[1-0.4·exp(c·ηd)]

(12)

考虑SSI效应残余位移比谱的回归参数a，b，c和d可通过非线性最小二乘Levenberg-Marquardt算法回归分析[29]得到，回归参数值如表2所示。高宽比h/r是结构周期比Teq/T的重要影响因素，本文建立的残余位移比拟合公式没有将高宽比h/r作为函数的自变量，而在回归参数中考虑高宽比h/r的影响。根据预测方程得到的残余位移比计算值和实际值如图11所示。由于篇幅有限，本文只给出了不同场地类别下当η=0.6和η=1.0时考虑SSI效应残余位移比计算值和实际值的对比。可以看出本文建立的残余位移比谱预测方程能较为精确的评估考虑SSI效应的结构残余位移。

表2 式(12)中的回归参数Tab.2 Regression parameters in equation(12)

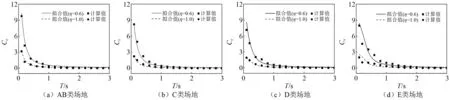
图11 考虑SSI效应的残余位移比统计值和预测值对比Fig.11 Comparisons between statistical results and prediction results of residual displacement ratios considering SSI

6 结 论

针对考虑SSI效应的SDOF结构模型，分析了屈服强度系数η、高宽比h/r及场地类别对结构残余位移比谱和离散性的影响，建立了基于刚性地基假定和考虑SSI效应的结构残余位移比谱预测方程。主要结论如下：

(1)存在临界周期点，当周期小于临界值时考虑SSI效应的残余位移比谱谱值小于基于刚性地基假定的结构残余位移比谱值，且残余位移比谱值随着高宽比h/r的增大而减小；当周期大于临界值时，考虑SSI效应和基于刚性地基假定的结构残余位移比谱差距很小；AB类、C类、D类和E类场地的临界周期分别为0.5 s,0.5 s,0.8 s和1.2 s。

(2)不考虑SSI效应的影响会高估结构残余位移比值，高估的程度随场地土变软而提高，而基于刚性地基假定得到的结构残余位移计算偏于保守。

(3)考虑SSI效应的结构残余位移比均值谱随屈服强度系数η增大而减小；场地类别和屈服强度系数η对考虑SSI效应的结构残余位移比离散性有一定影响，高宽比h/r对考虑SSI效应的结构残余位移比离散性影响较小。

(4)建立了考虑SSI效应的结构残余位移比谱预测方程，结果可为精细化的抗震性能评估和抗震韧性评价提供参考。

致 谢

感谢美国太平洋地震工程研究中心(PEER)NGA计划项目提供的地震动数据！