基于声成像与卷积神经网络的轴承故障诊断方法及其可解释性研究

王 冉，石如玉，胡升涵，鲁文波，胡 雄

(1.上海海事大学 物流工程学院，上海 201306；2.北京海基嘉盛科技有限公司 上海分公司，上海 201100)

滚动轴承作为机械系统的重要零件，广泛应用于风机、发动机等设备[1]。据统计，旋转机械的故障中由于轴承损坏导致的故障约占30%。因此，对滚动轴承进行及时的故障诊断至关重要。

目前滚动轴承的故障诊断主要是基于振动信号的测量和分析。振动信号由振动传感器采集后，对其通过一系列信号处理方法[2-4]进行故障特征提取。最后采用机器学习方法对提取的特征进行分类[5]。由于实际应用中振动信号的测量通常需要以接触的方式进行。在某些恶劣的测试环境情况下，很难在机器表面安装加速度计等振动传感器。因此，发展基于非接触式测量的故障诊断方法是非常必要的。

声信号是设备振动在空气中传播产生的，同样包含了丰富的机器健康状态信息，且可以通过非接触式传声器获取。目前声学故障诊断(acoustics-based diagnosis,ABD)已经得到了一定的应用。Ao等[6]利用麦克风采集列车轴承声学信号进行列车轴承路旁故障诊断。Li等[7]采用声学和振动信号数据融合的方法进行齿轮箱故障诊断。然而，上述方法中，声信号是由单个或少数几个传声器测量，然后采用和振动信号处理相似的方法进行处理。单个测点的声信号容易受到反射波、散射波和其他声源辐射噪声的干扰和污染，抗干扰能力差。同时，上述方法对测点位置敏感，难以对机器的缺陷部件进行定位，只能用于简单设备的初步异常判断。

随着声成像技术和低成本MEMS传声器阵列技术的发展，一些研究者尝试将近场声全息(near-field acoustic holography,NAH)和远场波束形成等声学成像技术应用于机械故障诊断。鲁文波等[8]提出一种基于近场声全息和灰度共生矩阵(gray-level co-occurrence matrix,GLCM)的齿轮箱故障诊断方法。Wang等[9]提出一种基于声像图和Gabor小波变换(Gabor wavelet transform，GWT)的轴承故障诊断方法。这些方法中的特征是人为设计提取的，提取这些特征需要大量的先验知识。

深度学习方法可以自动学习并处理大规模数据，已被引入到机械智能故障诊断中。Yao等[10]提出了一种基于声信号和卷积神经网络的齿轮故障诊断方法。Kumar等[11]提出了一种改进的深度卷积神经网络模型，将声信号进行小波变换得到的声像图来识别离心泵的缺陷。上述的基于深度学习的故障诊断方法均没有提供模型决策结果的可解释性说明，缺乏工程上的物理解释。深度学习的可解释性探讨在图像领域研究较为丰富。文献[12]通过类激活图(class activation map,CAM)使得卷积神经网络有了定位能力。在CAM基础上，文献[13]提出了使用范围更广的梯度加权类激活图(gradient-weighted class activation map，Grad-CAM)方法对模型学习的重点关注区域进行可视化。目前基于深度学习的机械故障诊断方法虽然已经取得了较高的识别精度，但对智能故障诊断决策结果的可解释性说明研究较少。张俊鹏等[14]对卷积神经网络在轴承故障诊断中的可解释性进行了探究，为卷积神经网络在故障诊断领域的工程应用提供参考。

针对上述故障诊断方法中存在的不足，本文提出一种基于声成像与卷积神经网络的滚动轴承声学故障诊断方法。首先使用波叠加法将传声器阵列获取滚动轴承辐射声场进行声成像，然后将声像输入卷积神经网络进行故障分类。为了对模型分类结果进行可解释性说明，本文采用基于梯度加权的类激活图[15]突出声像图中的重要区域，寻找模型重点关注区域与目标类别之间的联系，为模型的学习结果提供可解释性说明。

1 波叠加法原理

波叠加法(wave superposition method，WSM)可以精确地重建任意形状声源的声辐射，且复杂度低、易于实现。基于波叠加法的声场重建示意图如图1所示。将具有边界S的任意形状振动体浸入密度为ρ、声速为c的无界均匀流体介质中，声源面S的外部区域表示为E。假定等效的简单辐射源(单极子)连续分布在声源面S内部的虚拟面SV上。任意场点P和虚拟源Q的位置矢量分别表示为r和ro。O表示坐标系的原点。由传声器阵列构成的测量面H和重建面R均平行于x-y平面。

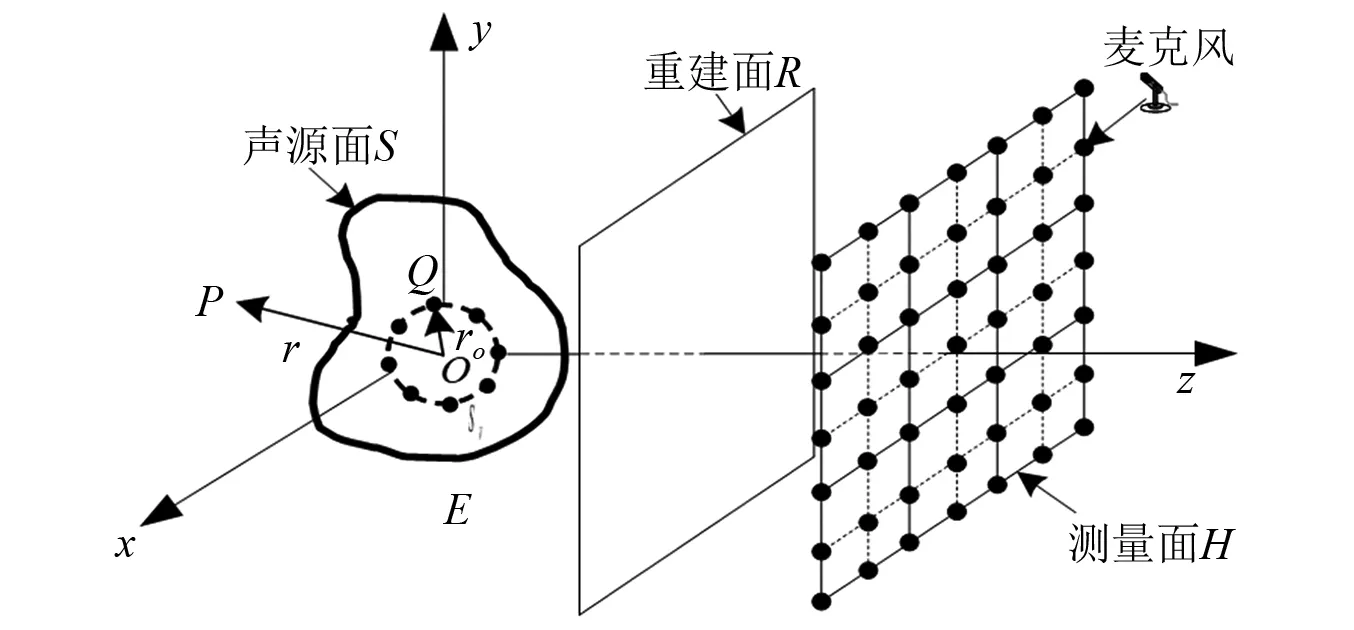
图1 基于波叠加法的声场重建示意图Fig.1 Schematic diagram of sound field reconstruction based on wave superposition method

根据波叠加法[16]理论，任意形状声源的声场可以用分布在虚拟表面SV上的一系列虚拟声源等效地代替。因此，外部区域E的声压可以写成

(1)

式中：ω为角频率;q(r0)为声源强度;G为自由空间格林函数，其定义为

(2)

在实际应用中，为了简单起见，等效声源通常均匀分布在规则的虚拟曲面SV上，将SV离散为M个元素，并且假设每个元素的声源强度q(r0)为常数，k=ω/c是波数。如果传声器阵列中的测量点数量为N，测量点的声压PH可以用矩阵形式表示为

PH=iωρGHVq

(3)

式中:PH=[p(r1),p(r2)，…，p(rN)]T;q为等效源强;GHV为等效声源强度与测量点声压相关联的传递矩阵，其元素可根据式(2)计算。给定测量声压PH，可以通过将相应的矩阵GHV取广义逆矩阵来计算q。

(4)

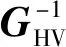
最后，重构面R上各场点的声压PR可重构为

PR=iωρGRVq

(5)

式中，GRV为重建点与虚源点的声场传递矩阵，可通过将重建点的位置代入式(2)求出。随后，重建面的重构声压可以表示为二维声像。

2 基于声成像与CNN的滚动轴承故障诊断方法

本文所提方法流程图如图2所示，整体上可以划分为离线训练和故障诊断两个阶段。具体步骤如下：①声信号获取，采用传声器阵列获取滚动轴承在不同运行状态下的声信号；②使用波叠加法对采集的声信号进行声成像，选择外圈故障频率、内圈故障频率、滚动体故障频率作为重建频率；③将通过波叠加法获取的轴承不同状态下的声像图划分为训练集和测试集两部分，训练集用来训练卷积神经网络模型；④使用训练好的卷积神经网络对测试集声像图进行故障诊断。

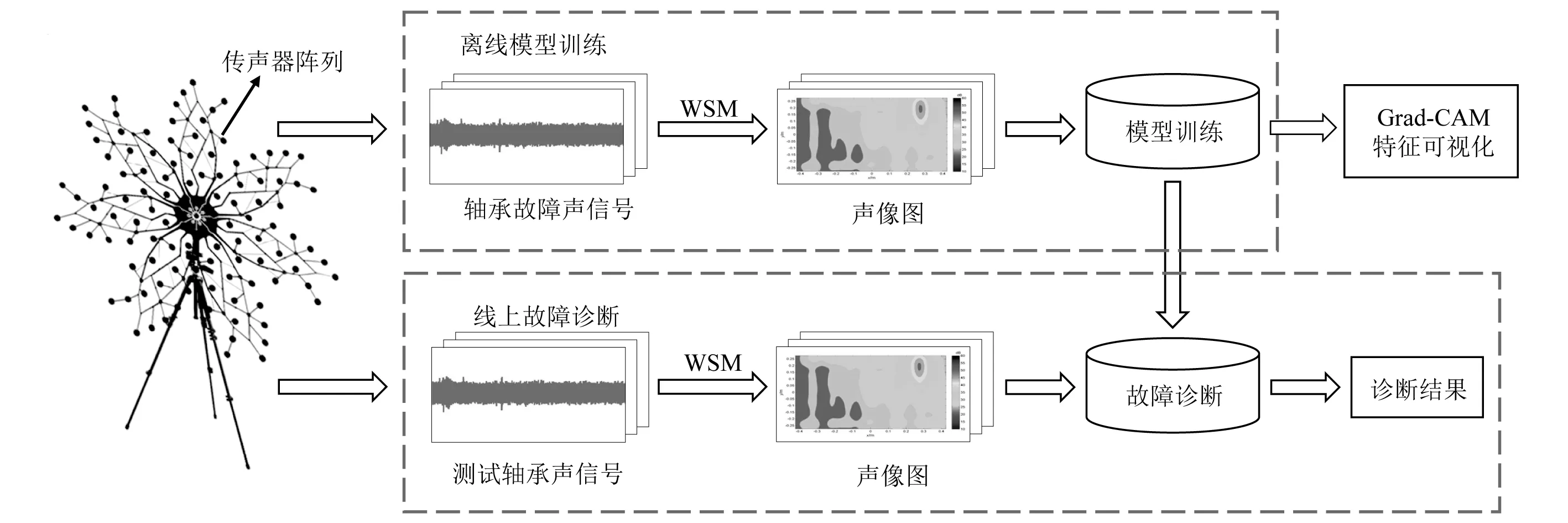
图2 基于声成像和卷积神经网络的滚动轴承声学故障诊断方法流程图Fig.2 Flow chart of acoustic fault diagnosis method of rolling bearing based on acoustic imaging and convolutional neural network

在完成模型训练之后，为了验证模型分类结果的可信度，本文采用梯度加权的类激活图算法对模型重点关注区域与目标类别之间的联系进行可视化，将声像图中对网络决策结果的贡献程度以类激活图的形式进行展示。基于WSM的声成像技术已在第1章进行了介绍，接下来分别对基于CNN模型的声像故障诊断过程及基于Grad-CAM的特征可视化方法进行介绍。

2.1 基于卷积神经网络的轴承故障诊断

本文方法中使用的卷积神经网络借鉴了常用的LeNet-5模型，并在其基础上做了如下两点改进：①在每个卷积层后面都先进行批归一化处理再使用激活函数，有利于加快模型的训练速度，提高模型的泛化能力；②使用全局平均池化层(global average pool,GAP)代替全连接层，减少模型的参数量，有助于减小网络训练的时间，且使网络不易出现过拟合。改进后的卷积神经网络结构示意图如图3所示，包括卷积层、池化层、全局平均池化层三类。

(1)卷积层。卷积层是卷积神经网络的核心构建块。本方法中，模型的输入是不同运行状态下轴承的二维空间声像，输出特征计算如式(6)所示

(6)

(2)池化层。卷积层之后利用池化层来对特征图进行降维处理，本文采用最大池化，计算公式为

(7)

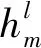
(3)全局平均池化层。全局平均池化是对最后一层池化后的特征图进行全局求平均值。网络输出的标签是不同类型的轴承故障声像图各自对应的标签。

各层神经网络的详细参数如表1所示。

表1 卷积神经网络的详细参数Tab.1 The detailed parameters of convolutional neural network

2.2 基于梯度加权类激活图的特征可视化

基于梯度加权类激活图的特征可视化方法可以对神经网络的分类结果作出合理的解释。该方法结合神经网络输出的特征图来计算类激活图，如图3所示，建立特征与目标类别相关的二维分数网格。每个网格所对应的分数都代表该位置对分类结果的重要程度，分数越高的地方代表模型越加关注该区域。其计算过程如下：

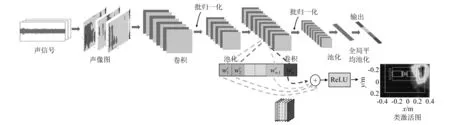
图3 卷积神经网络结构及基于Grad-CAM的特征可视化过程Fig.3 Structure of the proposed convolutional neural network and feature visulization process using Grad-CAM

(1)获得训练后的CNN模型对应任意类别c的类激活图。第k个特征图对应类别c的权重为

(8)

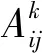
(2)求得所有特征图对应目标类别的权重后，将权重与对应的特征图进行加权求和。并且将Relu函数应用于特征图的线性组合

(9)

3 试验验证

3.1 数据集介绍

为了验证所提方法的有效性，在上海交通大学机械系统与振动国家重点实验室的半消声室中进行了滚动轴承故障诊断试验。试验装置如图4所示。试验台由一台机组、试验轴承、传声器阵列、三个参考传声器(标号1、2、3)和数据采集系统组成。传声器阵列由12个具有均匀5 cm间距的传声器组成。测量面高出轴承试验台上表面5 cm。测量面与试验轴承之间的距离约为10 cm。采用线型传声器阵列在测量面上逐步扫描的方法进行声信号的采集。线阵搭载在一台异步电机上进行自动扫描，异步电机扫描步距为5 cm，步数为18步，最终获得一个85 cm×55 cm的测量网格。

图4 试验平台Fig.4 Experiment platform

试验轴承的类型是GB6203型滚动轴承，其结构参数如表2所示。本文研究了三种典型的轴承故障类型，包括外圈故障(outer race fault，ORF)、内圈故障(inner race fault,IRF)和滚动体故障(rolling ball fault，RBF)。为了模拟不同的故障严重程度，采用电火花加工技术对轴承内圈、外圈、滚动体的局部点蚀缺陷进行了处理。对于ORF和IRF有S、M、L三种不同的损伤尺寸，分别为3.5 mm×0.5 mm×0.5 mm，3.5 mm×1.0 mm×0.5 mm，3.5 mm×1.5 mm×0.5 mm。RBF损伤尺寸为3.5 mm×0.5 mm×0.5 mm。综上所述，本文主要研究了8种故障类型，包括7种故障类型和一种正常状态(normal condition,NC)。图5展示了内圈、外圈两种故障下的试验轴承。

表2 GB6203滚动轴承参数Tab.2 Parameters of GB6203 rolling bearing

图5 试验轴承Fig.5 Experimental bearings

数据采集系统记录了8种故障类型下滚动轴承的声信号。数据采样频率为4 096 Hz。对于每种故障类型，在5种不同的载荷下收集声信号，共获得40个记录。每个载荷下每种故障类型有45个样本，每个样本的数据长度为16 384个点。

3.2 WSM声成像获取轴承声像样本

将数据集中的每一个样本，利用波叠加法通过声场重建获得不同运行状态轴承的声像样本。选择轴承试验台上表面距离测量面5 cm处作为重建面，将重建面划分为18×12个重建点的矩形网格。18×12个虚拟单极子作为等效源均匀地排列在在重建面下方0.05 m处的虚拟平面上。

试验中，轴的旋转频率fr约为12 Hz。ORF、IRF和RBF的故障特征频率分别为fo=36.6 Hz，fb=47.8 Hz，fi=59.4 Hz。由于机械系统的声信号是由振动引起的，因此，在声学成像中选择这三个故障特征频率作为WSM中的重建频率。图5展示了不同轴承故障类型下三个故障特征频率重建的部分声像图。

在图6中，为了更直观地展示声源定位结果，从俯视图来看，将重建的声像图与轴承试验台示意图(白线)重叠，其中颜色的深浅代表了声压级的高低，颜色越浅代表声压级越高，反之颜色越深代表声压级越低。可以看出，声像图中的热点几乎都在(0.275 m，0.125 m)位置，与试验轴承的位置一致。此外，坐标(0.275 m，0.225 m)周围的声压级也很高。这主要是因为辐射的声波和反射的声波在这个区域是重叠的。这些重建的声像图可以帮助定位和识别主要的噪声源，直观地反映辐射声场的空间分布。

图6 在不同轴承故障类型下以三个特征频率重建的声像图Fig.6 Acoustic image reconstructed with three characteristic frequencies under different bearing fault types

3.3 轴承故障诊断试验结果分析

在训练阶段，整个数据集有1 800个样本共包含8种故障类型。从中随机抽取1 500个样本作为训练集，同时保证每种故障类型的样本数量相同。剩下的300个样本作为测试集。选取交叉熵作为损失函数，Adam算法作为优化器。其学习率为3×10-4，epoch的总数设置为400，批量大小为150个，为了防止过拟合，这里在每层卷积后添加dropout，并设置其值为0.3。

在测试阶段，为了避免偶然误差，我们选取了10次试验结果的分类精度如表3所示。可以看出所提出的方法在10次试验中均取得了良好的诊断效果。最大准确度为99.33%，最低准确度为98.33%，平均准确度为99 %。

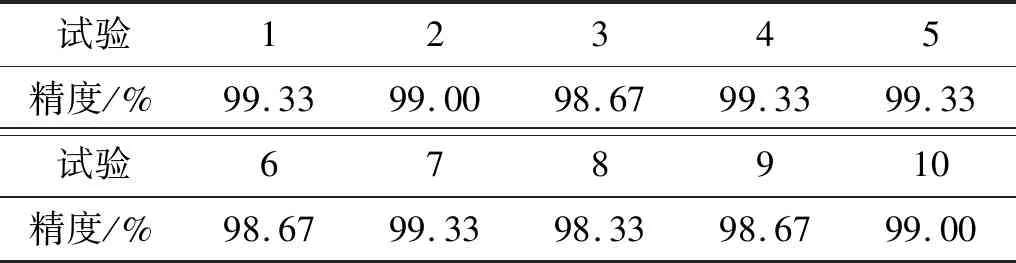
表3 卷积神经网络模型的10次试验测试集精度Tab.3 The accuracy of the 10 experiments test set of the improved convolutional neural network model

为了详细显示每种故障类型的诊断结果，取10次随机试验中某一次试验结果进行展示，测试集精度的混淆矩阵如图7所示。可以看出，除了故障类型2(IRF-S)和故障类型4(IRF-M)中有少量样本分类错误之外，其他测试样本均取得100%的分类精度，说明模型具有较高的分类精度。

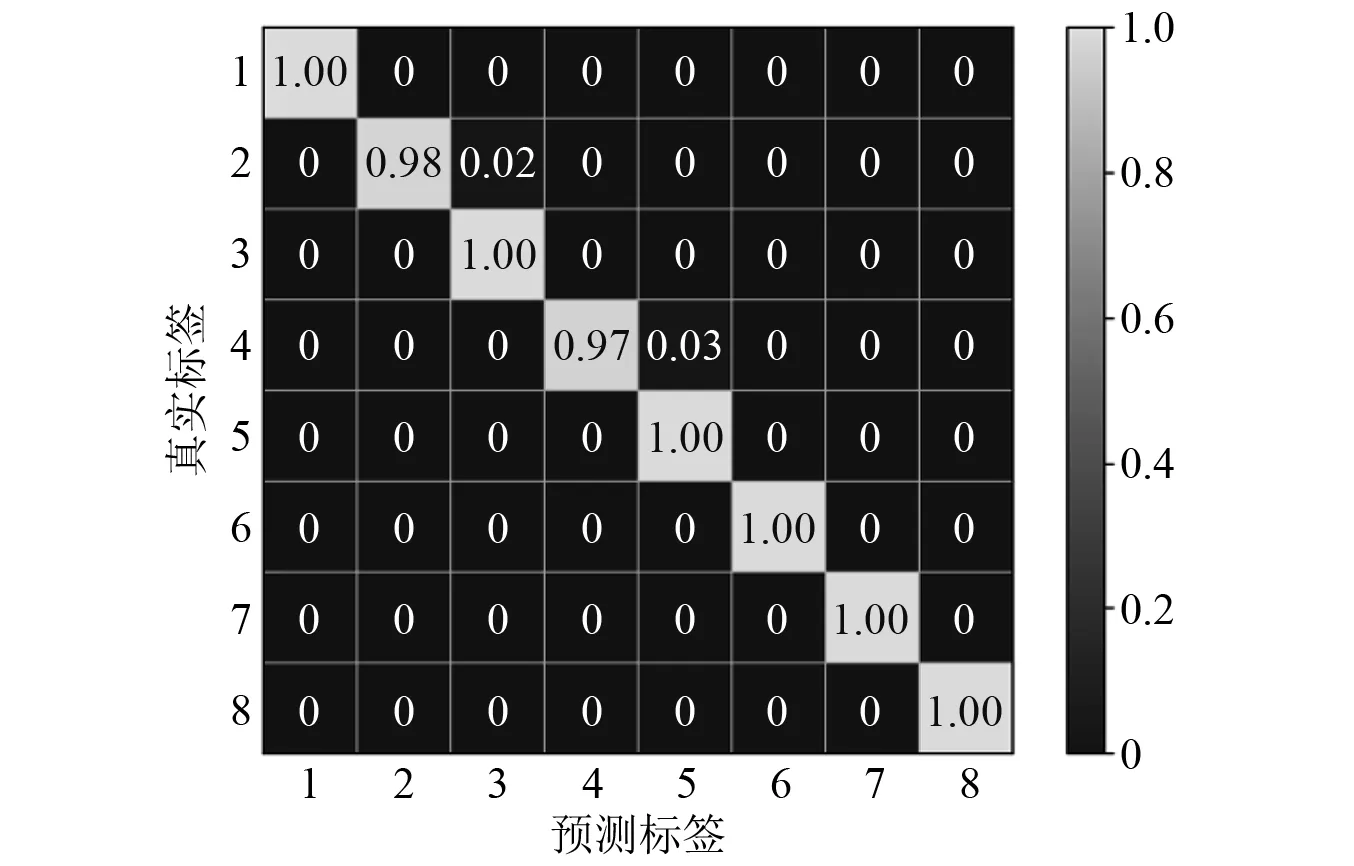
图7 试验1分类结果的混淆矩阵Fig.7 Confusion matrix of the classification results of the first experiment

为了进一步验证基于声成像与卷积神经网络的轴承故障诊断方法的抗干扰能力，在滚动轴承声场重建得到的声像图中加入一定的随机噪声，然后对加噪后的声像图进行故障诊断。当SNR=10 dB时，滚动轴承4种状态下在36.6 Hz处的重建声像如图8所示。

从图8中可以看出，受随机噪声的影响，轴承声像局部像素点处的声压级大小发生了变化，导致声像的纹理细节产生了无规则的变化，但是声像整体反映的声场空间分布特征基本保持不变，仍然可以从中挖掘出轴承不同状态下的声场分布规律。

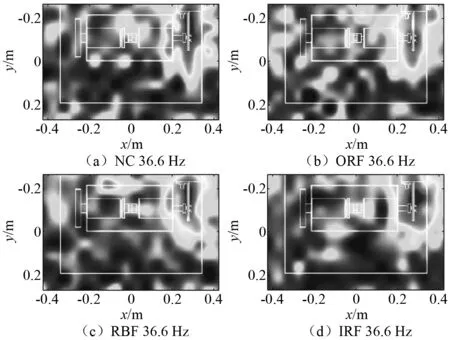
图8 SNR=10 dB时滚动轴承不同状态下的声像Fig.8 Acoustic images with SNR=10 dB of bearings in different operating conditions

对加噪后的声像图进行故障诊断，同样的，为了避免偶然误差，选取10次试验结果的分类精度如表4所示。可以看出所提出的方法在10次试验中均取得了良好的诊断效果。诊断准确率最大为95.66%，最低为92.98%，平均准确率为94.13 %。上述结果说明基于声像的故障诊断方法具有较强的鲁棒性。

表4 SNR=10 dB时10次试验测试集精度Tab.4 The accuracy of the 10 experiments test set of the SNR=10 dB

3.4 方法对比

为了验证所提方法相比现有的基于声像特征提取的声学故障诊断方法的优越性，这里与以下两种常用的方法进行分类精度对比。在利用波叠加法将声信号获取声像图之后，方法1从重建的声像图中提取基于灰度共生矩阵的4个方向(0°，45°，90°和135°)的纹理特征；方法2从重建的声像图中采用Gabor小波变换提取特征。最后都使用支持向量机对两种方法所提取特征进行分类。为了方便，下文记两种方法为WSM+GLCM+SVM和WSM+GWT+SVM。

两种方法的分类结果如图9所示。根据对比可知，本文所提出的方法平均诊断准确率(99.13%)高于WSM + GWT + SVM和WSM + GLCM + SVM。且能消除人工特征提取的不便。同时WSM + GWT + SVM方法的分类精度要远远高于WSM + GLCM + SVM方法，这意味着声像的GLCM特征对于轴承故障诊断来说是无效的，而通过GWT获得的Gabor特征更有效。以上比较表明，尽管基于声成像和声像特征提取的方法可以克服测量位置选择的困难并实现声源识别，但是它们的诊断结果仍然严重依赖于选择的声像特征提取方法。

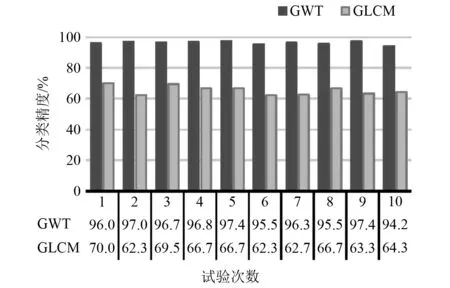
图9 基于两种声像特征提取的ABD方法的分类精度Fig.9 Classification accuracy of ABD method based on two types of acoustic image feature extraction

3.5 分类结果的可解释性

上述试验结果及对比分析验证了本文所设计的CNN模型能够自适应地从不同状态的轴承声像中学习到不同故障的特征，进而辨别不同的故障类型，具有较高的诊断精度。然而，和目前常用的基于深度学习的故障诊断方法一样，CNN模型类似一个“黑盒子”，分类结果缺乏可解释性。本文通过Grad-CAM算法，对用于轴承声像故障诊断中CNN模型的分类结果进行可解释性分析。图10显示了不同轴承故障类型的声像图经过Grad-CAM算法后获得的类激活图。类激活图使用渐变的色调显示，颜色越深代表模型在此处的激活程度越大，也就是说该区域对最终分类的影响越大。与图6表示的声像图不同，类激活图中的热点表现的是模型对声像样本的关注度。图中白线是轴承试验台的俯视图。

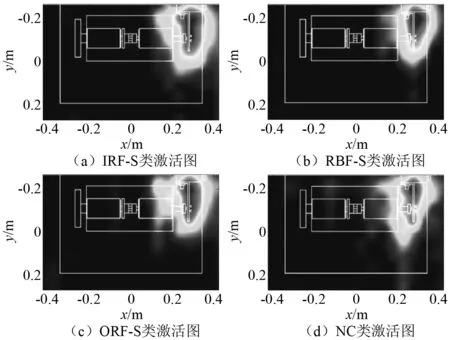
图10 轴承不同故障和正常状态声像图的类激活图Fig.10 Class activation diagrams of different fault and normal state sound images of bearings

从图10中可以看出，类激活图颜色较深的部分都在坐标(0.275 m，0.125 m)附近，也就是在试验台上轴承位置附近，说明对模型分类结果贡献最大的部分来自轴承。对于3种不同类型的故障以及正常状态下的轴承声像图，声像样本训练得到的CNN诊断模型对输入样本激活程度较大的部分均集中在声源附近，该部分的信息对于网络的分类结果具有较高的权重，说明网络识别该类别重点关注区域在声源附近。上述结果和实际情况一致，在本试验中，主要声源位置即轴承附近的声场分布中含有较多的故障特征信息，表明训练得到的CNN模型关注到了声源附近的声场分布。此外，如图10(d)所示，正常状态下的类激活图中权重分布较为分散，这也和实际中轴承正常状态下声场能量分布较为分散的情况一致。综合上述分析结果可以得出结论：本方法的分类结果具有较高的可信度。

4 结 论

本文针对现有的轴承声学故障诊断方法的不足，提出了一种基于声成像与卷积神经网络的滚动轴承声学故障诊断方法，并对其可解释性进行了探讨分析。主要结论如下：

(1)基于波叠加法的声成像方法有利于充分利用声场的空间分布信息进行轴承故障诊断，且能够对声源进行定位。

(2)声像图与卷积神经网络的结合可以有效地解决人工特征提取困难、需要大量先验知识的问题，并且与其他两种基于声学故障诊断的常用方法进行对比时，具有较高的分类精度。

(3)对卷积神经网络分类结果进行了可解释性分析，验证了模型分类结果的可信度。

综上，本文提出了一种基于声成像与卷积神经网络的非接触式智能诊断方法，并初步验证了该方法分类结果的可解释性。该方法不仅可以用于文中的滚动轴承故障诊断，未来还能推广应用到其他类型的机械设备中，并且和降噪等信号处理方法结合用于更复杂的应用场景。该方法有望在振动测量受限的场合作为振动诊断技术的一种替代或有益补充。