基于改进PSO-BP神经网络的爆破振动速度峰值预测

范 勇，裴 勇，杨广栋，冷振东，2，卢文波

(1.三峡大学 湖北省水电工程施工与管理重点实验室，湖北 宜昌 443002；2.中国葛洲坝集团易普力股份有限公司 重庆市民用爆器材工程技术研究重心，重庆 401121；3.武汉大学 水工岩石力学教育部重点实验室，武汉 430072)

由于钻爆法的经济性和高效性，依然被广泛地应用于岩体破碎、矿山开采等方面。经研究，在爆破的过程中炸药所产生的能量只有20%～30%被利用，其余的70%～80%被以其他的方式浪费掉，并产生了多种负面影响，例如爆破飞石、爆破振动、空气超压等，其中爆破振动被认为对结构最有害的负面影响。

目前，爆破振动质点速度峰值(peak particle velocity，PPV)被用来评估爆破振动是否给结构带来破坏的重要指标。准确地预测PPV来优化爆破设计参数，可以有效降低爆破振动带来的不利影响[1]。以往的研究表明影响PPV的因素有爆破参数(如孔深、孔径、最大单响药量等)、岩体性质参数(如岩体的纵波波速[2]等)和地形地貌[3]。为了准确的预测PPV，许多研究学者提出了经验公式，如我国和俄国使用的是由前苏联学者提出的萨道夫斯基公式、美国使用的美国矿务局公式、印度使用的印度标准局公式等。但这些经验公式主要考虑了2个主要影响参数，即爆心距和最大单响药量，将其他影响参数归为了公式中的经验系数，已有的研究表明经验公式具有一定的局限性，存在预测的准确度低[4-5]。为了提高预测的准确度也有研究学者提出改正后的预测公式，如骆晓锋等[6]基于量纲分析理论在传统萨道夫斯基公式基础上提出反映高程变化的爆破振动的改进公式，并通过对比改进公式与萨道夫斯基公式的预测误差进一步论证改进公式的可靠性。

萨道夫斯基公式

(1)

式中:V为爆破振动质点速度峰值；r为爆心距；Q为最大单响药量；k，α分别为场地系数和衰减系数。

经验公式使用的影响因素有限，而且PPV与影响因素存在着复杂的非线性关系，预测的结果有时存在较大的误差，为了解决公式的不足，有必要使用新的预测方法。机器学习在解决非线性关系的问题上体现出明显的优势，而且可以将更多的影响因素作为输入参数，使得预测结果更加接近实测值。例如：Xu等[7]利用主成分分析从垂直距离、炸药类型、装药量等8个输入因子中提取前4个主成分作为输入参数，建立了GA-ANN(genetic algorithm-artificial neural network )预测模型，预测结果与实测值吻合更好；史秀志等[8]把最大单响药量、水平距离、高程差等作为输入参数，建立了基因表达式编程预测模型对PPV进行预测，结果表明比经验公式精度更高；邵良杉等[9]建立了LS-SVM(least squares support vector machine)预测模型，预测露天采矿爆破振动对民房的破坏情况，其结果与实际情况吻合较好；赵红梦等[10]建立了基于BP(back propagation)神经网络预测模型，预测结果更接近工程实测值。更多的研究表明[11-13]，BP神经网络适合PPV的预测。但是BP神经网络存在一定的缺陷，如初始权值和阈值的取值问题会使得预测的结果不稳定、准确度低等。目前，采用智能算法(如遗传算法(genetic algorithm，GA)[14]、粒子群算法等)来优化BP神经网络是一种有效的解决方法。

为了提高BP神经网络预测模型的准确度，采用了粒子群算法优化BP神经网络，建立改进的PSO-BP(particle swarm optimization-back propagation)神经网络预测模型，将其应用于爆破振动速度预测。针对BP神经网络输入参数的选择问题，当前，更多的研究是将爆破参数和距离作为主要的输入参数，缺少了对传播场地影响的考虑。本文以白鹤滩水电站左岸坝肩槽爆破开挖为依据，考虑了代表场地条件的纵波波速。对比BP神经网络以及萨道夫斯基公式检验结果，验证了该模型的合理性和适用性，为输入参数的选择提供了参考。

1 PSO-BP神经网络基本原理

1.1 BP神经网络

BP神经网络是一种按照误差逆向传播算法训练的多层前馈神经网络模型，具有很强的非线性映射能力。网络的结构包含着输入层、隐含层、输出层三部分，如图1所示。

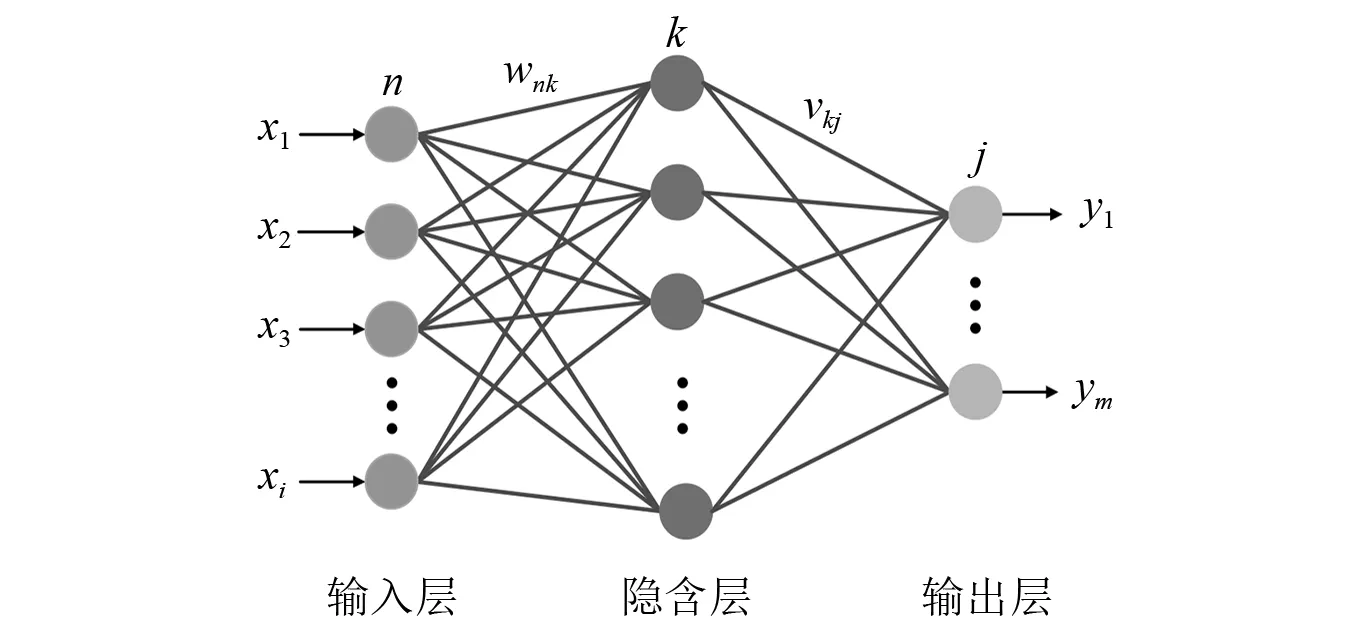
图1 3层BP神经网络拓扑结构Fig.1 The topology structure of 3-layer BP neural network

BP神经网络包括信号的正向传播和误差的反向传播2个过程。输入信号从输入层传入，经隐含层处理后传向输出层，若输出层的实际输出与期望输出不相符，则进入误差的反向传播。误差由输出层向前逐层反传，分配给各层神经元，连接神经元的权值和阈值通过各层获得的误差进行调整，其过程采用梯度下降法。经过反复的传播，当满足最小误差要求或者最大训练次数时，网络训练停止。

定义误差函数为

(2)

式中：Z为训练样本组数；m为输出层节点。

BP神经网络训练的步骤如下：

步骤1初始化网络权值wnk、vkj，阈值a、b。

步骤2计算隐含层神经元的输出值qk。

(3)

式中：k=1,2,…,h；f为隐含层激活函数；xn为第n个输入信号。

步骤3计算输出层神经元的输出值oj。

(4)

步骤4权值更新。

(5)

vkj(t+1)=vkj(t)+ηqk(yj-oj)

(6)

式中，η称为学习率的参数，一般取值(0，1)区间。

步骤5阈值更新。

(7)

bj(t+1)=bj(t)+(yj-oj)

(8)

步骤6判断算法是否迭代结束，若没有结束，则返回步骤2。

采用BP神经网络预测，需要确定隐含层数与其节点数。Hecht-Nielson在理论上已经证明单个隐含层的BP神经网络能够逼近任何区间的连续函数，所以本文神经网络选用单个隐含层结构。隐含层节点数采用经验式(9)[15],并根据训练集的均方误差(归一化后)最小值来确定隐含层节点数。

(9)

式中：h为隐含层节点数；i为输入层节点数；m为输出层节点数；a取1～10的整数。

1.2 粒子群算法原理

粒子群算法是由 Kennedy 和 Eberhart 于1995年提出的一种基于群体智能的优化方法，基本思想源于对鸟群捕食行为的研究。该算法首先在可行解空间初始化一群粒子，每个粒子代表一个优化问题的潜在解，用位置、速度和适应度值表示该粒子特征，粒子在每个维度的速度和位置变化范围限定在最大边界。群体中的粒子在每次迭代搜索过程中，通过跟踪群体的2个最佳位置不断地调整自己的速度和位置来搜索新解[16]。

假设在一个D维空间中，有n个粒子：

第i个粒子的位置：xi=(xi1,xi2,…,xiD),代表寻优问题在D维空间的一个潜在的解向量,将粒子i代入适应度函数求适应值；

第i个粒子的速度：vi=(vi1,vi2,…,viD)；

第i个粒子经历过的最佳位置：pbest=(pi1,pi2,…,piD)；

群种所经历过的最佳位置：gbest=(gi1,gi2,…,giD)；

粒子i的第d维速度和位置更新公式为

(10)

(11)

1.3 PSO-BP神经网络模型

BP神经网络虽然有很强的非线性映射能力，但误差的反向传播是基于梯度下降法来调整网络的连接权值和阈值，常常会陷入局部最优解，使得预测的准确度降低。PSO-BP神经网络模型利用了PSO算法的全局寻优能力，在其解空间内搜索网络的权值、阈值。粒子在每一维上的位置就是所求的解，要建立粒子的维数和权值、阈值的映射关系。单个隐含层的BP神经网络维数如下

D=i×h+h+h×m+m

(12)

式中：D为空间维数；i为输入层节点；h为隐含层节点；m为输出层节点。

粒子位置的优劣由适应度函数确定，文中选择训练集与测试集整体均方误差的平均值为适应度函数。适应度值越小，表明训练越准确，且兼顾模型的检验结果更好。适应度函数如下公式(单个输出节点)。

(13)

式中：Z，N分别为训练集、测试集样本组数；yp，op分别对应训练样本下输出层第p个实际输出和期望输出；Yl，Ol分别对应测试样本下输出层第l个实际输出和期望输出。

BP神经网络采用PSO算法优化后的权值和阈值进行训练和检验。具体流程图如图2所示。

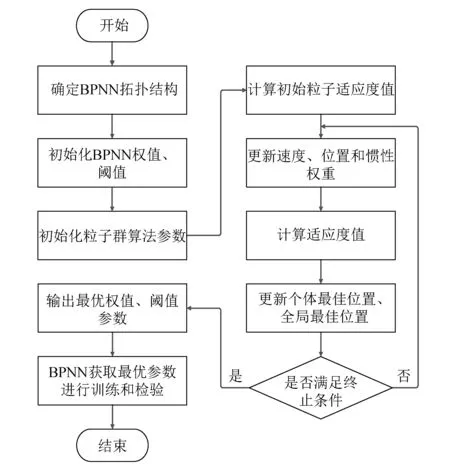
图2 PSO-BP神经网络流程图Fig.2 PSO-BP neural network flow chart

1.4 模型评估

在这项研究中，需要对模型进行评估。从统计学的角度来看，仅用一个性能指标进行评价是不够的。因此，采用决定系数(R2)、平均绝对误差(mean absolute error,MAE)、均方根误差(rooot mean square error,RMSE)和平均绝对百分比误差(mean absolute percentage error,MAPE)4个性能指标对模型综合评估。R2表示实测值与预测值的线性相关性，MAE用来表示结果的偏差，RMSE用来表示结果的离散度，MAPE表示结果的准确度。训练的评估采用R2、RMSE,检验的结果采用RMSE、MAE和MAPE进行评估[17]。计算公式为

(14)

(15)

(16)

(17)

2 爆破振动速度峰值预测

2.1 样本数据收集

2.1.1 工程概况

数据来自白鹤滩水电站左岸坝肩槽833.7 m，820.5 m，800.0 m，790.0 m和780.0 m爆破开挖所搜集到的63组数据集。白鹤滩水电站位于金沙江下游四川省宁南县和云南省巧家县交界的峡谷中，坝型为混凝土双曲拱坝，坝高289.0 m，设计正常蓄水位825.0 m，坝顶高程834.0 m，是金沙江下游4个梯级电站中的第二级。

金沙江该段总体由南向北流，左岸为大凉山山脉东南坡，整体上呈向金沙江倾斜的斜坡地形，岩体结构主要是在玄武岩岩流层中形成的层间、层内构造错动带以及断层构造裂隙系统，岩体的质量参次不齐，如图3所示。随着工程的进展，开挖揭示出新的地质条件。为确保坝肩槽岩体爆破开挖质量，设计了爆前、爆后声波检测，并开展了现场爆破振动监测工作，对每次爆破效果进行检测。目的是对爆破的效果进行评价，为坝肩槽的开挖提供合适的爆破参数。

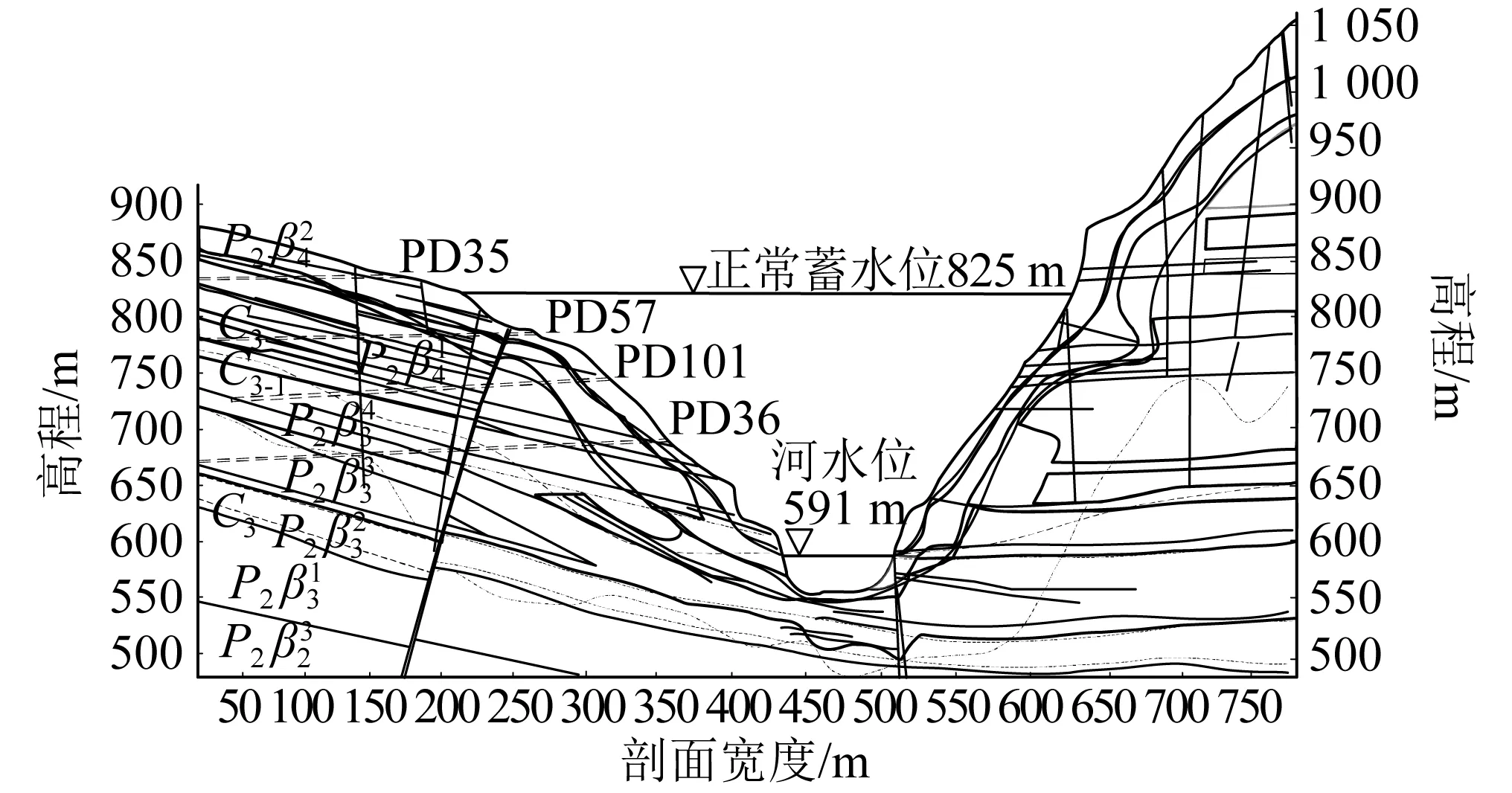
图3 白鹤滩水电站工程地质剖面图Fig.3 Engineering geological profile of Baihetan Hydropower Station

2.1.2 爆破振动监测

白鹤滩水电站爆破振动监测采用成都中科测控有限公司生产的爆破监测仪(TC-4850)。在监测点布置一台三向速度传感器(可同时测量竖直向、水平径向和水平切向PPV，文中采用的是水平径向PPV)，用石膏将传感器固定在所需监测的点位，然后将自记仪与其相联。爆破振动信号传递到监测点时，自记仪自动记录信号。爆后利用爆破振动分析软件将自记仪采集到的振动信号输入电脑中进行分析处理。

以高程820.5 m爆破开挖为例，根据现场地形条件，在爆区后方布置监测点如图4(a)所示，图4(b)中的数字分别代表测点编号及爆心距。现场爆破统一采用乳化炸药，起爆顺序为预裂孔、爆破孔、缓冲孔，预裂孔为5～7孔一响，爆破孔和缓冲孔为2孔一响，由于预裂孔先起爆产生预裂缝，削减了爆破孔和缓冲孔产生的爆破振动，在装药量上缓冲孔小于爆破孔，因此只关注预裂孔和爆破孔的爆破振动速度。具体的爆破参数如表1所示，炮孔布置如图4(c)所示。记录到的波形如图5所示。

图4 监测点及炮孔布置Fig.4 Layout of monitoring points and blasting parameters

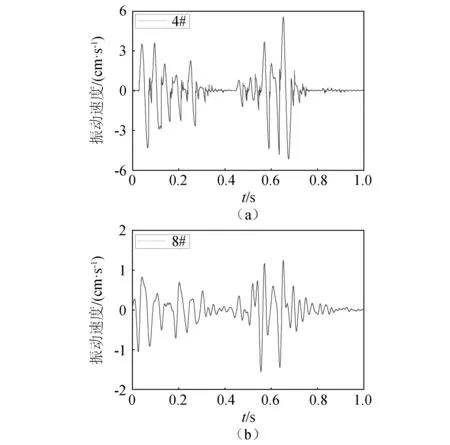
图5 水平径向振动波形Fig.5 Horizontal radial vibration waveform

表1 820.5 m爆破参数Tab.1 820.5 m blasting parameters

2.1.3 岩体声波检测

声波检测仪器为HX-SYB型智能型岩石声波仪，换能器为40 kHz单孔一发双收换能器。

具体声波检测步骤为：连好设备，将换能器置于检测孔底部，向检测孔注水至水流出；操作声波仪进行检测、读数并记录；移动换能器到下一检测位置，重复上述步骤。检测孔布置及现场爆前、爆后声波检测如图6所示(833.7 m声波检测)。检测到的纵波波速如图7所示。

图6 声波孔布置及现场声波检测Fig.6 Acoustic wave hole layout and field acoustic wave detection

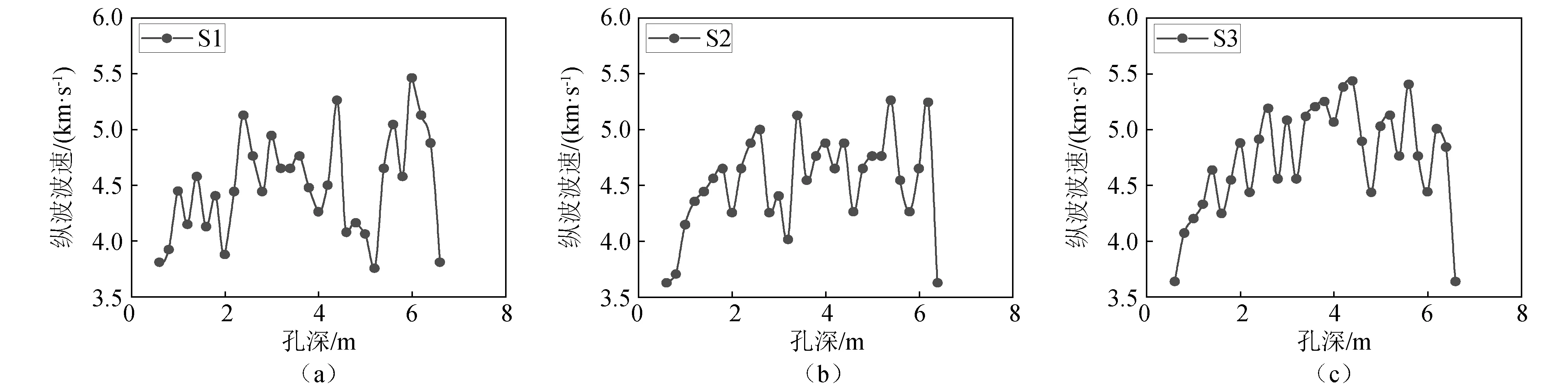
图7 爆后单孔纵波波速Fig.7 The longitudinal wave velocity of single hole after explosion

2.2 模型参数的选择

输入参数的选择是BP神经网络一个重要因素。为了建立一个全面而准确的模型，需要确定影响PPV的主要输入参数，同时应考虑所选参数必须代表现场条件和爆破设计参数必须是可获的。

表2、表3是白鹤滩水电站左岸坝肩槽高程833.7 m与高程817.0 m两次爆破开挖收集到的爆破振动数据，两次爆破地形不同。采用萨道夫斯基公式拟合。

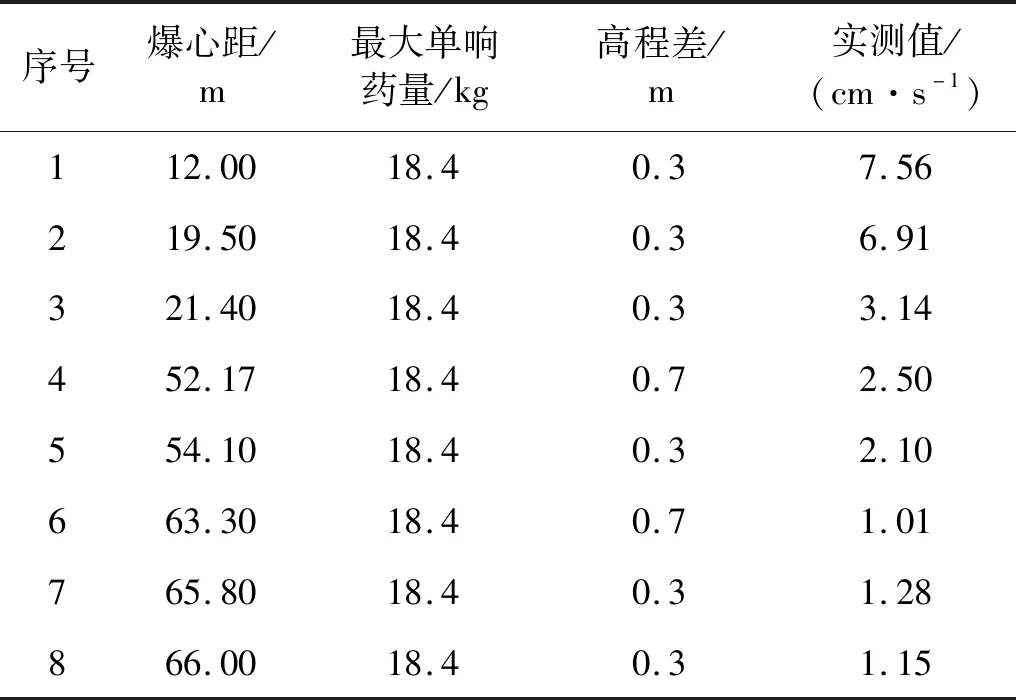
表2 833.7 m预裂爆破振动数据Tab.2 833.7 m vibration data of presplitting blasting

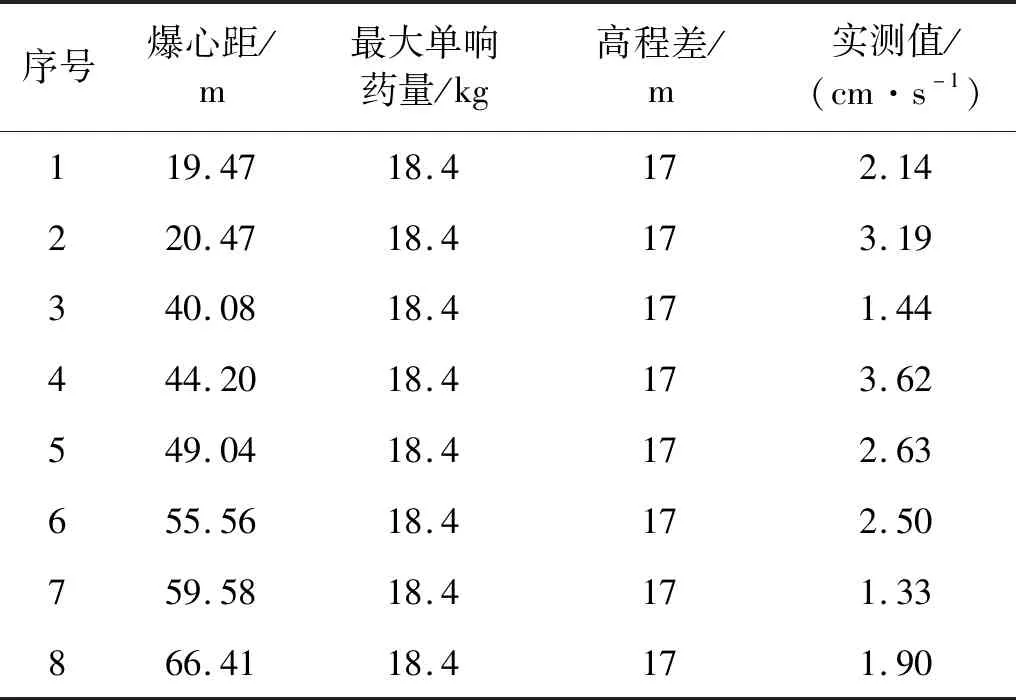
表3 817 m预裂爆破振动数据Tab.3 817 m vibration data of presplitting blasting

将萨道夫斯基公式两边取对数转化为线性公式

(18)

y=∂x+b

(19)

采用最小二乘法对两次爆破振动数据进行回归拟合，拟合结果如图8所示。

图8 萨道夫斯基公式拟合曲线Fig.8 Curve fitting of Sadovsky formula

高程833.7 m和817.0 m拟合的相关系数分别为R2=0.863，R2=0.104。从拟合的结果可以得出，采用萨道夫斯基公式预测监测点与爆区在同水平面的PPV具有很好的适用性。当爆区与监测点产生高差时，萨道夫斯基公式并不再适用于预测PPV。因此，将高程差(H)作为一个影响参数。

通过拟合得到高程833.7 m的系数k=41.513，α=1.068。回归分析后得到的萨道夫斯基公式为

(20)

采用高程833.7 m拟合得到的k、α对高程817.0 m的PPV预测，预测结果如表4所示。

表4 817.0 m PPV实测值与预测值对比Tab.4 Comparison between measured value and predicted value of 817.0 m PPV

从表4实测值与预测值的对比结果可以看出，误差整体在30%以上，准确度低。可以得出振动速度在传播的时候受到了场地条件的影响。纵波波速可以很好的反应岩体的裂隙、结构面发育情况等场地特征。因此，将纵波波速作为振动速度传播的影响参数。本文采用的是爆破后所测得的6个检测孔的平均值作为输入参数。

经分析选择了爆心距、最大单响药量、高程差和纵波波速作为预测模型的输入参数。

2.3 敏感性分析

为识别各输入参数对PPV的相对影响，采用Yang等[18]提出的余弦振幅法进行敏感性分析，评估输入参数对PPV的影响。两者之间的关系强度(rij)由式(21)表示

(21)

式中：m为数据个数(文中数据为63组)；xik，xjk分别为输入参数和输出参数。每个输入参数的rij值在0～1变化，最高的rij值表示对PPV最有影响的参数。输入参数与输出参数的关系强度计算结果如图9所示。

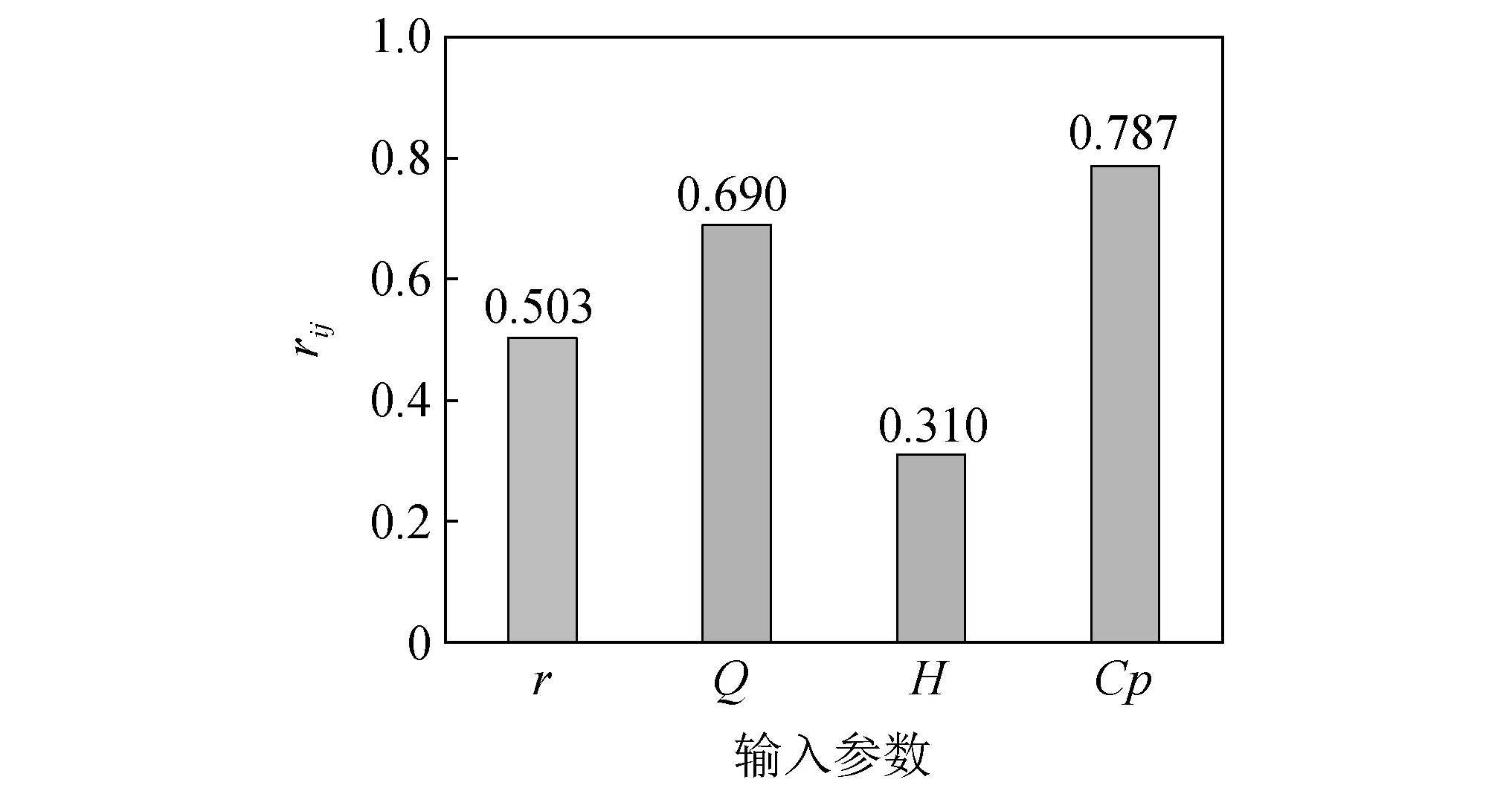
图9 输入和输出参数之间的关系强度Fig.9 The strength of the relationship between input and output parameters

敏感性分析结果表明，在传播的过程中代表场地条件的纵波波速对PPV的影响最显著，其次是最大单响药量、爆心距，高程差对PPV影响最小。

2.4 预测方法训练

基于MATLAB语言构建的预测模型，输入层节点数为4(即爆心距、最大单响药量、高程差和纵波波速)，输出层节点为一个(即PPV)，隐含层节点数采用经验公式(9)，得到[3,12]10个不同的节点数，每次运行通过对比不同节点数得到训练集的均方误差来选取节点数。

BP神经网络参数设置，训练次数1 000，学习速率0.01，最小误差1×10-6，隐含层选用Tansig函数，输出层为purelin函数，训练函数采用trainlm。

将所收集到的63组数据集随机排序，选取前53组作为训练集进行训练，后10组为测试集进行检验。训练前对数据进行归一化处理，归一化可以消除特征指标的量纲和数量级的影响，有助于提高网络的学习速度，对于检验后的数据还要进行反归一化。利用式(22)归一化，区间为[0,1]。

(22)

式中：i为归一化后的输入数据；x为实测数据；xmin，xmax分别为实测数据中的最大值与最小值。

2.4.1 PSO-BP神经网络预测模型

PSO-BP神经网络预测模型的最佳性能与其惯性权重ω、加速度常数c1，c2和种群规模有着直接的影响，需要对参数合理的选取，收敛性分析[19]的讨论为参数选择提供了依据。

对式(10)、式(11)可简化到一维

v(k+1)=ωv(k)+φ1[pbest-x(k)]+
φ2[gbest-x(k)]

(23)

x(k+1)=x(k)+v(k+1)

(24)

则参数ω，φ需满足

ω<1,φ>0,2ω-φ+2>0

(25)

文章选取粒子群规模为200，最大迭代次数1 000，以达到搜索全局的目的。惯性权重ω体现了粒子继承先前速度的能力。针对PSO算法容易早熟以及算法后期易在全局最优解附近产生振荡现像，研究学者提出自适应调整的PSO算法，让ω随着算法的迭代而递减。常见的有以下4种方法[20-21]。

(26)

(27)

(28)

(29)

式中：ωmax为惯性权重最大值；ωmin为惯性权重最小值；k为当前迭代次数；Tmax为最大迭代次数。研究表明，当惯性权重ωmax=0.9，ωmin=0.4时算法性能最好。

针对4种不同的ω进行算法性能分析。为了减少模型中随机数的影响，设置了随机种子，对不同的惯性权重预测模型都具有相同的随机数，选取加速度常数c1=c2=2，分析结果如表5所示。

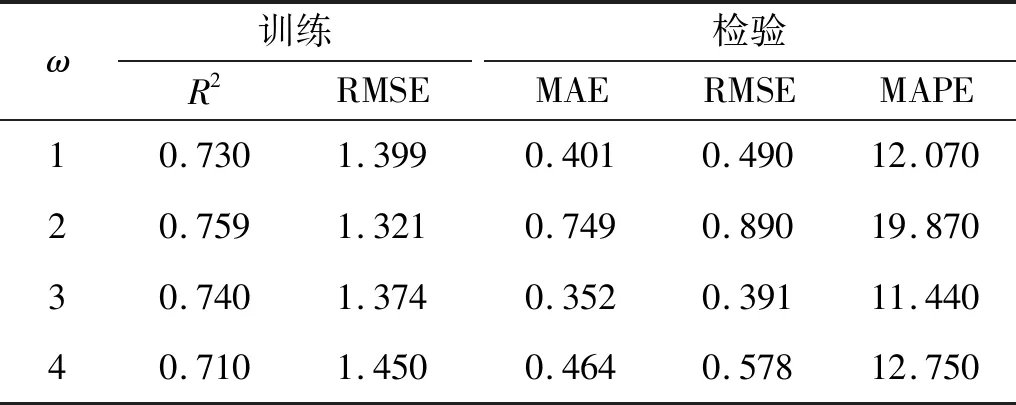
表5 4种惯性权重下的算法性能比较Tab.5 Performance comparison of algorithms under 4 inertia weights

从表5和图10得到的检验结果和最小适应度值对模型综合分析，选取ω3作为惯性权重来改进PSO算法。

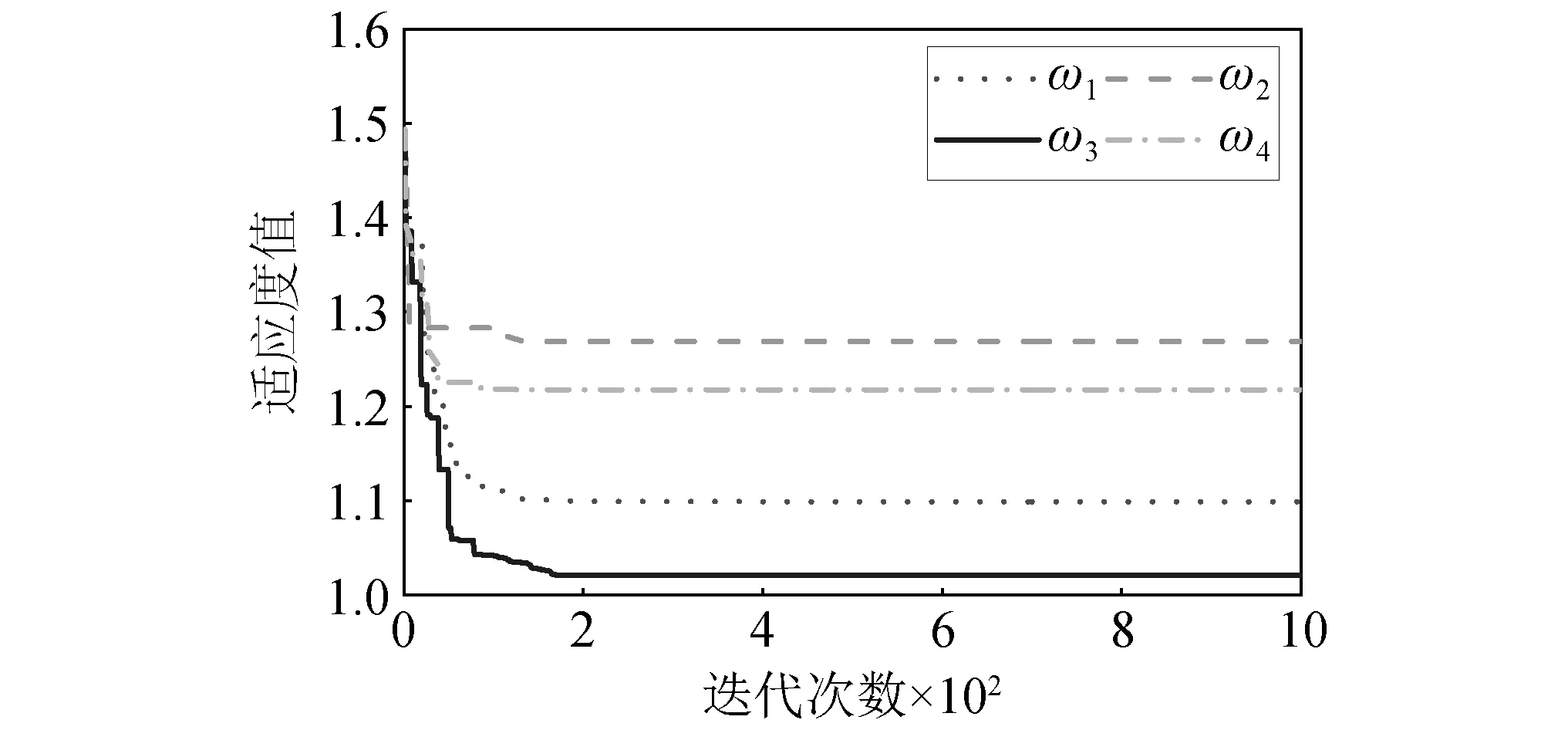
图10 4种惯性权重的收敛曲线Fig.10 Convergence curves of 4 inertia weights

选取ω3作为惯性权重，加速度常数c1，c2采取不同比值[22]情况下的取值。对于不同加速度常数模型的训练结果如表6所示。

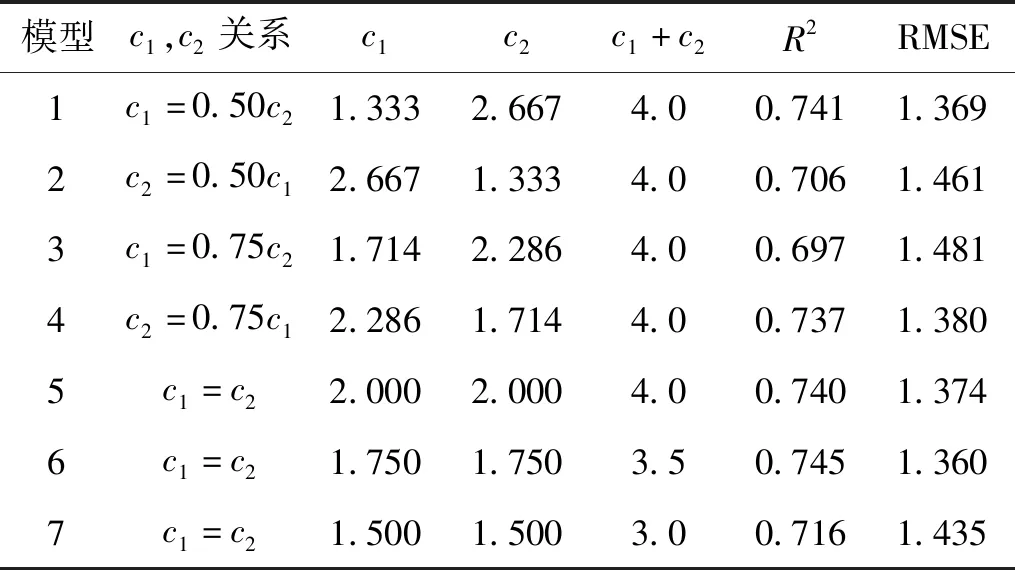
表6 7种不同加速度常数模型训练评估Tab.6 Training evaluation of 7 different acceleration constant models

2.4.2 BP神经网络预测模型

由于BP神经网络误差的反向传播采用的是梯度下降法，易陷入局部最优，因此，采用多次预测的方法。文中采用3次预测，选取最优结果。对每次训练结果评估如表7所示。

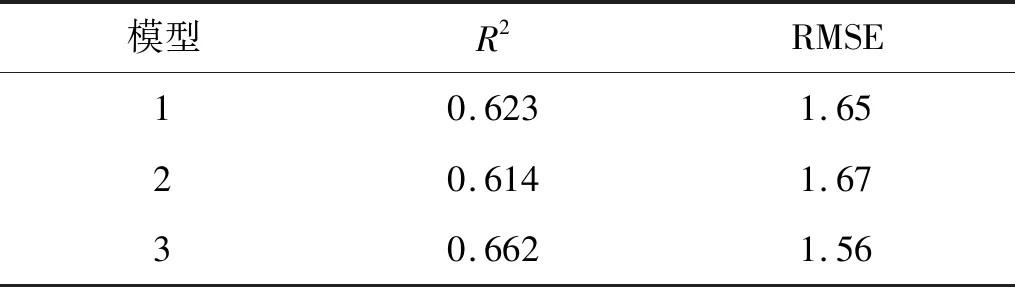
表7 模型训练评估Tab.7 Model training evaluation

2.5 预测方法检验

每次训练后，采用后10组测试集进行检验，并对不同模型检验的结果进行评估。BP神经网络和改进的PSO-BP神经网络预测模型的检验结果如表8、表9所示。

由表8可以得出，BP神经网络预测模型3检验结果最好。由表9检验结果和不同加速度模型的收敛曲线如图11综合评估，改进的PSO-BP神经网络预测模型6检验结果最优。两种方法隐含层节点得选取如下表10、表11，通过选取的结果可以发现8个隐含层节点是网络模型的最优节点，搭建了4×8×1的网络拓扑结构。此外，由检验结果可以得出，改进的PSO-BP神经网络预测模型的准确度均好于BP神经网络预测模型，说明了改进的PSO算法具有较好的优化能力。

表8 BP神经网络检验结果Tab.8 BP neural network test results

表9 改进的PSO-BP神经网络检验结果Tab.9 The test results of the improved PSO-BP neural network

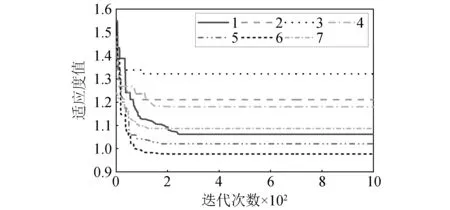
图11 7种不同加速度常数模型的收敛曲线Fig.11 Convergence curves of 7 models with different acceleration constants

表10 BP神经网络预测模型3隐含层节点选取Tab.10 BP neural network model 3 hidden layer node selection

表11 改进的PSO-BP神经网络预测模型6隐含层节点选取Tab.11 Improved PSO-BP neural network model 6 hidden layer node selection

2.6 萨道夫斯基公式预测

利用萨道夫斯基公式回归分析。将前53组数据进行回归拟合，对后10组检验。得到的拟合曲线如图12所示。

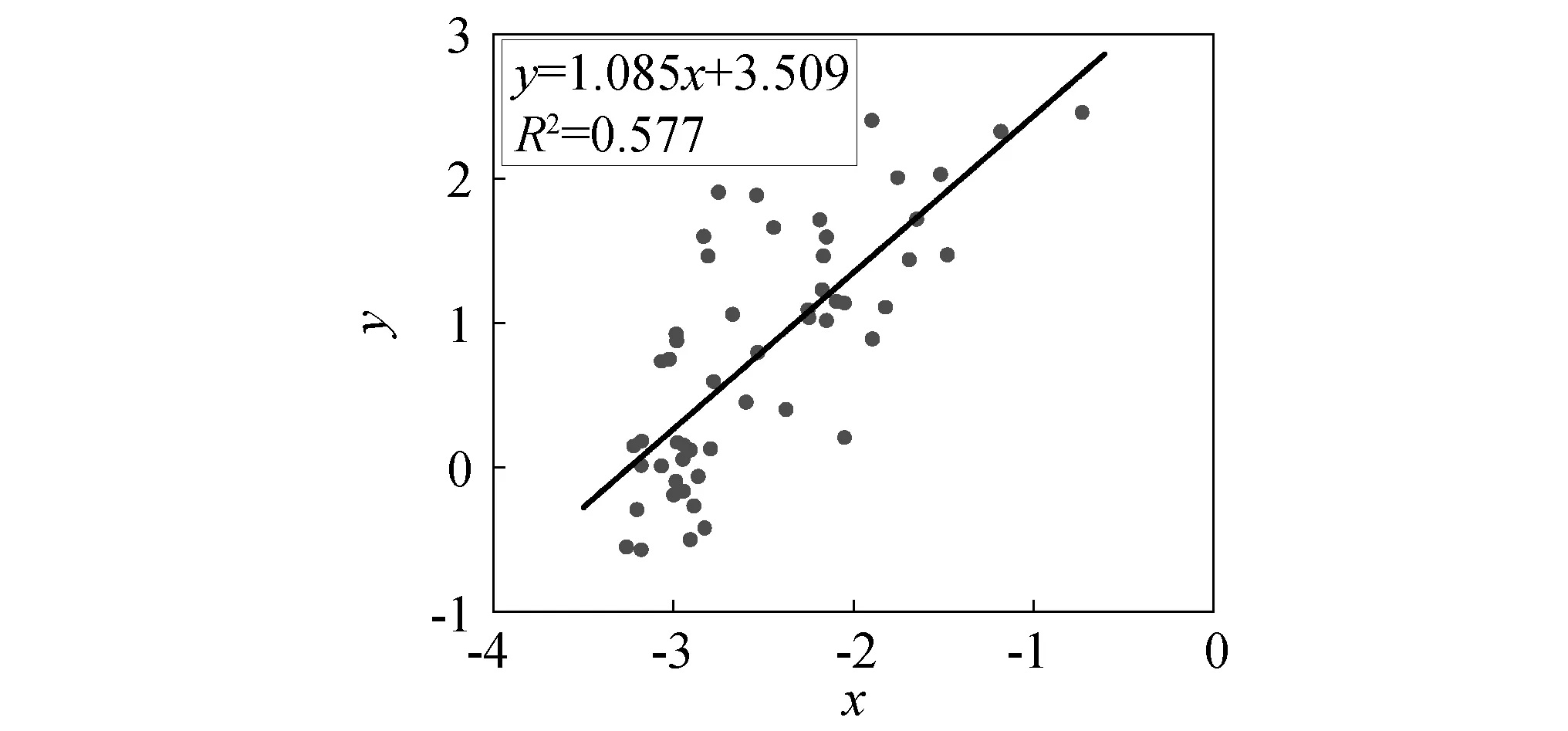
图12 拟合曲线Fig.12 Curve fitting

通过拟合得到k=33.428，α=1.085，相关系数为0.577。回归分析后得到的萨道夫斯基公式为

(30)

对后10组的检验结果如表12所示。

表12 检验结果对比分析Tab.12 Comparative analysis of test results

3 结果分析

萨道夫斯基公式、BP神经网络预测模型3和改进的PSO-BP神经网络预测模型6对后10组检验的结果对比见表12和图13。

图13 检验结果对比图Fig.13 Comparison chart of test results

由表12和图13可得，改进的PSO-BP神经网络预测模型的最大误差为20.94%，MAPE为8.27%；BP神经网络预测模型的最大误差为44.45%，MAPE为18.71%；萨道夫斯基公式检验的最大误差为78.74%，MAPE为32.56%，准确度最低。对比BP神经网络预测模型和萨道夫斯基公式的检验结果，改进的PSO-BP神经网络预测模型的准确度更高，与真实值接近，具有较好的泛化能力。

4 结 论

影响PPV的参数较多，而且存在复杂的非线性关系，采用经验公式预测准确度低。本文建立了改进的PSO-BP神经网络预测模型，将其应用于白鹤滩水电站左岸坝肩槽爆破开挖PPV的预测，并与BP神经网络及萨道夫斯基公式检验结果比较，初步得出以下结论：

(1) 采用改进的PSO-BP神经网络预测模型，选取了爆心距、最大单响药量、高程差和纵波波速作为输入参数，PPV作为输出参数，通过分析建立的网络拓扑结构为4×8×1的最佳性能模型，检验结果MAPE为8.27%，远好于BP神经网络预测的最佳结果18.71%和萨道夫斯基公式32.56%。检验结果表明改进的PSO算法优化BP神经网络预测模型具有较好的泛化能力，可有效的应用于实际工程预测PPV。

(2) 采用余弦振幅法分析爆心距、最大单响药量、高程差和纵波波速与PPV的关系强度分别为0.503，0.690，0.310和0.787，结果表明PPV在传播的过程中，代表场地条件的纵波波速对PPV影响最显著。萨道夫斯基公式仅将爆心距和最大单响药量作为主要影响参数，检验的结果误差较大，准确度低，不再适用于PPV的预测。

(3) 与经验公式相比，BP神经网络在处理非线性关系时具有较好的性能，而且可以较全面考虑影响PPV的参数，使得预测结果与实际值更加吻合。