超空泡射弹异步并联入水流场与运动特性研究

闫雪璞，鹿 麟，王 辰，李 强，胡彦晓

(中北大学 机电工程学院，太原 030051)

超空泡射弹凭借其优秀的水下减阻性能，被广泛应用于反水雷及反蛙人行动中。并联发射超空泡射弹可以显著提高发射效率、增大毁伤概率以及提升杀伤效果，但在实际应用中，超空泡射弹异步并联入水更为常见。而在两弹丸异步并联入水的过程中，弹丸不仅会受到强湍流、多相流以及冲击载荷的影响，还会受到异步并联弹丸之间相互扰动的影响，从而表现出较强的瞬时性和非定常性，因此对异步并联超空泡射弹入水问题开展研究很有必要。

目前，国内外学者已经对超空泡射弹入水问题做了很多深入研究，但其中大多是针对单发超空泡射弹。黄闯等[1]研究了液体可压缩性对跨声速超空化流动的影响。陈晨等[2-3]针对在不同空气域压力下的高速射弹入水问题开展了研究，发现了空气域压力对喷溅形态和空泡表面闭合时间等影响较大。王云等[4]通过试验分析了4种头型弹丸以不同入水角及速度入水后的弹道特性。侯宇等[5]对超空泡射弹以不同侧滑角入水时的喷溅演变及压力场分布进行了试验研究。Li等[6-7]研究了弹丸的旋转速度、初速度及入水角度对弹丸运动特性的影响规律。Techet等[8]研究了长径比对弹丸入水运动特性的影响。Erfanian等[9]对一种球形头部弹丸的入水过程进行了仿真模拟。Lee等[10]分析了入水速度对相同尺寸弹丸发生深闭合的时间及位置的影响。Weiland等[11]开展了圆柱体高速入水试验并分析了其空泡发展规律，发现了驱动气体促使超空化加速发生的现象。

相较于单发超空泡射弹，针对并联超空泡射弹开展的研究尚不多见。余德磊等[12]分析了入水速度、初始净距及横流速度对回转体并联入水过程的影响。路丽睿等[13]对回转体并联入水开展了试验，并将试验结果与回转体单独入水进行了对比分析。王旭等[14]研究了不同横向间距的双球入水后的空泡演化及运动特性，以上研究都没有涉及流场变化更为复杂的超空泡射弹异步并联入水问题。张鹤等[15]虽对圆柱体单独入水及异步并联入水进行了试验研究，但研究着重于入水时差对空泡表面闭合时间的影响，且回转体入水速度较低。

本文针对异步并联射弹高速入水问题，开展了单发超空泡射弹倾斜入水试验，并将试验结果与仿真结果对比，验证了数值方法的可靠性。基于重叠网格技术，利用数值建模的方法研究了初始纵向间距分别为0，0.5，1.0，1.5，2.0及3.0倍弹长时，异步并联超空泡射弹流场特性、稳定性及减阻特性的变化规律。研究结果可为超空泡射弹的弹道预测提供参考依据，具有一定的工程意义。

1 数值模拟方法

1.1 控制方程

本文在数值计算时采用了VOF多相流模型进行模拟，用αl，αg，αv分别表示水、空气和水蒸气的体积分数，满足αl+αg+αv=1。

混合相的连续性方程为

(1)

混合相的动量方程为

(2)

ρm=αlρl+αgρg+αvρv

(3)

μm=αlμl+αgμg+αvμv

(4)

式中：t为时间；ui和uj分别为在i和j方向上的速度分量；xi和xj为位移分量；ρm为混合相密度；μm为混合相动力黏度。

湍流模型采用Realizablek-ε模型，该模型在Standardk-ε模型的基础上引入了新的湍流黏度计算公式，擅长计算旋转漩涡、强弯曲流动等情况，并被广泛应用于带旋转的剪切流、边界层流动及自由射流等计算中。同时该模型考虑了平均流动扰动对湍流耗散的影响，具有较高的数值精度和稳定性。

1.2 空化模型

本文在数值计算时采用文献[16]中的Zwart-Gerber-Belamri(Z-G-B空化)模型模拟空化现象，其蒸汽输运方程如下

(5)

(6)

(7)

式中：v为汽相；ρv为饱和蒸汽压；Re和Rc分别为每单位体积的蒸发和冷凝速率；RB为气核半径；αnuc为汽核体积分数；Fvap为汽化系数；Fcond为冷凝系数。

1.3 数值方法验证

考虑到高速弹丸异步并联入水试验难度较大，而在已公开的文献中又难以获取相关试验数据。本文在验证数值计算方法的准确性时，一方面利用高速摄像机及入水试验装置对单发射弹高速倾斜入水开展试验，同时使用前文建立的数值方法对相同工况的射弹入水进行仿真模拟，最终将仿真结果与试验数据进行对比验证；另一方面对文献[17]中弹丸同步并联入水的过程进行验证。

1.3.1 单发射弹高速倾斜入水数值方法验证

试验设备布置情况如图1所示，试验设备主要包括敞口水箱、发射系统、高速摄影机、计算机及照明系统。敞口水箱尺寸为3.0 m×2.0 m×2.0 m，前后两侧为钢化玻璃，其他侧壁由15 mm钢板和钢制支架组成，箱底铺设有25 mm松木板与6 mm钢板复合捆扎而成的接弹缓冲装置，试验时注入水深1.2 m，为保证水质清澈，用明矾对水箱做沉淀处理。发射系统由轻气炮发射装置与发射控制装置组成，轻气炮发射装置放置在水箱右侧，连接的高压氮气瓶为弹丸发射提供动力；发射控制装置由控制器和电磁气阀组成，主要负责弹丸击发与高速摄像机时序控制。在水箱正面布有FASTCAM SA-X2型高速摄影机，采集帧率为7 200 fps，分辨率为1 024×1 024像素，使用计算机可控制高速摄影机完成试验数据采集工作。水箱背面设有照明系统，其中LED灯板起补光作用，灯板与水箱间的柔光屏可以提高拍摄画面质量。在拍摄范围内设有网格尺寸为50 mm×50 mm的方形坐标尺，用于校准试验测试结果。

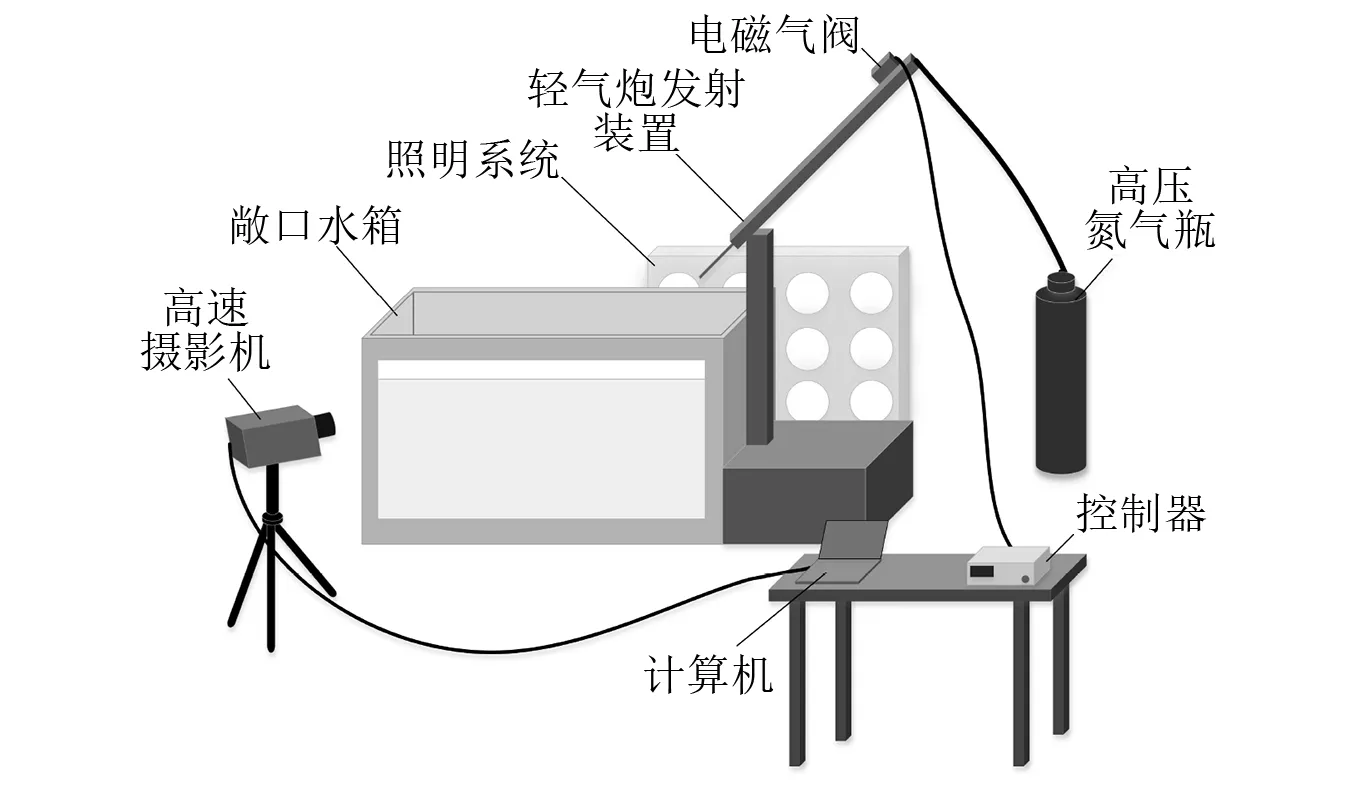
图1 试验设备布置Fig.1 Scheme of experimental equipment

试验中使用的弹丸及计算域设置如图2所示，所用弹丸材质为钢，质量为0.012 6 kg。初始时刻弹丸位于空气域中，入水速度及入水角度对应试验分别为226.58 m/s和60°。图3给出了网格划分示意图，最终得到的网格总数为80万。图4给出了四个不同时刻的空泡形态对比图，从图中可知试验结果和仿真结果基本吻合。再由图5的速度随时间衰减曲线可以看出，两条曲线在衰减过程中呈现相同趋势，最大误差为0.4%。

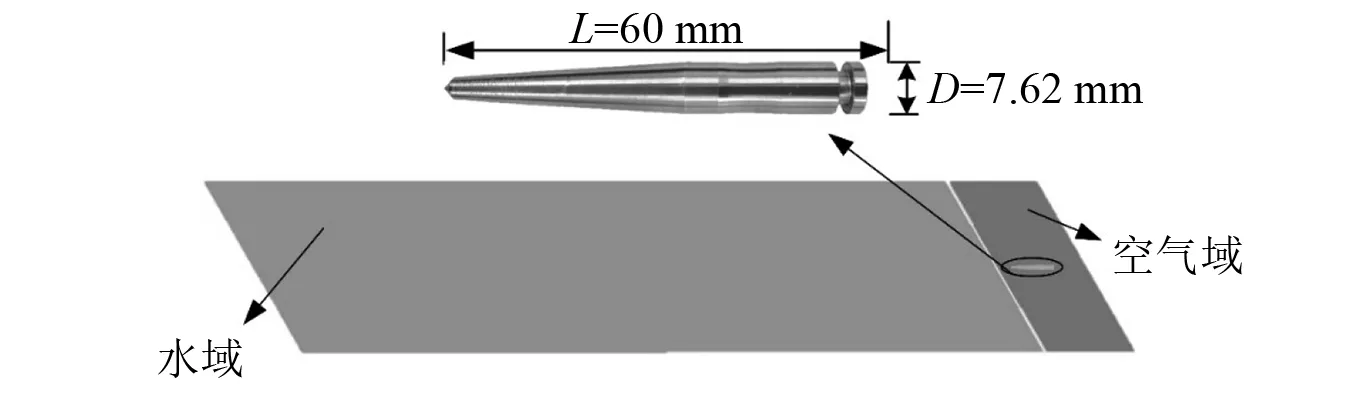
图2 单发弹丸模型及计算域设置Fig.2 Experimental projectile model and calculation domain

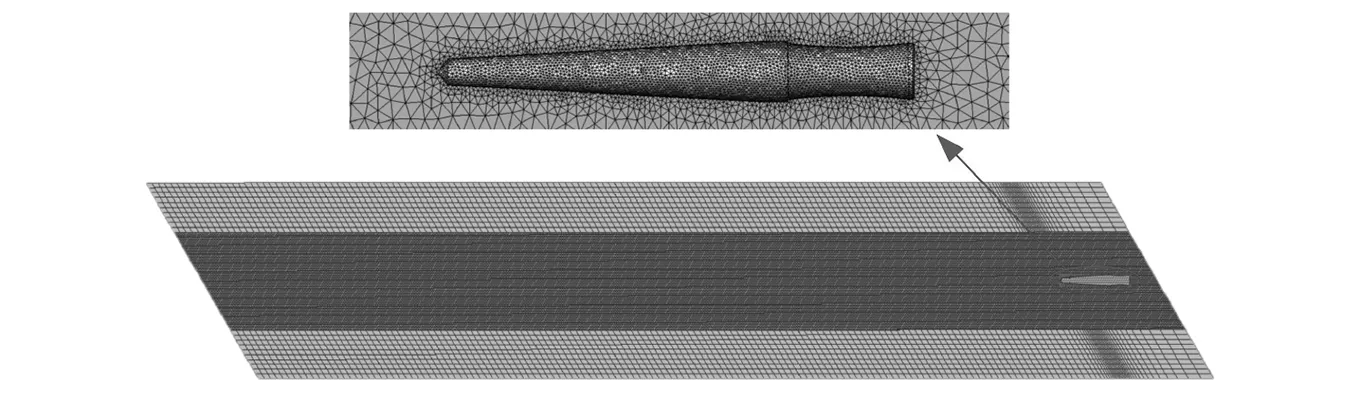
图3 单发弹丸入水网格划分Fig.3 Grid generation of water entry of single projectile

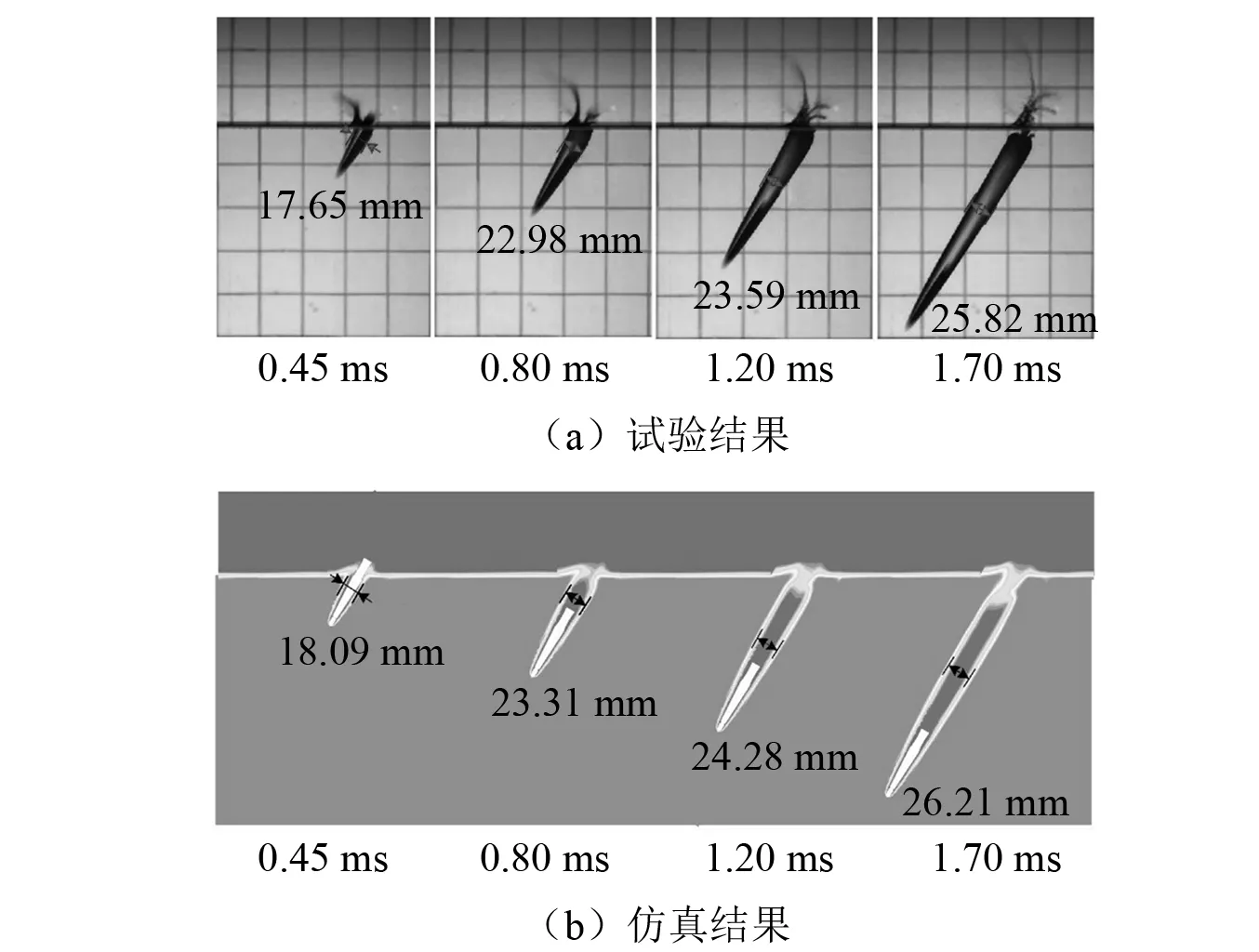
图4 单发弹丸空泡形态仿真与试验结果对比Fig.4 Comparison of simulation and experimental results of cavitation of single projectile

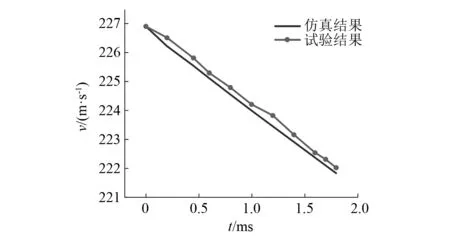
图5 单发弹丸速度衰减仿真与试验结果对比Fig.5 Comparison between simulation results of velocity attenuation of single projectile and experimental results

1.3.2 同步并联射弹入水数值方法验证

为进一步验证数值方法的准确性，本文使用前文所述的数值仿真方法对张鹤等研究中的弹丸同步并联入水过程进行验证。弹丸的结构及网格划分示意图如图6所示，弹丸质量为0.179 kg，初速为81.2 m/s。从图7可以看出，在三个不同时刻由试验与数值计算得到的流场形态基本相同。图8给出了由试验和数值仿真结果得到的弹丸速度随时间变化图，从图中可知试验结果与仿真结果基本拟合。

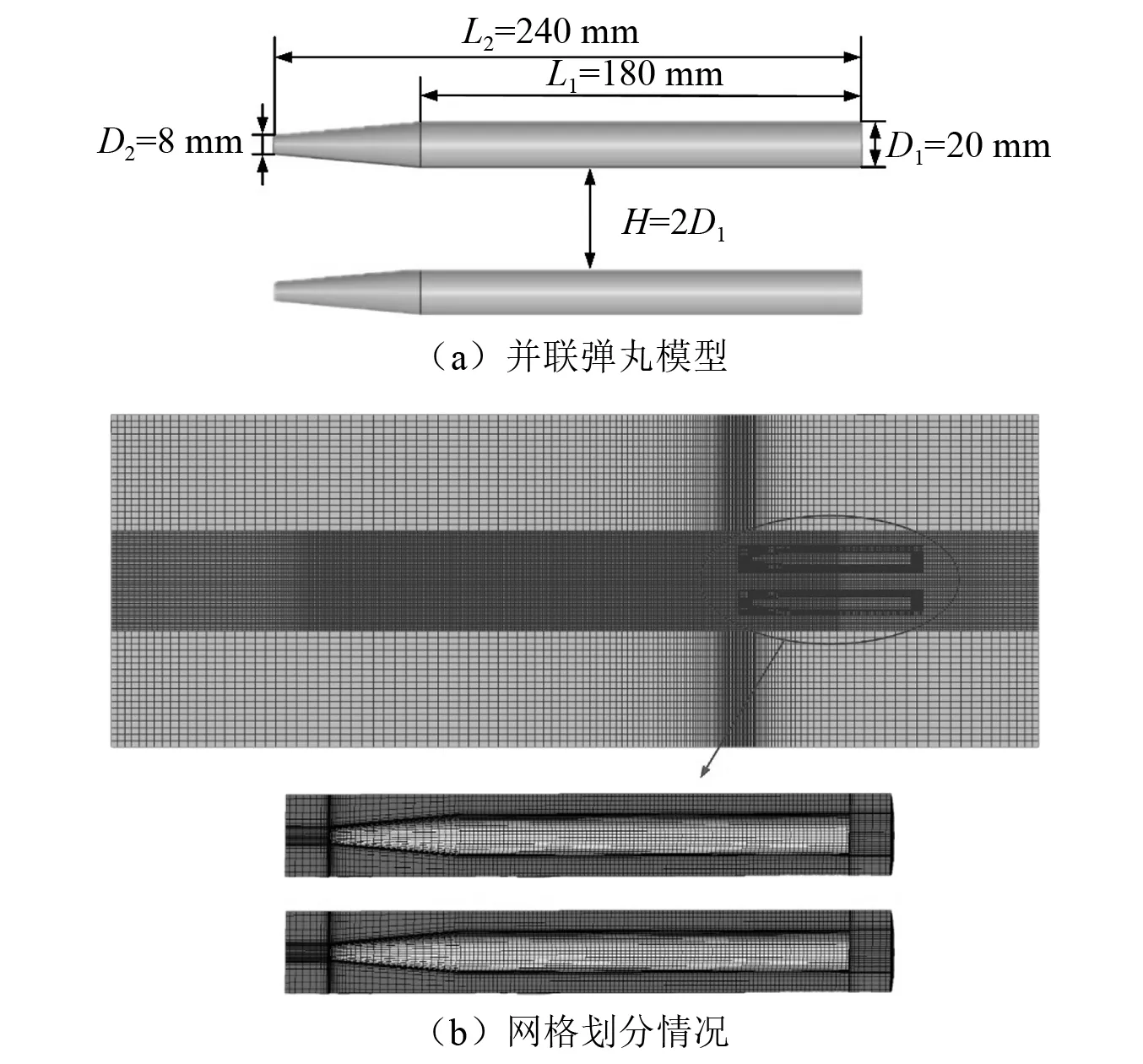
图6 并联弹丸模型与网格划分Fig.6 Parallel projectile model and grid generation

图7 并联弹丸空泡形态仿真与试验结果对比Fig.7 Comparison of simulation and experimental results of cavitation of parallel projectile

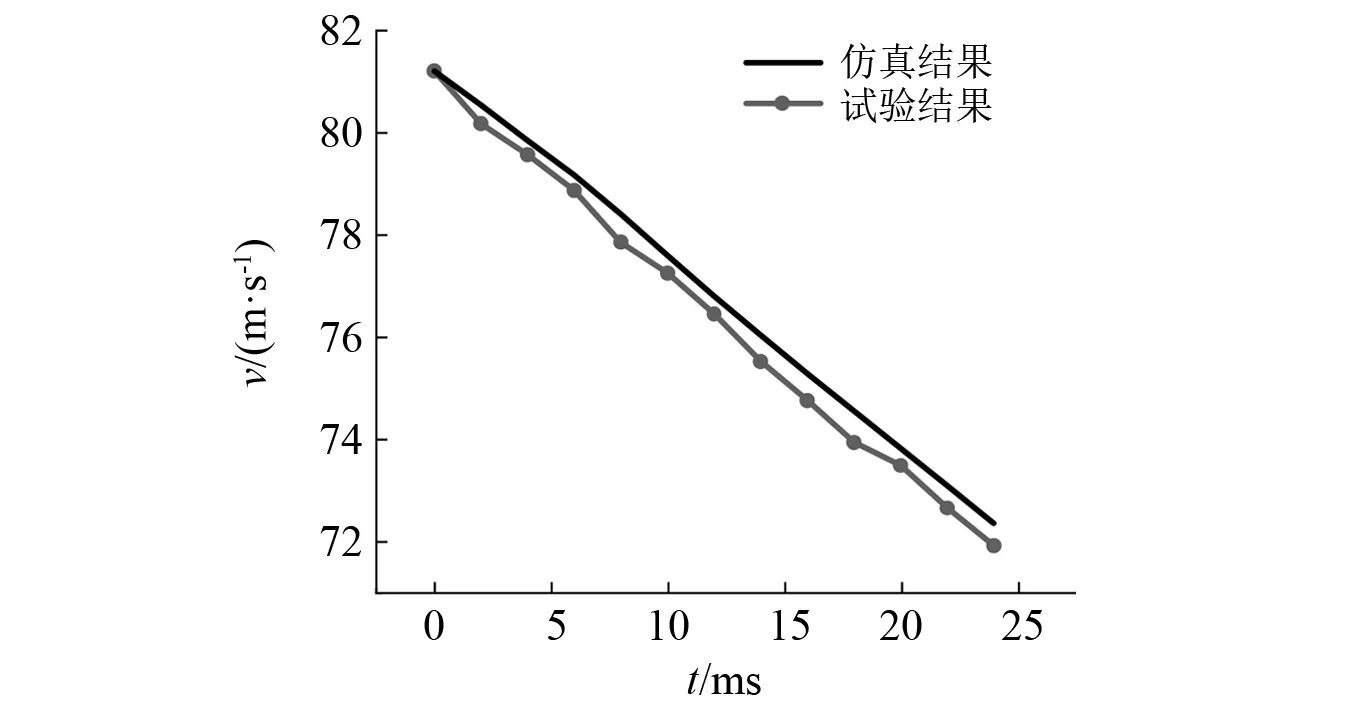
图8 并联弹丸速度衰减仿真与试验结果对比Fig.8 Comparison between simulation results of velocity attenuation of parallel projectile and experimental results

1.4 计算模型与网格划分

本文选用的计算模型为头部带有圆锥形空化器的两发并联超空泡射弹，两发射弹的外形尺寸及物理参数完全相同，如表1所示。射弹的结构示意图如图9所示，不同工况两发射弹的初始横向间距皆为7.62 mm，初始纵向间距为L，定义无量纲量K=L/D，工况设置为K=0，K=0.5，K=1.0，K=1.5，K=2.0及K=3.0。为了便于后文分析定义左侧先入水弹丸为弹1，右侧后入水弹丸为弹2；弹1头部接触自由液面时刻t1=t2=0；两弹丸相隔较近一侧为内侧，相隔较远一侧为外侧。

表1 异步并联弹丸模型尺寸Tab.1 Model dimensions of asynchronous parallel projectiles

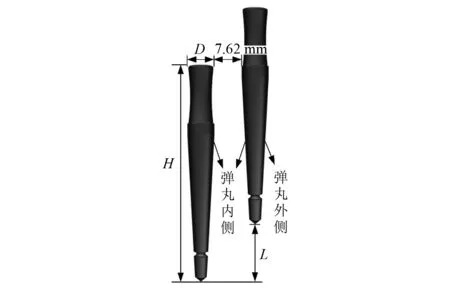
图9 异步并联计算模型示意图Fig.9 Diagram of asynchronous parallel computation model

图10(a)给出了初始时刻两发弹丸的空间位置及计算域的总体尺寸，计算域为总体尺寸70D×35D×150D的长方体，足够避免边界效应。初始时刻两发弹丸均位于自由液面上方空气域中，空气域高度为50D，水域高度为100D，弹1头部与自由液面间距离为1D。坐标系位置及流场边界条件设置情况如图10(b)所示，坐标原点落在对称轴上，设置在自由液面上方1D处，Z轴负方向为弹丸运动方向。设置边界条件时射弹采用壁面条件，计算域上下两端为压力出口边界，在对称面上设置对称面边界条件，其余为壁面条件。

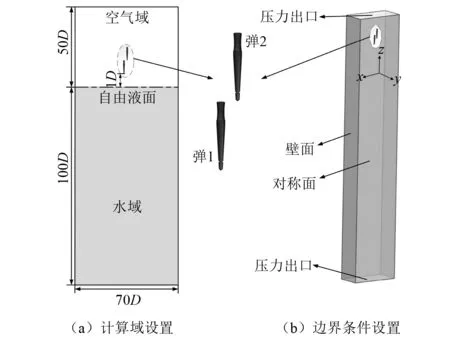
图10 异步并联计算域及边界条件设置Fig.10 Calculation domain and boundary condition setting of asynchronous parallel

本文针对高速射弹入水选用了重叠网格技术，考虑到计算模型为轴对称模型，本文仅对流体计算域的一半进行了网格划分。重叠网格技术需提前准备前景网格及背景网格两套计算网格，图11(a)给出了前景网格局部示意图，本文在两枚射弹周围分别划分了非结构化前景网格，射弹表面网格尺寸0.5 mm。并且为了得到弹体周围准确的流场变化规律，划分时在弹体表面生成了4层棱柱体网格，第一层网格的y+值控制在30左右。背景网格整体划分如图11(b)所示，网格类型采用六面体网格，在液面及射弹运动区域附近都进行了局部网格加密，有利于捕捉液面喷溅的产生和加强仿真结果的可靠性。为了节约计算资源，在运动区域外部布置了较少的网格节点，最终网格总数为140万。此外，本文采用有限体积法对控制方程进行离散求解，对压力-速度耦合方程求解时采用了Coupled算法，对压力场进行空间离散时采用了PRESTO!格式。

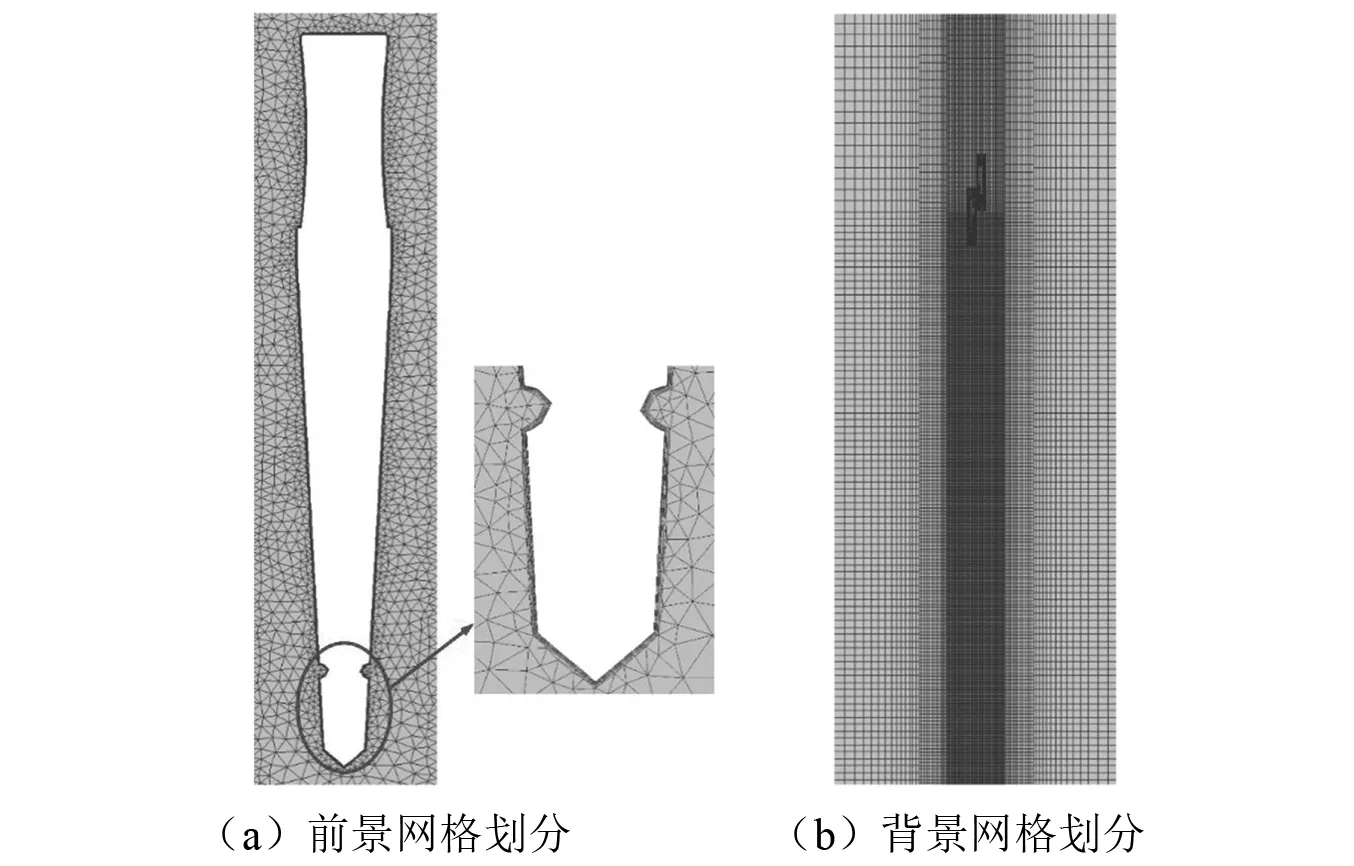
图11 异步并联网格划分Fig.11 Grid generation of asynchronous parallel

1.5 网格无关性验证

为了使数值模拟达到较高的精度，本文在不改变总体网格划分规律的前提下，通过调整射弹运动区域及弹丸附近网格密度，得到了网格总数分别为100万、140万及200万的三套网格。设置相同的时间步长2×10-6s，以此对初速400 m/s、K=1.5的异步并行入水进行了数值模拟。图12给出了不同网格密度下弹1水下速度衰减曲线，从图中可知，140万网格和200万网格在相同时刻速度差值极小，综合考虑计算的准确度和时间成本后，本文选用网格数140万的网格进行计算。

图12 不同网格密度下弹丸速度衰减曲线Fig.12 Projectile velocity attenuation curve under different grid density

2 计算结果与讨论

2.1 异步并联入水流场形态特性分析

本文使用水体积分数为0.5的等值面记录三维空泡演化过程，图13自上而下依次给出了K=0，K=0.5，K=1.0，K=1.5，K=2.0及K=3.0时两发弹丸先后以初速400 m/s垂直入水的空泡形态演化图。

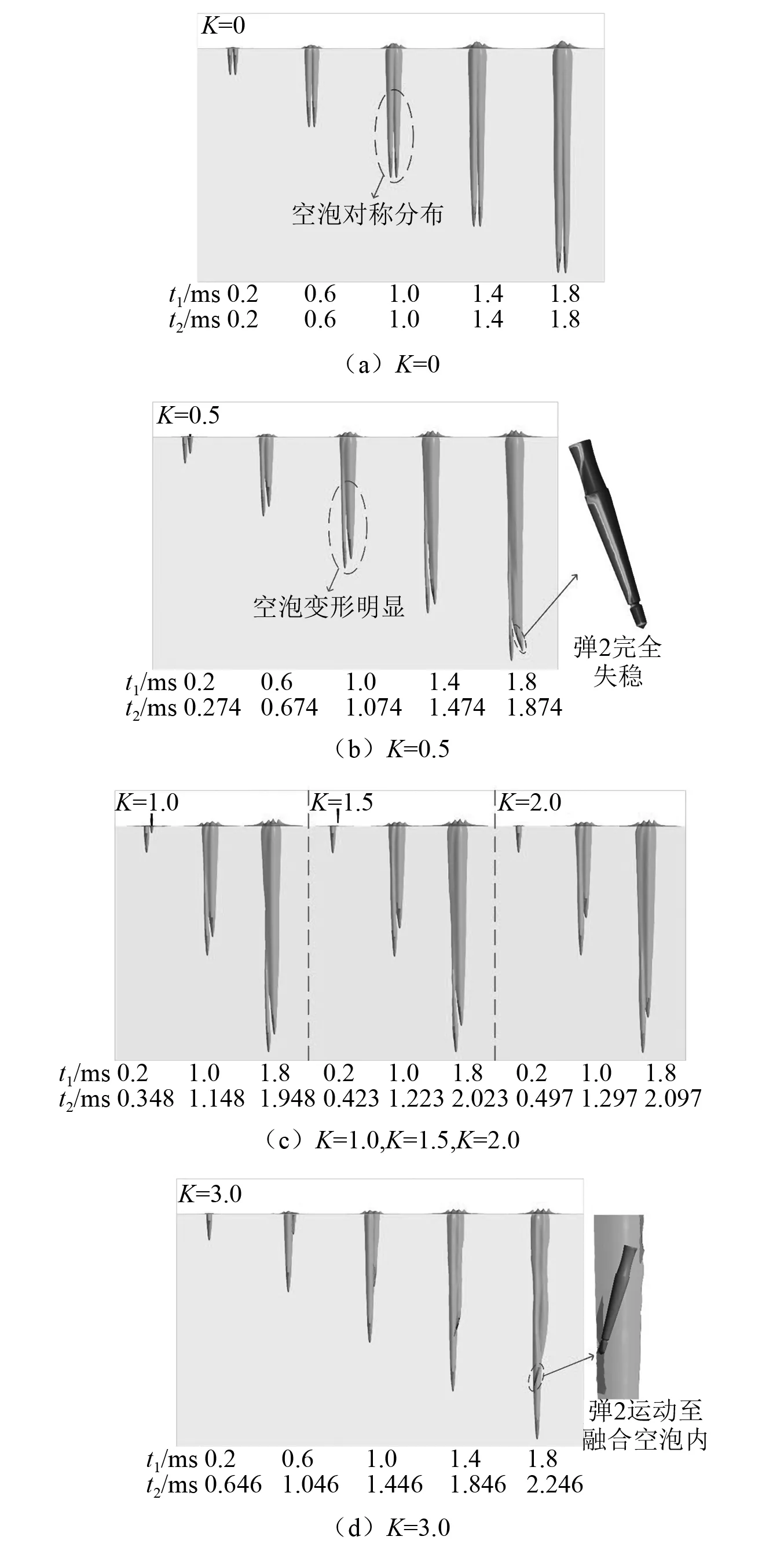
图13 不同初始纵向间距下三维空泡演化过程Fig.13 Evolution process of three-dimensional cavitation at different initial longitudinal spacing

如图13(b)所示，入水初期弹1弹2相继穿过自由液面进入水中并在超空泡的包裹下平稳运动，空泡间的耦合关系与同步并联相比表现出较大的差异。不同于图13(a)中内侧空泡扩张被抑制，两空泡沿轴线呈对称分布的情况，弹2入水后其空泡迅速向左侧膨胀，受其挤压弹1空泡会发生明显的变形，两空泡完全失去对称性。结合图14分析其原因，弹2空泡虽受到弹1周围流体影响，但纵向间距的存在使弹2受到的排斥力低于同步并联工况，同时由于弹2头部存在高压区，而弹1空泡内是由水蒸气及空气构成的低压区，在压力梯度的作用下弹2头部在运动过程中不断挤压弹1右侧空泡，使弹1空泡在右侧产生凹陷。另一方面由于弹2左侧流体流速较快，弹2空泡在向左扩张时所受阻力低于向右扩张，随着弹丸向下运动，弹1空泡被挤压的同时弹2空泡不断向左侧膨胀，最终两空泡在靠近液面处融合。从图13(b)可以看到在运动末期弹2完全失稳，其失稳原因将在后文中进行分析。

图14 异步并联弹丸空泡形态Fig.14 Cavitation of asynchronous parallel projectile

随着弹丸初始纵向间距的增大，由图13(c)可以看出空泡形态变化不大，两发弹丸在水下均保持较为稳定的运动规律。但当K增大到3时，如图13(d)所示弹2入水后的空泡演化及运动规律均发生了较大改变。弹2入水后直接进入弹1的空泡中，弹体周围未能产生独立空泡，畸形的空泡会对弹2的弹道稳定性造成不利影响，弹2在水中逐渐沿顺时针方向发生偏转，运动方向朝向斜下方继续运动。

图15展示了K=0.5时弹1表面水相体积分数的变化规律。从图中可以看出弹1在0.4 ms时出现了沾湿现象，之后沾湿面积先增后减，弹丸发生一次尾拍。观察图13(b)发现，沾湿现象的出现可能与弹2入水后剧烈挤压弹1空泡，使空泡内侧触碰弹1尾部有关。为了进一步研究异步并联时空泡直径变化对弹丸运动的影响，本文分别对弹1和弹2的内侧空泡直径占比进行了测量，测量方法如图16所示，图中Dc代表当前时刻空泡的最大直径，lc为弹尾中点到单侧空泡的距离，测量结果如图17所示。定义无量纲量γ=lc/Dc表示直径占比，当直径占比接近0.5时说明空泡的对称性良好，这有利于弹丸在水下保持较好的稳定性。由图17(a)可以看出，同步并联时弹1空泡的对称性较差，而异步并联工况除K=0.5外，弹1内侧空泡直径占比都在0.5附近，空泡对称性良好，K=0.5时曲线异常的原因将在后文进行详细分析。当K=3.0时由于在0.5 ms后弹2头部进入融合空泡内，弹2空泡不再产生，所以图17(b)中该工况的数据只采集到t2=0.5 ms为止，而其他工况的弹2内侧空泡直径占比都不在0.5附近，其空泡对称性较差。

图15 当K=0.5时弹1表面水相体积分数云图Fig.15 Water phase volume fraction contours of projectile 1 when K=0.5

图16 内侧空泡直径占比测量方法示意图Fig.16 Diagram of inner cavity diameter ratio measurement method

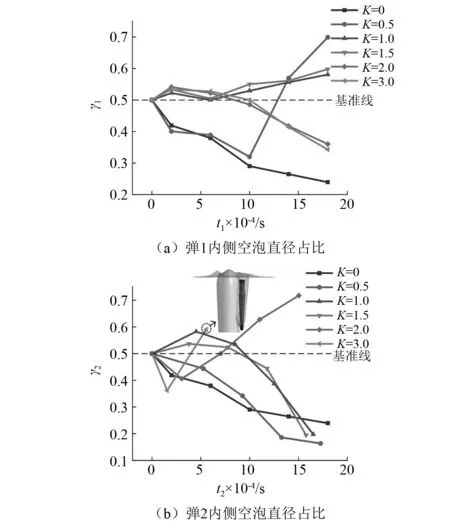
图17 异步并联弹丸内侧空泡直径占比Fig.17 Proportion of diameter of inner cavity of asynchronous parallel projectile

2.2 异步并联入水稳定性分析

图18展示了不同初始纵向间距条件下，弹1高速入水后横向偏移量、横向流体动力系数、偏转角度及横向速度随时间变化的无量纲对比仿真结果，图中：ΔX为弹丸在X轴方向的偏移量，VX为弹丸在X轴方向的速度，CX代表横向流体动力系数，其定义式为

(8)

式中：FX为弹丸在X方向所受流体阻力；ρw为水的密度；v0为弹丸入水的初始速度；A1为弹丸侧截面面积。

由图18(a)可以看出，K=0时弹1运动一段时间后偏移量较大，这是由于弹丸受到了中间流场的强烈干扰，而K=0.5时弹1在运动后期也发生了明显偏移。结合前文分析这与弹1尾部出现沾湿现象有关，沾湿现象的出现一方面是由于弹丸中间流场流速较快，根据伯努利定理这会使两空泡中间流场压力低于空泡外侧，在压差的作用下由图18(c)可知弹1会沿顺时针方向发生偏转。另一方面结合图13(b)可以看出，该工况下两弹丸初始纵向间距较小，在弹2空泡的剧烈挤压下弹1空泡在右侧产生凹陷，空泡与弹尾间的距离减小。如图18(b)所示，沾湿现象的出现使弹1在0.78 ms时横向流体动力系数突然增大，在横向力的作用下弹1不断向左偏移，至1.8 ms后弹丸触碰左侧空泡壁出现二次沾湿,弹丸又受到X轴负方向的阻力。另外由图18(b)还可以看出，弹1在第二次沾湿时受到的X向阻力系数峰值的绝对值大于第一次沾湿，这是由于弹1在第二次沾湿前的偏移过程中积攒了更多的惯性势能，弹丸横向速度相比第一次沾湿时更大，这一点在图18(d)中可以看出。此外，由前文分析可知，异步并联工况除K=0.5外弹1空泡的对称性都较好，从图18中也可以看出除K=0.5工况外其余异步并联工况弹1均能平稳运动，这验证了良好的空泡对称性有利于弹1在水下平稳运动。

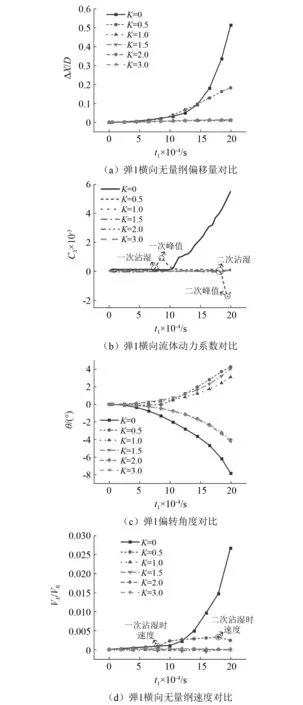
图18 初始纵向间距对弹1稳定性的影响Fig.18 Influence of initial longitudinal spacing on the stability of projectile 1

相比起弹1，弹2入水时面临的初始流场更为复杂，在弹1空泡流场的影响下弹2的入水运动特性变化明显。图19给出了弹2在水下运动过程中横向无量纲偏移量、横向流体动力系数、偏转角度及横向无量纲速度随时间变化情况。由图19(a)可以看出，K=0，K=1.0，K=1.5及K=2.0时弹2的偏移量都很小，而K=0.5和K=3.0时弹2均发生严重的失稳。以下分别对这两个工况弹2失稳的原因展开分析。

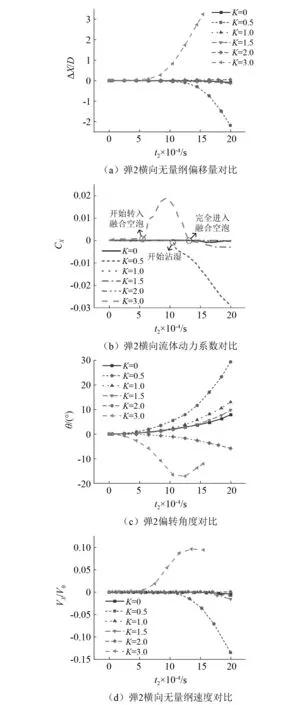
图19 初始纵向间距对弹2稳定性的影响Fig.19 Influence of initial longitudinal spacing on the stability of projectile 2

从图19(c)可以看出，K=0.5时弹2在入水初期便较为不稳定，弹丸沿逆时针方向偏转角度相比其他工况较大。这是由于弹2入水时受到了弹1排开流体的影响，考虑到该工况两发弹丸入水时间差较小，弹1入水排开的流体在弹2附近具有较大的动能，此流体动能传递到弹2头部形成偏转力矩使弹2偏转角增大，受力关系如图20所示。

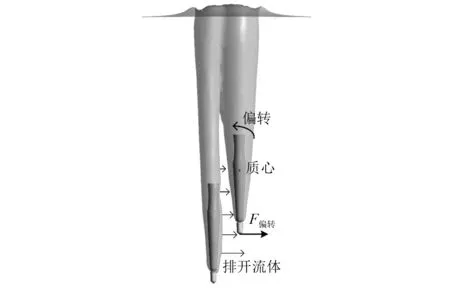
图20 当K=0.5时弹2受力关系Fig.20 Stress relationship of projectile 2 when K=0.5

同时结合图17(b)可以看出，相比其他异步并联工况，K=0.5时弹2周围空泡对称性较差，不对称的空泡分布使弹2受到了不对称的流体动力，在不对称流体动力的作用下弹2不断向左偏转，并在t2=1 ms时弹2尾部左侧沾水，弹丸受力陡增如图19(b)所示。之后由于弹尾沾湿提供的回转力不足以让弹丸的偏转角速度减小为零，弹2在水中继续偏转并最终倾覆。

由图13(d)可以看出，K=3.0时弹2入水后空泡不能正常产生，相似于K=0.5时弹丸会受到不对称的流体动力。同时由图19(b)可知，弹2在0～0.59 ms内横向流体动力系数在5×10-4左右，而其余工况仅为5×10-5，这说明该工况在入水前期所受横向力较大。在横向力的作用下弹2偏移量逐渐增大，到t2=0.59 ms弹丸头部开始进入融合空泡内而弹身及弹尾刺破空泡进入水中，失去完整的空泡包裹导致弹丸横向受力陡增，之后经历在融合空泡内短暂的运动后，弹2穿透空泡左壁进入水中完全失稳。

2.3 异步并联入水减阻特性分析

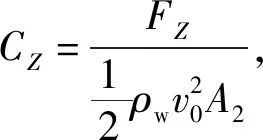
从图21可以看出，在入水瞬间弹丸纵向阻力系数陡增，弹1在入水瞬间受到剧烈的冲击载荷作用。在入水后随着弹丸速度的逐渐衰减以及高速弹丸在水下运动时产生了能完整包裹自身的超空泡，弹丸纵向阻力系数骤降后缓慢衰减。观察图21发现K=0时弹1在t1=1.03 ms后纵向阻力系数逐渐升高，这是由于在该时刻弹1发生偏转，尾部右侧出现沾湿现象。当K=0.5时弹1在0.78 ms纵向阻力系数发生了一次波动，这对应于前文所述的弹1在空泡壁被挤压后发生第一次沾湿，而t1=1.8 ms时纵向阻力系数逐渐升高对应于弹1向左偏移后发生二次沾湿，这三个时刻弹1表面水相体积分数云图如图22所示。

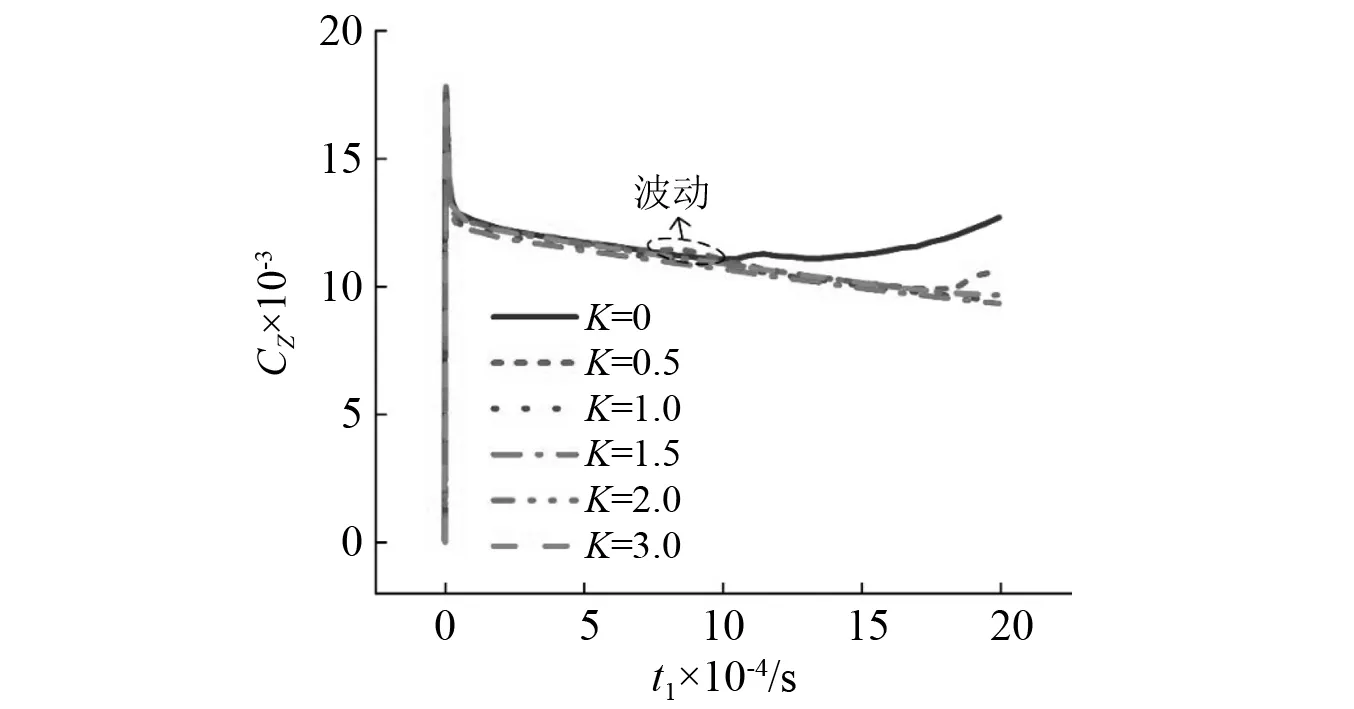
图21 弹1纵向阻力系数对比Fig.21 Comparison of longitudinal drag coefficients of projectile 1

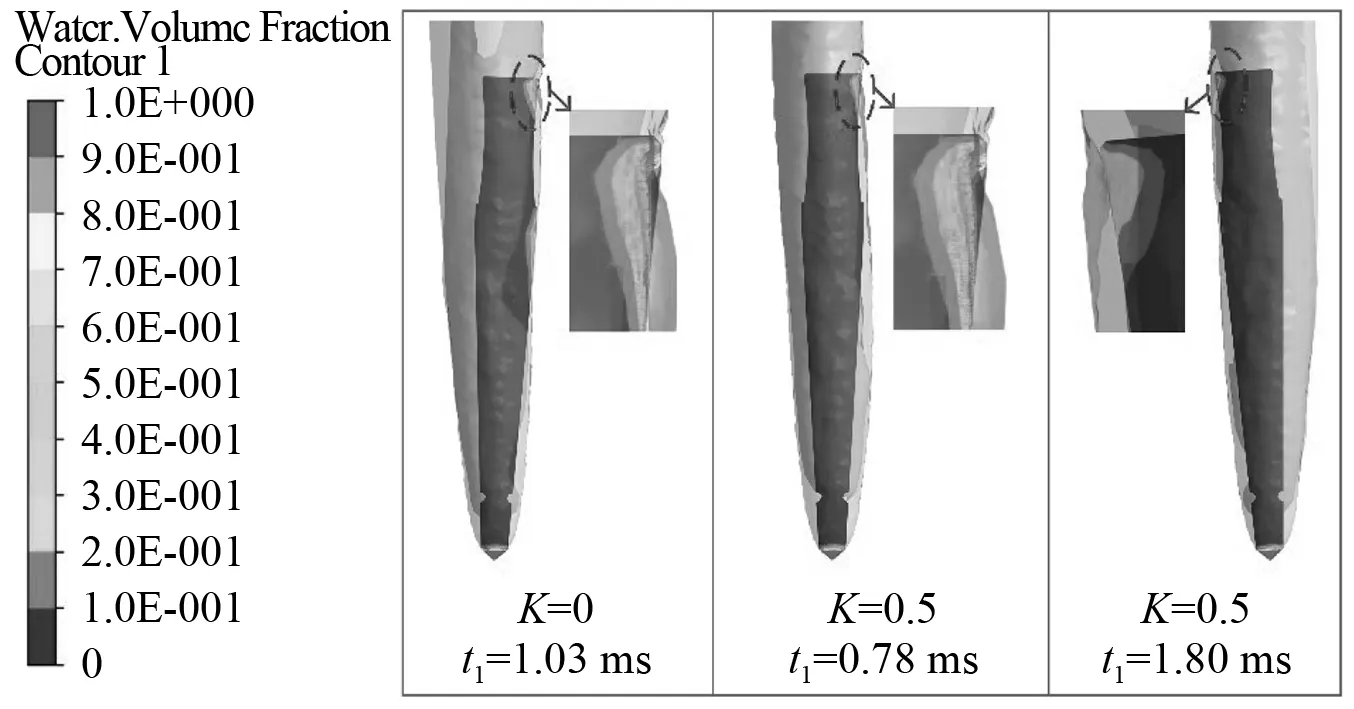
图22 弹1表面水相体积分数Fig.22 Water volume fraction of projectile 1

图23反映了在不同初始纵向间距下弹2所受纵向阻力系数随时间变化规律。由图23可以发现，纵向间距的存在使弹2入水时受到的冲击载荷峰值明显降低，同时随着初始纵向间距的增大，冲击载荷呈现递减趋势，究其原因在于初始纵向间距的存在使两发弹丸入水时间存在时间差。弹1入水后在排开周围流体的同时不断将动能传递给周围，到弹2入水时其初始流场已不是静止水面，压力的减小使弹丸入水时纵向受力降低，另外随着初始纵向间距的增大，弹1空泡逐渐扩张充分，至K=3时弹2入水后便进入弹1空泡内，弹丸所受纵向阻力系数较小。观察曲线，当K=0.5时纵向阻力系数在t2=1.03 ms后增大，结合前文分析这是由于在t2=1.03 ms时弹2尾部左侧出现沾湿现象，而K=3.0时阻力系数曲线出现了两次增大。其中第一次增大发生在t2=0.59 ms，弹丸在偏转力的作用下转入水中，之后随着弹丸速度的衰减以及回转力的增大纵向阻力曲线出现波动，至弹丸完全进入融合空泡后由于运动阻力很小纵向阻力系数减小。第二次增大发生在t2=1.3 ms，偏转弹丸刺破融合空泡左壁进入水中，剧增的纵向阻力让弹2在水下完全失稳。这三个时刻弹2表面水相体积分数云图如图24所示。

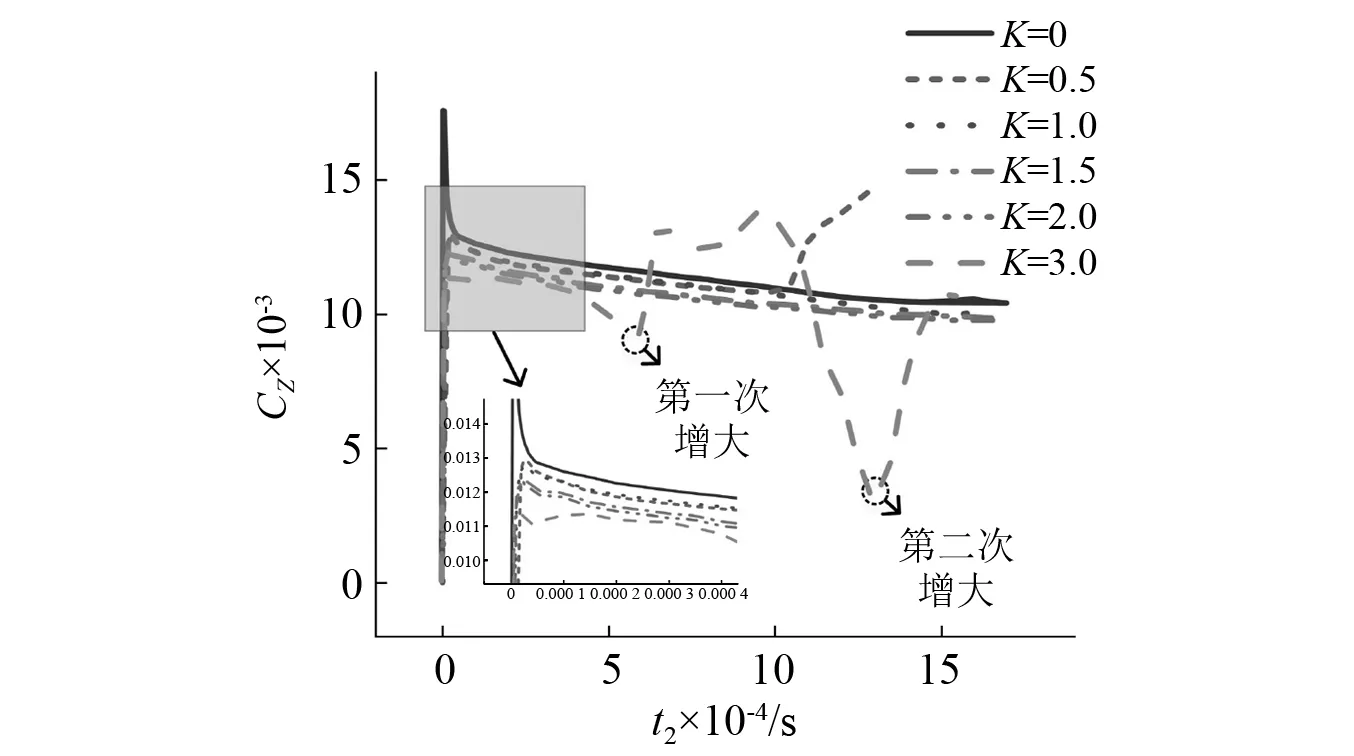
图23 弹2纵向阻力系数对比Fig.23 Comparison of longitudinal drag coefficients of projectile 2

图24 弹2表面水相体积分数Fig.24 Water volume fraction of projectile 2

3 结 论

本文以异步并联超空泡射弹入水问题为探究对象，运用数值模拟的方法分别对不同工况下两发弹丸的流场特性、稳定性及减阻特性进行了对比分析，研究了异步并联射弹初始纵向间距的变化对弹丸运动特性的影响规律，主要得到了以下结论：

(1)异步并联超空泡射弹入水产生的空泡形态与同步并联相比变化明显。具体表现为弹1空泡在压差作用的影响下在空泡右侧产生凹陷，而弹2入水后由于左侧流体流速较快，其空泡会向左侧加速膨胀，在这两个因素的影响下弹1、弹2的空泡融合为一并逐渐拉长。

(2)异步并联超空泡射弹初始纵向间距对并联射弹运动稳定性影响明显。K=0.5时，由于空泡受到剧烈挤压弹1尾部发生一次尾拍而弹2出现严重失稳，其余工况随着初始纵向间距的增加，弹2基本不对弹1造成影响，弹1周围空泡的对称轴良好。K=3.0时，弹2入水后受弹1空泡的强烈干扰发生大幅偏转，之后经历在弹1空泡内的短暂运动后进入水中完全失稳。而其余工况随着初始纵向间距的增加，弹丸的偏转角呈现递减趋势，除K=0.5外弹2均表现出较好的稳定性。

(3)异步并联超空泡射弹初始纵向间距对并联射弹减阻特性影响明显。相比起同步并联，异步并联时弹2受到的冲击载荷峰值明显减小，并且随着初始纵向间距由0增大到3.0倍弹长，弹2受到的入水冲击载荷逐渐降低。