钢箱梁受弯屈曲的磁记忆参数表征

韦璐茜，苏三庆，王 威，严敏嘉

(1.广西民族大学 建筑工程学院，南宁 530006;2.西安建筑科技大学 土木工程学院，西安 710055)

波纹腹板箱型桥梁由于加工制作相对简单、稳定性强、弯剪承载力高而得以广泛应用于桥梁领域[1]。钢箱梁在服役期间存在很多隐患，其中由于构件屈曲造成的结构性破坏将对人类的生命财产安全产生严重的影响。历史上曾多次出现由于局部失稳而导致的工程事故。如1970年，澳大利亚墨尔本附近的Westgate桥在施工时，跨中的上翼板出现失稳，导致112 m的整跨倒塌；Kohakob A.h.和Mzxob A.H.曾分析前苏联在1951年—1977年期间所发生的59起重大的钢结构事故，其中29%是属于结构的整体失稳或局部失稳。从1969年11月—1971年11月不到两年的时间内,在欧洲就有4座正在施工中的正交异性桥面板桥发生坠梁事故[2]。

针对施工中桥梁钢结构的失稳，若能从桥梁的监测结果实现钢结构的失稳的早期识别和预报，则可以及时发现存在的安全隐患，避免灾难的发生。因此，对在役钢结构的失稳监测十分有必要。

现有的失稳监测技术主要包括：振动监测复合材料圆柱壳失稳荷载；利用应变和沉降传感器进行稳定监测；利用热辐射红外线监测；通过能够传感结构失稳先兆的装置进行监测等等[3]。但上述监测方法存在着以下问题：①需要预知易失稳部位才能保证监测精度；②监控参数易受到随机信号及噪声的影响；③参数测量困难等。

金属磁记忆检测技术是一种新兴的无损检测技术，克服了传统检测技术成本高、操作耗时的缺点[4]，可用于铁磁构件的早期损伤检测[5]。该检测技术搭建了力和磁场间的桥梁，通过对磁场强度的测量可得知试件的受力情况。其易操作、可反映受力情况的特点使得运用该技术进行构件的屈曲监测成为可能。

金属磁记忆检测技术的主要检测机理较为复杂。无外物理场作用时，铁磁材料内部的磁畴和磁畴壁无规律，宏观上不显示磁性。在应力场和地磁场的共同作用下，铁磁材料内部产生磁畴壁的转动和磁畴的定向移动，宏观上对外显示磁性。受力后构件的磁化状态“记忆”着应力集中位置和缺陷位置。

其经典的判别特征如图1所示，试件宏观缺陷位置的磁场强度法向分量Hp(y)(后文称作法向磁信号)具有改变符号且过零点的特点，并在两侧分别产生波峰和波谷[6]。

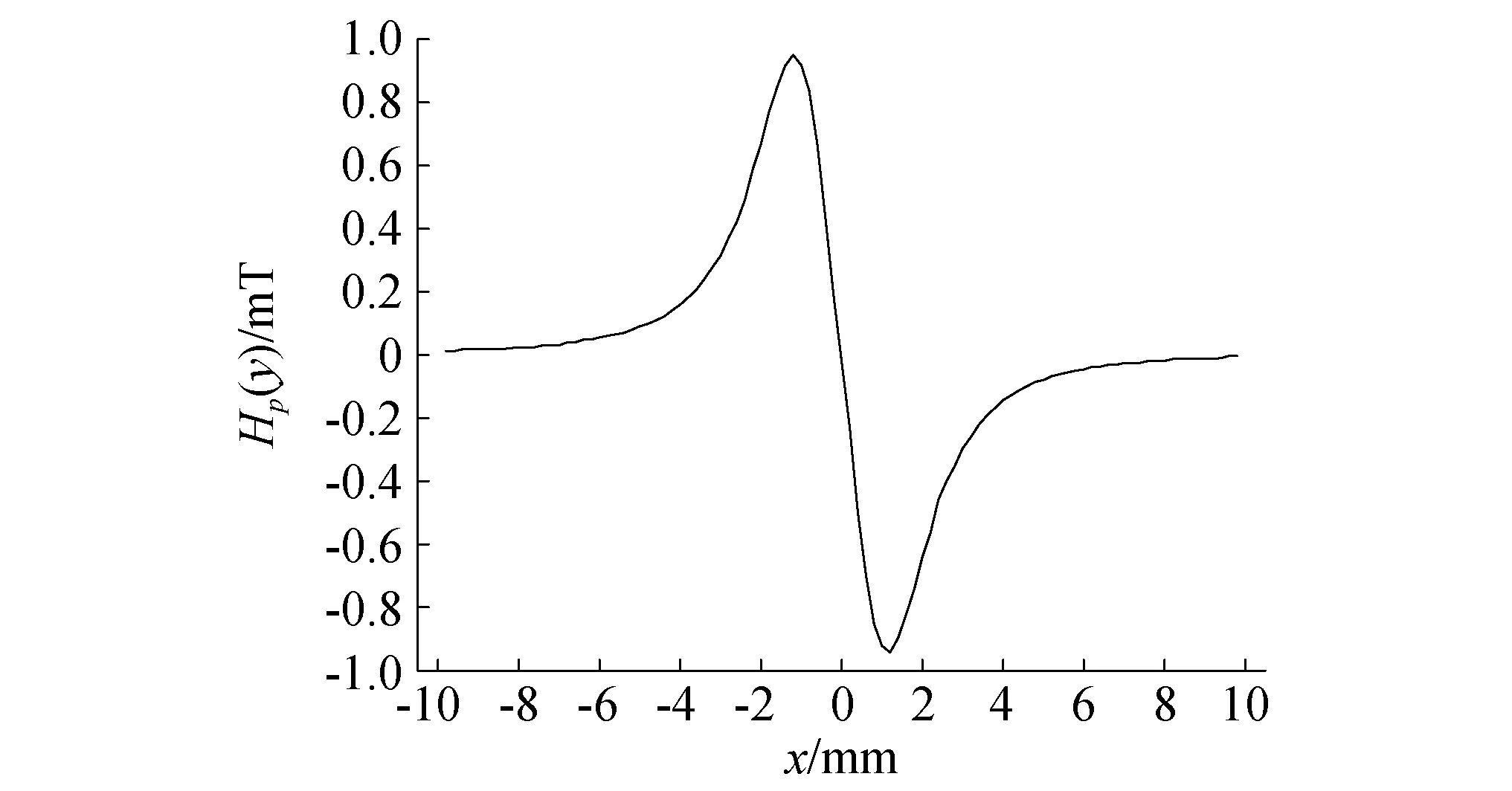
图1 磁场法向分量分布曲线Fig.1 Distribution curve of the normal component of magnetic field

对于磁记忆技术的工程应用，学者们从不同方面进行了研究。张军等[7]采用封闭的法向相轨迹和法向梯度大小区分高铁轮对的受力状态；杨茂等[8]运用磁记忆检测技术定位混凝土内部钢筋的锈蚀区域。磁记忆检测技术目前已应用于输油管道[9]、无缝钢轨[10]、钢丝绳[11]等领域的损伤检测中。在磁记忆检测的损伤评判参数方面，学者们进行了大量的研究。胡先龙等[12]发现磁场梯度K随着应力集中因子的增大而增大，因此采用K表征铁磁材料表面的应力集中程度；Huang等[13]采用法向磁信号梯度最大值Kmax与平均磁信号梯度值Kstd的比值定量描述应力集中程度。王威等[14-16]也从磁信号梯度的角度提出不同的损伤评判参数。

上述研究仅适用于试件产生宏观缺陷的情况，而对于钢构件屈曲的情况尚未考虑。为了进一步研究磁记忆检测技术对于失稳监测的可行性，本文进行了波纹腹板钢箱梁四点受弯试验，采集上翼缘的法向磁信号Hp(y)，提取磁特征量，研究构件中的屈曲位置的判别方法。

1 试验方案设计

1.1 试件设计

本试验拟对波纹腹板钢箱梁进行静力测试，构件三维图如图2所示。

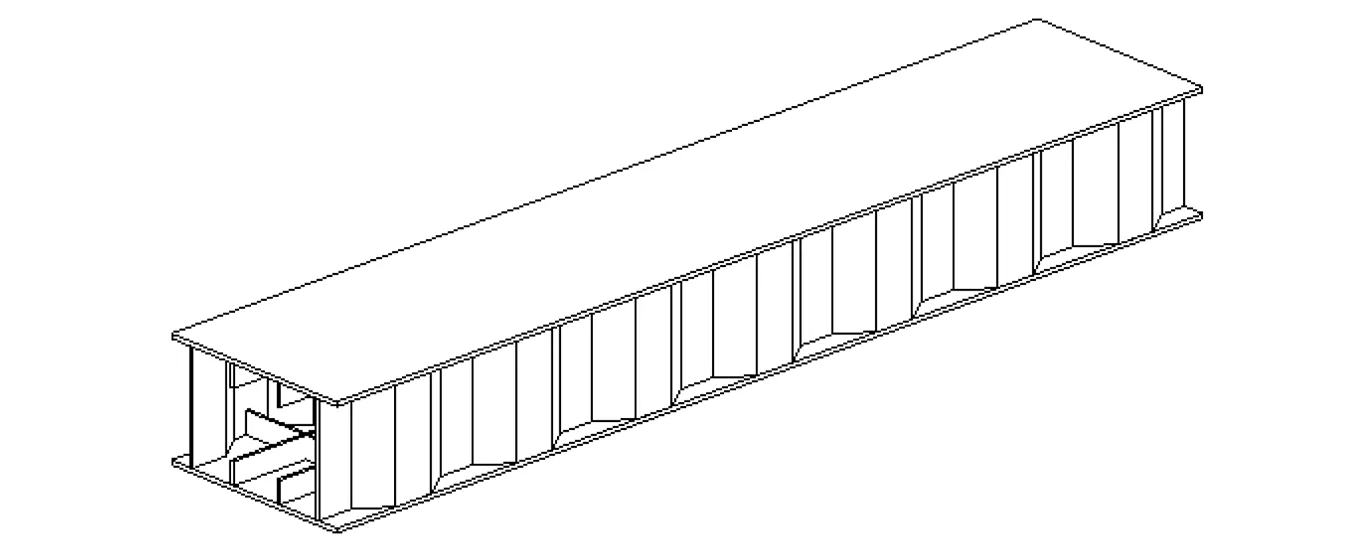
图2 构件三维图Fig.2 Three dimensional diagram of component

波纹腹板钢箱梁的腹板厚度为6 mm，上、下翼缘的厚度是8 mm。本试验根据《组合折腹板桥梁设计模式指南》和JTG D64—2015《公路钢结构桥梁设计规范》选用波纹腹板为1/4缩尺的1000型梯形波纹板作为试验梁的腹板，波纹腹板尺寸如图3所示。波纹腹板钢箱梁的截面尺寸如图4所示。

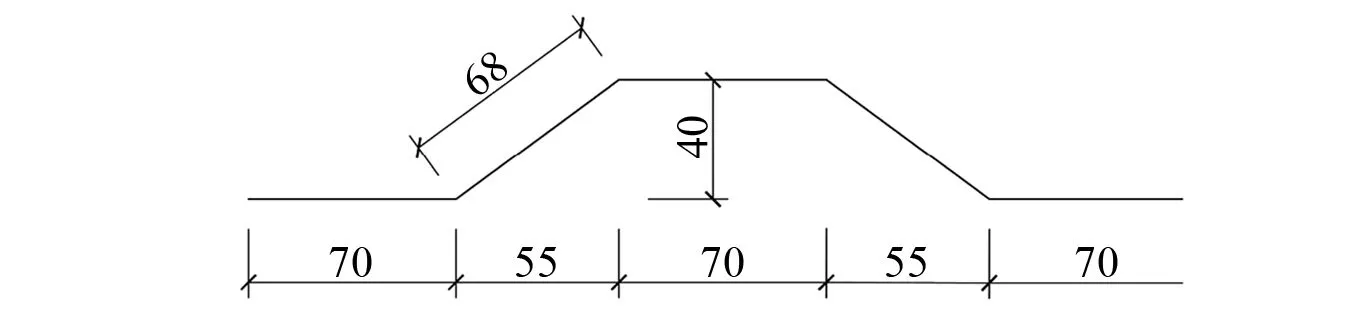
图3 波纹腹板尺寸(mm)Fig.3 Dimensions of corrugated web (mm)

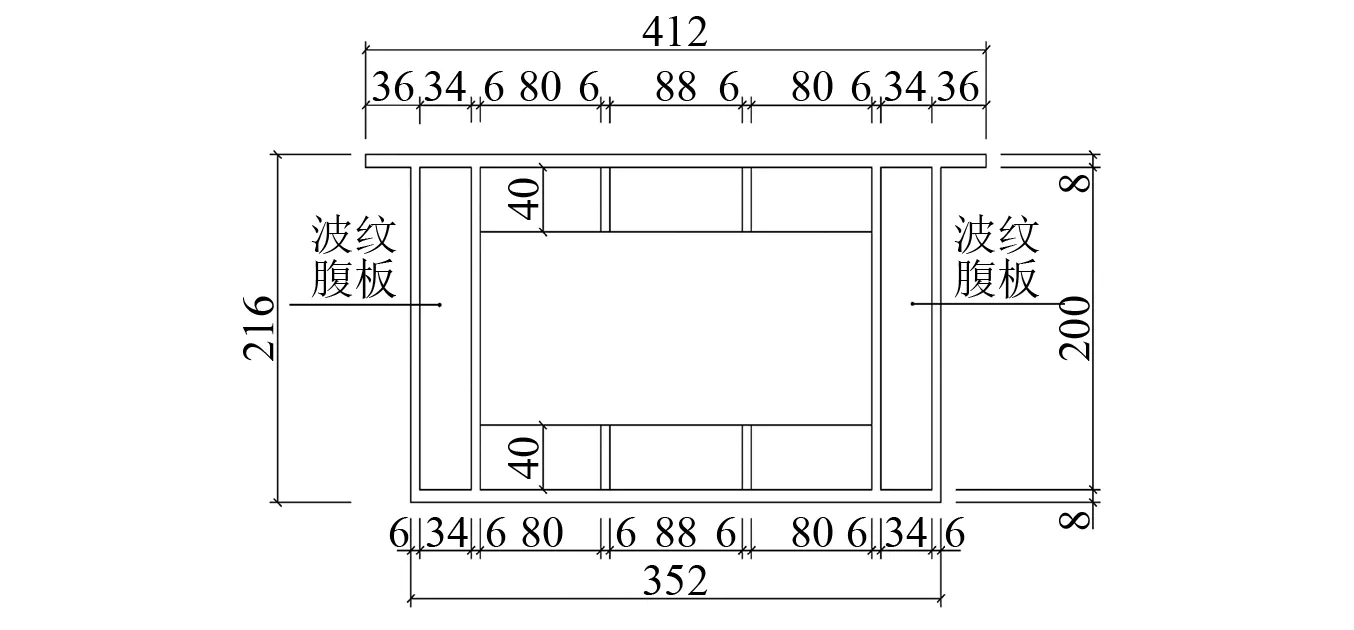
图4 波纹腹板钢箱梁截面尺寸(mm)Fig.4 Section size of steel box girder with corrugated web (mm)

1.2 试验材料

本试验采用Q345qC钢作为构件材料。根据《金属材料拉伸试验第1部分：室温试验方法》中对材性试验试件设计的相关要求，制作用于拉伸试验的钢板件，并分别进行了厚度为6 mm和厚度为8 mm的标准板件的拉伸试验以得到材料性能的表征数据，总结如表1所示。标准试件尺寸图如图5所示。

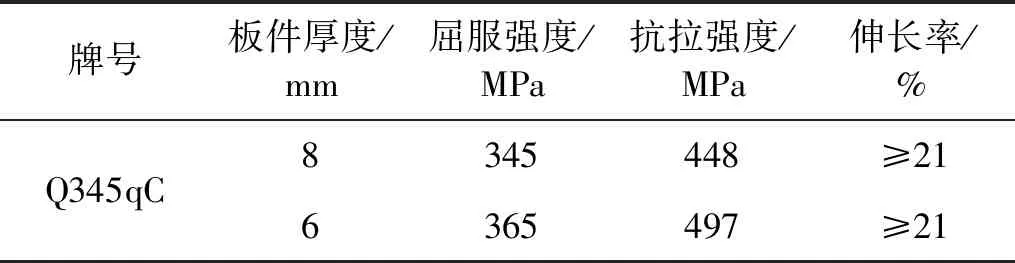
表1 Q345qC钢的物理性能Tab.1 Physical properties of Q345qC steel

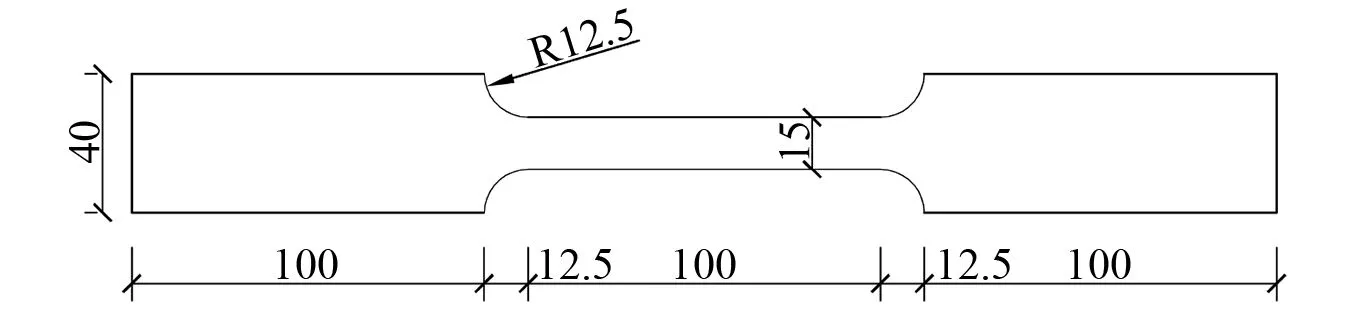
图5 标准拉伸试件尺寸(mm)Fig.5 Dimensions of standard tensile specimens (mm)

表2显示了试件材料的化学成分。为了保证试验梁的局部稳定性，在试件的上、下翼缘设置了横向和纵向的加劲肋，所用材料与翼缘、腹板相同。

表2 Q345qC钢的化学成分表Tab.2 Chemical composition of Q345qC steel

1.3 检测线布置及量测方法

如图6所示，在试件上翼缘布置了一条检测线u1，用于采集试件表面的法向磁信号，每条检测线间以及每个检测点间的距离为50 mm。本试验采用的应变片型号为BX120-3AA，主要的技术参数为：阻值为120 Ω±1%、有效尺寸为3 mm×2 mm、灵敏系数为2.00。设梁长方向为x轴方向。

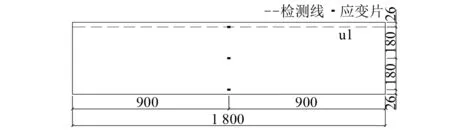
图6 波纹腹板钢箱梁截面尺寸及检测线布置(mm)Fig.6 Test line and strain gauge layout (mm)

本试验采用分配构件将所加荷载分配到试件的三分点处，试验梁的加载点位置以及位移计的放置位置如图7所示，位移计放置在试件下翼缘跨中位置，记录每级荷载下的变形量。

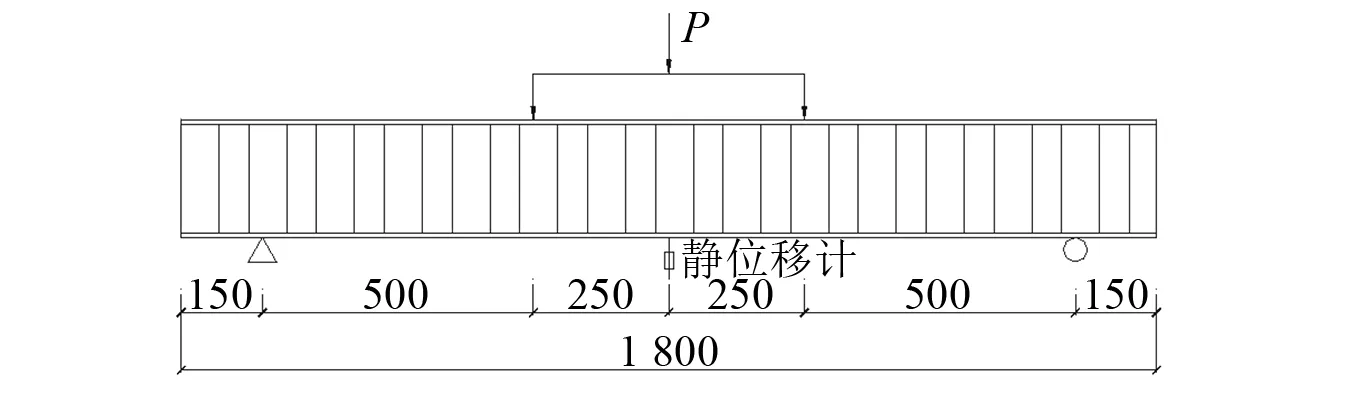
图7 加载及位移计布置图(mm)Fig.7 Layout of loading and displacement meter(mm)

试验使用EMS-2003智能磁记忆/涡流检测仪采集试件表面的法向磁信号Hp(y)。EMS-2003智能磁记忆检测仪的主要技术参数如表3所示。

将检测仪的显示模式调为数字显示模式，探头采用双通道笔式探头。使用前，为了抑制地磁场强度以获取真实的磁场强度法向分量值，将仪器按照仪器探头上的传感器1为标准进行校准，并将背景磁场抑制选为“-CH1”。

为了减小试验偶然误差，采取了以下措施：每个检测点采集三次法向磁信号值，放弃相差很大的信号，取剩下信号值的的平均值作为该检测点的试验检测值。此外，在检测下一条检测线之前，需要对检测仪进行归一，即重新校准。由于磁场强度值容易受到探头与试件检测表面的角度以及探头的提离高度的影响，因此为了减小人工测量误差，在检测时统一尽量使探头与试件表面垂直，并将探头轻贴在试件表面。

1.4 加载方案

加载设备采用YAJ20000电液伺服压剪试验机，如图8所示。试件采用分级加载的制度，每200 kN停机保载并对试件表面的法向磁信号进行检测，当加载到试件的承载能力下降到其极限承载力的85%时停止加载。

图8 试验加载机器Fig.8 The experiment machine

2 试验结果及分析

2.1 试验过程及破坏形态

图9显示了钢箱梁的荷载-位移曲线。结合两种作图法[17]近似确定屈服荷载，得到钢箱梁的屈服荷载大致为900 kN，极限荷载为1 050 kN。钢箱梁的破坏形态如图10所示。破坏类型属于弯曲破坏，产生了弯曲变形并出现了上翼缘的局部受压屈曲，并未产生肉眼可见的宏观裂缝或其他缺陷。

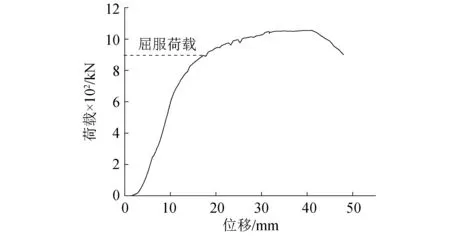
图9 梁的荷载-位移曲线Fig.9 Load-displacement curve of the beam

图10 试件破坏形态Fig.10 Failure pattern of the specimen

2.2 应力分布模拟分析

为了解箱梁的应力集中位置，本文选用ABAQUS软件而来模拟应力分布，采用C3D8R单元建模，并采用沙漏控制。荷载的施加采用静力加载方式进行，并选用点-面耦合的方式施加荷载。

为了验证有限元模拟结果的正确性，采用对比的方式，将模拟试件的破坏形态和跨中位移同试验试件进行对比。ABAQUS中施加的荷载为960 kN，模拟得到的下翼缘跨中挠度为12.28 mm(如图11所示)，试验试件下翼缘通过位移计的测量得到的跨中位移为11.06 mm，模拟结果和试验结果的误差为11.0%，在15%的误差范围内。

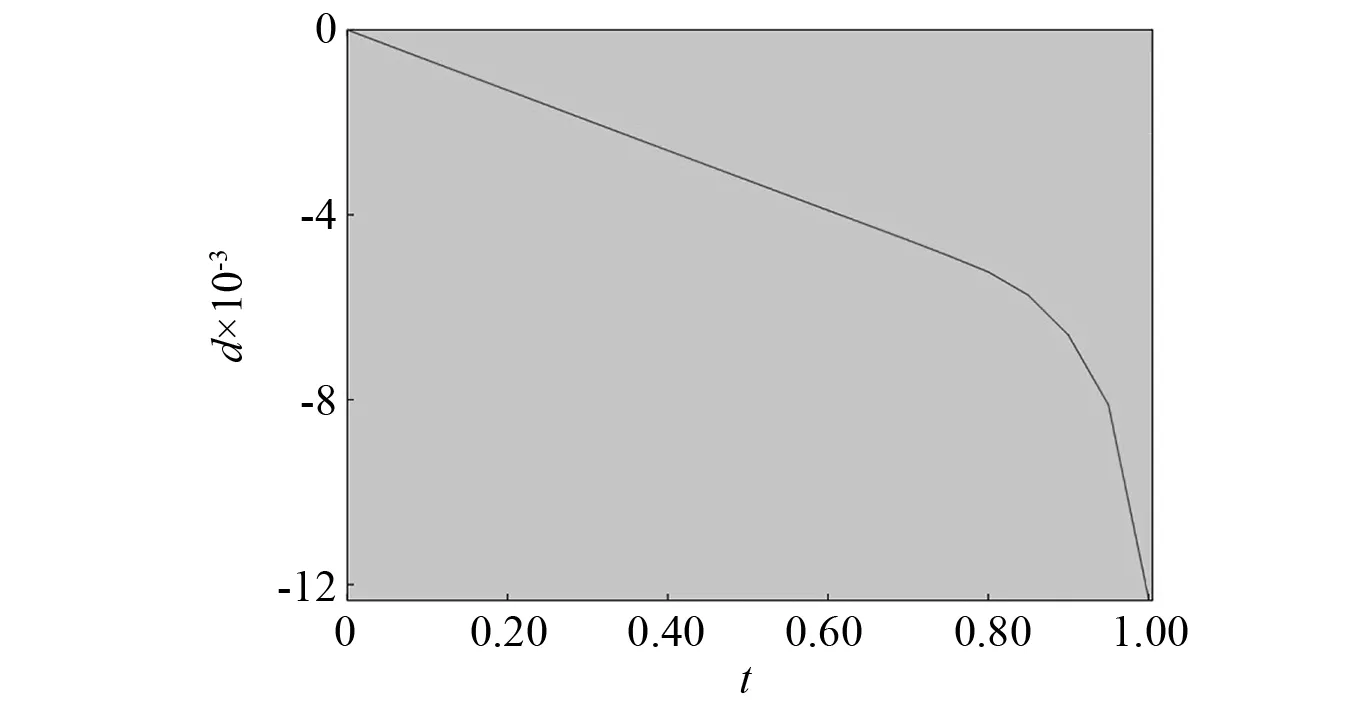
图11 下翼缘跨中挠度随时间变化曲线Fig.11 The curve of mid-span deflection over time on the lower flange

模拟试件的破坏形态和试验试件相似。通过比对跨中挠度和破坏形态，可认为有限元模型对于波纹腹板钢箱梁的受力性能模拟结果的可靠度较高。

在ABAQUS工具中选取场输出中的正应力S11云图，得到直腹钢箱梁的正应力都分布在翼缘，而切应力都分布在腹板的结论，正应力分布云图如图12所示。

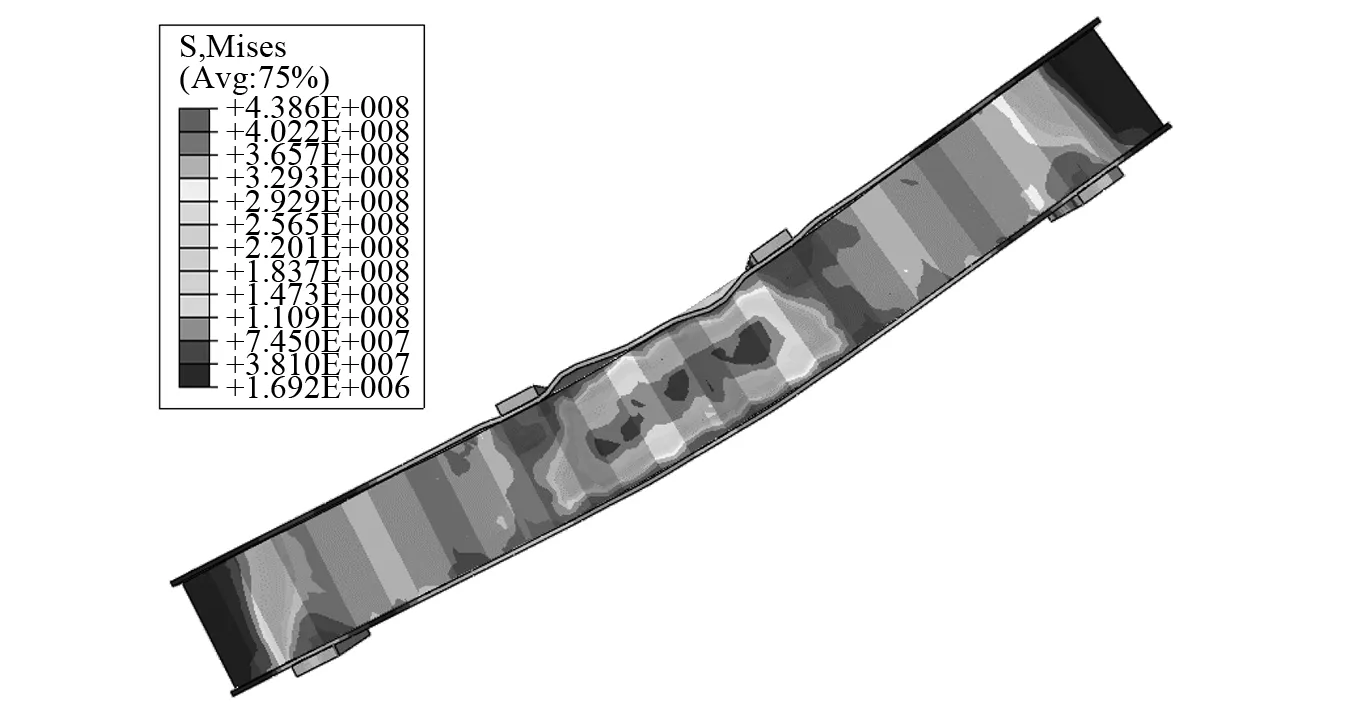
图12 模拟试件的破坏形态Fig.12 Normal stress profile

提取上翼缘的正应力分布曲线，如图13所示。可以看出在上翼缘的纯弯段存在三处应力集中，分别为x=600～700 mm，x=850～950 mm，x=1 100～1 200 mm处。

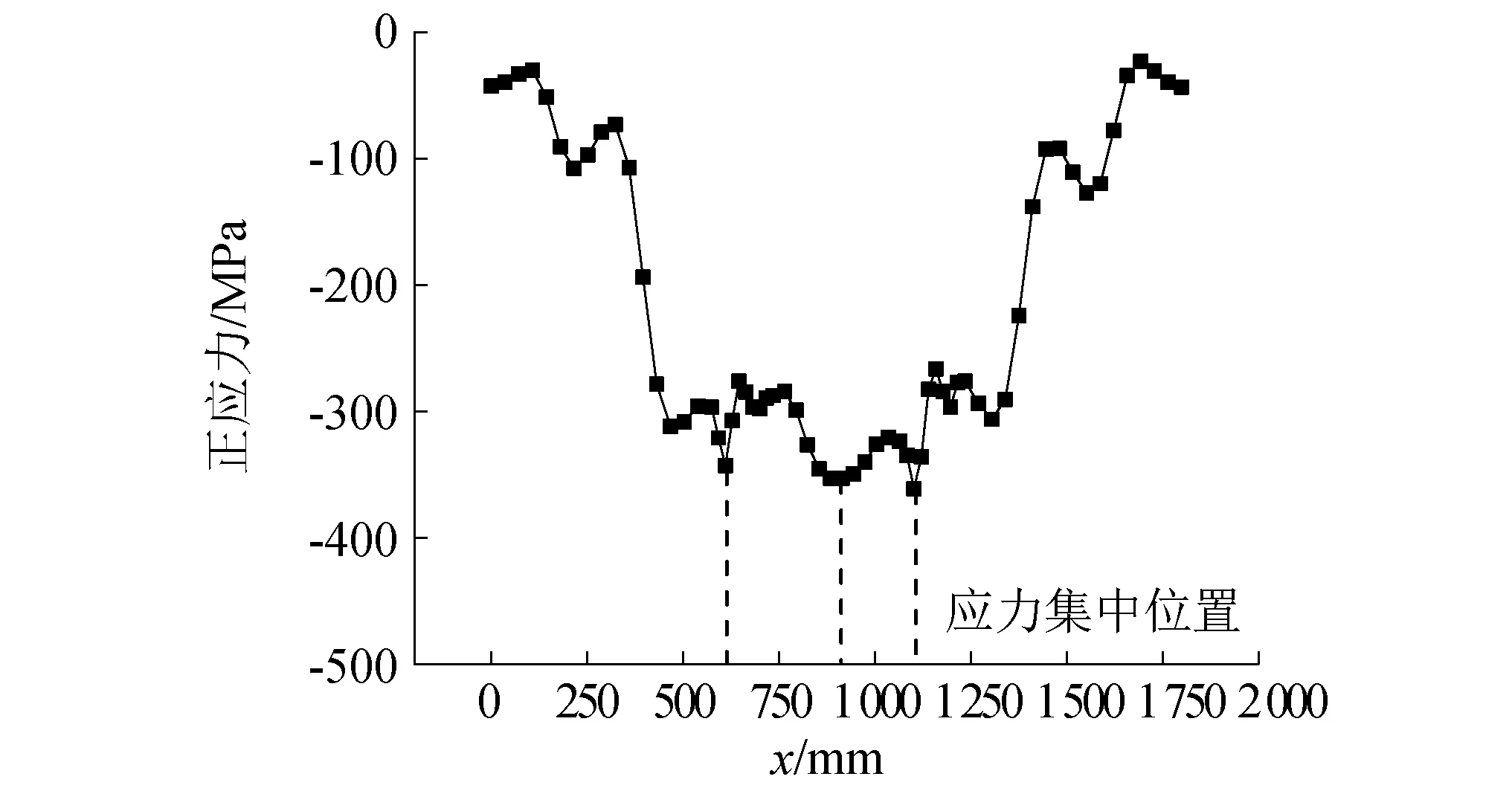
图13 上翼缘的正应力分布Fig.13 The normal stress distribution of the upper flange

3 屈曲磁表征量分析

由于试件未退磁，初始磁信号不具有规律性，且试件未出现明显裂纹，因此用常规的法向磁信号过零点的方法无法判别屈曲位置，检测到的法向磁信号变化无明显规律。

为了探究判别易屈曲位置的方法，提取磁特征量|ΔHp(y)|，该特征量可采用荷载等级为ikN时的法向磁信号值减去初始法向磁信号值再取其差值的绝对值得到，用公式表达为

|ΔHp(y)|=|Hp(y)Fi-Hp(y)F0|

(1)

式中：Fi为荷载等级为ikN；F0为荷载等级为零。

磁特征量|ΔHp(y)|可以反映应力大小，即应力较大区域的法向磁信号变化较大。根据此特点，引入屈曲磁表征量Hcon，表示为

(2)

式中：|ΔHp(y)|为检测点p的法向磁信号变化量，具体计算公式见式(1)；|ΔHp(y)|ave为沿检测线方向所有检测点的|ΔHp(y)|平均值。

3.1 屈曲位置判别方法

选取试件上翼缘的检测点，绘制检测点的磁特征量Hcon随荷载变化的曲线进行分析。两侧弯剪段上每隔100 mm选取一个检测点，纯弯段上选取所有检测点进行分析。不同检测点的Hcon值随荷载变化的规律，如图14所示。

从图14(a)中可以看出，剪切段的检测点变化较为平缓，且没有明显的规律性，图14(b)中有五个检测点变化较为明显且具有一定规律性，分别是x=650 mm，x=850 mm，x=950 mm，x=1 050 mm，x=1 100 mm。

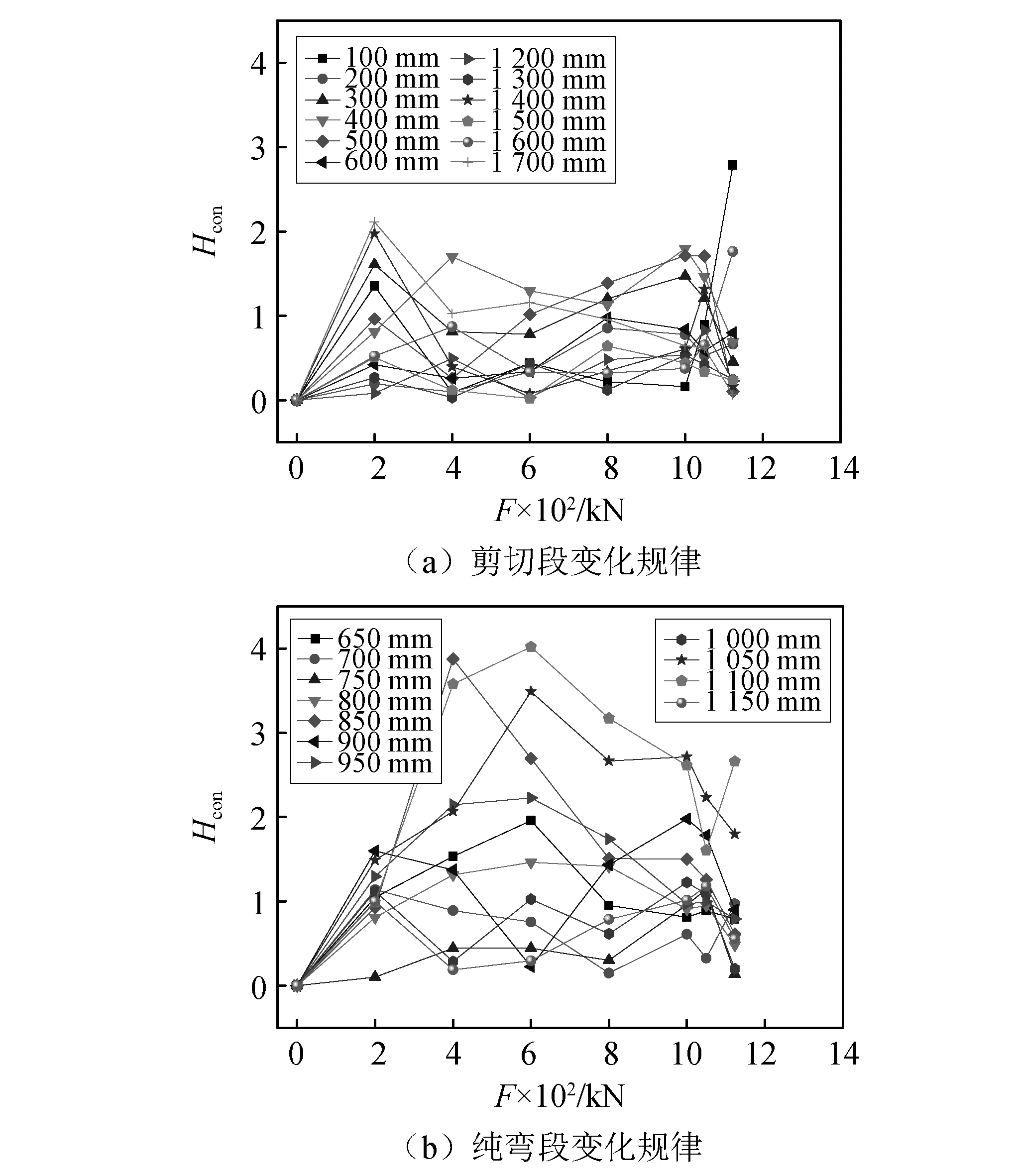
图14 Hcon随荷载的变化曲线Fig.14 The curve of Hcon change with load

选取其中三个位置，即x=650 mm，x=950 mm，x=1 100 mm三处位置分析Hcon随荷载的变化规律，如图15所示。

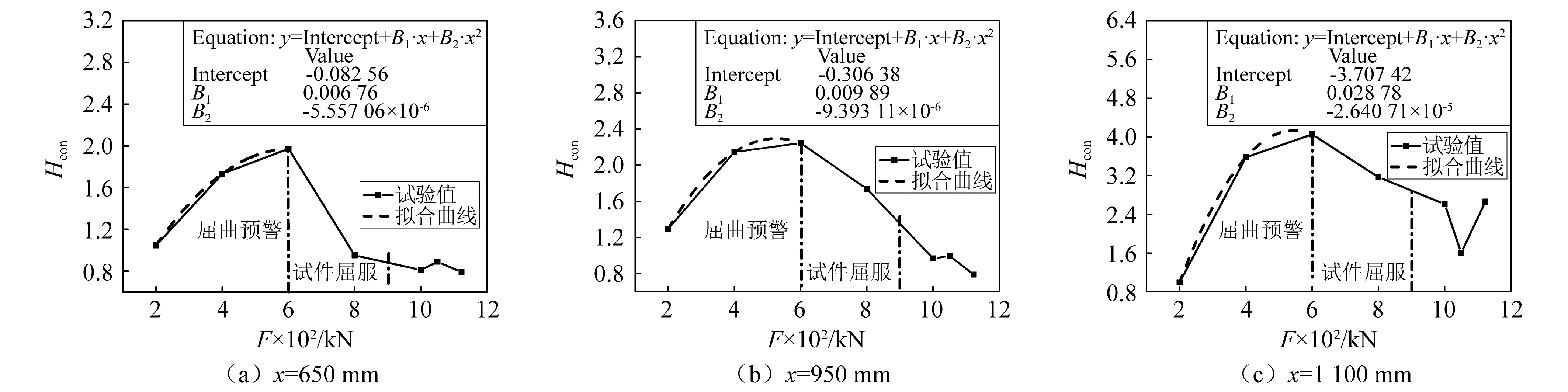
图15 屈曲位置的Hcon随荷载变化规律Fig.15 Change law of Hcon with load at stress concentration position

三个位置处的Hcon随着荷载的增大都呈现出弹性阶段增大，临近试件屈服时发生明显的下降的规律。

将这三个位置与图13中的应力分布图进行比较，可以发现，具有明显变化规律的检测点位置与应力集中位置有较高吻合度。再对照图10和图12的破坏形态，构件在x=850～950 mm范围内发生局部屈曲，该特征与具有明显变化规律的检测点位置，以及应力集中位置都能相互对应。因此，初步判断，通过检测点规律的变化可以判断屈曲位置，同时进行以屈曲预警。

3.2 屈曲位置变化规律理论分析

磁表征量Hcon随荷载的变化规律可以用法向磁信号的变化规律来解释。

3.2.1 上升阶段理论分析

弹性阶段法向磁信号的上升可以运用修正的Jiles-Atherton模型[18]解释，修正模型适用于四点受弯工字梁的纯弯段，同时也适用于本试验试件的纯弯段。试件的内部磁场有效场可以表示为

Heff=bσ2+aσ+H+αM

(3)

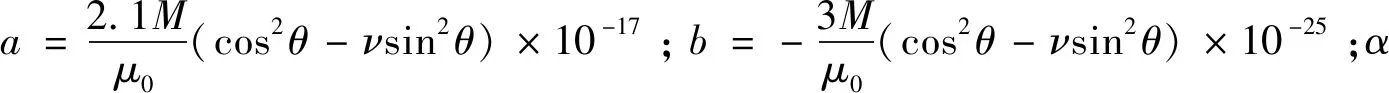
根据材料磁化的基本理论[20]，铁磁材料的磁化强度与外加磁场强度之间的关系满足

M=χmH

(4)

式中，χm为磁化率，χm=μσ-1。因此，式(4)又可表示为

M=(μσ-1)H

(5)

在铁磁材料被磁化后，由于材料的磁化引起的磁场强度改变量为Hp，等同于磁化强度M。因此，当外加磁场为环境磁场并保持不变时，法向磁信号和环境磁场强度之间的关系可以表示为

Hp(y)=(μσ-1)H(y)

(6)

式中：μσ为材料在应力作用下的相对磁导率；H(y)为环境磁场强度。在本试验中，试件所处环境磁场为地磁场，且试件所处位置保持不变，因此环境磁场强度H(y)可视为常数。因此，H(y)的大小值随着应力作用下的相对磁导率的变化规律而变化。

文献[21]提到，在弹性阶段

(7)

式中：μσ为应力作用下的相对磁导率；μ0=4π×10-7H/m为真空磁导率；μ为初始相对磁导率；Bm和λm分别为饱和漏磁感应强度和饱和磁致伸缩系数。其中，μ，Bm，λm只跟材料性质相关，在固定材料下，这三个系数为常数。

将式(7)进行变换，得到

(8)

将μσ代入式(6)中，有

(9)

在试件所处环境恒定，材料固定的情况下，Hp(y)的数值大小仅与应力大小有关，变化规律曲线为反比例函数。Hp(y)随着应力的增大单调递增。

根据式(9)可知，在弹性阶段，应力作用下的法向磁信号值Hp(y)会因为应力的增大而增大。屈曲部位产生应力集中，应力会相对于平均值显著增大，因此屈曲位置的磁特征量Hcon会呈现出规律变化。

3.2.2 下降阶段理论分析

屈服前的下降阶段，屈服部位的材料内部由于应力作用产生大量位错，这些位错会形成钉扎效应从而阻碍磁畴的运动，形成位错塞积，塞积部位将产生应力集中，屈曲部位率先达到材料屈服。

基于塑性应变的有效磁场强度的表达式为[22]

Hσp=-k|ε-εy|

(10)

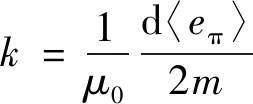
3.3 综合分析

综合上升下降阶段的理论分析可知，屈曲位置的磁特征量Hcon随荷载先升后降的变化规律可通过应力作用下磁场的变化以及应力产生的位错来解释。该变化规律也反映了应力在该检测点材料内部的变化情况。

Hcon先上升后下降的变化规律可以作为确定屈曲位置的判别依据，并且当Hcon的数值发生明显下降时，该变化是对屈曲进行的预警，此时需要注意防止该部位发生局部屈曲。

4 结 论

(1)金属磁记忆检测技术适用于受弯钢箱梁的屈曲监测。磁记忆特征参数Hcon可有效识别易发生屈曲的位置并能对屈曲进行预判，因此可作为监控参数，对施工中的钢构件进行失稳监测。

(2)易屈曲位置的磁记忆特征参数Hcon随着荷载变化具有一致性，表现为弹性阶段增长，试件屈服前发生明显下降。利用这一变化特征可以判别易发生屈曲的部位。

(3)当试件临近屈服时，磁记忆特征参数Hcon将发生明显下降，利用该特征可以对屈曲进行预警，预防灾害的产生。