薄壁圆管圆角模外翻过程的理论研究
张婉琪,尹冠生,姚如洋
(1.长安大学 理学院,西安 710064;2.湖南大学 机械与运载工程学院,长沙 410082)
薄壁金属圆管作为吸能元件被广泛应用于轨道车辆、汽车、飞行器和巷道支护等领域[1-4]。承受轴向荷载时,根据圆管尺寸和边界条件可将其塑性失效模式分为渐进屈曲、整体屈曲、翻转、膨胀、撕裂和收缩等[5-7]。与传统的渐进屈曲模式相比,翻转模式具有平稳的稳态翻转力且不存在过大的初始峰值载荷[8]。翻转模式根据变形区是否受力分为自由翻转与模具翻转,模具翻转又可根据模具形态分为圆角模翻转和锥形模翻转;根据翻转方向可将翻转模式分为内翻与外翻[9-13]。
圆管圆角模具外翻是一种模具制造安装简单且管件不需要预制成形的翻转模式,其翻转过程可分为临界状态之前的扩口卷曲阶段和之后的稳定阶段,实现稳定翻转时的翻转力称为稳态翻转力,是衡量翻转模式吸能特性的重要指标。由于扩口卷曲阶段的变形复杂且试验得到此阶段翻转力均低于稳态翻转力[14],所以大多数针对圆角模外翻模式的理论研究仅考虑稳定阶段的受力平衡或能量守恒以得到稳态翻转力。黄早文等[15-16]假设实现稳定翻转时圆管变形区为曲率半径不变的半圆,通过平衡法得到了考虑摩擦效应的稳态翻转力表达式并讨论了影响稳态翻转力的因素。El-Domiaty[17]通过理论分析得到翻转过程中子午线方向弯曲应变和周向拉伸应变约为其他应变分量的20倍,所以在用能量法求解稳态翻转力时其他应变可忽略不计。Niknejad等[18]同样假设变形区为曲率半径不变的半圆,不同的是假设管端卷曲360°并根据能量法建立理论模型,得到不考虑摩擦效应的稳态翻转力表达式。由于在稳态翻转力的计算中考虑了管端的收缩应变,所以该理论模型预测的稳态翻转力偏大。Leu[19]提出了一种圆管曲率在脱离模具瞬间改变的几何模型,即变形区为两个曲率不同的1/4圆。由于求解困难,最终仍然按照变形区为曲率半径不变的半圆求解。Yu等[20]采用了Leu所提出的几何模型,并假设管端翻转270°,根据能量法得到稳态翻转力理论解与曲率改变后的成形半径表达式。通过将其与试验结果[21]进行对比,发现其预测的成形半径较低。稳态翻转力与成形半径相关,因此导致其预测的稳态翻转力也存在一定误差。另外试验过程中圆管与模具之间的摩擦耗能不可忽略,而Niknejad等和Yu等将未考虑摩擦效应的理论结果与试验结果对比,其对比结果也是不可靠的。
理论分析的可靠性依赖于能准确体现翻转模式变形特点的几何模型。现有理论分析中的几何模型过于简化,不能准确体现试验得到的翻转模式变形特点。根据现有试验结果[22]和数值模拟得到的圆管圆角模外翻模式的变形特点,本研究提出一种新的描述圆管圆角模外翻模式的几何模型,基于该几何模型和能量法得到成形半径、临界位移和稳态翻转力理论公式并考虑摩擦效应的影响。通过数值模拟和试验结果验证理论分析的合理性,研究结果可为双壁管翻转成形及翻转模式吸能特性的研究提供参考。
1 圆管圆角模外翻模式的理论模型
1.1 几何模型与基本假设
圆角模外翻过程的几何模型轴向剖面,如图1所示。图1中:A,B,C,D四点为空间上位置不变的点,E,F两点为圆管上的点,其空间位置随着翻转过程的进行而改变(各点取所在位置中面上的点)。图1(a)为初始状态,此时圆管的长度为L,壁厚为t,中面半径为R,模具圆角半径为r,此时管端F处于空间位置A点,即A,F两点重合。当处于初始状态的圆管上端受到竖直载荷P的作用,圆管下端F沿圆角模具经过扩口卷曲等一系列过渡变形直至达到图1(b)所示的临界状态,此时圆管上的E,F两点分别与空间上的C,D两点重合。此后管端(EF)不再发生变形,圆管在C点发生反弯曲,从而形成与初始管壁平行且不断延伸的CE段,圆管翻转进入稳定阶段(见图1(c))。稳定阶段内ABC段为变形区,A点为变形起点,B点为圆管离开模具的点,C点为变形终止点。定义AB段曲率半径为扩口半径rA
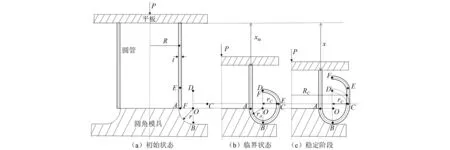
图1 圆管圆角模外翻过程几何模型轴向剖面图Fig.1 Axial profile of geometrical model of an external inversion tube over a circular die
rA=r-0.5t
(1)
则AB段曲率均为κA=1/rA。定义C点的曲率半径为成形半径rC,则C点曲率为κC=1/rC。假设AB段是曲率为κA的1/4圆弧,BC段是曲率由κA逐渐变为κC的曲线,CD(EF)段是曲率由κC逐渐降为零的曲线,曲率在BC和CD段均呈线性分布。
为简化分析过程,对翻转过程采取如下基本假设:
(1) 因为整个翻转过程发生塑性大变形,所以分析过程忽略弹性变形,即管的材料为各向同性的理想刚塑性材料,不存在包辛格效应。流动应力取屈服应力与极限应力的平均值
(2)
式中:σ0为流动应力;σs为屈服应力;σu为极限应力;
(2) 不考虑翻转过程中圆管壁厚和长度变化,且接触区(AB圆弧段)圆管与模具完全贴合;
(3) 忽略圆管内壁与模具之间的摩擦力,即外力做功完全用于管的塑性变形,考虑子午线方向弯曲和周向拉伸两种塑性变形,其余变形所耗能量可忽略不计,即
dW=P·v0=dWl+dWθ
(3)
式中:dW为外力在单位时间内做的功;P为翻转力;v0为A点变形速率;dWl为单位时间内子午线方向弯曲耗能;dWθ为单位时间内周向拉伸耗能;
(4) 仅考虑圆管在模具上轴向受压时能稳定翻转的工况,不考虑由圆管尺寸、初始缺陷和模具尺寸等原因造成的渐进屈曲和管端开裂两种失效模式。
1.2 成形半径
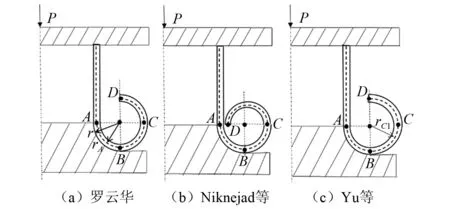
成形半径是描述翻转模式变形特点的重要物理量,也是后续准确预测稳态翻转力的基础。图2展示了3种不同几何模型的临界状态轴向剖面,其中A,B,C,D四点含义与图1中相同且AB段均为紧密贴合模具的圆弧段。对于圆管圆角模外翻,图2(a)是最简单且被采用最多的几何模型。该几何模型假设AD段是保持曲率不变的3/4圆弧,即管端按扩口半径翻卷了270°。图2(b)所示的几何模型假设AD段是保持曲率不变的圆,即管端按扩口半径翻卷了360°,未考虑由于A,D两点在空间上不能重合所造成的AD段的曲率变化。上述两种几何模型均假设管端翻转过程的曲率不变,仅管端翻转角度不同。因此这两种几何模型的成形半径均等于扩口半径,这与Gupta的试验结果有所不同。基于此Yu等研究了图2(c)所示几何模型,BD段仍为圆弧段,但曲率半径不再与AB段相同,在B点曲率半径由rA突变为rC1,即为该几何模型的成形半径
(4)
与已有试验结果和数值结果相比,式(4)得到的成形半径仍然有较大误差且在后续稳态翻转力的计算中忽略了B点的曲率突变。基于此本文提出了图1所示变形区曲率连续变化的几何模型,修正式(4)给出的成形半径表达式得到成形半径rC的经验公式
(5)
对于已知尺寸的圆管,求解关于模具半径r的方程rA=rC得到使得成形半径等于扩口半径的临界模具半径rm
(6)
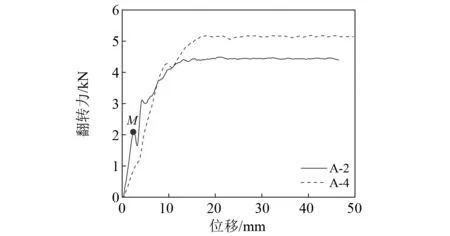
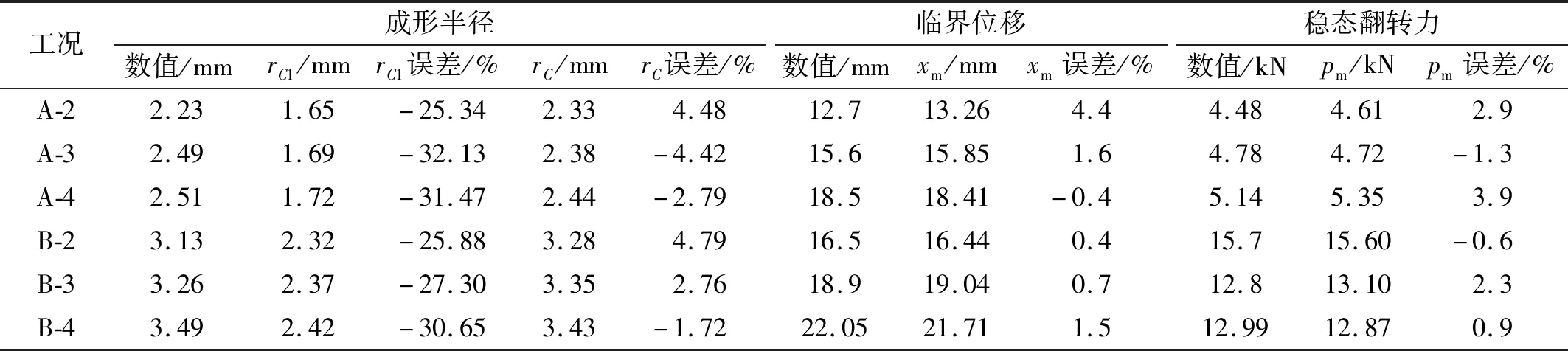
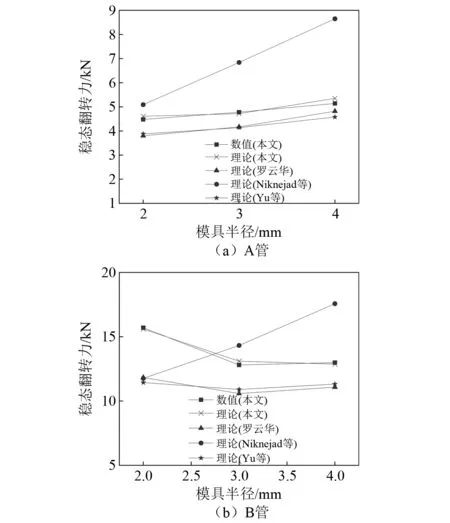
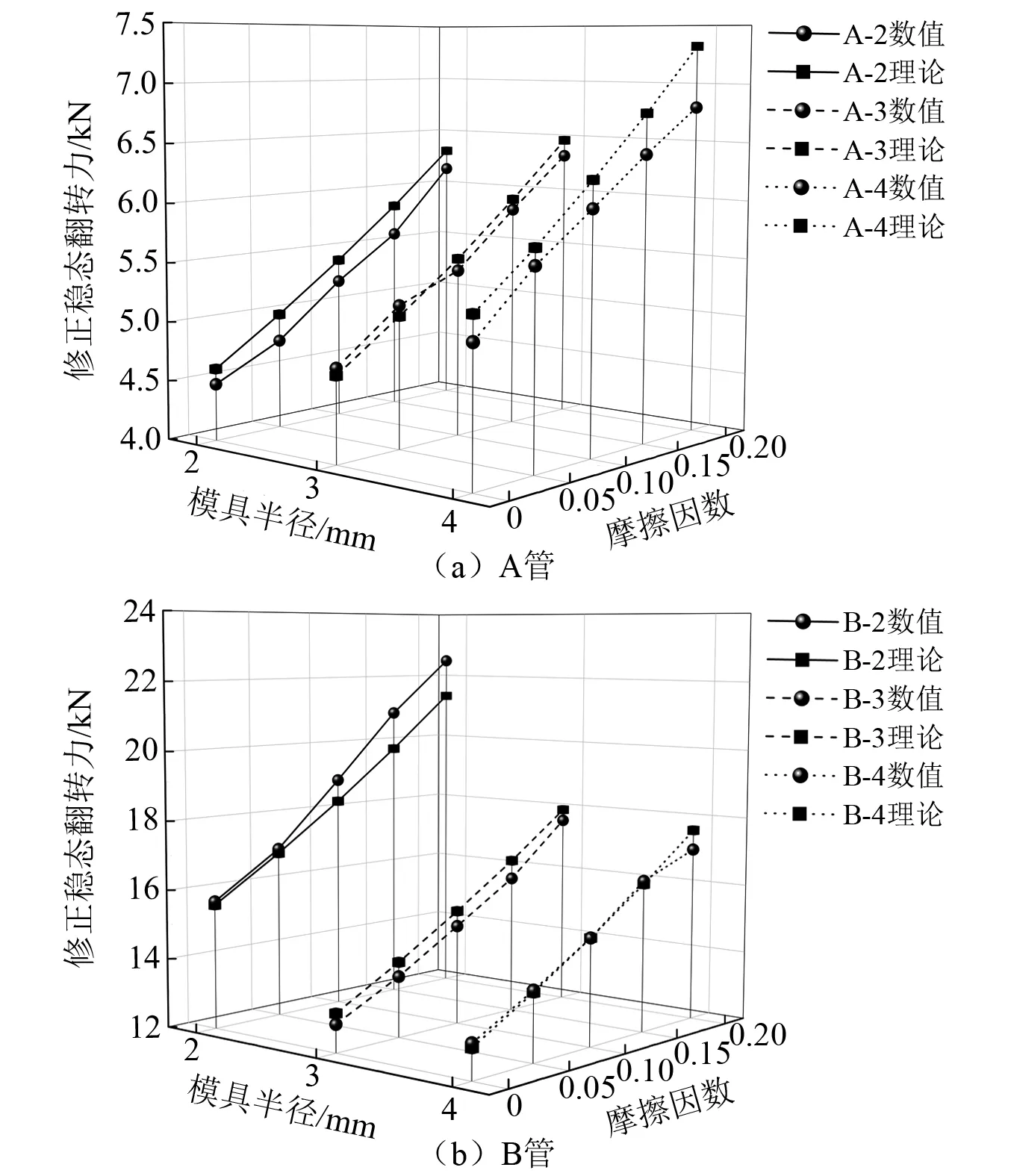
即当r 本文将圆管翻转到临界状态时,其上端下移的位移定义为临界位移xm,即上端位移到达临界位移以后,翻转进入稳定阶段。由于在1.1节中假设圆管长度不变,所以临界位移等于圆管下端F依次经过A,B,C,D四点的位移,由图1几何模型得AB段弧长为 (7) 由于曲率在BC段呈线性分布,取BC段的平均曲率κBC为 (8) (9) 同样,得到CD段平均曲率和弧长为 (10) (11) 因此,临界位移xm为 xm=SAB+SBC+SCD= (12) 临界位移是本文提出的描述翻转过程的物理量,目前还未有关于临界位移的讨论,但可根据其定义得到图2中各几何模型对应的临界位移 (13) xmb=2πrA=2π(r-0.5t) (14) (15) 式中,xma,xmb和xmc分别为计算图2(a)~图2(c)中ABCD段曲线长度得到的临界位移。 图2 不同几何模型临界状态轴向剖面Fig.2 Axial profile of geometrical model of different geometric models 如图1(c)所示,稳定阶段子午线方向曲率在变形区起止点(A,C两点)发生突变,在整个变形区是连续变化的。变形区起点(A点)曲率由零突变为κA,则A点曲率突变所引起的子午线方向弯曲耗能为 (16) (17) 因此,BC段子午线方向弯曲耗能为 (18) 式中,Ss,vs分别为坐标s位置的横截面面积与变形速率,根据体积守恒有Ssvs=S0v0。则 (19) C点曲率由κC突变为零,则C点曲率突变所引起的子午线方向弯曲耗能为 (20) 式中,SC,vC分别为C点的横截面面积与变形速率,根据体积守恒有SCvC=S0v0。 由式(16)~式(20)得到在单位时间内圆管子午线方向弯曲耗能为 (21) 在变形区ABC的翻转过程中,圆管中面半径由R增加至RC,由图1得几何条件:RC=R+r+rC-0.5t,所以周向周长增加所引起的拉伸应变为 (22) 则在单位时间内圆管周向拉伸耗能为 (23) 将式(21)和式(23)代入式(3)得到不考虑摩擦效应的稳态翻转力Pm为 (24) 即为 (25) 为了简化计算,在上述理论模型中没有考虑圆管与模具之间的摩擦效应。但是在翻转过程中,圆管与模具之间的摩擦耗能也会对翻转模式产生较大的影响,甚至当摩擦力较大时会影响圆管能否成功翻转。基于能量法预测翻转力的理论模型均未考虑摩擦耗能。在圆管翻转过程中,假设摩擦耗能独立于塑性耗能,参照由平衡法得到的稳态翻转力中的摩擦因数项,得到考虑摩擦效应的修正稳态翻转力为 (26) 式中,f为圆管与模具之间的摩擦因数。 为了验证理论分析的合理性,使用有限元软件ABAQUS /Explicit对圆管圆角模外翻过程进行数值模拟。由于圆管在整个翻转过程中的几何形状和边界条件均关于圆管中心线轴对称,所以在数值模拟时采用如图3所示的轴对称模型。上部平板和下部圆角模具均假定为刚体,选用2节点线性轴对称离散刚体单元RAX2对其进行网格划分。圆管选用铝管,表1给出其材料参数。将标准拉伸试验得到的工程应力-应变曲线(如图4所示)转化为真实应力应变数据并应用到数值模拟的计算中。采用4节点双线性轴对称单元CAX4R对圆管进行网格划分,沿着圆管厚度方向划分4~5个单元。采用A、B管两种尺寸的圆管,两种管的长度与中面半径相同(L=80 mm,R=20 mm),A管壁厚为0.5 mm,B管壁厚为1.0 mm。加载时约束上部刚性平板除轴向位移以外的所有自由度和下部圆角模具的所有自由度。对上部刚性平板按照平滑幅值曲线施加位移60 mm,加载时间为0.06 s,从而保证翻转过程为准静态[24]。分别设置圆管内表面、下端面与圆角模具为面面接触,圆管上表面与平板下表面为面面接触,圆管自身各表面为自接触,摩擦因数设为0。表2给出6种设计工况。 图3 圆管圆角模翻转的有限元模型Fig.3 Numerical mode of an external inversion tube over a circular die 表1 铝管的材料参数Tab.1 Material properties of the aluminum tubes 图4 材料工程应力-应变曲线Fig.4 The tensile stress-strain diagram of the tube material 表2 设计工况Tab.2 Design conditions 数值模拟可以得到各工况翻转过程的变形模式和力-位移曲线,结果显示6种工况都实现了圆管的成功翻转。图5给出工况A-2、工况A-3和工况A-4扩口卷曲阶段、临界状态和稳定阶段的变形模式及其对应的圆管上端位移。各工况扩口卷曲阶段给出两个典型时刻的变形模式:第一个时刻圆管与模具空隙最大,第二个时刻圆管与模具完全贴合。稳定阶段给出任一时刻的变形模式。有限元建模中给定上板位移60 mm,加载时当位移增大到一定值,圆管外壁与上板接触形成双壁管受压,力会随之瞬间增大,定义此时位移为翻转最大位移。位移到达最大位移以后的变形不在本文讨论范围内,因此只截取最大位移之前的数据得到工况A-2和工况A-4的力-位移曲线(如图6所示)。根据变形模式与力-位移曲线可以得到各工况的成形半径、临界位移与稳态翻转力的数值结果。 图5 翻转各阶段的变形模式Fig.5 Deformation modes at each stage of the inversion process 图6 翻转模式的力-位移曲线Fig.6 Force-displacement curves of inversion modes 图5给出各工况扩口卷曲阶段两个典型时刻的变形模式。由此显示在扩口卷曲阶段的初始,圆管下端与模具之间存在空隙,随着圆管上端不断下移,圆管下端逐渐贴合模具,并随着模具圆角半径r逐渐增大,此现象逐渐减弱。上述现象说明在扩口卷曲阶段数值模拟给出的变形模式与理论分析中假设的圆管与模具始终紧密贴合不符合,但该现象仅在模具圆角半径较小时会引起一个远小于稳态翻转力的局部初始峰值载荷(图6中的M点)。因此在分析翻转模式吸能特性时,可以不考虑其对所保护部件或乘客的伤害。 由临界状态变形模式的几何特征可以得到成形半径和临界位移,进而可以得到稳态翻转力、总能量吸收等衡量圆管圆角模外翻模式吸能特性的指标,因此临界状态变形模式的准确预测有重要意义。由图5给出的各工况临界状态变形模式可以看出变形区的曲率是不断变化的,且工况A-2的成形半径明显大于其扩口半径,而工况A-4的成形半径明显小于其扩口半径。对比数值结果与图2给出的3种几何模型以及图1(b),可看出本文的几何模型更接近数值模拟得到的变形模式。为了进一步验证本文提出的几何模型的正确性,需定量的证明由几何模型得到的成形半径与临界位移理论表达式的可靠性。 表3给出各工况成形半径、临界位移和稳态翻转力的数值结果、理论结果及两者相对误差,其中成形半径rC、临界位移xm和稳态翻转力Pm理论结果分别由式(5)、式(12)和式(25)得到,Yu等的成形半径理论值rC1由式(4)得到。由表3可知与数值结果相比,成形半径rC1较低且相对误差较大,在-30%左右;成形半径rC的相对误差远小于rC1的相对误差,最大相对误差为4.79%。这说明本文所提出的成形半径rC与数值结果更加吻合。根据式(6)得到A管的临界模具半径为2.61 mm,B管的为3.92 mm,由表3可得模具半径小于圆管对应临界半径的工况(A-2、B-2和B-3),其成形半径数值结果大于扩口半径;模具半径大于圆管对应临界半径的工况(A-3、A-4和B-4),其成形半径数值结果小于扩口半径,这与理论模型符合。为进一步验证本文成形半径表达式的合理性,将成形半径理论结果与现有试验结果进行对比。图7给出中面半径为24.35 mm、管壁厚度为1.3 mm的圆管在不同圆角半径模具上翻转的成形半径理论值和试验结果,结果显示本文成形半径的理论值rC依然比理论值rC1更接近试验结果。 表3 成形半径的理论值与数值结果Tab.3 Theoretical results and numerical results of forming radius 图7 成形半径的理论结果与试验结果对比Fig.7 Comparison of theoretical results and experimental results of forming radius 由表3得到本文提出的临界位移理论结果与数值结果吻合较好,最大的相对误差为4.4%。为了进一步验证本文临界位移理论结果的准确性,对比临界位移理论结果xma,xmb,xmc,xm和数值结果。图8给出A、B两种圆管在不同模具半径下的各临界位移结果,对比结果表示本文提出的临界位移xm与数值结果更加吻合。理论结果与数值结果均显示对于同一尺寸的圆管,当圆角半径增大时,临界位移也随之增大。临界位移的可靠性验证除了能进一步确认几何模型的正确性,还是从理论上准确预测圆管翻转模式总能量吸收的基础。总能量吸收是衡量部件吸能特性的一个重要指标[25]。对于圆管圆角模翻转模式,总能量吸收可分为到达临界状态之前扩口卷曲阶段和整个稳定阶段的吸能两部分计算。扩口卷曲阶段的吸能根据临界位移以前的力-位移曲线积分得到,稳定阶段的吸能由稳态翻转力与稳态位移(最大位移减去临界位移)的乘积得到。因此临界位移的准确预测对于翻转模式吸能特性的研究有重要意义。 图8 临界位移的理论结果与数值结果对比Fig.8 Comparison of theoretical results and numerical results of critical displacements 关于变形模式、成形半径以及临界位移的讨论验证了本文几何模型的可靠性,这初步说明基于此得到的稳态翻转力表达式的合理性。表3表明稳态翻转力理论结果与数值结果吻合较好,最大相对误差为3.9%。为了进一步验证本文关于稳态翻转力理论模型的正确性,将其与Yu等、Rezvani等和Yao等的理论结果进行对比。为消除流动应力的不同选择带来的影响,将Yu等、Rezvani等和Yao等表达式中的流动应力替换为本文采用的流动应力。由于本文以及Rezvani等和Yao等在理论模型建立时都未考虑摩擦效应,将Yu等表达式中的摩擦因数取为0。图9对比各工况下稳态翻转力的4种理论结果和数值结果,对比结果表明:Rezvani等在多数工况下过大的预测了稳态翻转力;Yu等和Yao等的理论结果较为接近,均略低于数值结果;本文理论模型更加符合数值结果。 图9 稳态翻转力的理论结果与数值结果对比Fig.9 Comparison of theoretical results and numerical results of steady inversion force 上述数值结果均基于摩擦因数选取0的数值模型得到,验证了不考虑摩擦效应时理论模型的合理性。在实际翻转过程中,圆管与模具之间存在不可忽视的摩擦效应,因此需要进一步考虑摩擦效应以对比理论结果与试验结果。当圆管与模具之间的摩擦力过大时,会导致圆管不能成功翻转,本节仅讨论在适当范围内的摩擦效应对描述翻转模式各物理量的影响。将2.1节数值模型中的摩擦因数从0改为0.05,0.10,0.15和0.20,其余设置不变进行数值计算。数值结果显示摩擦因数的改变对于临界位移与成形半径影响不大,所以3.2节中关于成形半径与试验结果的对比依然可靠。 根据式(26)得到各工况在不同摩擦因数下的修正稳态翻转力Pmf,图10给出各工况下修正稳态翻转力理论结果与数值结果随摩擦因数的变化。数值结果与理论结果均显示稳态翻转力会随着摩擦因数的增大而增大且两者吻合较好,这说明根据式(26)考虑摩擦因数对稳态翻转力的影响是可靠的。通过将本文理论结果与Niknejad等、Gupta等和Rezvani等的试验结果对比,初步得到摩擦因数取值在0.15附近时,修正的稳态翻转力更符合试验结果。这与黄早文等研究中提到的在用矿物油做润滑剂时,摩擦因数取0.15~0.16符合。在运用本文理论分析预测实际工程或指导试验设计时,应根据具体的圆管材料、模具材料以及润滑条件选取适当的摩擦因数。 图10 稳态翻转力随摩擦因数的变化Fig.10 The change of steady inversion force with friction coefficient (1) 对比已有理论模型,本文提出的理论模型更符合数值结果和现有试验结果。成形半径、临界位移和稳态翻转力理论预测与数值结果的误差均低于5%。 (2) 临界位移为本文首次提出的描述圆管圆角模外翻模式的物理量,其不仅能验证几何模型的正确性,还是后续计算整个翻转过程总能量吸收的关键。根据已有理论的几何模型和本文关于临界位移的定义得到其对应的临界位移理论结果并与本文理论结果对比,结果显示,本文临界位移理论公式更接近数值结果。 (3) 圆管与模具之间的摩擦效应对成形半径和临界位移的影响较小,对稳态翻转力的影响不可忽略。在运用本文理论模型预测实际工程或指导试验设计时应采用修正稳态翻转力理论公式,摩擦因数通常取0.15或根据具体摩擦条件取值。1.3 临界位移
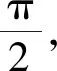
π(0.75r+1.25rC-0.375t)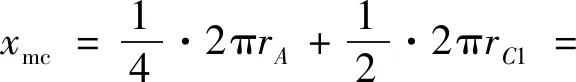
1.4 稳态翻转力

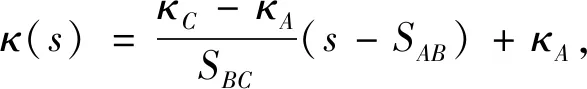
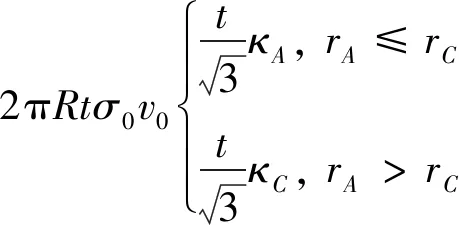
1.5 摩擦因数修正
2 数值模拟
2.1 有限元建模
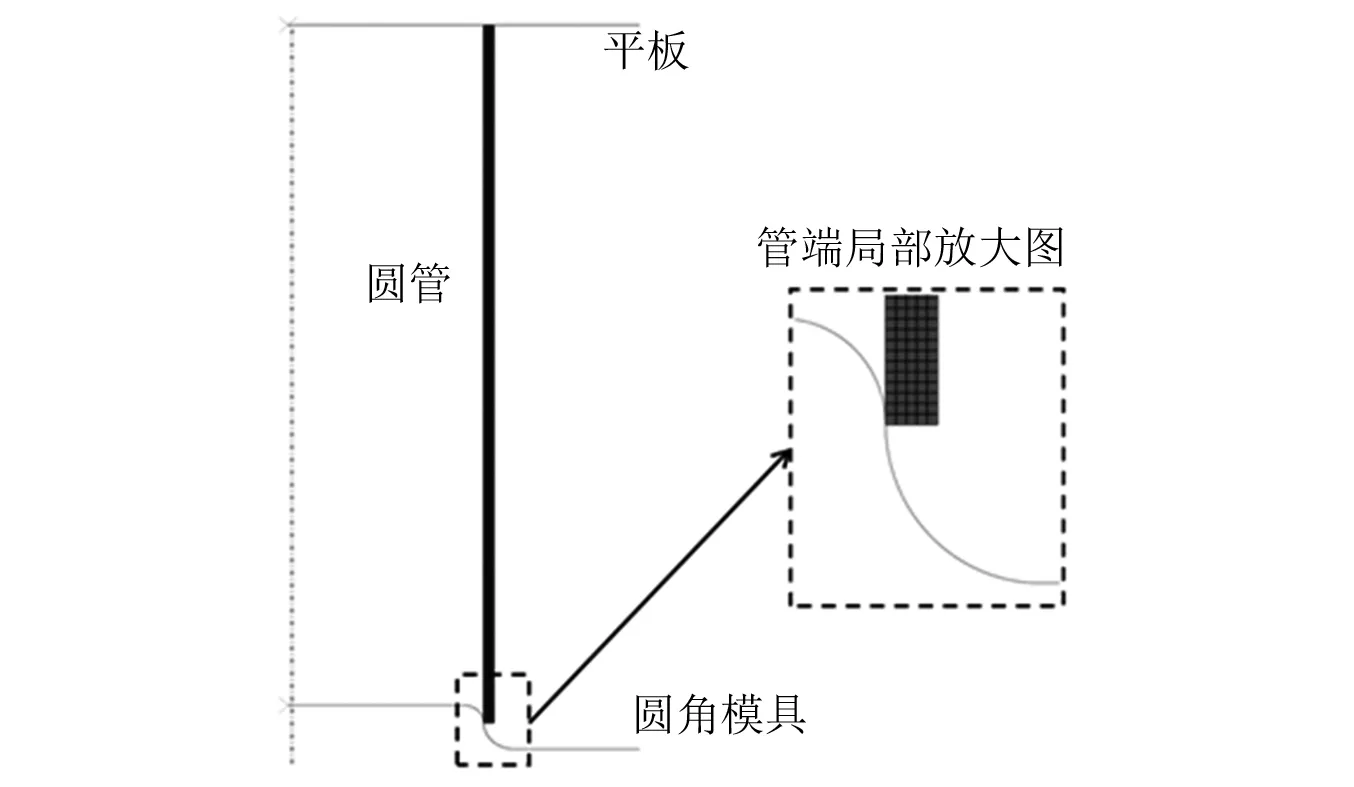

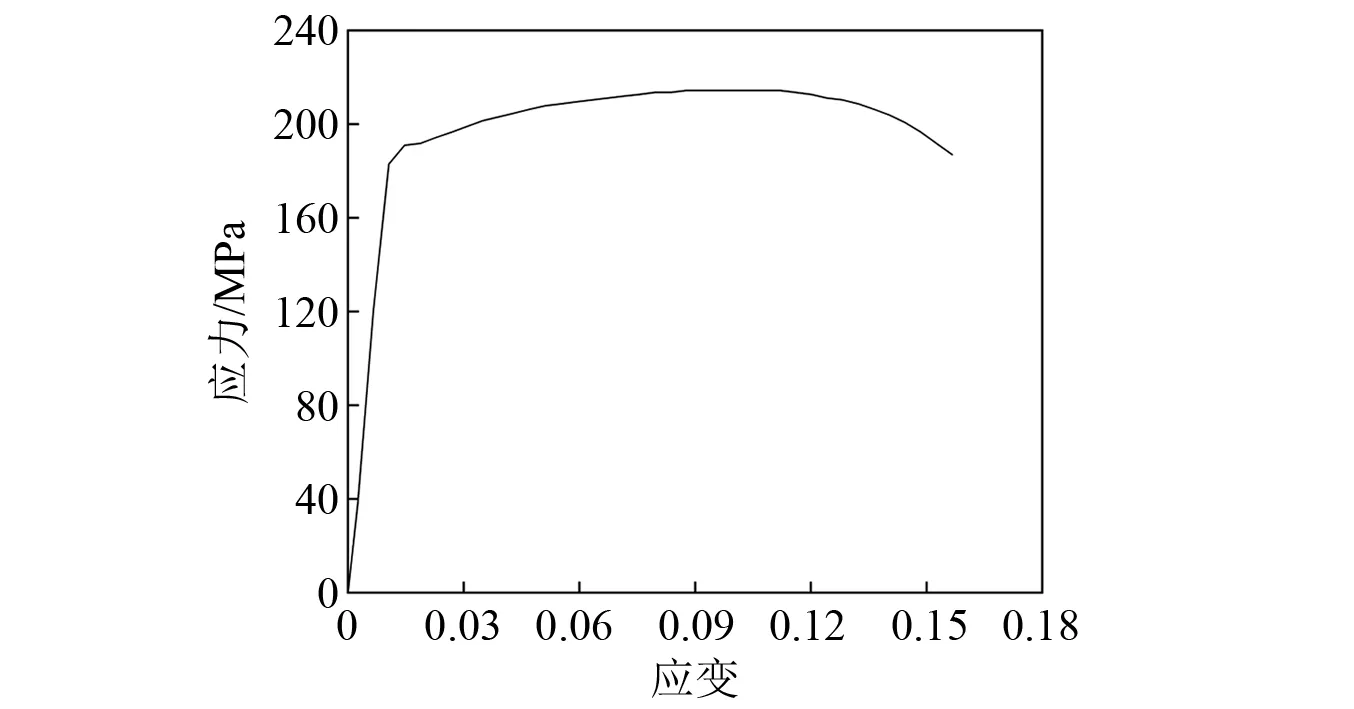

2.2 数值结果

3 结果与分析
3.1 变形模式
3.2 成形半径、临界位移和稳态翻转力

3.3 摩擦效应的影响
4 结 论

