周期和随机联合激励作用下滞回系统非平稳随机响应的一种近似方法

孔 凡，沈子恒，何 卫，李书进

(1.武汉理工大学 土木工程与建筑学院，武汉 430070;2.中国地质大学(武汉) 工程学院，武汉 430074)

随机振动分析方法已被广泛地应用于工程科学的各个领域。由Booton[1]和Caughey[2]先后提出的统计线性化(statistical linearization,SL)方法是解决非线性系统随机振动最常用方法之一[3]。该方法的可靠性在几个典型的非线性随机动力系统中得到了验证，例如Duffing振子[4-5]、Van der Pol振子[6]、双线性[7]和Bouc-Wen模型[8]滞回动力系统等。然而，多数研究均集中于随机动力系统的平稳随机动力响应。

在地震工程领域，随机过程常用来描述地震动的随机性。目前，常见的随机地震动的平稳色噪声模型有金井清模型[9]、Clough-Penzien模型[10]、欧进萍-牛荻涛模型[11]和彭凌云模型[12]等。然而，实际地震加速度的数据记录表明地震动中存在明显的非平稳特性。研究表明，该特性对结构响应的影响不可忽略。Priestley[13]提出通过调制函数描述非平稳激励，为随机过程非平稳性提供了理论基础。基于此理论，大量研究者[14-19]开始使用非平稳激励模拟地震动或大气湍流。

有些实际工程中，工程或机械系统会同时受到确定性周期和随机激励的联合作用，例如地震中的旋转机械[20-21]、风力作用下行进中的列车[22]、大气湍流作用下的风力发电机叶片[23]以及近场地震作用下的结构[24]等。Bouc-Wen模型常用来模拟隔震结构的滞回特性[25-26]。因此，求解非平稳随机激励和确定性周期激励共同作用下的Bouc-Wen滞回系统动力响应是有实际意义的。

最近，本文作者和其他作者发展了非线性(包括滞回)系统在联合激励作用下平稳响应的统计线性化方法[27-28]。本文可视为上述平稳方法在非平稳响应方面的拓展：它是一种用于求解非平稳随机激励和确定性谐波联合作用下，单自由度滞回系统非平稳响应的统计线性化方法。该方法的关键在于：将系统响应分解为确定性谐波和零均值随机分量之和。由此，将原运动方程等效地化为两组耦合的、分别以确定性和随机动力响应为未知量的非线性微分方程。随后，利用统计线性化方法处理非平稳随机激励下的随机运动(子)方程，并由此导出关于随机响应分量二阶矩的Laypunov微分方程。将Laypunov微分方程与确定性非线性运动微分方程联立，并利用龙格库塔法求解。最后，数值算例验证此方法的适用性和精度。

1 动力学方程

单自由度滞回系统在确定性谐波和非平稳随机激励联合作用下的运动方程为

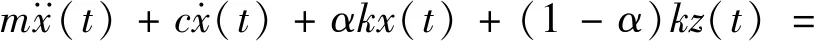
(1)

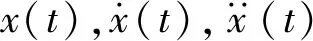
Q(t)=a(t)QS(t)

(2)

式中：QS(t)为谱强度为S0的零均值白噪声；a(t)为确定性调制函数；z(t)为系统滞回位移，采用Bouc-Wen滞回模型描述

(3)

式中，A,n,γ和β均为Bouc-Wen系统参数。注意到，本文发展的方法亦可用于非平稳色噪声和其他非线性滞回模型的情况；限于篇幅，不在本文中讨论。特别地，当n=1时，式(3)化为

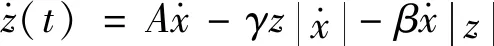
(4)

假定式(1)的非线性响应x(t)和z(t)均可分解为确定性谐和分量和零均值随机分量之和，即

(5)

(6)

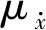
(7)

对式(7)两边求期望得

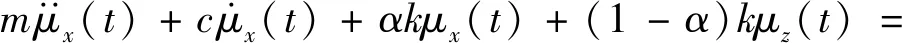
(8)

用式(7)减去式(8)得

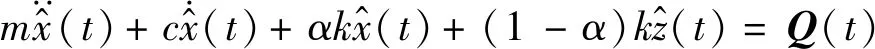
(9)

同样地，将式(5)和式(6)代入式(4)中，可得

(10)

对式(10)两边求期望得

(11)

用式(10)减去式(11)得

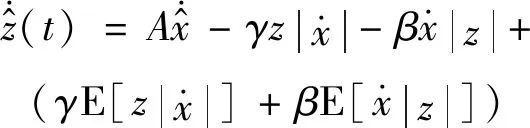
(12)

其中，利用统计线性化方法经常采用的响应高斯假定，可得

(13)

(14)

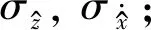
2 统计线性化方法求解随机分量

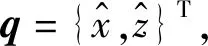
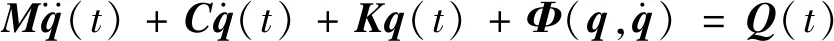
(15)

式中：

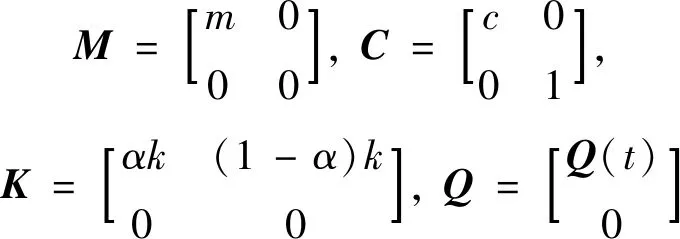
分别为质量、阻尼、刚度矩阵和激励向量；Φ=[φ1,φ2]T，且φ1=0

(16)

将式(15)线性化为

(17)

式中，

分别为等效阻尼和等效刚度矩阵，且

(18)

(19)

(20)

(21)

(22)

(23)

采用线性随机振动的状态空间方法，求解等效线性系统中未知响应统计量σx,σz和ρ与等效参数ke和ce的关系。为此，使用状态空间方法表示式(17)，如下

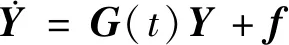
(24)

其中,

(25)

通过与式(24)对应的Lyapunov微分方程

(26)

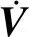
(27)

其中，

Λ(t)=2πS0a2(t)

(28)

考虑到V是对称阵，则可将式(26)化为关于6个独立未知量(v11,v12,v13,v22,v23,v33)的6个耦合的代数方程，即

(29)

(30)

(31)

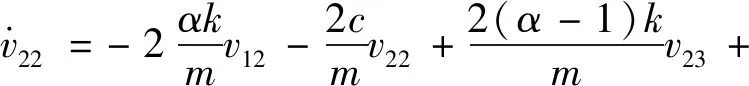
(32)

(33)

(34)

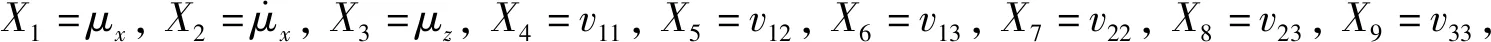
3 数值算例

3.1 简谐激励频率与幅值均不变的情况

取正归化Bouc-Wen滞回系统的参数为m=1,ζ=0.3,ωn=1；取共振情况的确定性谐波激励参数为F0=0.5,ω0=1。此时，运动方程为

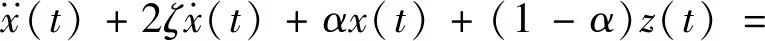
(35)

其中，

Q(t)=a(t)QS(t)

(36)

a(t)=exp(-μt)-exp(-υt)

(37)

式中：μ，υ为控制调制函数a(t)非平稳性的参数；QS(t)的谱强度取为S0=4ζ/π。

利用软化和硬化Bouc-Wen系统作为算例验证所提方法的适用性。其中，软化Bouc-Wen系统的滞回参数取为A=1,γ=0.5,β=0.5,n=1,α=0.1；硬化Bouc-Wen系统β=-0.35,γ=0.65，其他参数与软化系统相同。本文建议方法(proposed method,PM)与Monte Carlo模拟(Monte Carlo simulation,MCS)的结果对比如图1～图4所示。MCS中涉及的样本激励由谱表现法生成。图1和图2为软化Bouc-Wen系统响应的对比结果：可见，本文建议方法得到的响应均值和标准差与15 000个样本的MCS估计的结果吻合良好，且能较好地捕捉到响应的非平稳性。注意到，本文建议方法与MCS得到的响应(特别对于滞回位移)标准差均出现了类似简谐的抖动，这是由于确定性和随机性响应耦合效应造成的。

为方便对比，对MCS和建议方法得到的标准差函数求时间平均，即

(38)

式中：T为时长；σ(t)为求得的标准差，并依此进行误差分析。在图1(a)所示的确定性位移响应对比中，二者得到的稳态幅值相差-3.75%；图1(b)中，二者得到的标准差时间平均值相差-2.67%。图2(a)和图2(b)所示的滞回位移响应对比中，二者得到的均值稳态幅值相差-5.12%，而标准差时间平均值相差-2.98%。

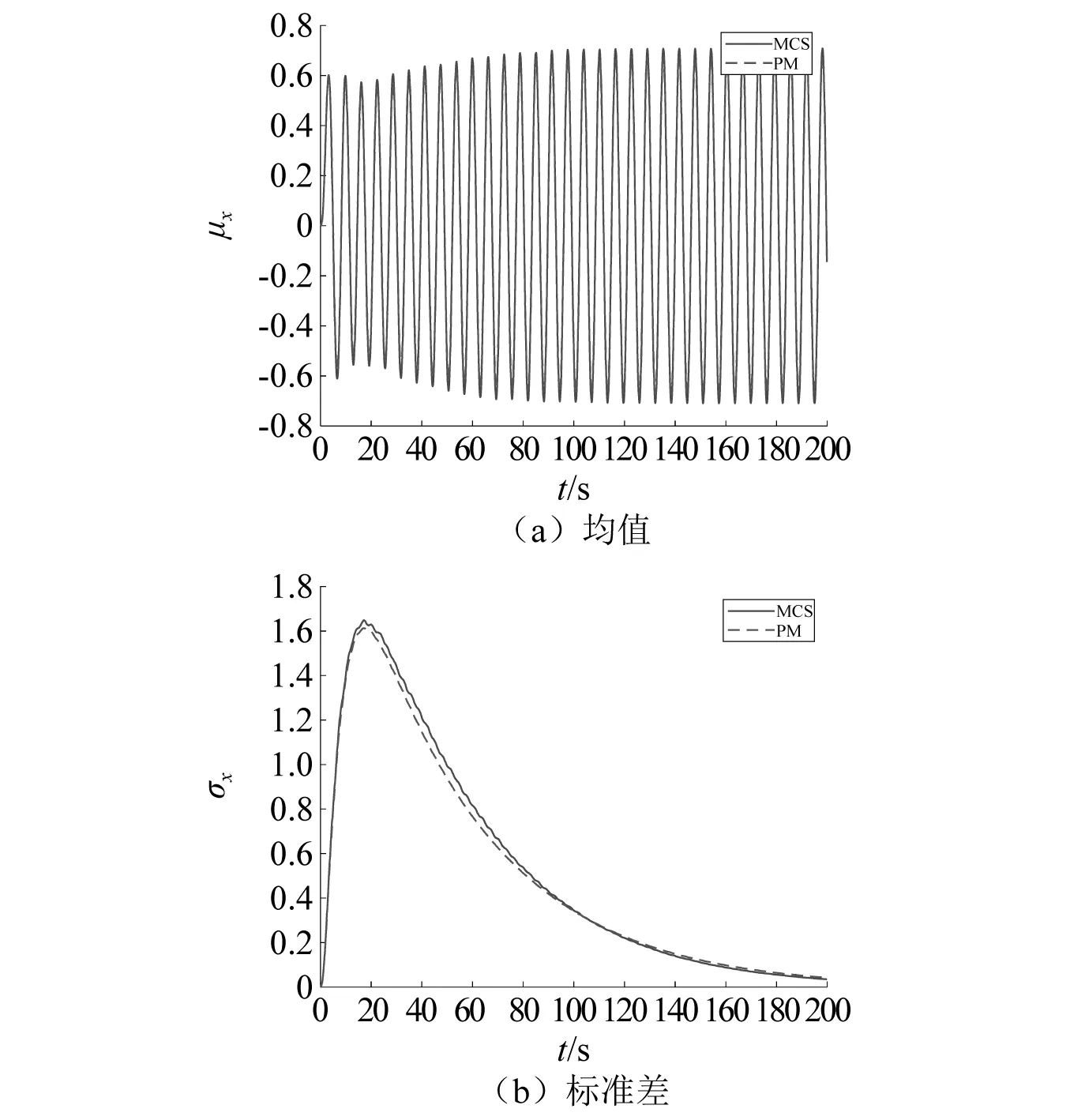
图1 联合激励下软化Bouc-Wen系统在联合激励下的位移Fig.1 Displacement of a softening Bouc-Wen system subjected to combined excitation

图2 联合激励下软化Bouc-Wen系统在联合激励下的滞回位移Fig.2 Hysteretic displacement of a softening Bouc-Wen system subjected to combined excitation

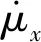
(39)

同样地，所建议方法对硬化系统也有很好的计算精度，如图3和图4所示。具体而言，二者得到的位移响应均值的幅值相差-7.08%，标准差时间平均值相差-6.12%；滞回位移均值的幅值相差-9.93%，标准差时间平均值相差-4.32%。以上误差均在统计线性化方法的合理范围之内。

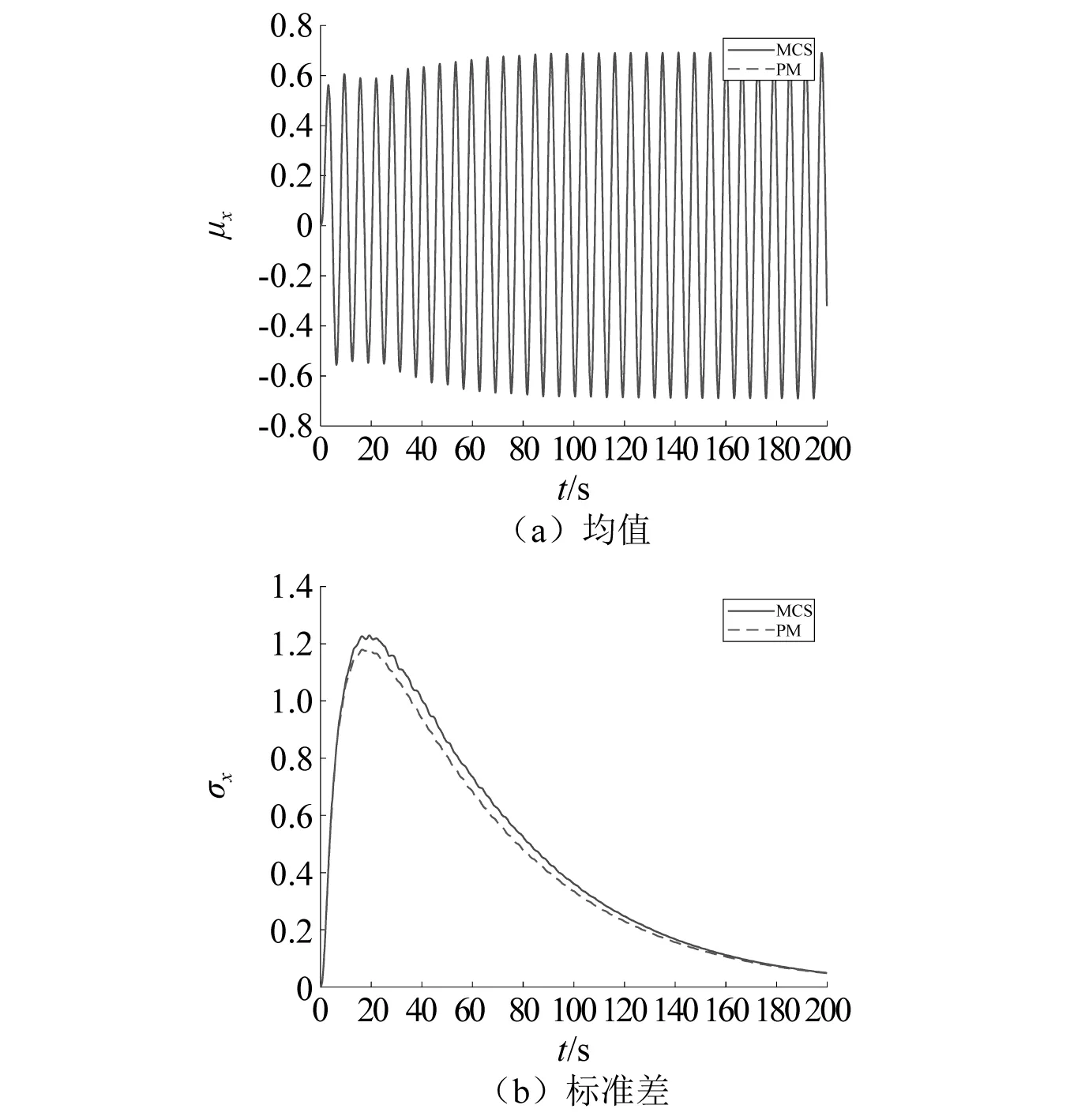
图3 联合激励下硬化Bouc-Wen系统在联合激励下的位移Fig.3 Displacement of a hardening Bouc-Wen system subjected to combined excitation

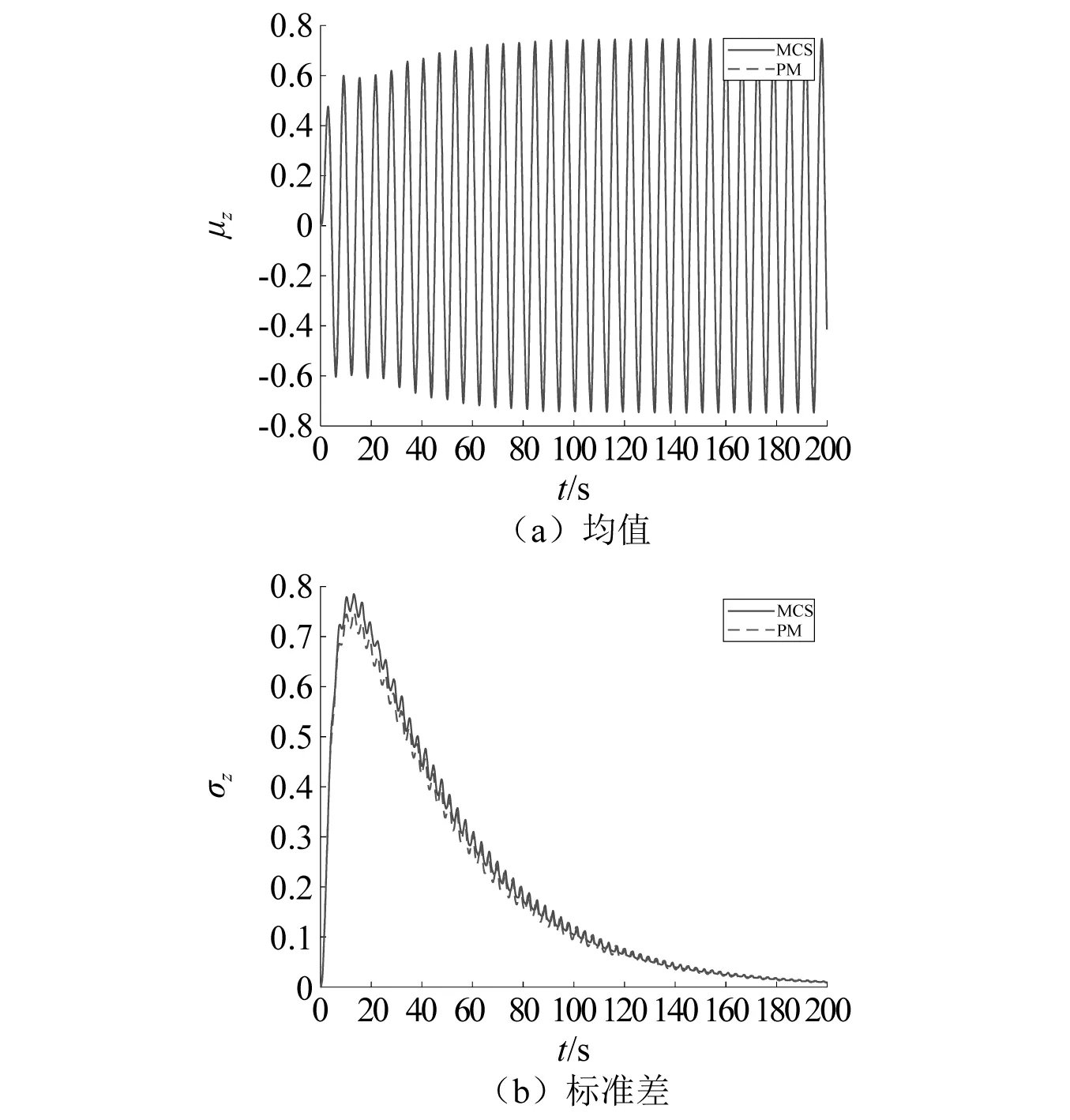
图4 联合激励下硬化Bouc-Wen系统在联合激励下的滞回位移Fig.4 Hysteretic displacement of a hardening Bouc-Wen system subjected to combined excitation

本文的参数选择均使滞回曲线饱满，呈明显非线性。软化Bouc-Wen系统和硬化Bouc-Wen系统在谐波与随机激励样本联合激励样本联合作用下的滞回曲线由图5(a)和图5(b)所示。可见，随机扰动使系统响应不能形成闭合的滞回环。

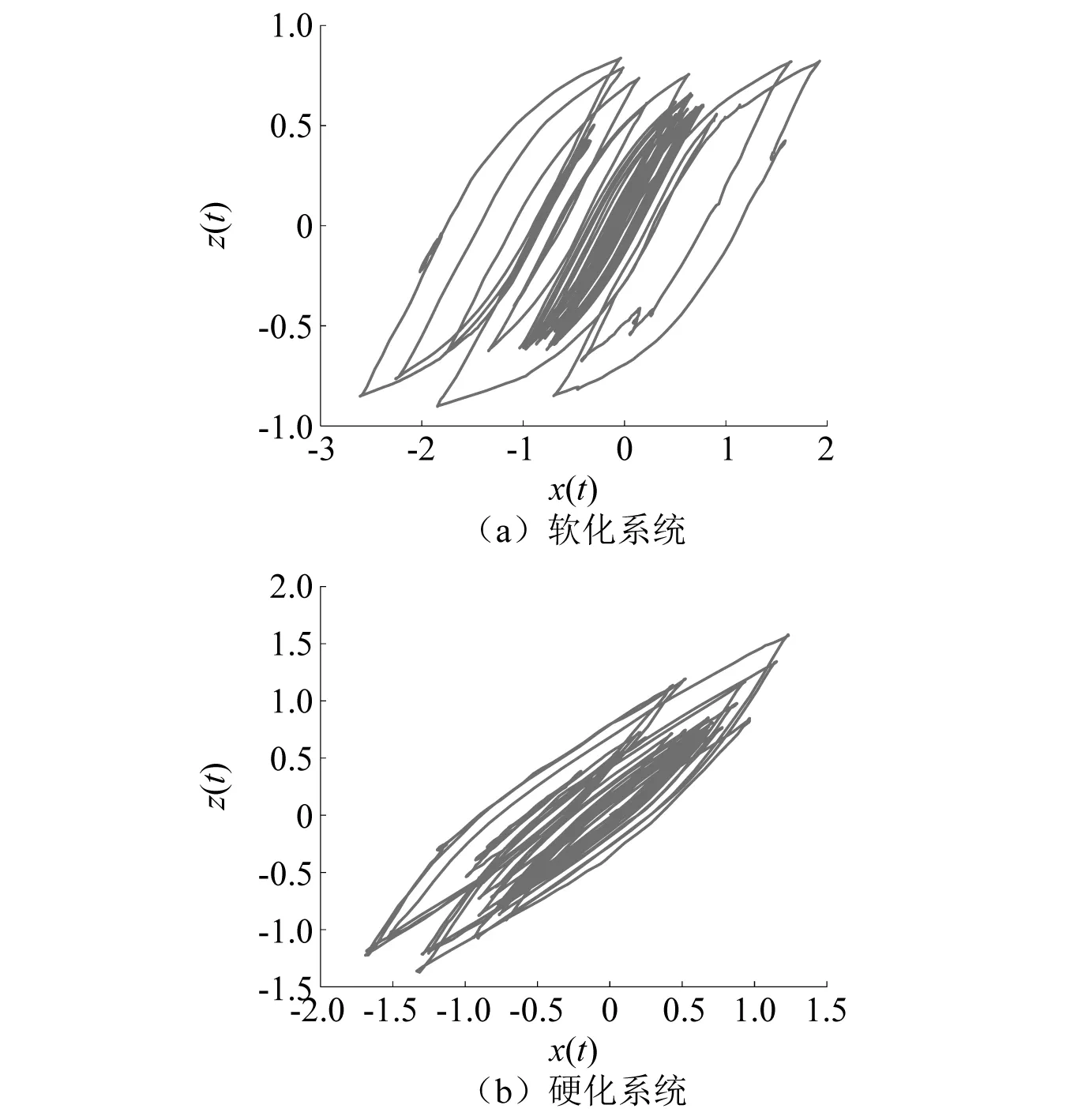
图5 联合激励下Bouc-Wen系统在联合激励下的滞回环样本Fig.5 A sample hysteresis loop of two Bouc-Wen models subjected to combined excitation

3.2 简谐激励频率的影响

当谐波激励接近系统自振频率或者谐波激励幅值增大时，谐波响应分量μx,μz增大。由于确定性谐和分量作用下的运动方程与零均值随机分量作用下的运动方程是耦合的，所以，谐波响应分量会对随机响应分量产生影响。因此，讨论谐波激励在不同幅值与频率下该方法的适用性是非常重要的。

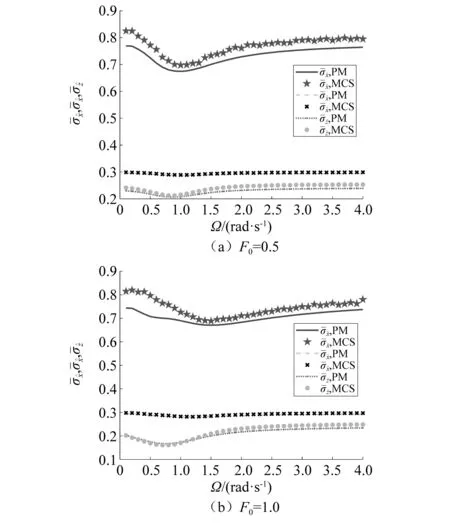
图6 联合激励下软化Bouc-Wen系统随机响应分量标准差的时间平均与谐和激励频率之间的关系Fig.6 Time-averaged standard deviation of the stochastic response component of a softening Bouc-Wen system subjected to combined stochastic excitation and harmonic excitation with different frequencies

当谐波激励的幅值分别为F0=0.5和F0=1.0时，本文所提出方法与Monte Carlo模拟得到的确定性响应稳态幅值对比如图7(a)和图7(b)所示。由图可见，该情况下本文所建议方法得到的结果与Monte Carlo模拟得到估计值符合良好。此外，本文所建议方法的精度在确定性响应稳态幅值方面要高于标准差时间平均值。

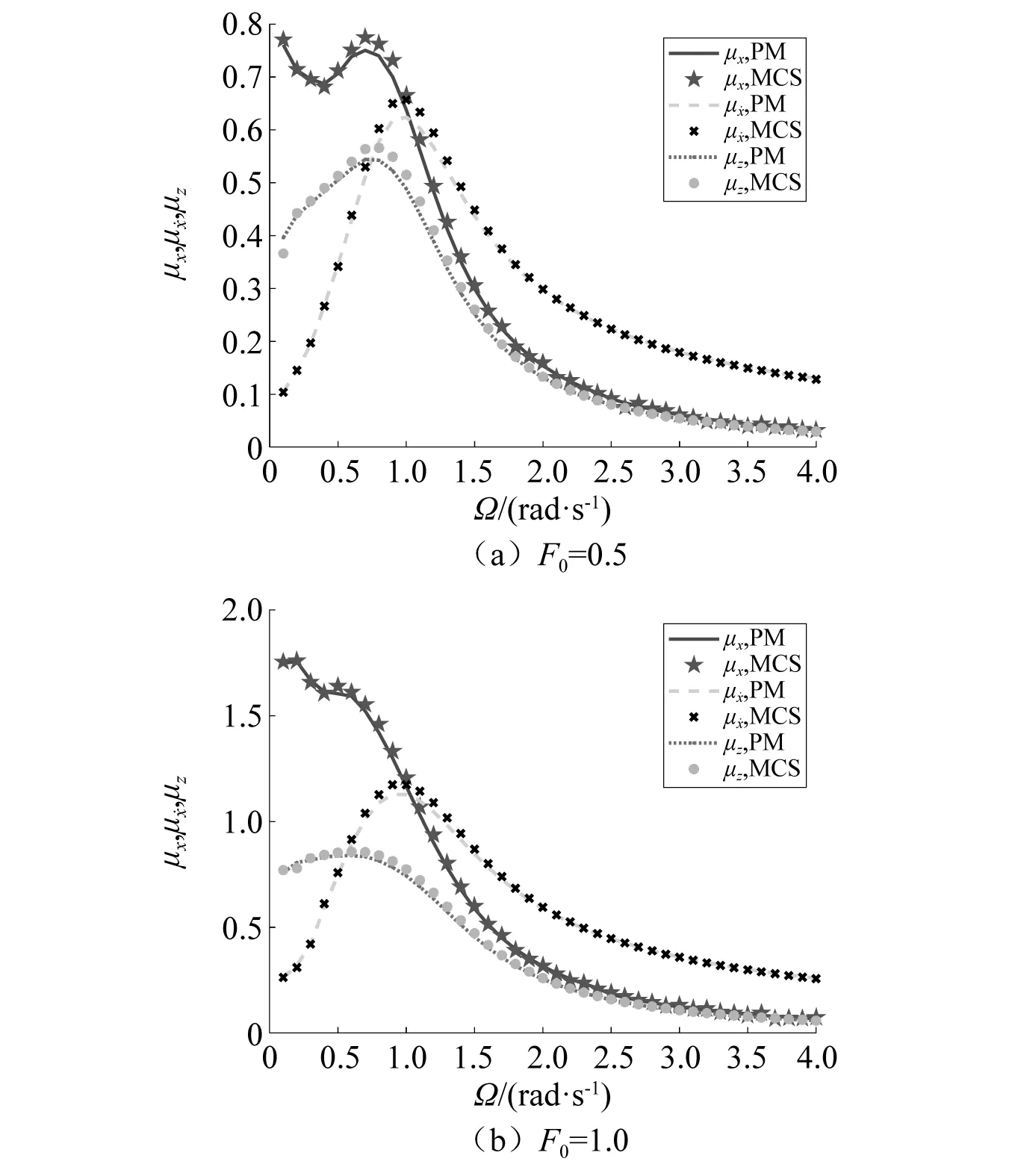
图7 联合激励下软化Bouc-Wen系统均值响应分量平稳幅值与谐和激励频率之间的关系Fig.7 Amplitude of the stationary deterministic response component of a softening Bouc-Wen system subjected to combined stochastic excitation and harmonic excitation with different frequencies

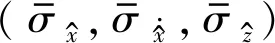
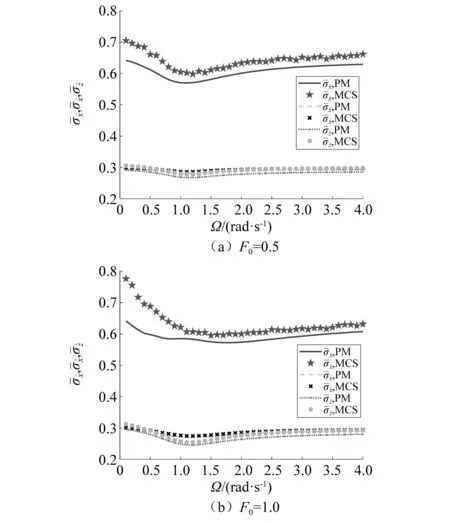
图8 联合激励下硬化Bouc-Wen系统随机响应分量标准差的时间平均与谐和激励频率之间的关系Fig.8 Time-averaged standard deviation of the stochastic response component of a hardening Bouc-Wen system subjected to combined stochastic excitation and harmonic excitation with different frequencies

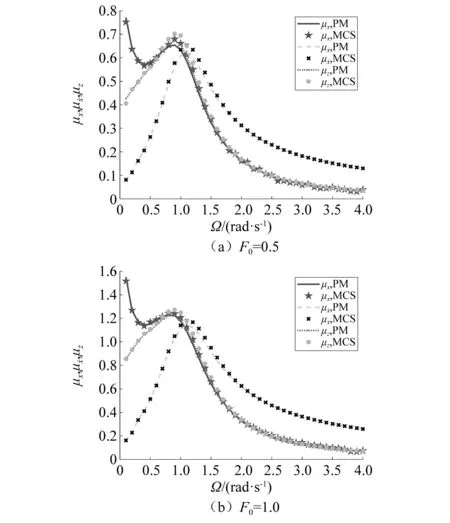
图9 联合激励下硬化Bouc-Wen系统均值响应分量平稳幅值与谐和激励频率之间的关系Fig.9 Amplitude of the stationary deterministic response component of a hardening Bouc-Wen system subjected to combined stochastic excitation and harmonic excitation with different frequencies

3.3 简谐激励幅值的影响

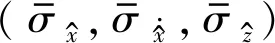
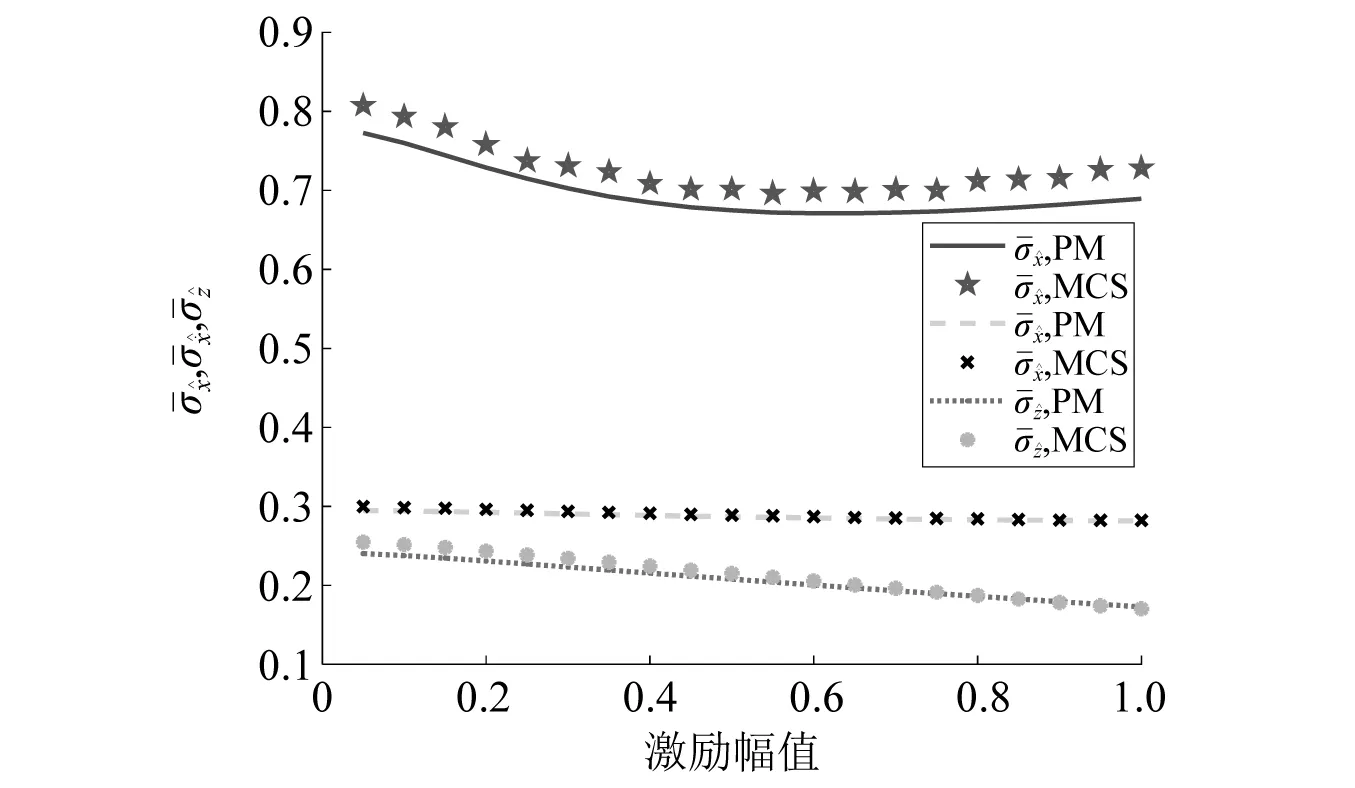
图10 联合激励下软化Bouc-Wen系统随机响应分量标准差的时间平均与谐和激励幅值之间的关系Fig.10 Time-averaged standard deviation of the stochastic response component of a softening Bouc-Wen system subjected to combined stochastic excitation and harmonic excitation with different amplitudes

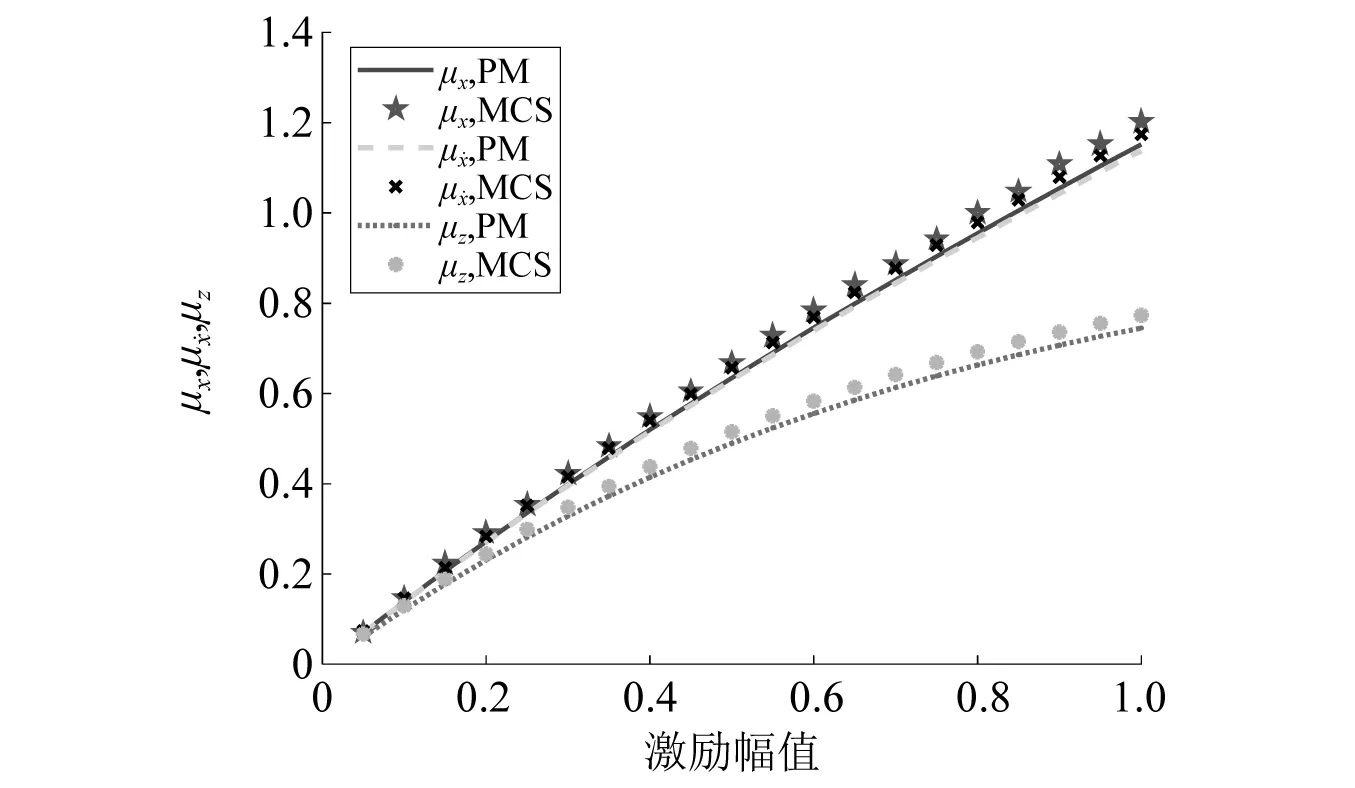
图11 联合激励下软化Bouc-Wen系统均值响应分量平稳幅值与谐和激励幅值之间的关系Fig.11 Amplitude of the stationary deterministic response component of a softening Bouc-Wen system subjected to combined stochastic and harmonic excitation with different amplitudes

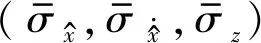
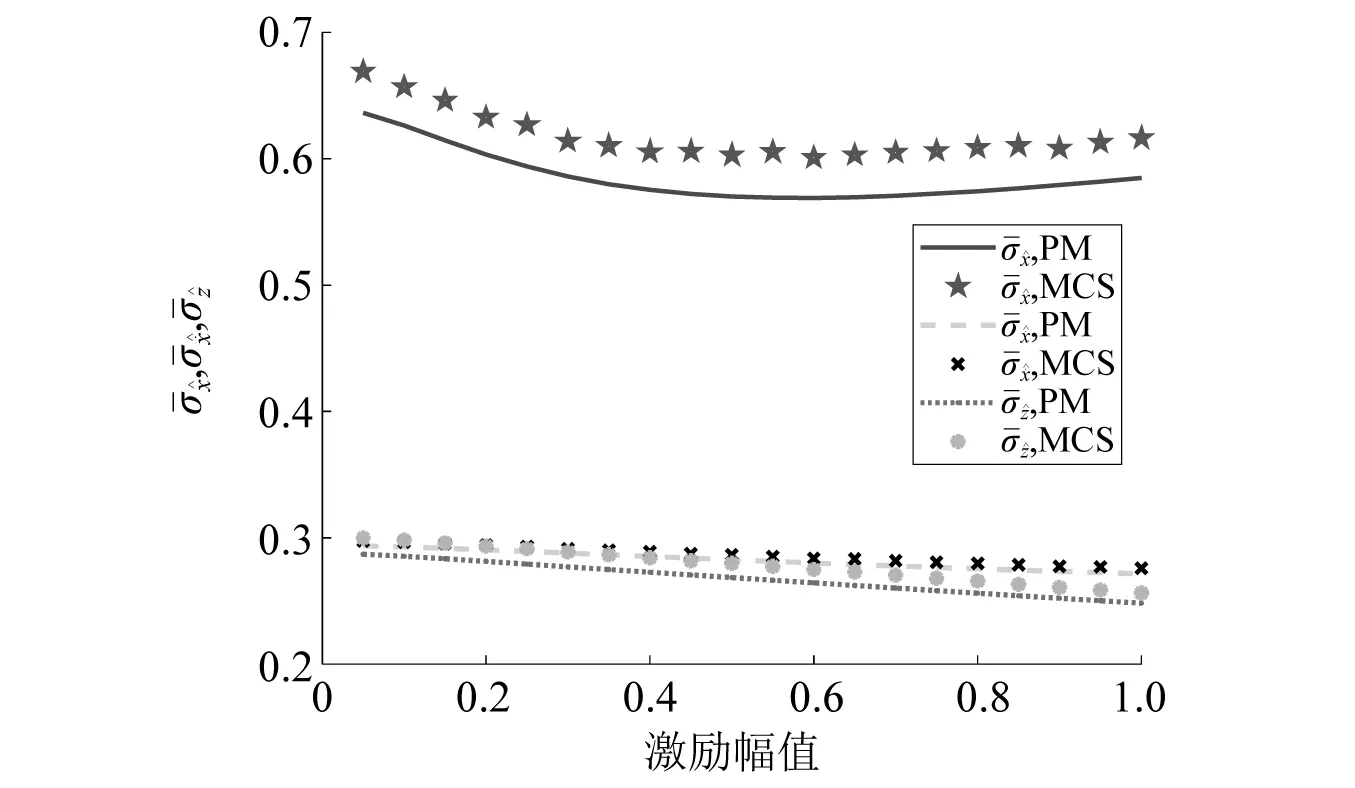
图12 联合激励下硬化Bouc-Wen系统随机响应分量标准差时间平均与谐和激励幅值之间的关系Fig.12 Time-averaged standard deviation of the stochastic response component of a hardening Bouc-Wen system subjected to combined stochastic excitation and harmonic excitation with different amplitudes

图13 联合激励下硬化Bouc-Wen系统均值响应分量幅值与谐和激励幅值之间的关系Fig.13 Amplitude of the stationary deterministic response component of a hardening Bouc-Wen system subjected to combined stochastic excitation and harmonic excitation with different amplitudes

3.4 随机激励强度的影响

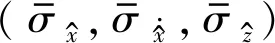
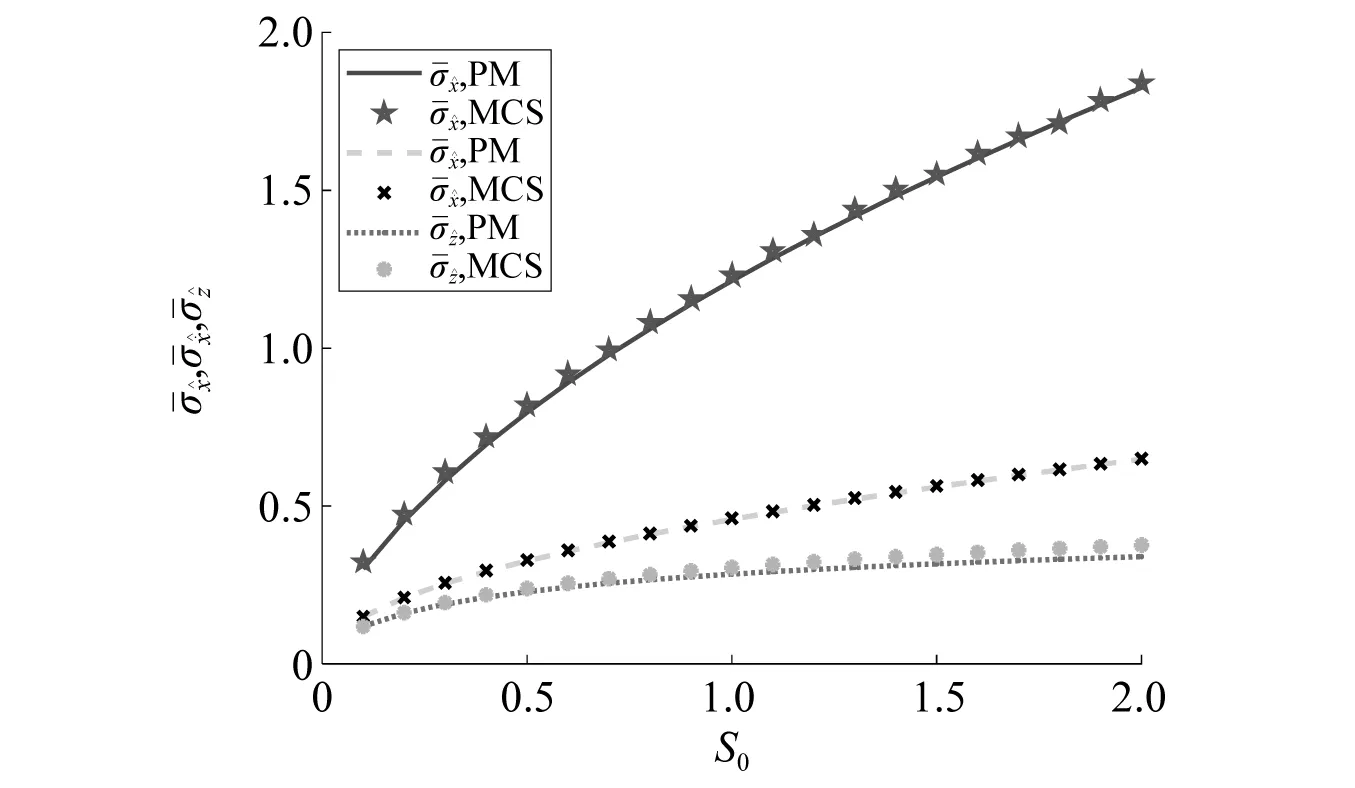
图14 联合激励下软化Bouc-Wen系统随机响应分量标准差与随机激励强度之间的关系Fig.14 Time-averaged standard deviation of the stochastic response component of a softening Bouc-Wen system subjected to combined harmonic excitation and stochastic excitation with different strength

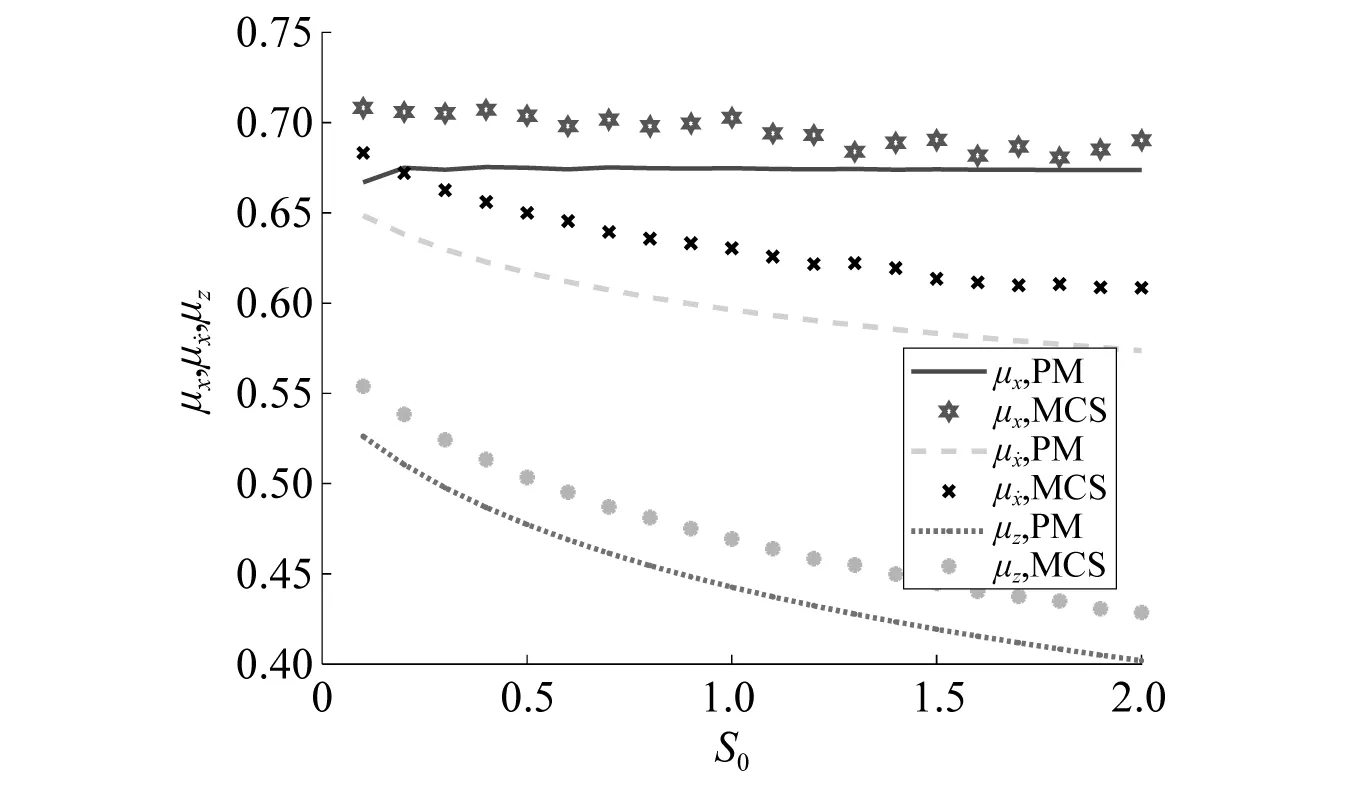
图15 联合激励下硬化Bouc-Wen系统均值响应分量平稳幅值与随机激励强度之间的关系Fig.15 Amplitude of the stationary deterministic response component of a softening Bouc-Wen system subjected to combined harmonic excitation and stochastic excitation with different strength

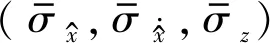
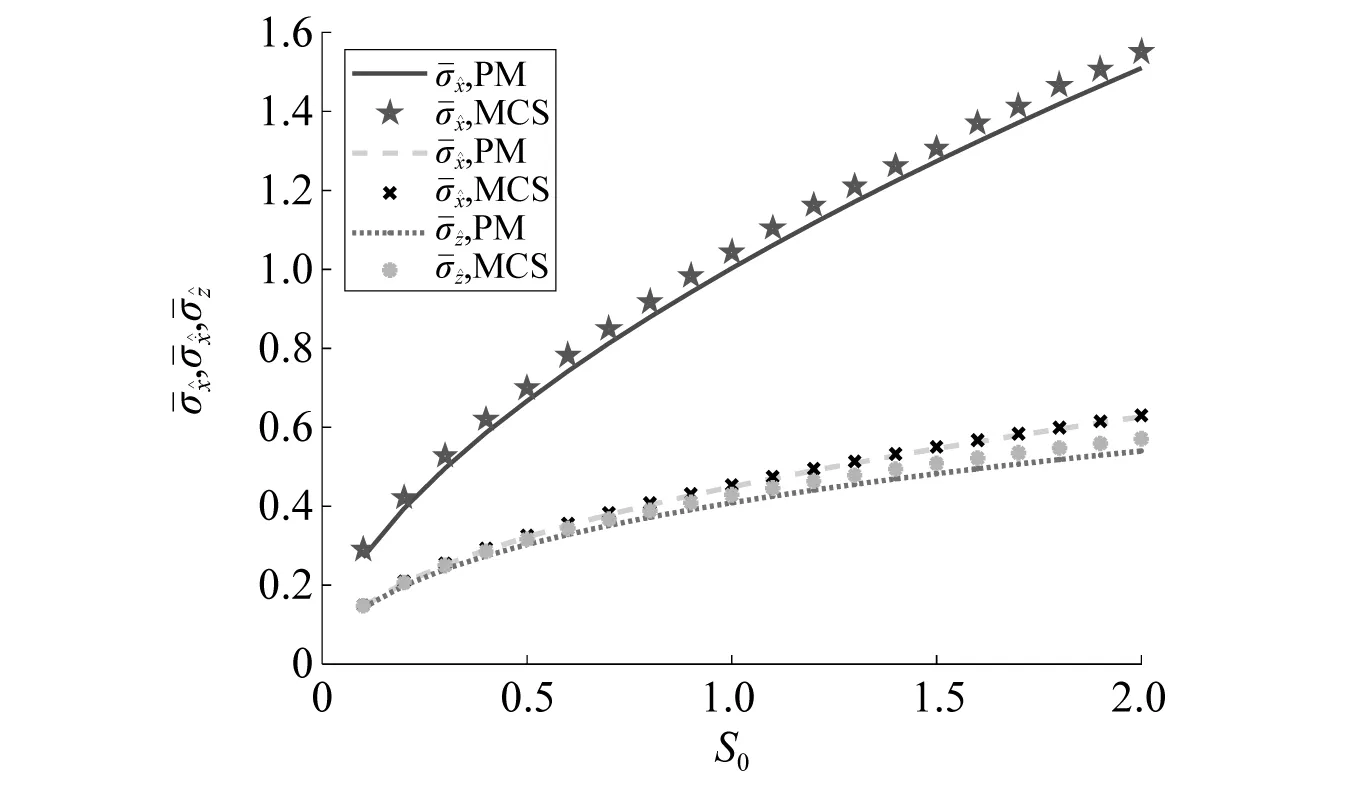
图16 联合激励下硬化Bouc-Wen系统随机响应分量标准差的时间平均与随机激励强度之间的关系Fig.16 Time-averaged standard deviation of the stochastic response component of a hardening Bouc-Wen system subjected to combined harmonic excitation and stochastic excitation with different strength

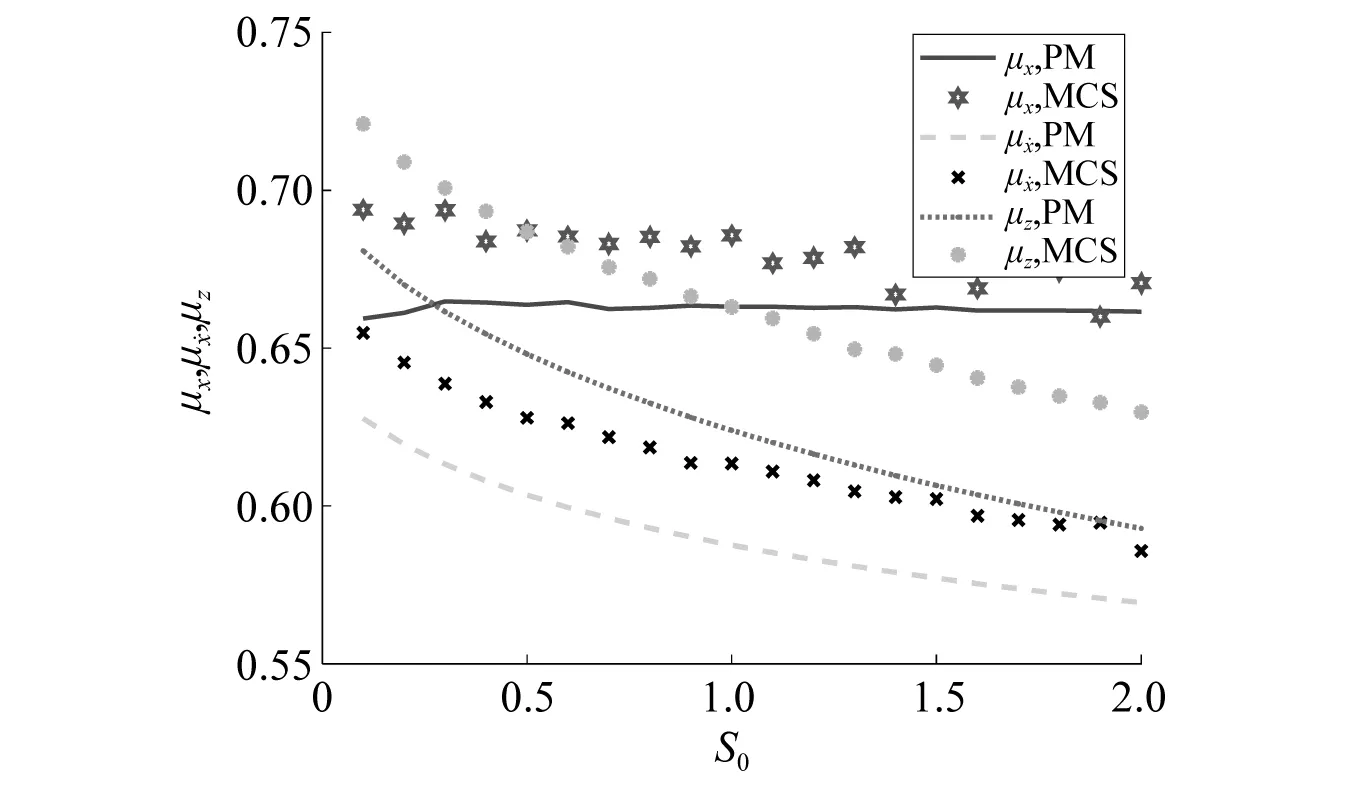
图17 联合激励下软化Bouc-Wen系统均值响应分量平稳幅值与随机激励强度之间的关系Fig.17 Amplitude of the stationary deterministic response component of a hardening Bouc-Wen system subjected to combined harmonic excitation and stochastic excitation with different strength

本文所建议方法对于不同的α的滞回动力系统同样适用，限于篇幅，兹不赘述。

4 结 论

本文提出了一种求解Bouc-Wen滞回系统在确定性谐波与非平稳随机激励联合作用下，非平稳响应的统计线性化方法。该方法将系统响应表示为确定性谐波和零均值随机分量之和，进而以两组耦合的非线性微分方程(分别以谐波和随机响应为未知量)等效地替代原滞回运动方程。随后，利用统计线性化方法处理非平稳随机激励下的随机运动方程，导出了关于随机响应分量二阶矩的Lyapunov微分方程。将Lyapunov方程与确定性非线性微分方程联立，并利用龙格库塔法求解了上述耦合微分方程组。最后，以软化和硬化Bouc-Wen系统为数值算例，在不同参数设置的情况下，对系统响应进行广泛的数值分析，验证了所建议方法的适用性。结果表明：在考虑的参数设置情况下，所建议方法具有合理的精度。

注意到，本文提出的基于统计线性化方法求解联合激励下滞回系统非平稳随机动力响应的思路，具有较大的适用性范围。因此，更适合于联合激励下工程结构系统随机动力分析。此时，利用Lyapunov方程求解等效多自由度线性系统的随机响应二阶矩时，其复杂程度随着自由度的增加而迅速提升。因此，可考虑使用状态空间内复模态分析的方法降低计算量。