横风作用下移动点湍流脉动特性风洞试验研究

李志国，张天翼，苏 益，王沛源，李明水

(1.西南交通大学 风工程试验研究中心，成都 610031；2.西南交通大学 风工程四川省重点实验室，成都 610031；3.重庆大学 山地城镇建设与新技术教育部重点实验室，重庆 400450；4.重庆大学 土木工程学院，重庆 400450)

在强侧风的作用下，火车、汽车和飞机等移动载具的行驶安全会受到重大影响。因此，研究行驶中车辆的侧向空气动力载荷及响应是十分必要的，这需要对车辆周边流场的湍流特性进行系统性研究和合理估计[1-3]。

湍流特性的常规研究是基于在固定点观测的风速脉动。但是，研究发现[4-7]，将固定点湍流特性应用于行驶中车辆的动态行为可能是不合理的。这种不合理性是由于缺乏对车辆与来流间相对运动的考虑，正如Connell[8-9]在研究快速旋转叶片遇到的湍流特性时首次描述的那样。作为输入项，行驶中的车辆所经历的风特性将直接关系到车辆空气动力学载荷及响应问题。为此，有必要将研究由传统的静止观测框架扩展至移动观测框架。

在描述流体速度场时通常采用两种视角：其一为依据欧拉表述法，在某一定点去捕捉一固定坐标系统中的每个空间点位在不同时间点的流动参数的变化；其二为拉格朗日表述法，即在保持静止的情况下对某一流体粒子进行跟踪观察。与上述两个观测法相对应，现有的研究在模拟和研究移动车辆历经的脉动风速时程时通常采用以下两种方法。其一与欧拉表述法相对应的，是静态流场模拟理论。Shinozuka[10]通过离散点提取和相邻点插值获得运动点当前位置的瞬时风速，建立了用于多变量随机过程仿真的谱表示方法。该方法已被许多研究人员开发和应用，他们通过增加模拟点的数量来补偿由人工散布引起的误差。然而，这种方法不可避免地导致作用在运动车辆上脉动风速的不连续性，可能引起附加的结构动力响应，这将与实际情况不符。此外，因脉动风场的空间相干性，插值方法亦不准确。显然，多元随机过程模拟方法效率低下，且无法真正揭示行驶车辆所历经的脉动风特性。对于另一种方法，Balzer[11]推导了高速车辆在任意方向湍流场中行驶时所遇到的湍流统计特性，并基于典型的等相关椭圆轮廓线提出了水平阵风的功率谱密度。他认为风速脉动的横向及纵向分量可忽略不计，而高速车辆的纵向分量占主导地位。随后，Cooper[12]采用与Balzer类似的方法，使用ESDU数据库[13]中强风(>10 m/s)的湍流统计模型，基于von Kármán的谱模型提出了移动车辆相关的功率谱密度函数，他开创性地考虑了横向脉动风速的影响。这种模拟移动单点随机过程的方法显着提高了模拟效率，并得到后来诸多研究人员的验证、应用及扩展，Cooper的理论模型也成为研究移动车辆风荷载及响应的理论基础。

然而，尽管理论研究发展了几十年，但很少有关于此问题的试验研究。其原因是由于常规边界层风洞的宽度有限，在风洞中很难实现以稳定的速度沿风洞宽度方向行驶一定的时间和距离，所以目前运动车辆历经的湍流脉动特性仍缺乏系统的试验研究。此外，应该指出的是，Balzer和Cooper的获得湍流特性的方法都涉及将车辆的速度叠加到现有的风特性上，以获得对行驶车辆所经历的湍流的预测。换句话说，他们使用基于基本假设的数值模拟将移动点实际经历的风时程与静止点处的观测值等同起来。实际上，参考系因运动而改变，即移动点历经的脉动风速时程及其统计特性是时间和空间位置的函数，这与假定中其仅为时间的函数的情况相反。

与上述两种表述法(欧拉法及拉格朗日法)相反，本文通过试验手段在移动点进行了风速时程的测量，以得到准确的、考虑了移动参考系的湍流特性。本文设计了一种可以使测量探针以中等速度在湍流场中移动的试验装置，并在大尺度边界层风洞中进行重复测量试验，以研究在移动点处观测的湍流脉动特性。因为垂直于移动方向的横风最为典型，所以本文仅研究了运动方向垂直于来流方向的工况，可以为其他风偏角下移动点湍流特性的研究提供参考。

基于可重复的长时间观测记录，本文通过风洞试验研究了不同风速-车速比下，移动点测得的湍流积分尺度、湍流强度、湍流脉动速度谱等湍流脉动特性。与传统方法相比，改变参考系以获得移动点所历经的实际湍流脉动特性将更加合理和准确。该方法为准确研究移动车辆的空气动力载荷及风致响应提供了基础，且对考虑横风对移动车辆的非定常气动力、行驶舒适性及安全性的影响具有重要的意义。

1 理背景

1.1 湍流积分尺度

湍流可以被认为是由均匀流传送的涡流的叠加，涡流的尺度和湍流能量在不同尺度上的分布决定了湍流的结构特征。湍流积分尺度是湍流脉动中含能涡的平均尺寸的度量，是确定阵风特性在空间中变化速度的重要尺度因子。因此，它们在结构荷载分析中的重要性不可忽略。实际上，积分尺度的大小决定了湍流对结构的影响范围。如果涡的尺度大于结构特征尺寸，则结构各部分上湍流脉动引起的动态载荷将被叠加。反之，动态载荷可能会相互抵消[14]。

(1)

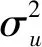
因湍流积分尺度是与湍流空间相关性相关的参数，因此最理想的分析方法是在空间中同时进行多点测量通过数值计算获得。不幸的是，目前多点同步测量尚很难实现。因此，根据Taylor冻结假设，通常将此过程简化为单点测量。如湍流涡旋随平均速度为U的流动迁移，则根据Taylor冻结假设，脉动速度u(x1,t+τ)可表示为u(x1-x,τ)，x=Ut，。根据假设，式(8)可改写为

(2)

此外，可直接由脉动速度的功率谱密度函数获得湍流积分尺度，以避免相关性的分析。庞加斌等[15]比较了几种常用的计算湍流积分尺度的方法，并验证了Taylor冻结假设的合理性，使用自相关函数直接积分法计算湍流积分尺度既简单又足够准确。

1.2 湍流脉动速度谱

如前所述，湍流总能量可认为是流动中每个涡旋能量贡献的总和。在各向同性湍流理论中，假设流场恒定且流动不可压缩，频谱张量可用总动能描述。1948年，von Kármán[16]结合了Kolmogorov和Loitsyansky的理论，提出了能谱的插值公式并得到两波数谱。需要注意的是，尽管谱理论是在波数域内表述的，但是大多数测量是在频域内进行。脉动风速功率谱密度的实质是描述湍流能量在各种频率下的分布密度，指出湍流中不同尺度的涡旋对湍流能量的贡献[17]。将湍流脉动风速谱在频域内表达，以u向为例可写为

(3)

关于移动车辆历经的湍流，早在1977年，Balzer根据Lumley和Panofsky对Davenport谱模型的修改式，率先提出了一种大气湍流影响理论。Balzer认为，对于地面高速行驶的车辆，脉动速度纵向分量的影响占据主导地位，而横向及垂直分量的贡献可忽略不计，且Taylor冻结假设在应用于行驶中的车辆时同样有效。而后，Balzer基于Taylor冻结假设，推导出移动车辆经过任意方向湍流场时历经的湍流统计特性。在此基础上，提出了纵向速度分量ρu′(τ)在湍流场中沿任意方向的自相关函数

(4)

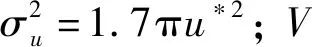
因此，与之相关的u分量湍流长度尺度可基于式(4)获得

(5)

Cooper采用与Balzer类似的方法，扩展了ESDU给出的大气湍流综合统计模型，以表述湍流速度相对于时间和空间的变化。与Balzer一样，Cooper同样认为Taylor冻结假设将适用于移动车辆，并提出了Taylor冻结假设的修改版本，概念图如图1所示。

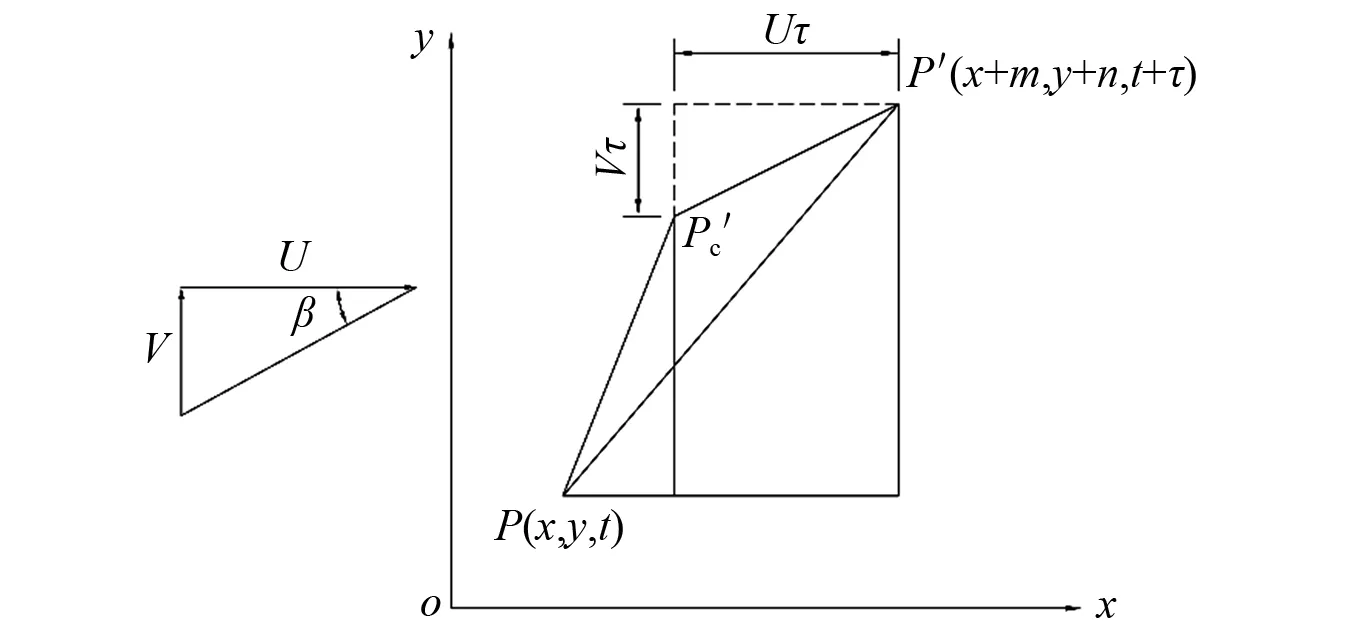
图1 冻结湍流场中原点位及等效点位概念图Fig.1 Geometry of physical and equivalent points in a frozen turbulent field

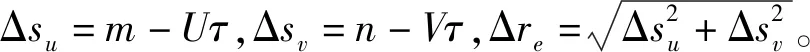
基于上述的冻结假设，当点位P′与P′e重合时，即m=0,n=0，则自相关函数ρu′(τ)为

(6)

(7)

式中，湍流积分尺度Lu采用ESDU中定义的合成长度尺度

(8)

cu=(U/UR)2

(9)

2 试验设备及方法

根据试验目的，设计了一种能够使测量探头在湍流场中移动的试验装置。试验设备分为两部分：①风洞，在此进行试验并产生湍流；②试验移动车辆系统，目标使探头能够以适当的速度平稳移动并进行湍流特性的测量。

2.1 风 洞

试验在西南交通大学风工程研究中心(RCWE)3号风洞(XNJD-3)中进行。该风洞是领域内最大的边界层风洞，其横截面为22.5 m(宽)×4.5 m(高)，工作段长度为36 m。极大的截面尺寸使探头能够以合适的速度在流场中移动。

空置风洞流速范围为1.0～16.5 m/s，湍流强度小于1.0%。大气边界层的被动模拟装置安装在试验部分入口的下游，由尖塔产生均匀水平各向同性的湍流。

2.2 移动列车试验系统

由驱动系统和数据采集系统组成的移动车辆试验系统由立柱支撑。立柱底部固定在风洞地面上。驱动系统由伺服电机、同步皮带和与皮带相连的滑块组成。4 kW伺服电机可为闭环驱动系统提供足够的动力，以在短距离内实现快速加速及减速。试验过程中，伺服电机驱动皮带运动，以驱动线性导轨上的滑块。为确保安全、稳定并平滑地测量，直线导轨由坚硬、平坦、轻质的铝合金制成。这也确保了滑轨运动时，滑轨的振动频率高于空气动力响应的振动频率。该仪器长20.5 m，高1.57 m，最大行进距离18 m，运行速度为0～15 m/s，加速及减速持续时间设置为0.5 s。此外，设计了随滑块移动的专用铝合金移动支架，用来连接下方轨道上的驱动机构和上方的TFI眼镜蛇探头。试验装置的示意图如图2所示。

图2 移动点风洞试验系统示意图Fig.2 Schematic diagram of moving point wind tunnel test system

为了显著提高测量系统的运行效率，使用计算机控制的数值系统来实现双向加速，减速和匀速运动。在短暂加速至设定速度后，滑块会经过稳定且均匀的运行阶段。显然，根据用户的判断手动控制试验，在给定的流速下，可以通过设置不同的移动速度来进行重复试验。为确保数据的连续性和有效性，采样在滑块移动开始之前开始，并在滑块移动停止几秒钟后结束。

测量探针采用TFI眼镜蛇三维脉动流速测量仪，其精度达±0.1 m/s。它是一种四孔压力探头，可实时测量动态的三分量速度和局部压力。眼镜蛇探头具有0～2 000 Hz的线性频率响应，有效风速范围为2～100 m/s。眼镜蛇探针的输入方向对应于来流方向。采样频率为512 Hz。此外应注意的是，因眼镜蛇探头有效测量范围(±45°)的限制，为确保数据的有效性，探头在横风方向移动时的移动速度不大于平均流速。根据本研究的目的和试验装置的设计，可获得在移动点上观测到的湍流脉动风速时程。

2.3 湍流特性模拟

准确模拟大气环境中的湍流风场是得到可靠风洞试验结果的前提条件。理论上风洞中由尖塔产生的湍流是水平及各向同性的，其统计特性与水平位置无关，仅随高度和时间而变化。为确保风洞模拟湍流的均匀性和各向同性，在测量高度沿导轨的线性路径的多个位置x/M对流场风参数进行了测量(x为测量点到起点的距离；M为线路总长)，流场湍流强度和积分尺度测量结果如图3所示，试验结果显示在同一高度下，流场的湍流强度和积分尺度接近，表明流场的均匀性良好。

图3 试验测量区域湍流强度及积分尺度横向分布Fig.3 Spanwise distributions of turbulence intensities and integral scales in the measurement region

测得的纵向、横向、竖向脉动风速湍流谱如图4所示，结果表明试验流场的风谱与von Kármán谱吻合良好，值得注意的是von Kármán谱可以良好的模拟大气边界层中的紊流流场，说明风洞中模拟的紊流场各向同性且与自然界流场吻合良好[18]。

图4 脉动湍流功率谱Fig.4 Power spectrum of fluctuating flow

此外，侧壁湍流边界层厚度均约为10 cm。因有效测量区域距离风洞侧壁较远(>5 m)，因此侧壁边界层效应的影响可以忽略不计。综上所述，风洞模拟的流场具有较好的品质，可以达到风洞试验的要求。

3 结果与讨论

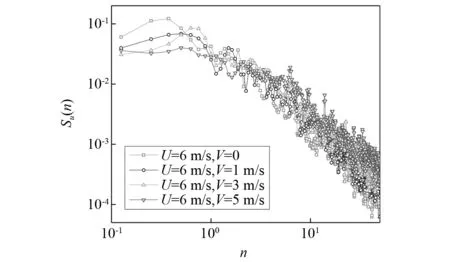
试验采样频率1 024 Hz。试验中使用了两组流速：U1=6 m/s；U2=8 m/s。通过改变运动速度V(V

3.1 湍流积分尺度

采用极坐标描述了在移动点处观察到的u分量积分尺度(Lu′)相对于速度夹角(β)变化的试验结果，用平滑曲线对结果进行了拟合，并基于试验点部分的拟合提出了如图5所示的半椭圆模型。从试验点或曲线到原点的距离为Lu′值。此外，将Balzer和Cooper谱模型中的湍流积分尺度也绘于图5中。

图5 移动点观测的u分量湍流积分尺度半椭圆模型Fig.5 Semi-elliptic model for the turbulence integral scale of the u-component observed at a moving point

根据上述结论及众多试验结果的拟合，基于椭圆公式提出了半椭圆模型的数学模型

(10)

将式(10)在极坐标系中表示

(11)

式中，a为常数，根据大量数据拟合，a≈5/6。

如上所述，随着给定流速下观察点移动速度的增加，u分量的湍流积分尺度不断减小。换句话说，湍流脉动中含能涡的平均尺寸减小了。然而，自然的湍流尺寸不会因外界条件的改变而变化，即湍流的长度尺度并未发生变化，该结果是因为测量的时间尺度随着V的增加而连续减小，即湍流时间尺度的变化致使运动点历经的湍流长度尺度的减小。

3.2 湍流脉动速度谱

将3.1节提出的湍流积分尺度半椭圆模型经验公式代入广泛应用的Cooper谱模型中，可得更新后的移动车辆历经的湍流脉动风速谱，将其与各工况下的试验结果进行比较。如图6所示，图6(a)所示的谱是固定点的测量结果，表示传统视角下的湍流脉动风速谱，可以严格地应用于不动结构的气动载荷和湍流脉动引起的响应。从移动点观测到的试验结果中，本文选取三组数据作为代表性结果进行频谱分析，如图6(b)、图6(c)、图6(d)所示，其中来流速度U=6 m/s，移动点速度V=1 m/s，V=3 m/s，V=5 m/s。

图6 移动点观测的u分量湍流脉动风速谱Fig.6 Turbulence spectra for the u-component observed at a moving point

由图6可以看出，基于半椭圆模型积分尺度的移动点湍流脉动风速谱与试验值拟合较好。而在具有不同运动速度观测点的结果之间，u分量的脉动速度谱是不同的。为了更清楚地显示这种差异，将不同移动速度下观测点测得的湍流脉动风速谱绘制在同一个图中，如图7所示。随着移动速度的增加，频谱总体上向高频移动。在高频区域中，在移动速度较大的点处观察到的频谱值大于在移动速度较低的点处观察到的频谱值，而在低频区域中则相反。随着移动点速度的增加，这种现象变得更加明显。另外，因频率和能量谱之间的转换关系(见式(4))，随着运动点速度的增加，运动车辆所历经的流动载荷能量(相对于波数)的变化与频谱具有相同的规律性。

图7 不同移动速度下u分量脉动速度谱试验值Fig.7 Experimental fluctuating velocity spectra for the u-component measured at different moving velocities

3.3 能量分布

湍流的总能量可以认为是气流中每个涡旋贡献的总和。对于各向均匀湍流的研究，为清楚地表示由不同速度的运动点测得的湍流的能量分布，这里用两波数风速谱对结果进行描述，如图8所示。

图8 移动点观测的u分量湍流能量分布Fig.8 Energy distribution of turbulence for the u-component observed at a moving point

图8(b)、图8(c)和图8(d)分别对应于移动点速度V=1 m/s，V=3 m/s，V=5 m/s的情况，同时，在固定点的观测结果示于图8(a)中以供参考。显然，随着观测点的移动，历经湍流的能量分布也随之变化。随着观测点速度与来流速度的比值增加，能量整体上将向高波数方向移动。高波数区域中能量占比持续增加，而低波数区域中的能量减小。可以预见，随着观测点速度的不断增大，高波数区域和低波数区域之间的能量差在整个波数区域中将持续缩小，直至极限为止，此时观测点的速度无限大，湍流特性可以忽略不计。

3.4 Doppler效应

从以上试验结果可以看出，在移动点观测的湍流脉动特性存在Doppler效应，这有助于定性理解高速车辆在随机流场中历经的脉动速度谱。

根据Doppler效应，波长因波源和观察点的相对运动而变化。运动导致波被压缩，波长变短，频率升高，进而引起了上述试验结果显示的湍流积分尺度和脉动速度谱的变化。在本文的研究中，观测点的移动速度直接影响来流与眼镜蛇探针之间的相对移动速度。观察点的速度越高，产生的Doppler效应越大，并且变化越显著。

另外，Lundsager等和Connell等也通过类似的运动报道了Doppler频移现象，即流速的旋转采样时间序列的频谱密度曲线不再符合传统频谱形状，表现为中频区域下降，而高频区域上升，叶片旋转速度与平均流速之比是移频过程中最重要的因素。他们的研究及本文研究表明，尽管湍流场特性保持不变，但观测点的运动(即参考系的变化)将引起湍流特性发生变化，如Doppler效应一样。

总之，测量方式不会改变湍流结构的实际尺寸和流速的空间变化(与参考系无关)，而仅因观测点的移动使得测量时湍流历经的持续时间变短。可以预见，当在运动参考系中观测湍流时，涉及时间和空间尺度的任何湍流特性都将改变，观测到的湍流频谱特性在几个子频率区域内失真，低频区域能量衰减，衰减的能量被分配到高频区域中。

4 结 论

本文旨在进行移动点湍流脉动特性的研究。为此设计了一种可使测量探针能够以平稳速度在流场中移动的试验设备。基于多次重复的测量及数据的分析研究，得出如下结论：

(1) 移动点历经的湍流脉动特性不同于固定点的观测结果。当常规的静止参考系变为运动参考系时，湍流速度时程是时间和空间位置的函数。结合先前在旋转参考系中观测的湍流特性的研究，可以认为湍流脉动特性的测量结果取决于观测参考系。

(2) 湍流u分量在来流纵向的积分尺度随着移动点速度与来流速度比值的增大而增大，Balzer积分尺度模型和Cooper谱模型基于的ESDU合成积分尺度模型在对其进行描述时存在一定的偏差，而本文提出的基于湍流积分尺度半椭圆模型得到的移动点历经的湍流脉动风速谱与试验结果吻合较好，具有较高的精度。

(3) 移动点历经的湍流谱能量由于运动而重新分布。随着观测点与来流的速度比增加，脉动速度谱整体向更高的频率偏移，能量向更高的波数区传递。并且某一固定来流风速下，随着观测点移动速度的增加，高频区域中的谱值增大，低频区域中的谱值减小。但湍流总能量不随观测点移动速度的改变而变化。

(4) 无论观察点是否移动，湍流u分量脉动速度均方根保持不变，且当来流风速恒定时，在不同速度的移动点处观测到的湍流强度不变。

(5) 移动点观测到的湍流脉动特性表现出明显的Doppler效应，根据试验结果推测，这很可能是由于移动点穿过涡流时湍流时间尺度的压缩引起的。

从工程学的角度来看，在移动点处测得的湍流特性构成了移动车辆的真实输入。本文研究方法及结果可为与移动车辆等历经的湍流特性提供有用的见解，为相应的工程应用做出有意义的贡献，同时为应对湍流中移动车辆的载荷及脉动风速引起的结构响应提供良好的基础，用于更好地评估横风下行驶车辆的舒适性和安全性等问题。