考虑油膜润滑的轮毂轴承弯曲疲劳寿命预测与分析*

林 棻 柴 靖 曹燕锋 杨东辉 臧利国

(1.南京航空航天大学能源与动力学院 江苏南京 210016；2.芜湖人本汽车轴承有限公司 安徽芜湖 241060；3.南京工程学院汽车与轨道交通学院 江苏南京 211167)

轴承是现代工业化社会中最常用的零部件之一，广泛应用于汽车、飞机、轮船等机械化设备当中。轴承在工作状态下会受到循环的应力作用，由于材料本身的特性，经过一段时间后逐渐会产生局部疲劳损伤，在轴承的滚动表面发生疲劳剥落而损坏，无法满足轴承的各项性能指标，达到了轴承的使用寿命极限。因此，准确地预测轴承的疲劳寿命具有十分重要的现实意义。

目前，轴承疲劳寿命模型主要有基于概率的工程模型和基于力学原理的理论模型。包括Lundberg-Palmgren模型、Ioannides-Harris模型、Zaretsky模型、Tallian模型。LUNDBERG和PALMGREN[1]在Hertz接触理论、Weibull材料强度统计理论和大量实验的基础上，创建了滚动疲劳最大动态剪应力理论并给出了相应的寿命计算公式。IOANNIDES和HARRIS[2]引入了局部应力和材料疲劳极限概念，认为当所受应力小于疲劳极限应力时，轴承材料不会发生疲劳失效。ZARETSKY等[3]提出了一种使用最大剪切应力准则的寿命预测模型。TALLIAN[4]综合了材料制造工艺、表面缺陷、污染状态等因素，对L-P理论进行了修正。

经典的L-P寿命理论作为轴承寿命分析的基础理论，国内外相当多的学者已进行了深入研究，并在此基础上提出了一些修正方法。卢光辉[5]提出了一个考虑残余应力和显微硬度影响的L-P修正模型，基于所建立的模型，分析了超精加工后的残余应力、显微硬度及离散度对疲劳裂纹的寿命影响。金燕等人[6]比较了ISO 2种寿命计算标准中计算方法和修正系数的差异，计算了航空圆柱滚子轴承的最小油膜厚度，确定了修正系数，分析验证了滚动轴承修正寿命结果。YAKOUT等[7]介绍了一种通过振动模态分析预测单个滚动轴承的疲劳寿命的实验方法,根据统计分析建立了一种将滚动轴承的动态负载能力与其动态特性(固有频率和阻尼)相关联的经验模型；根据滚动轴承的动态特性，提出了基于L-P寿命公式的修正公式。冷钢等人[8]建立了基于次表层最大剪应力的滚子轴承寿命修正模型，比较了与传统计算方法得到的寿命结果的差异。分析了径向力与弯矩、倾斜角、过盈量、温度对寿命的影响。

轴承的游隙影响载荷分布、摩擦、振动、温升和寿命等，是一项重要的技术参数。已有很多文献讨论了游隙的确定方法和影响因素。王学辉等[9]分析了工作游隙、过盈配合、温升、载荷引起的弹性变形4种影响轴承游隙的参数及各自计算方法，并通过实例计算验证了分析的正确性。郭攀成[10]定量地考虑了影响圆柱滚子轴承游隙的主要因素，提出了一种合理确定轴承径向游隙的计算方法，并总结出工作载荷会使轴承游隙增大的结论。孙春一和金世哲[11]提出了一种计算修正疲劳寿命的方法，直接用轴承的径向游隙值代替通过润滑理论计算的最小油膜厚度，进而求得修正系数，代入修正额定寿命公式，预测滚动轴承疲劳寿命。赵联春等[12]讨论了轴承润滑剂黏度比对寿命的影响，确定了在不同运行和加工条件下的计算方法。

影响轴承寿命最关键的因素就是轴承受到的外部载荷。获取轮毂轴承的载荷分布情况，有助于进一步分析疲劳寿命。 汪久根和徐鹤琴[13]考虑轴承运动特性，提出了一种载荷分布计算模型，分析了纯径向力作用下深沟球轴承的接触应力、载荷序列和疲劳寿命，讨论了载荷、游隙和离心力对深沟球寿命的影响，比较了不同运动状态下，2种寿命模型的计算结果。程超和汪久根[14]研究了双列角接触球轴承分别在径向载荷、中心轴向载荷、偏心轴向载荷和联合载荷作用下的载荷分布情况。讨论了最大载荷和接触角的变化规律。

对轮毂轴承的静力学分析中，已有相当多考虑径向载荷、轴向载荷或三力(径向、轴向、弯矩)联合载荷作用方面的研究，而对轮毂轴承受到纯弯矩载荷工况下的分析还比较少。因此，本文作者研究了纯弯矩载荷作用下轴承变形、接触应力和疲劳寿命的变化情况，结合L-P理论、Hertz接触理论、弹流润滑理论确定了一种疲劳寿命计算方法，考虑轴承游隙和油膜厚度的影响，提出了一种寿命修正方法。

1 轴承额定寿命

LUNDBERG和PALMGREN[1]提出的经典轴承寿命计算方法,随着使用材料和制造工艺的改善以及应用场景的不同，目前已进行了一些修正。国际化标准组织基于I-H寿命模型，在ISO 281—2007标准中给出如下的修正公式[15]:

LnM=a1aISOL10

(1)

式中：LnM是与可靠度对应的疲劳寿命；a1为可靠度寿命修正系数，值取1；aISO为轴承寿命修正系数。

aISO的值与润滑、环境、污染物颗粒、安装等影响因素有关，可通过如下公式[15]计算获得：

(2)

式中：CL为污染系数；Flim为疲劳载荷极限；κ为润滑剂黏度比；x1、x2和e1、e2、e3、e4可通过查表1获得。

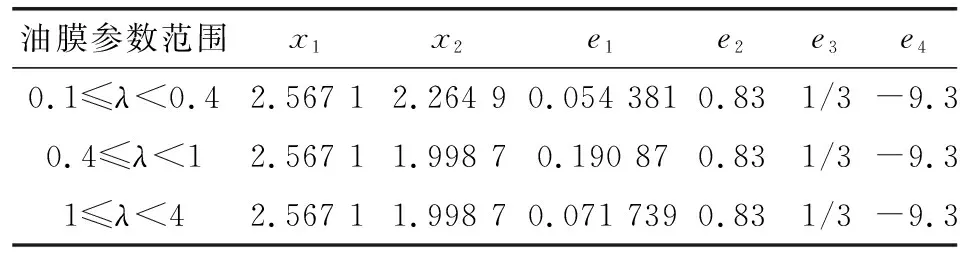
表1 式(2)中的常数和指数值

1.1 黏度比的确定

润滑剂黏度比κ

(3)

式中：ν为实际运动黏度；ν1为参考运动黏度。

同时，黏度比κ可通过油膜参数λ精确估算：

κ≈λ1.3

(4)

1.2 油膜参数的确定

油膜参数λ不仅受到油膜厚度的影响，还与接触表面粗糙度相关，其表达式[16]为

(5)

σ=1.25Ra

(6)

式中：σ1、σ2为两表面粗糙度的均方根偏差；hmin为最小油膜厚度；Ra为表面粗糙度。

轴承的润滑参数λ直接反映了润滑状态[16]，当λ≥3时，油膜完全隔开接触表面，称为全膜弹流润滑；当λ<3时，表面可能发生接触，称为部分膜弹流润滑；正常的滚动轴承工作状态下，λ的值在2左右；当λ≤1时，轴承将不能正常运转。

1.3 最小油膜厚度的确定

(7)

式中:Rx为沿钢球滚动方向的当量曲率半径；Qmax为最大滚动体载荷；m为椭圆率；αL为黏度压力指数；η0为常压下的动力黏度；u为表面平均速度；E0为当量弹性模数。

其中，表面平均速度为

(8)

(9)

式中：n为内圈或外圈转速；dm为节圆直径；γ为量纲一几何参数。

当量曲率半径Rx计算公式为

(10)

椭圆率可由下式计算：

(11)

(12)

式中：fj为内圈或外圈的沟曲率半径系数；R1为钢球半径；R2为套圈的沟曲率半径。

当量弹性模数E0表示为

(13)

式中：E1、E2、ξ1、ξ2为两材料的弹性模量和泊松比。

将式(10)—(12)代入式(7)得到钢球与内、外滚道的最小油膜厚度[16]为

(14)

综合考虑温升引起的游隙变动量、径向变形量、安装径向游隙、钢球与内、外滚道之间的最小油膜厚度、工作游隙之间的关系，得到总的油膜厚度为

(15)

式中：Δut为温升引起的游隙变动量；δθr为纯弯矩引起径向变形量；Gr为安装径向游隙；ur为径向工作游隙，取-0.011mm。

轴承在运转的过程中由于钢球与内、外滚道接触表面之间不是绝对光滑，存在摩擦现象，会导致轴承内部温度升高、零件体积膨胀，影响游隙和油膜厚度。由于温度对润滑剂的影响较为复杂，不同温度和压力下，黏度差异较大。但文中考虑的轴承温度变化较小，对润滑剂黏度影响可以忽略不计，故不考虑温度对润滑剂黏度的影响。

对于钢制轴承，温度升高引起游隙变动量的计算公式[16]为

Δut=ΔtαTdm

(16)

式中：Δt为内外圈的温度差，一般条件下Δt为5～10 ℃，若散热条件不好时，Δt可达15～20 ℃；αT为轴承钢的线膨胀系数，αT=1.25×10-5℃-1。

2 基本额定寿命计算

(1)额定寿命与额定滚动体载荷和实际滚动体载荷之间的关系[17]：

(17)

式中：Qc为额定滚动体负荷；Q为实际接触负荷。

(2)钢球与滚道的接触疲劳寿命为

(18)

式中：Qcξ为滚道受到的额定滚动体负荷；Qξ为滚道的实际接触负荷；ξ=i,o，ξ=i时，表示内滚道，ξ=o时，表示外滚道。

滚道基本额定动负荷[18]：

(19)

(20)

式中：fξ为内、外套圈的沟曲率系数；α为设计接触角。

(3)钢球与内外套圈的接触疲劳寿命为

(21)

式中：QBξ为钢球的基本额定滚动体负荷。

钢球-滚道接触时球的基本额定动载荷计算公式[17]为

(22)

式中：对球-外圈接触cξ=1，对球-内圈接触cξ=-1。

钢球在轴承旋转的过程中，既有自身旋转运动也有绕套圈旋转运动，而钢球寿命是以其自转的圈数计数，轴承寿命单位以旋转套圈的转数计数。忽略轴承的滑动转动，可得内圈每旋转一周钢球的转数为

(23)

钢球的疲劳寿命为

(24)

(4)结合轴承单列套圈、滚动体材料计算轴承整体寿命为

(25)

式中：Li、Lo为内外滚道材料寿命；LBi、LBo为滚动体材料寿命，可由式(23)、(24)计算得出。

(5)整套轮毂轴承寿命为

(26)

式中：k=1时，表示第一列轴承，k=2时，表示第二列轴承，指数e=10/9。

3 接触力学模型

在弯矩载荷作用下，内、外圈滚道产生的接触变形如图1所示，图2为轮毂轴承结构示意图[19]。

图1 轴承接触变形示意

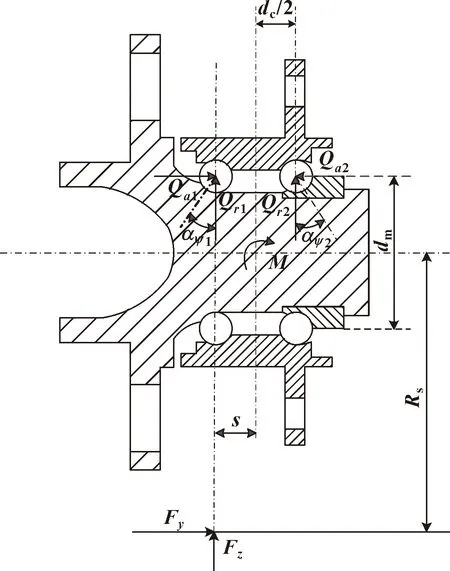
图2 轴承结构示意

轴承受载前任意位置内、外沟曲率中心距离为

A=(fi+fo-1)D

(27)

式中:fi、fo为内外滚道曲率半径系数；D为滚动体直径。

受载后产生接触变形，此时轴承内、外圈总的接触变形量为

(28)

受载后双列轴承内、外沟曲率中心距分别为

(29)

式中：α0为初始接触角；δθa为轴向位移分量；δθr为径向位移分量。

其中，由于接触变形引起的滚动体径向位移分量δθr、轴向位移分量δθa分别为

δθr=0.5dcθcosψ

(30)

δθa=Riθcosψ

(31)

Ri=0.5dm+(ri-0.5D)cosα0

(32)

式中:Ri为轴承中心与内圈沟曲率中心之间的距离；dc为两列钢球的中心距。

对于球轴承滚动体与滚道之间接触的载荷-位移关系，依据Hertz接触理论，有[16]:

Q=Knδ1.5

(33)

Kn=1/{[(1/Ki)1/n+(1/Ko)1/n]n}

(34)

(35)

(36)

式中:Kn为滚动体与内外圈之间总的负荷变形常数；η为两物体的综合弹性常数；∑ρ为接触点的主曲率和函数。

双列轴承第一列、第二列滚道任意位置接触变形量[19]分别为

(37)

将式(37)代入式(33)可得到法向接触载荷:

(38)

任意位置接触角αψ[16]可表示为

(39)

(40)

由法向接触载荷产生的轴向分量和径向分量为

Qak=Qψksinαψk

(41)

Qrk=Qψkcosψkcosαψk

(42)

可得到轴承的力矩平衡方程[19]：

(43)

使用牛顿迭代法[19]求解该方程，在MATLAB中编写计算程序，使计算结果满足精度要求。将计算结果θ代入式(41)、(42)可求得滚动体最大载荷。

4 试验验证

选取某型第三代轮毂轴承为研究对象，其具体结构参数如表2所示。

表2 轴承的结构性能参数

采用图3所示的旋转弯曲疲劳试验机进行多次疲劳试验[19]。将轮毂轴承外圈使用螺栓连接固定在试验台架上，内圈通过适配器与加载力臂相连接，电机带动上方的不平衡质量块，在旋转的过程中会产生离心作用，相当于对内圈部分施加一个旋转弯曲力矩作用，模拟轮毂轴承受力。当旋转频率的变化量大于初始频率的10%时判定试验结束，记录此时数据。

图3 旋转弯曲疲劳试验机

试验载荷：Q=M/L

试验弯矩：M=(μR-s)·F·t

式中：F为额定负载；t为强化系数，取1.8；μ为摩擦因数；R为车轮半径；s为车轮偏距；L为加载力臂长度。

设定加载循环次数106次，加载力臂长度L为0.685m，试验共进行3次，在旋转弯曲疲劳试验机上施加2.1kN·m的值，结果如表3所示。

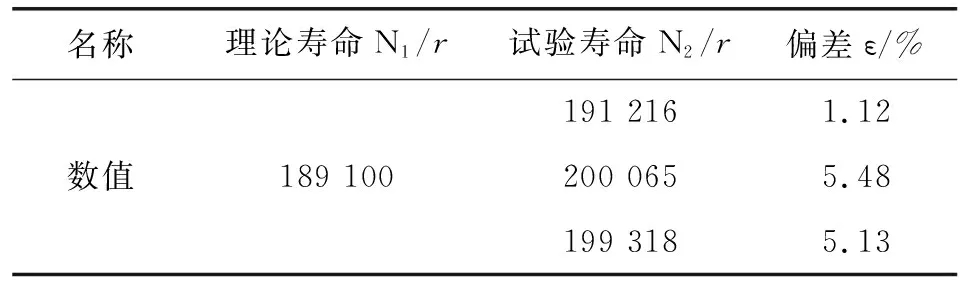
表3 弯矩2.1 kN·m下理论寿命与试验结果对比

对比试验数据和文中寿命模型预测的寿命值可知，理论预测值和试验值偏差在6%以内。证明文中建立的修正寿命模型具有一定的可靠性和实际参考价值。

5 仿真分析

轴承的载荷分布及大小直接与轴承应力相关，最终影响疲劳寿命。所以分析轴承的载荷分布情况，特别是确定最大滚动体载荷的研究十分重要。另外，轴承在运转过程中的摩擦与润滑也会受到载荷分布的影响。因此，要对轴承进行疲劳寿命分析，轴承的负荷分布方面的研究必不可少。

图4、图5所示为施加1.0kN·m弯矩载荷下，轮毂轴承第一列、第二列钢球的接触载荷随不同双列滚动体中心距的分布规律。可以看出：最大滚动体接触载荷随着中心距的增大而减小；在对应位置上，当第一列滚动体承受接触载荷值达到最大时，第二列滚动体达到最小。两列滚动体接触载荷变化趋势正好相反，大致呈对称分布；同时，当两列滚动体的中心距改变时，轴承的载荷分布变化并不明显，这说明中心距并不是影响载荷分布的主要因素。分析轴承的接触变形与中心距的关系，随着中心距增大，轴承变形量减小，结合公式(33)，载荷值随之减小。

图4 第一列滚动体载荷分布

图5 第二列滚动体载荷分布

6 轴承寿命影响因素分析

(1)不同滚动体中心距对轴承寿命的影响

利用文中建立的寿命模型计算不同两列滚动体中心距下的理论寿命值。图6所示为轴承寿命随中心距的变化规律。可以看出：弯矩一定时，随着中心距的增加，轴承寿命也在增加。同时，施加不同的弯矩，对寿命也有影响。在同一两列滚动体中心距下，随着弯矩载荷M的增加，轴承寿命开始减小。弯矩载荷增大，则根据牛顿迭代法计算的角位移增大，因而轴承受到的滚动体载荷也增加，轴承寿命减小。当轴承受到的弯矩较小时，中心距对寿命的影响较为显著；随着弯矩增大，这种影响逐渐减弱。

图6 不同弯矩下中心距与疲劳寿命的关系

图4、5中的结果表明，两列滚动体中心距会影响轴承的最大滚动体载荷，导致疲劳寿命发生变化，与图6中的结果一致。

但是，两列滚动体中心距与轮毂轴承的结构相关，直接影响其几何形状。因此，在空间允许的情况下，出于成本和制造工艺等多方面考虑，适当增加中心距可以延长轴承寿命。

(2)车速对轴承寿命的影响

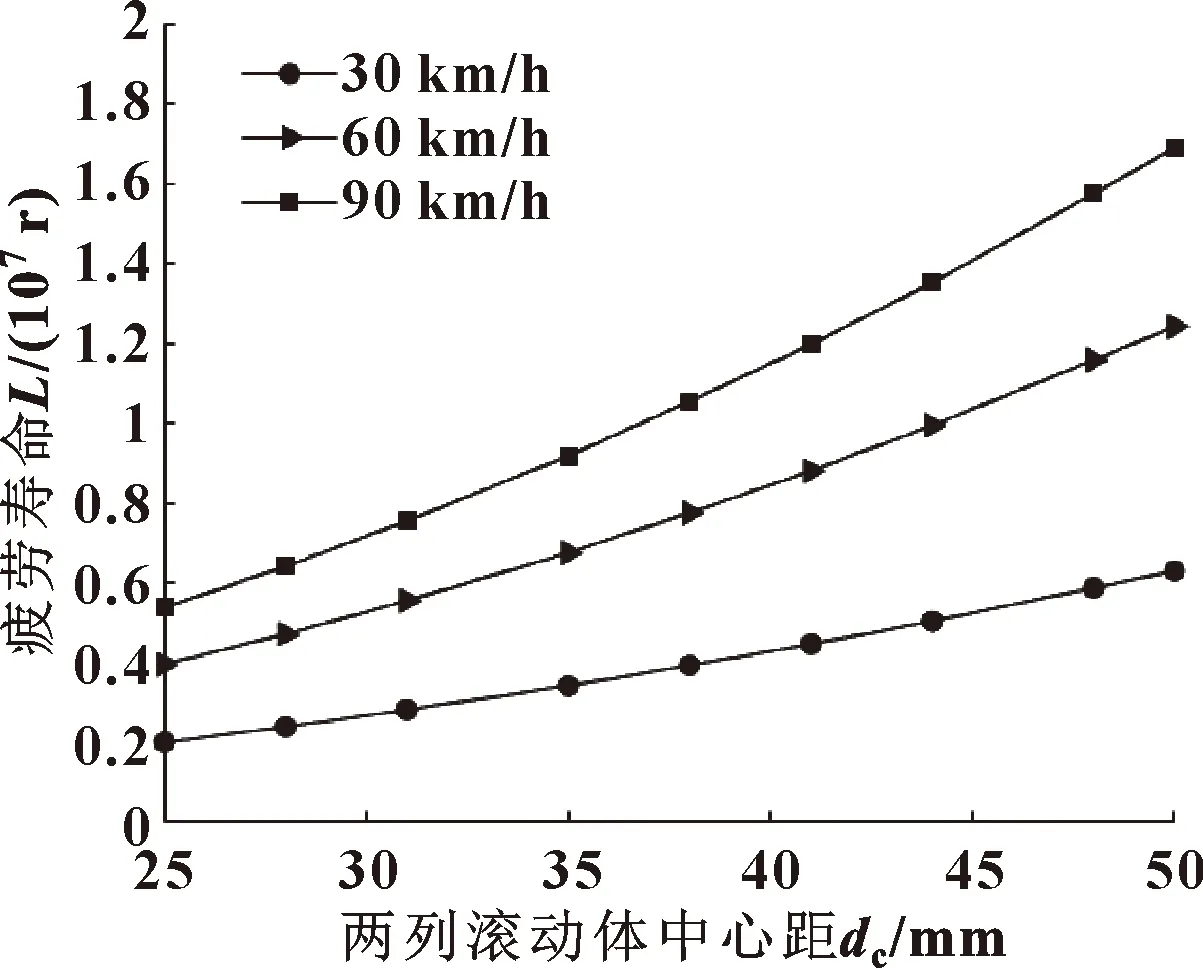
图7 不同车速下中心距与疲劳寿命的关系

7 结论

(1)考虑温度对游隙的影响，结合轴向变形量以及工作游隙，在道森-希金森公式的基础上，确定了最小油膜厚度值；然后计算出修正系数aISO，套用滚动轴承寿命计算公式，计算修正后的轮毂轴承疲劳寿命，使结果更加可靠。使用弯曲疲劳试验机验证了文中理论寿命模型的正确性，结果误差为6%，位于合理区间内，为下一步疲劳寿命分析提供了基础。

(2)分析施加纯弯矩载荷作用下，两列滚动体中心距对寿命影响的变化规律。结果表明：弯矩对轮毂轴承疲劳寿命影响显著，弯矩载荷越大，寿命值越低；轴承寿命随着双列滚动体中心距的增大而增大；在中低速工况下，轴承转速越高，润滑情况越良好，疲劳寿命相应增加。