一类有限非链环上的循环码及其Gray映射
钟家伟
(安徽信息工程学院 通识教育与外国语学院,芜湖 241000)
有限环上的循环码因其生成矩阵形式较为简单,编码译码方面容易实现,因此在数字通信中得到广泛的应用,是一类重要的线性码。有限环上的循环码目前被广泛的应用于代数编码的理论中,并且取得了瞩目的成就。近年来,随着通信技术对编码要求的提升,编码理论的研究从有限链环上码的研究延伸至有限非链环上码的研究,构造出了许多参数接近各种界的最优码。BETSUMIYA K 和 ZHU 等人[1-2]对环F2+vF2上的线性码与循环码进行了研究。ZHU等人随后在文献[3]中将相关结论推广至环Fp+vFp(v2=v)上,得到环上的(1-2v)常循环码的构造方法。YILDIZ B等人[4-6]对环F2+vF2+uF2+uvF2上的循环码和自对偶码的相关结构和性质进行了研究。文献[7-8]分别介绍了环F2+vF2+uF2+uvF2上两类常循环码的结构,并通过所构造的Gray映射得到了一系列最优码和渐进优码。文献[9]研究Fp+vFp+uFp+uvFp上的Gray映射得到其上一类常循环码。近年来,有限非链环的研究取得了许多成果[10-12],文献[13]介绍了利用环Fp+uFp+u2Fp+vFp+uvFp+u2vFp+v2Fp+uv2Fp+u2v2FP的λ-常循环码得出一类构造量子码的方法。
为了能够得出更多符合现代通信技术需求的具有良好参数的最优码,首先通过计算给出了环F2+uF2+vF2+uvF2上极大理想,研究了环F2+uF2+vF2+uvF2上循环码的结构。定义了环F2+uF2+vF2+uvF2上码长为n的循环码到二元域上长为4n的准循环码的Gray映射,并证明其保距性。研究得出此类环上循环码存在的充要条件,最后举例说明一类二元准循环最优码的构造方法。
1 环ℜ上线性码
令环 ℜ =F2+uF2+vF2+uvF2,其中u2=0,v2=v,uv=vu,R=F2+uF2,则可知ℜ=R[v]/(v2-v)。计算得出ℜ的理想:

可知ℜ是一个有限非链环,故ℜ不是局部环,ℜ的极大理想为(u+v)和(1+u+v)。
令C是ℜ上长为n的码字,即为ℜn的一个子集。若C是ℜn的一个ℜ-子模,则称C为ℜ上长为n的线性码。记ℜ∗为ℜ的非零子集,给定任意λ∈R∗,定义ℜ上的λ-循环移位为σλ(x0,x1,…,xn-1)=(λxn-1,x0,…,xn-2)。当λ=1时,有σ(C)=C成立,则称C为ℜ上的循环码。C上的码字c=(c0,c1,…,cn-1)可以等价表示为n-1次多项式c(x)=c0+c1x+ … +cn-1xn-1,则ℜ上长为n的码等价于商环ℜ[x]/(xn-1)的多项式,xc(x)为c(x)在ℜ[x]/(xn-1)中的一个循环移位。ℜ可以看作R上的向量空间,ℜ上长为n的循环码是环ℜ[x]/(xn-1)的一个理想。
2 环ℜ上的循环码
定义2.1 对于ℜ上任意长为n的码字x=(x0,x1,…,xn-1) ∈ ℜn,其中xi=ri+vqi,0 ≤i≤n-1,ri,qi∈R。ℜ上任意长为n的线性码到R上长为2n的线性码的Gray映射为:
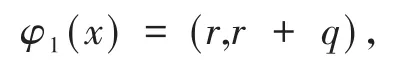
其中,r=(r0,r1,…,rn-1),q=(q0,q1,…,qn-1)。
引理2.2[2]令C是ℜ上长为n的线性码,
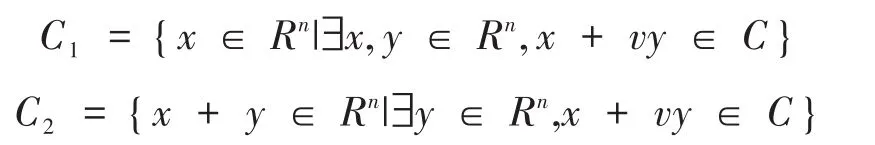
易知C1和C2也是R上的线性码,根据中国剩余定理可得:

定理2.3 ℜn上的线性码C=(1+v)C1⊕vC2是循环码,当且仅当C1和C2均是R上长为n的循环码。
证明:令C是ℜ上长为n的循环码,σ(c)=(cn-1,c0,…,cn-2)为c的一个循环移位,取任意c=(c0,c1,…,cn-1) ∈C,其中ci=ri+vqi,ri,qi∈R,0≤i≤n-1。则σ(c)=σ(r)+vσ(q)=(1+v)σ(r)+v(σ(r)+σ(q))。不妨设r=(r0,r1,…,rn-1)∈C1,q=(q0,q1,…,qn-1)∈C2,则σ(r) ∈C1,σ(q)∈C2,得出C1和C2都是R上长为n的循环码。
若C1和C2为R上长为n的循环码,取r=(r0,r1,…,rn-1) ∈C1,q=(q0,q1,…,qn-1) ∈C2,则r+q∈C2,假设ci=ri+vqi,0≤i≤n-1。由于C1和C2都是R上长为n的循环码,则有σ(r)∈C1,σ(r+q)∈C2。对于c=(c0,c1,…,cn-1),有σ(c)=(1+v)σ(r)+v(σ(r)+σ(q))∈C。得出C是ℜ上的循环码。
引理 2.4[14]设C是F2+uF2上长为n的循环码,其中n≡ 1(mod2),则存在唯一的f、g、h使得:
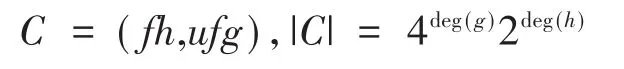
其中,f、g、h∈F2[x]为首一多项式,且xn-1=fgh。
令 ℜn[x]=ℜ[x]/(xn-1),多项式f∈F2[x]的互反多项式记作f∗(x)=xkc(x-1),下面研究得出ℜ上长为n的循环码的生成多项式,其中n≡ 1(mod2)。
定理2.5设C为ℜ上长为n的循环码,其中n≡ 1(mod2),则存在唯一多项式fi、gi、hi,i=1,2,使得:
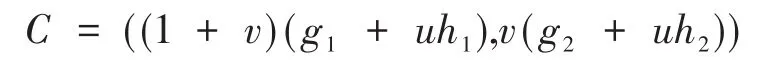
其中,f1g1h1=f2g2h2=xn-1为首一多项式。
证明:由引理2.2知ℜ上任一循环码C可表示为C=(1+v)C1⊕vC2,由引理2.4可得C1=(g1+uh1),C2=(g2+uh2),其中f1g1h1=f2g2h2=xn-1。取C中任意的码字多项式:
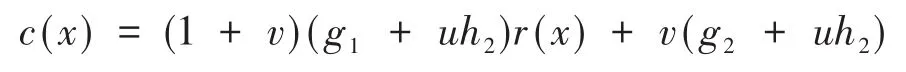
其 中,r(x)、q(x)∈Rn[x]。显 然,C⊆ ((1+v)(g1+uh1),v(g2+uh2))。
多项式((1+v)(g1+uh1),v(g2+uh2))上任意元素根据引理2.2可表示为:

其中,k1(x)、k2(x) ∈Rn[x]。故必然存在r(x)、q(x) ∈Rn[x],使得:

因此,((1+v)(g1+uh1),v(g2+uh2))⊆C,
综上可知C=((1+v)(g1+uh1),v(g2+uh2))。
定理2.6 设C=(1+v)C1⊕vC2为ℜ上长为n的循环码,其中n≡ 1(mod2),则有:
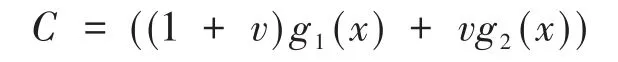
其中,g1(x)是C1的生成多项式;g2(x)是C2的生成多项式。
证明:令g(x)=(1+v)g1(x)+vg2(x),其中g1(x)是C1的生成多项式,g2(x)是C2的生成多项式。由定理2.2可知,若C为ℜ上长为n的循环码,其中n≡ 1(mod2),则有C=((1+v)g1(x),vg2(x)),显然(g(x)) ⊆C。
由 (1+v)g1(x)=(1+v)g(x),vg2(x)=vg(x),可得C⊆(g(x))。
综上,可得C=(1+v)g1(x)+vg2(x)。
根据文献[13],结合定理2.6,易得以下推论:
推论 2.7 若n≡ 1(mod2),则环 ℜn[x]是一个主理想环。
ℜ上线性码C的对偶码定义为:

推论2.8 设C为ℜ上长为n的循环码,n≡ 1(mod2),则C⊥也为ℜ上循环码。
设多项式e(x)∈ℜn[x]是循环码的生成多项式,满足e2(x)=e(x),则称e(x)为环 ℜn[x]的幂等生成元。
定理2.9 设C=(1+v)C1⊕vC2为ℜ上长为n的循环码,n≡ 1(mod2),则存在幂等生成元e(x)=(1+v)e1(x)+ve2(x),满足C=(e(x))。其中,e1(x)是C1(x)的幂等生成元,e2(x)是C2(x)的幂等生成元,并且幂等生成元e(x)是唯一。
证明:由e1(x)是C1(x)的幂等生成元,e2(x)是C2(x)的幂等生成元,记e(x)=(1+v)e1(x)+ve2(x),根据定理 2.9可知,C=((1+v)e1(x)+ve2(x))。由e(x)2=((1+v)e1(x)+ve2(x))2=(1+v)e1(x)+ve2(x)=e(x),知e(x)是码C的幂等生成元。若定义e′(x)是码C的另一幂等元,显然e′(x) ⊆e(x)。
另一方面,设e′(x)=m(x)e(x),则e(x)=e′(x)e(x)=m(x)e(x)e(x)=me(x)e′(x),反 之,同理可知e′(x)e(x)=e(x)。综上可得e′(x)=e(x),即码C的幂等生成元是唯一。
下面研究了环ℜ上循环码的对偶码的幂等生成元。
定理2.10 设C=(e(x))为ℜ上长为n的循环码,n≡ 1(mod2),其中e(x)为循环码C的幂等生成元,则1-e(x-1)为C的对偶码C⊥的幂等生成元。
证明:假设C=(1+v)C1⊕vC2,e1(x)是C1(x)的幂等生成元,e2(x)是C2(x)的幂等生成元。由定理2.3得C1(x)、C2(x)为ℜ上的循环码,由定理 2.9 可得e1(x-1)、e2(x-1)分别为C1、C2的幂等生成元。由推论2.8可知,C⊥也为ℜ上循环码,故对C⊥也可通过C⊥=(1+v)C1⊥⊕vC2⊥进行表示,因为(1+v)(1-e1(x-1))+v(1-e2(x-1))=1-e(x-1),故C⊥的幂等生成元可表示为1-e(x-1)。
3 环ℜ上的Gray映射
纠错码的重量和距离作为两个重要参数,是衡量是否为优码的重要指标。首先定义环ℜ上元素的Lee重量,具体如下:
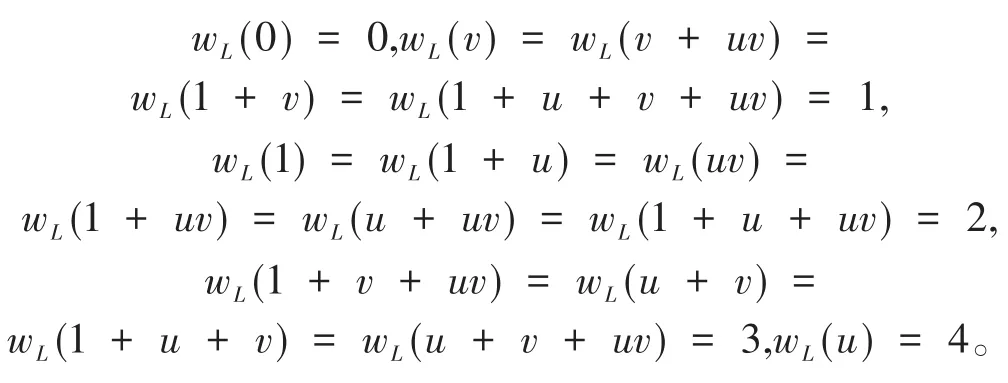
对于环ℜ上任意长为n的码字c=(c0,c1,…,cn-1),定义c的 Lee重量为:

定义 3.1[14]环R=F2+uF2上线性码的 Lee重量为:
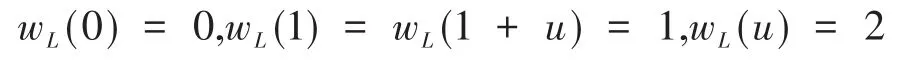
R到F2的映射:

Rn到F22n的保距映射:
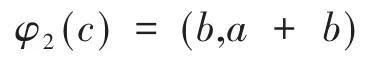
其 中,c=(a0+ub0,a1+ub1,…,an-1+ubn-1);a=(a0,a1,…,an-1);b=(b0,b1,…,bn-1)。
通过定义2.1中所定义的ℜn到R2n的映射φ1和定义3.1中Rn到F22n的映射φ2,首先定义 ℜn上Lee距离到F24n上Hamming距离的保距映射φ,然后证明其为保距映射。
定义3.2 定义(ℜ,Lee距 离)到(F42,Hamming距离)的映射θ:
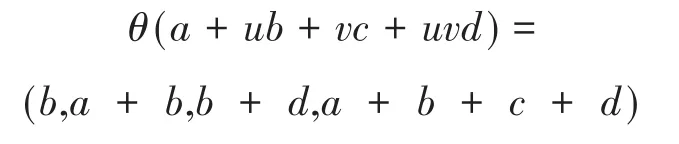
其中,a、b、c、d∈F2。
(ℜn,Lee距离)到(F4n2,Hamming距离)的Gray映射φ:

定义3.3 设C为环ℜ上长为n的线性码,φ(C)为码C的Gray映射,码C的Lee距离为:

φ(C)的Hamming距离为:
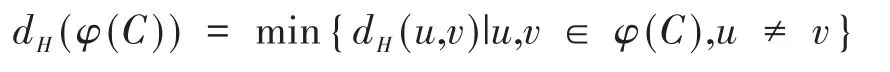
推论 3.4(ℜ,Lee距离)到(F24,Ham ming距离)的Gray映射φ是保距映射。
推论3.5 设C为ℜ上长为n的线性码,则φ(C)为二元域上长为4n的线性码。
推论3.6 设C为ℜ上长为n的循环码,n≡ 1(mod2),则有:
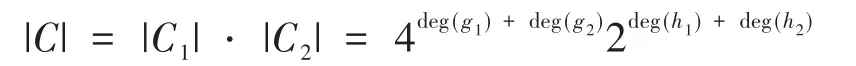
其中,f1g1h1=f2g2h2=xn-1。
定理3.7设C为ℜ上长为n的线性码,则其对偶码满足φ(C⊥)=φ(C)⊥。
证明:令:
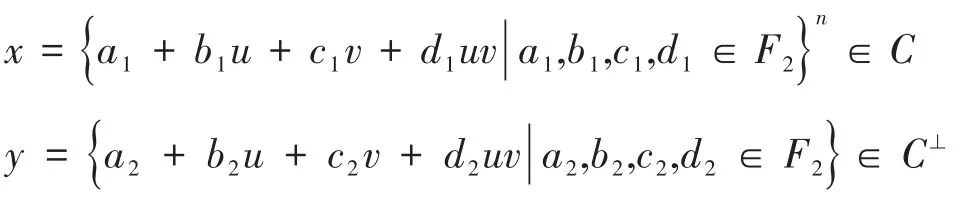
根据对偶码的定义有x·y=0,故:

由上式可得:

故φ(C⊥) ⊆φ(C)⊥。
反之,易知φ是双射,故有|φ(C)|=|C|和|φ(C⊥)|=|C⊥|成立,有|C|·|C⊥|=42n成立,得到|φ(C)|·|φ(C⊥)|=24n。根据推论3.6,不妨假设|C|= 4k12k2,则 |φ(C)|=|C|=4k12k2,|φ(C⊥)|=|C⊥|= 24n-2k1-k2,故 |φ(C⊥)|=|φ(C⊥)|。
综上可得,φ(C⊥)=φ(C)⊥。
根据定义3.2中所构造的环ℜn到域映射,对于任意的ℜn上的循环码的码字c=(c0,c1,…,cn-1),定义上的准循环移位ψs为:
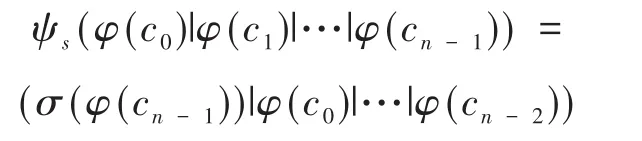
定理3.8 设C为ℜ上长为n的循环码,则φ(C)为二元域上长为4n的循环码。
定理3.9 设ℜ上长为n的循环码C=(1+v)C1⊕vC2,n≡ 1(mod2),则C极小 Lee距离满足:
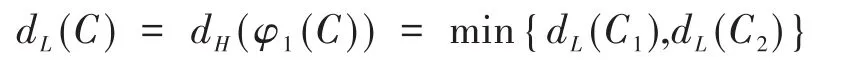
其中,dL(C1)是C1的极小 Lee距离;dL(C2)是C2的极小Lee距离。
证明:由C=(1+v)C1⊕vC2,其中C1、C2为R上的循环码,对应码C生成矩阵可以表示为:
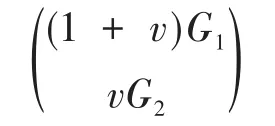
其中,G1为C1的生成矩阵;G2为C2的生成矩阵。易知φ1(C)的生成矩阵可以为:

根据矩阵的结构特点,得:

利用定理3.9,结合ℜ上循环码的结构特点,通过ℜ上循环码的二元Gray象φ(C)可构造一些参数较好的极小Hamming距离二元最优码或渐进优码。
4 应用举例
例4.1当n=3时,在二元域上中对x3-1进行因式分解可得:
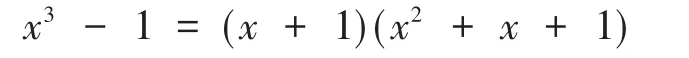
对于ℜ循环码C=(1+v)C1⊕vC2,取:
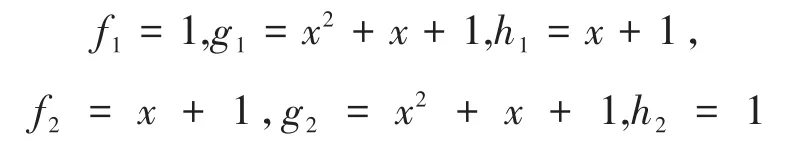
则可得φ1(C1)参数为[6,422,2],φ1(C2)的参数为[6,42,2]。根据定理3.9可得二元域上的Lee距离dL(φ(C))=2,故所构造的二元域上的准循环码φ(C)参数为[12,9,2]二元准循环最优码。
例4.2 当n=7时,在F2中对x7-1进行分解可得:
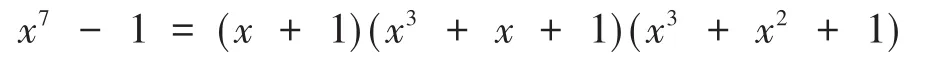
对于C是ℜ循环码,取:
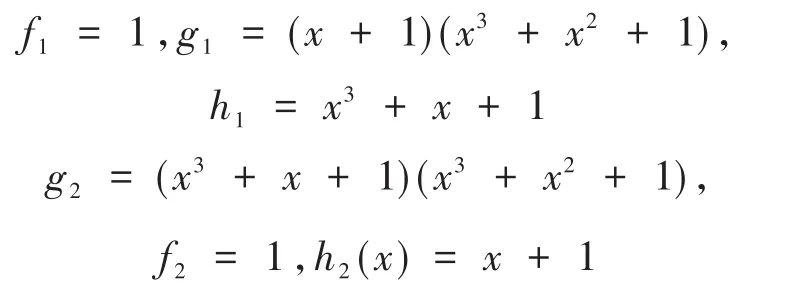
则可得φ1(C1)参数为 [14,4423,2],φ1(C2)的参数为[14,462,2]。根据定理3.9可得二元域上的Lee距离dL(φ(C))=2,所得的码C的 Gray二元象φ(C)是[28,24,2]二元准循环最优码。
5 结论
为了更加全面的了解有限非链环的结构性质,并构造一些二元域上最优码或渐近优码,更好解决通信中的纠错问题,首先对环F2+vF2+uF2+uvF2上的循环码的结构特征进行研究,得出其生成多项式和幂等生成元.进一步说明了环F2+vF2+uF2+uvF2上的循环码结构具有较易编译的特点。构造了从环上的循环码到二元域上准循环码的Gray映射,证得其保距性,并同步证明了其对偶码也是循环码的结论,为后续构造具有极小距离的最优码提供了理论依据。通过循环码的结构特点得出较好的极小Hamming距离二元最优码或渐进优码。今后还可持续研究环F2+vF2+uF2+uvF2上的常循环码、自正交码和量子码的结构及其重量分布、覆盖半径、周期分布等相关性质。

