基于元胞自动机的COVID-19传播动力学研究
施思远,蔡朝瑞,杜宝良,周林华,孟品超
(长春理工大学 数学与统计学院,长春 130022)
如今,COVID-19对公共社会卫生安全造成了严重的危害,人们迫切需要对COVID-19展开更全面的研究[1],从而制定最佳的防控疫情策略。在20年2月初,一艘由日本横滨出发的“钻石公主号”邮轮成为了COVID-19大规模爆发的重灾区,在全员人数仅仅3 700多名的情况下,感染人数达到了621例,近16%的人感染。
在过去的一年里,研究学者们主要基于SEIR模型对传染病传播动力学进行研究。张宇[2]针对交通工具内部空间狭小、乘客之间接触率高等特点对SEIR型进行改进,建立交通工具内部新冠肺炎疫情的传播模型。Wu Joseph T[3]基于人口流动性对SEIR模型进行改进,对人口流动性大的城市进行新冠肺炎病例数量预测。邱小[4]基于SEIR模型对地铁传染病传播进行仿真预测,得到了较为可靠的传染率参数。李眩[5]基于元胞自动机建立传染病传播和控制仿真模型,验证不同疾病致死率对疫情传播的影响。畅春玲[6]通过建立具有垂直传播和一般接触的元胞自动机传染病模型来研究不同传播方式对疫情传播的影响。Salathé M,Kazandjieva M[7]基于元胞自动机模型,从行人出行交通方面出发,探究其对疫情扩散程度的影响。
总体而言,目前对于传染病传播动力学研究主要停留在传统微分方程SEIR模型或是基于元胞自动机的传染病传播模型上,前者是从宏观的角度考虑传染病传播,对于人与人之间的接触和人本身运动的随机性无法考虑到位,后者是从微观角度考虑传染病传播,未考虑人员行走路径多样化的问题,只是简单地从疾病扩散角度出发进行研究。本文以“钻石公主号”邮轮为例,针对其具有复杂密闭环境和人员行走路径多样化的特点,分别制定了传染病传播演化规则、行人避让规则以及移动规则,基于上述规则进行模拟仿真实验,并通过设置隔离措施、限制人员出行和提高人员防护措施三个角度进行实验,得出有效合理的疫情防控策略。
1 基于元胞自动机的传染病传播模型
1.1 元胞自动机模型原理
元胞自动机(Cellular Automatio,CA)是一个空间、时间和状态均离散且状态随时间不断发生变化的动力学系统[8],由元胞的空间构型、元胞状态、邻居和元胞演化规则组成。每一个元胞自动机系统可以描述为一个四元组:

其中,Ld表示空间构型为d维,空间大小为L×L的网格空间;S表示元胞空间状态集合;N表示以某一元胞为中心的所有元胞组合;f表示元胞状态演化规则函数的集合。
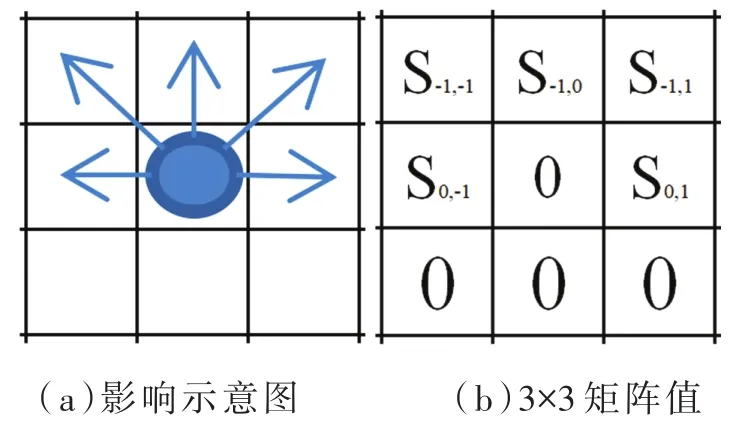
本文采用Moore型元胞邻域,如图1所示。

图1 Moore型元胞邻域
1.2 传染病传播演化规则
元胞演化规则函数f是一个状态转移函数:

模型仿真过程,在t时刻第i个个体的状态空间S有以下4种取值:
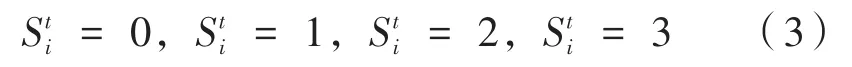
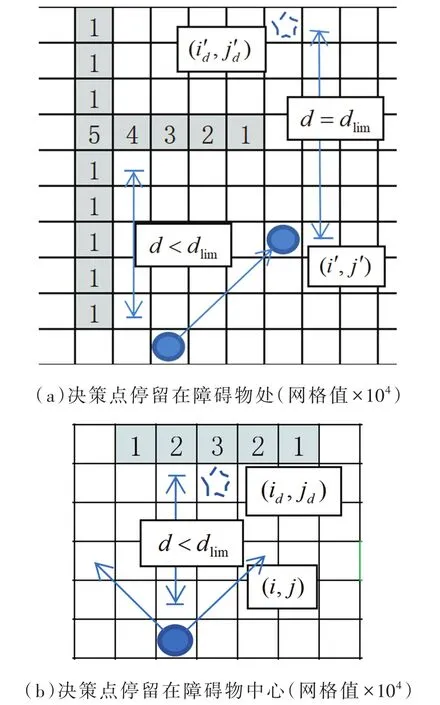
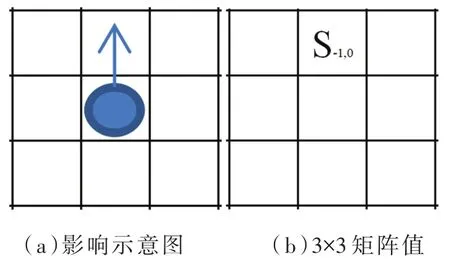
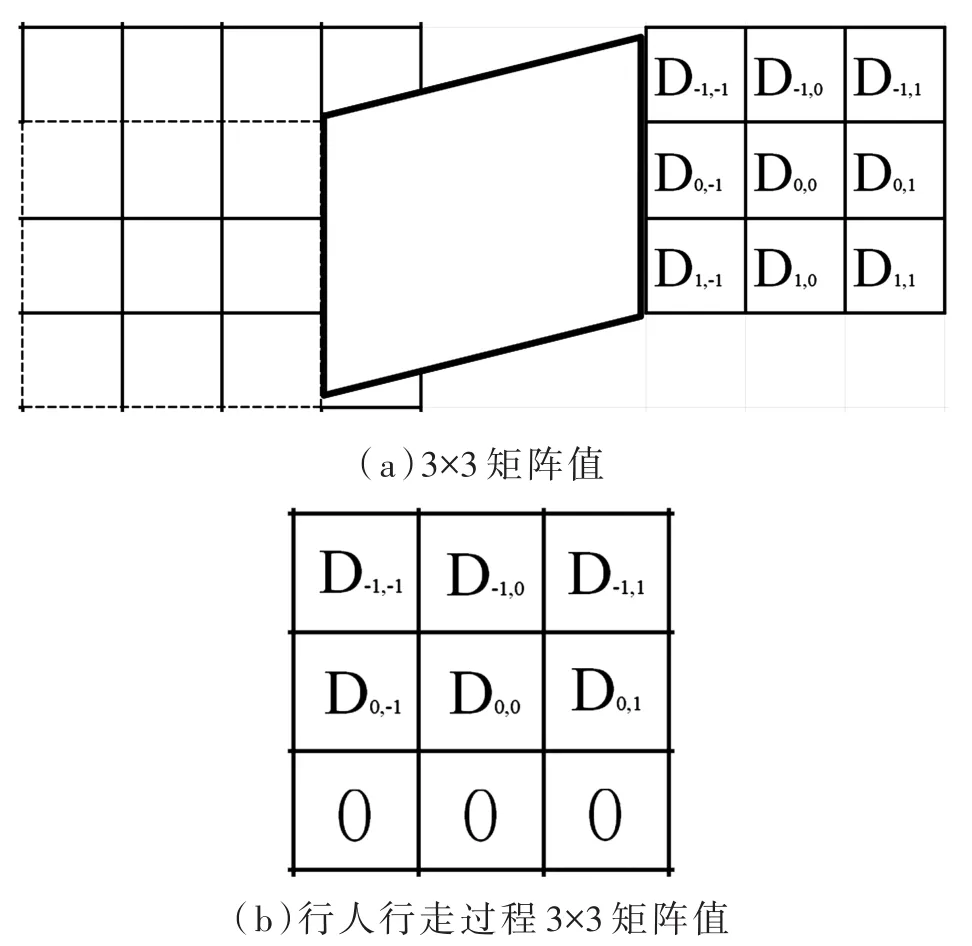
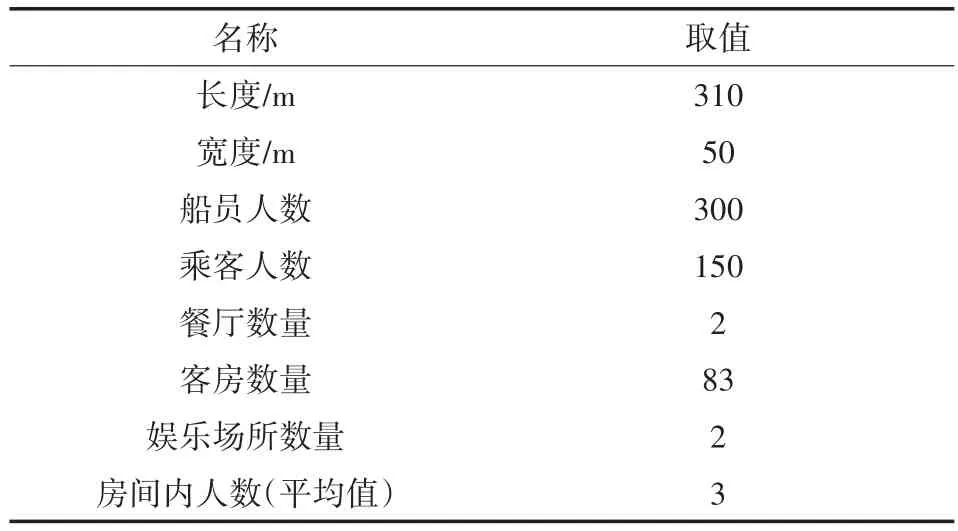
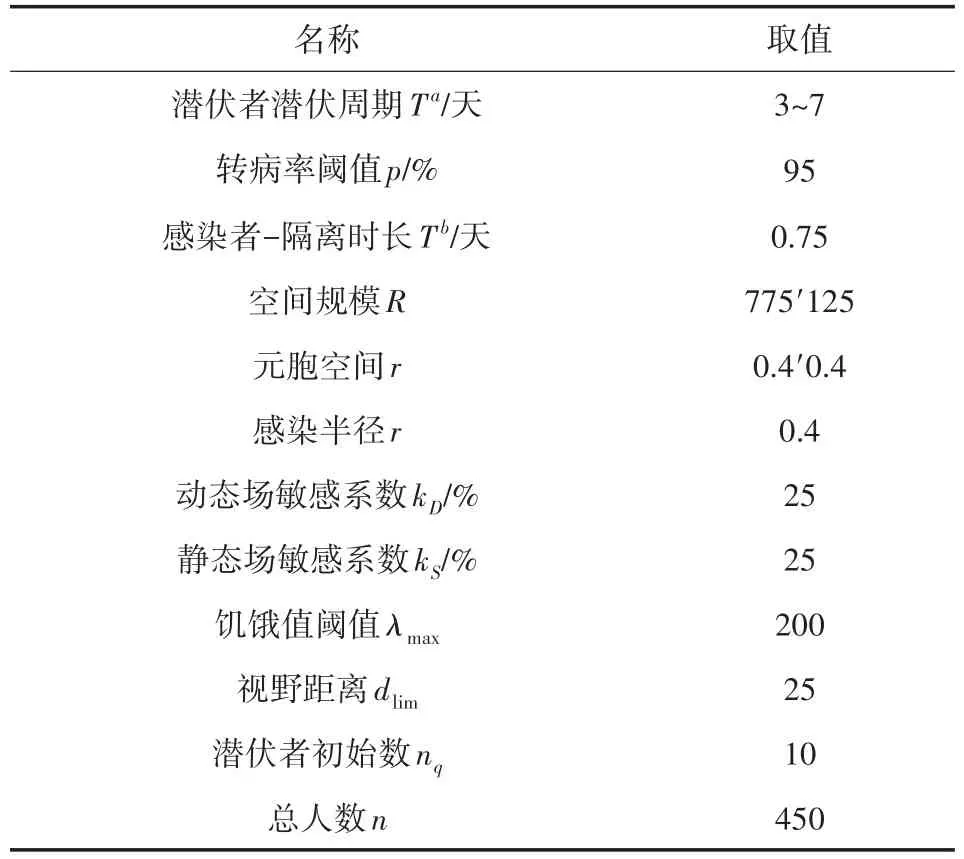
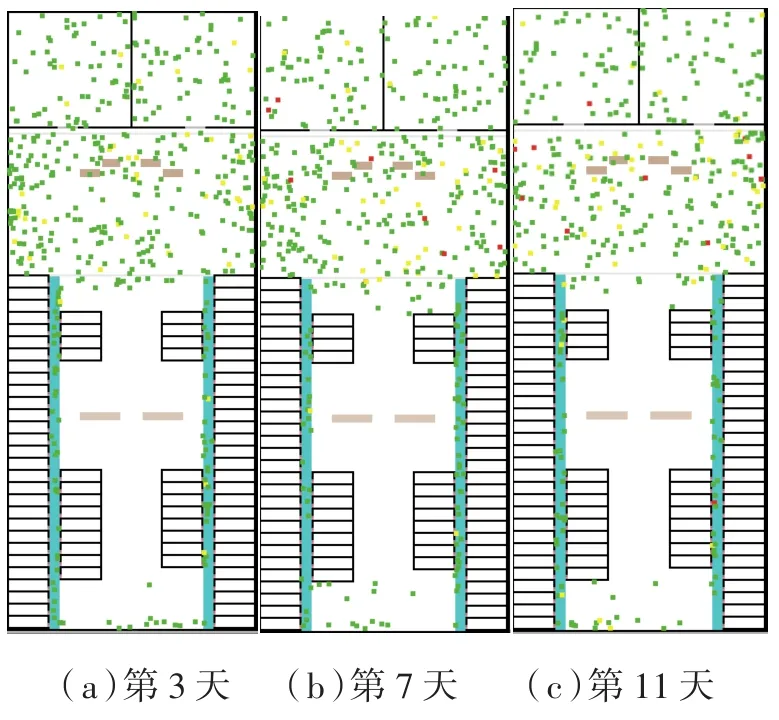
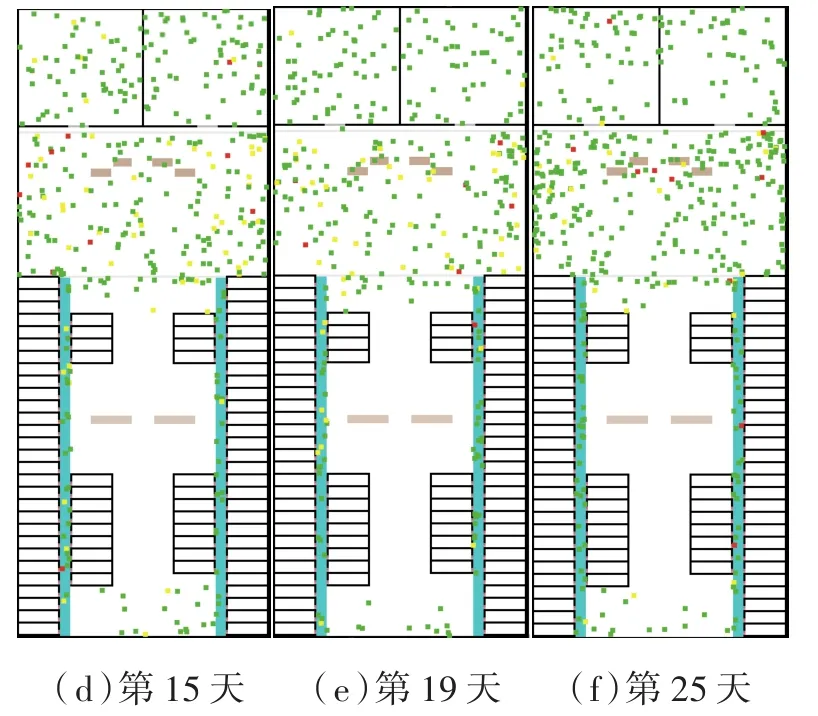
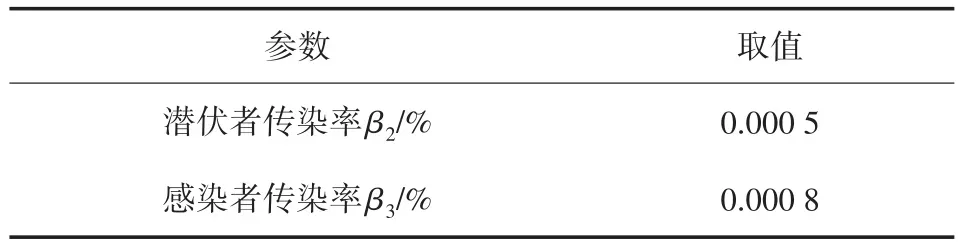
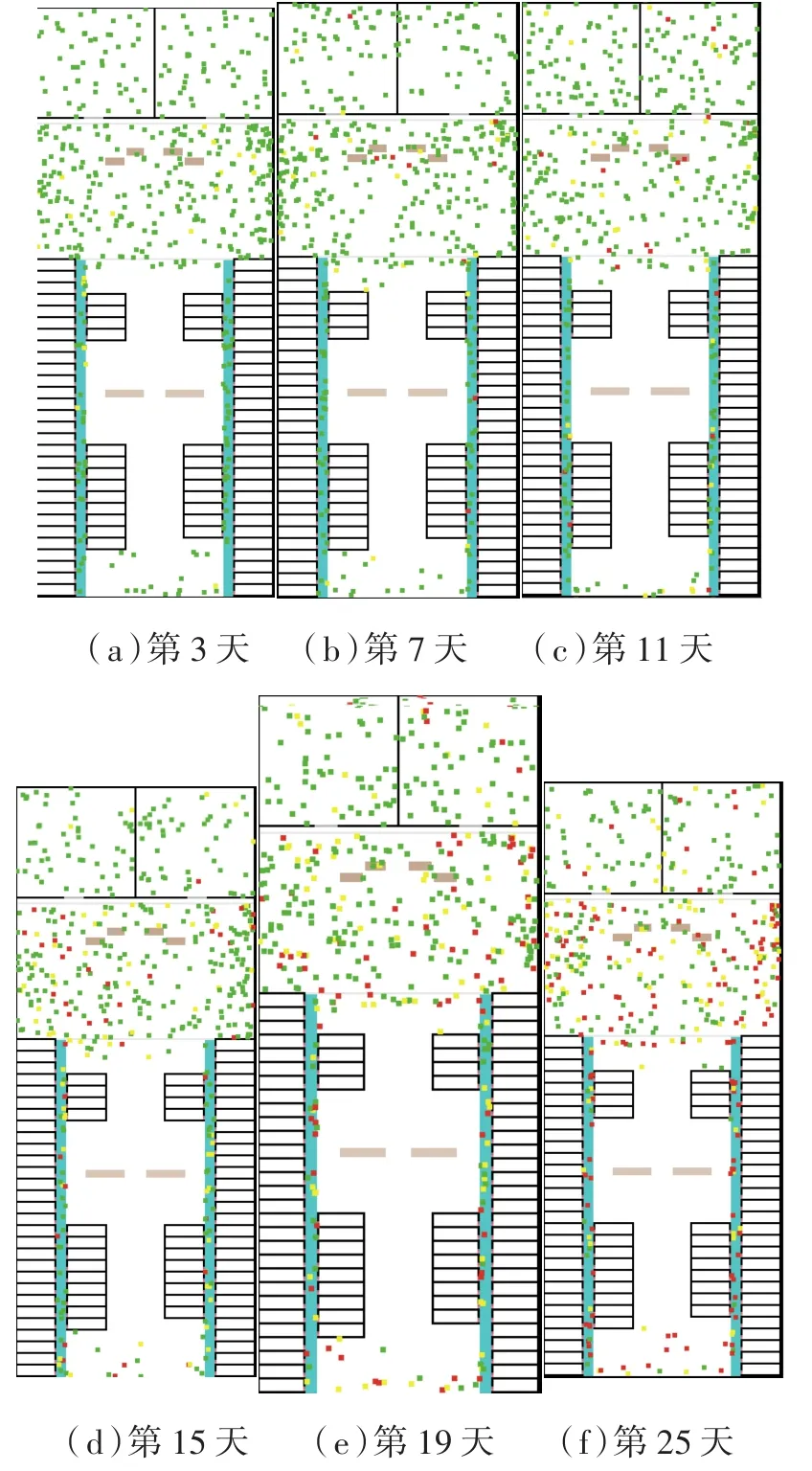
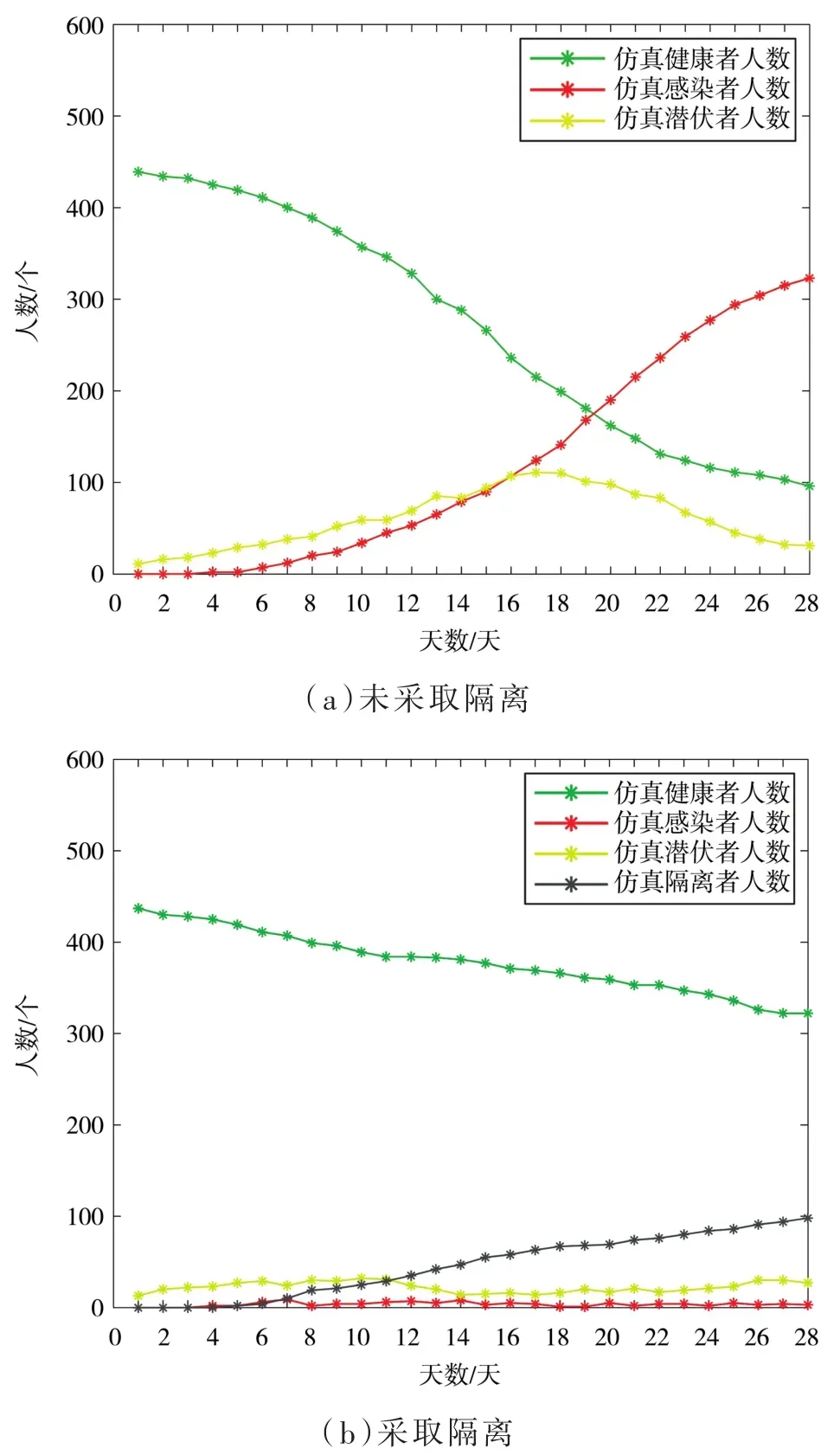
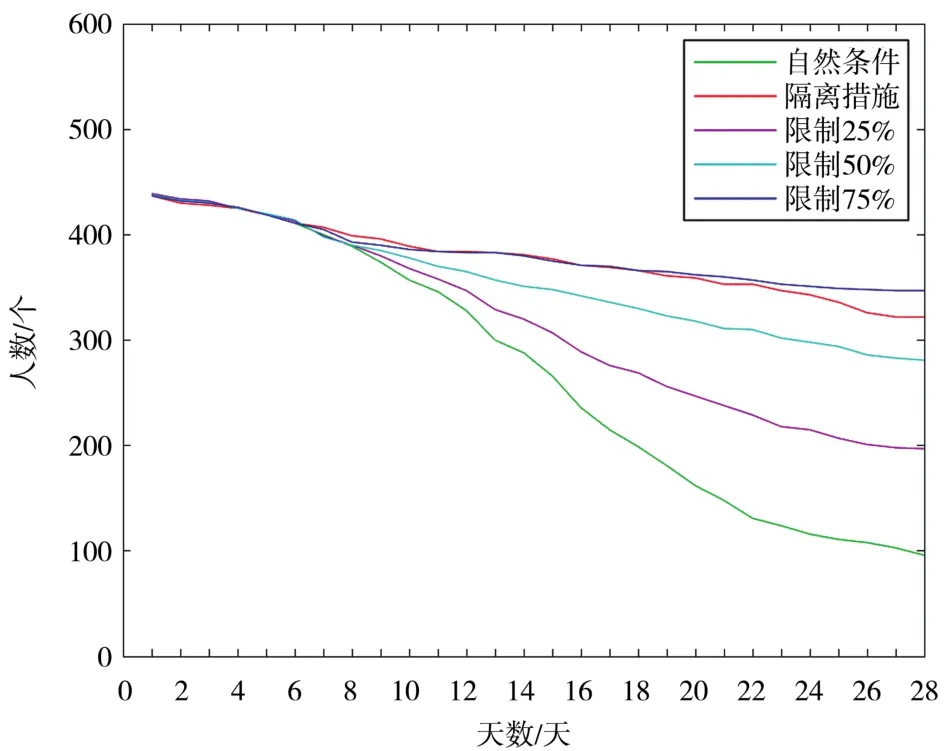
(1)在t=0时刻,将n(n< 图2 感染示意图 对于模型中的障碍物将按照以下步骤进行赋值,赋值结果如图3所示。 图3 布局图扫描赋值结果图(网格值×104) (1)确定场所出入口P(i,j),对出入口两侧元胞赋值为1,并按照离出口越远,值逐渐增加的规则进行赋值。 (2)若障碍物以单个网格形式出现,则值为1。 (3)由出入口P(i,j)两侧所在的行(或列)开始,对相邻的行(或列)进行扫描,对于墙壁的网格赋值为1,障碍物网格两端赋值为1,且由外向内逐渐增加。 本文基于经典场域模型[10-12],为使行人产生绕行的行为,现定义“视野距离”的概念:“视野距离”代表行人正前方的一段固定距离,将该固定距离记为dlim。 视野距离最远点(虚拟点)称为“决策点”,当决策点未“触碰”到障碍物时,行人会朝着目的地方向直线行走;当决策点“触碰”到障碍物时,如图4(a),行人的转向选择取决于决策点左前方和右前方网格值的大小,左前方网格值为5,大于右前方的网格值3,则行人将偏向右方行走,反之行人将偏向左方行走;当视野距离内的障碍物两端均为可绕行区域时,如图4(b)。当决策点(id,jd)左前方网格值和右前方网格值相等的时候,行人将会等概率选择往左、右转向。 图4 行人在不同位置处决策点情况 在绕行过程中,当决策点前方存在墙壁或障碍物时,决策点将会随着行人移动的方向跟着移动,且紧贴着墙壁或障碍物进行移动,来保证决策点与行人在同一直线上(如图4中决策点2′—3′过程)。而当行人成功绕过墙壁或障碍物时,决策点和行人的距离恢复到视野距离dlim。 行人根据其距各个目的地场所的欧氏距离和拥挤度两个因素进行选择。在前往目的地的过程中,行人将根据Moore型邻域空间的局部静态场值和局部动态场值进行移动[13-14]。 1.4.1 局部静态场 对于局部静态场而言,其计算公式依照以下两种情况: (1)当dlim=d时,行人的移动方向不受决策点的影响,保持着直线方向朝目标场所行走(图5),该情况下局部静态场计算式如下: 图5 决策点对行人无影响 (2)当dlim>d时,行人的移动方向将受到决策点的影响,此时行人将转向移动(图6),该情况下局部静态场S(i,j)计算式如下: 图6 决策点对行人产生影响 1.4.2 局部动态场计算公式 对于局部动态场而言,以行人在全局动态场中所处位置为中心的3×3矩阵值作为局部动态场值。根据经典场域模型理论,当(i,j)的元胞有行人经过时,则在下一时间步,该元胞动态场值D(i,j)=D(i,j)+1,其中,记扩散比例系数μ=0.1,衰减比例系数δ=0.2,当某一时刻元胞的动态场值D(i,j)≤ 0.1,则令D(i,j)= 0。 如图7所示,局部动态场取值于以行人在全局动态场中所处位置为中心的3×3矩阵值,为了与实际情况相结合,本模型不考虑行人后退移动的情况,从而行人的左后(右后)和正后方网格取值为0,基于该情况,计算式如下: 图7 局部动态场取值过程 其中,D(i,j)为矩阵在全局动态中所对应的位置;ND为局部动态场的归一化因子,计算表达式如下: 综合前面计算所得的局部静态场和动态场值,可以得到行人的3×3移动状态转移概率公式: 其中,kS为静态场敏感度参数;kD为动态场敏感度参数;ξ(i,j)表示元胞是否被行人所占据,有行人占据则值为0,反之取1;N为归一化因子,用来保证3×3状态转移矩阵概率之和为1,其计算表达式如下: 基于上述人员行走规则和传染病传播模式相互交叉迭代形成最终的元胞自动机系统,从而实现复杂密闭环境下传染病传播过程。现将建立的模型描述如下: (1)设置模型网络空间大小,出入口坐标集合和障碍物坐标集合。 (2)按照传染病传播演化规则模拟COVID-19传染病传播过程。 (3)按照式(10)计算得到行人移动状态转移概率矩阵,进行有目标的避让障碍物行走。当出现竞争同一网格时,将按照等概率原则随机选取一名个体进入目标网格。 (4)在以后的每一个离散时刻交叉迭代步骤(2)至步骤(3),模拟COVID-19在邮轮内部个体活动过程中的传播过程。 本文选取“钻石公主号”邮轮第5层甲板进行模拟仿真,该层的基本数据如表1所示。 表1 “钻石公主号”第5层甲板基本数据表 通过Netlogo编程平台[15-16],制作了可视化模拟器作为本模型的载体,包括呈现实时状态,实时调节可变参数,实时输出模拟数据等功能,如图8所示。 图8 可视化仿真图像 表2 仿真参数取值表 为了比较采取隔离措施对疫情防控的积极影响,借助本模型制作了SEI传染病模型下的仿真模拟。最大仿真天数设置为28天,其中,隔离措施下的隔离者被标记为灰色,并移动至邮轮环境外来保证仿真总人数不变且隔离者不对邮轮内部其他人员产生影响。 图9分别表示采取隔离措施时仿真时间为第 3、7、11、15、19和 25天的 COVID-19传播情况。图10分别表示未采取隔离措施时仿真时间为第3、7、11、15、19和25天的COVID-19传播情况。此外,本模型利用文献[2]给出的地铁站内COVID-19传染率参数进行仿真,参数取值如表3所示。 图9 COVID-19隔离条件下的演化过程 表3 传染率参数取值表 图10 COVID-19自然传播下的演化过程 图9—图10中的红色点代表感染者,黄色点代表潜伏者,绿色点代表健康者。通过图9和图10不同时刻的演化过程,发现自然传播条件下,邮轮内部的感染人群数量不断增加,而隔离措施下的感染者和潜伏者达到一定数量便维持恒定。 图11(a)中表示的是未隔离情况下,三种人群不同时刻状态曲线图,从11(a)中可以看出,潜伏者在中期达到了顶峰,健康者有一个下降最快的区间,过了这段区间后下降速率减缓,感染者相反,但通过趋势可以看出,健康者人数最终会趋于0,感染者人数将趋于总人数450。 图11 两种措施下人群感染状态趋势图 图11(b)表示的是隔离情况下,四种人群不同时刻状态曲线图,从图11(b)中可以看出,健康者人数不像图11(a),有一个下降最快的区间,而且潜伏者和感染者人数一直维持着一个较低的水平。但从曲线整体趋势来看,健康者依旧会被全部感染,但所需要的时间将远远大于图 11(a)所示情况。 两幅图对比之后可以看出,采取隔离措施能有效的减缓COVID-19传播速度,并抑制其进一步扩散,而未采取隔离措施时,COVID-19传播情况等同于自然状态下的SEI传播特征,随着后续仿真天数进一步延长,健康者均会被感染。 考虑当模拟过程中出现第一例感染者时,便限制行人出行,由原来的所有行人均可出行调整为75%、50%和25%的行人可以外出。 对比上述采取隔离措施情形,得到不同限制条件下的行人出行数量对疫情传播的影响,如图12所示。其中,曲线表示的是健康者随时间的数量变化。从图12看出,限制行人出行的防控效果十分有效,且随着限制力度的提高,即出行人数的下降,感染人数将得到有效的控制,图中当限制75%的行人出行时,对疫情的控制效果和隔离措施条件下的控制效果相当,且在后期显示出来的防控效果优于采取隔离措施条件。 图12 限制行人出行对疫情传播的影响 考虑人群对疫情的重视,采取一定的防护措施(例如戴口罩等)降低潜伏者和感染者传染健康人群的传染几率,此时对于这部分人群,传染率参数取值调整如表4所示。 表4 采取防护措施后传染率取值表 对比上述采取隔离措施情形,得到采取防护措施对疫情传播的影响如图13所示。从图13看出,采取个人防护措施在一定程度上能减缓COVID-19传播程度,但效果不如采取隔离措施好。 图13 防护措施对疫情传播的影响 通过上述数值实验结果可以看出,人口流动性会增大疫情的传播规模,因此当出现新冠肺炎疫情时,行人需要尽量降低外出的频率,此外,为了降低疫情在密闭复杂环境中的传播概率,需要采取个人防护措施,并且尽量远离人群。最后,在进行流行病调查时,一旦发现确诊的感染者,需要及时地采取隔离措施防止疫情继续的扩散。 本文将复杂密闭环境下的COVID-19传播模型通过人员行走与传染病传播交叉迭代的方式进行实现,较为真实地还原了邮轮内部人员日常出入场所的行为特征,符合现实情况。 从仿真结果可以看出,将元胞自动机理论借助Netlogo仿真工具去实现的方法适用于各类仿真模拟实验,既避免了传统的微分方程带来的复杂计算量,又客观有效地反映了疾病传播的动态过程,得到了是否采取隔离措施、是否采取防护措施以及限制不同出行人数对COVID-19传播的影响,通过模型的仿真结果得到,当疫情发生时,采取个人防护措施并减少外出是防范疫情的最佳策略。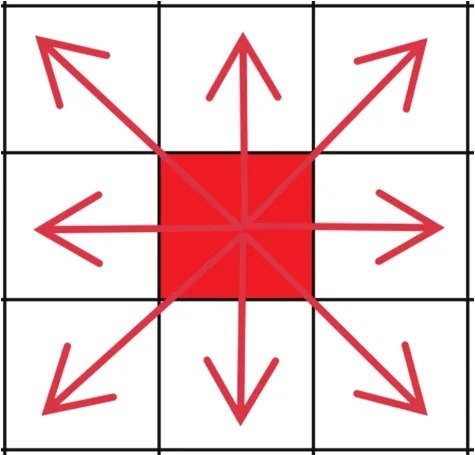
1.3 避让行走规则

1.4 移动规则
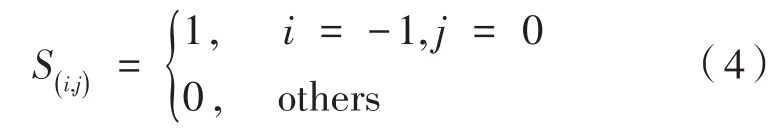

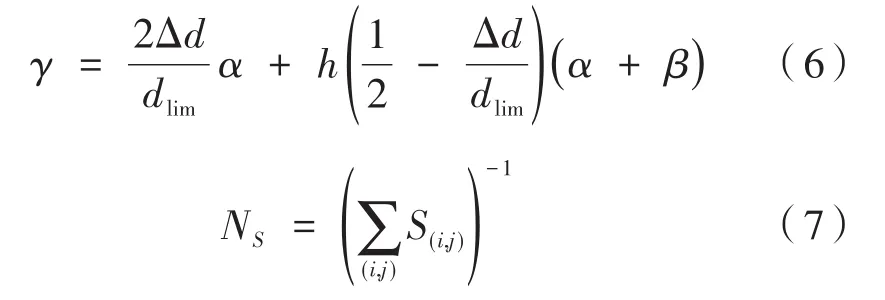
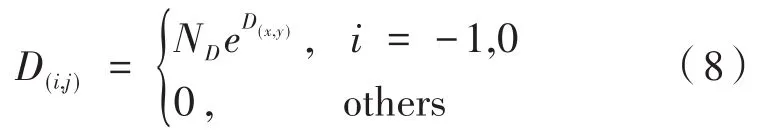
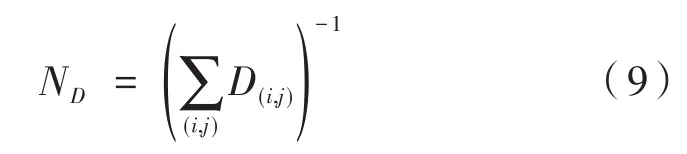
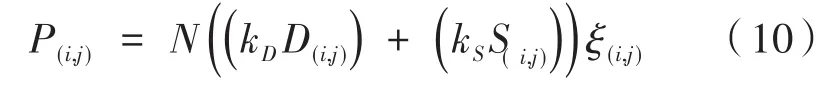

1.5 实验模型
2 以“钻石公主号”为例的实现
2.1 公主号邮轮
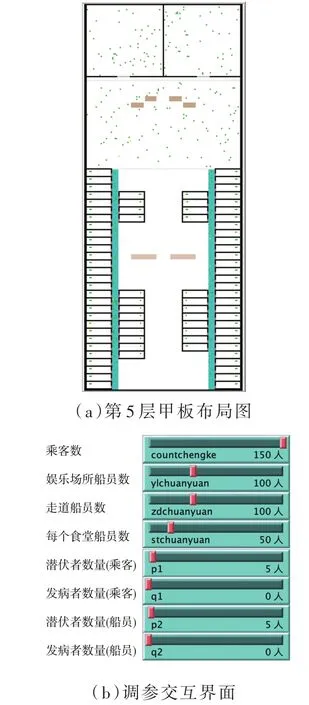
2.2 模型参数配置
2.3 隔离措施对疫情传播的影响
2.4 行人出行对疫情传播的影响
2.5 个人防护措施对疫情传播的影响


2.6 仿真结果分析
3 结论

